2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.1分类加法计数原理和分步乘法计数原理(第二课时)课件(共38张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.1分类加法计数原理和分步乘法计数原理(第二课时)课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 09:50:55 | ||
图片预览










文档简介
(共38张PPT)
分类加法计数原理和
分步乘法计数原理
(第二课时)
F佳
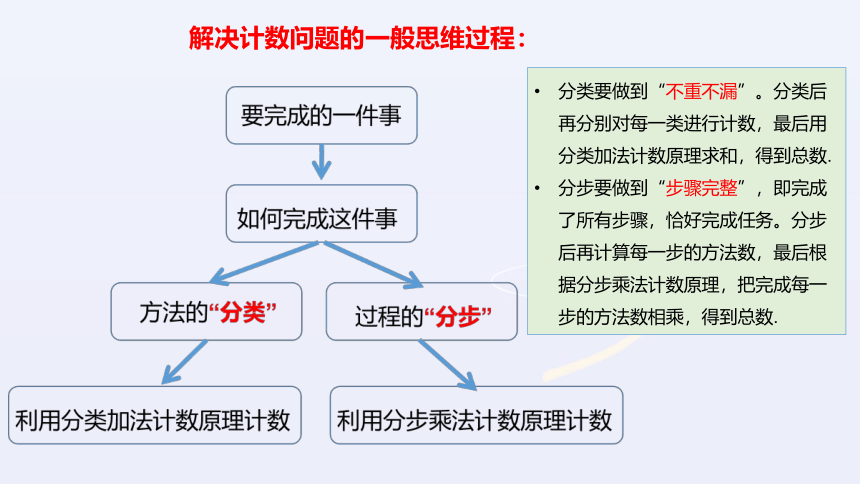
解决计数问题的一般思维过程:
分类要做到“不重不漏”。分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”,即完成了所有步骤,恰好完成任务。分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
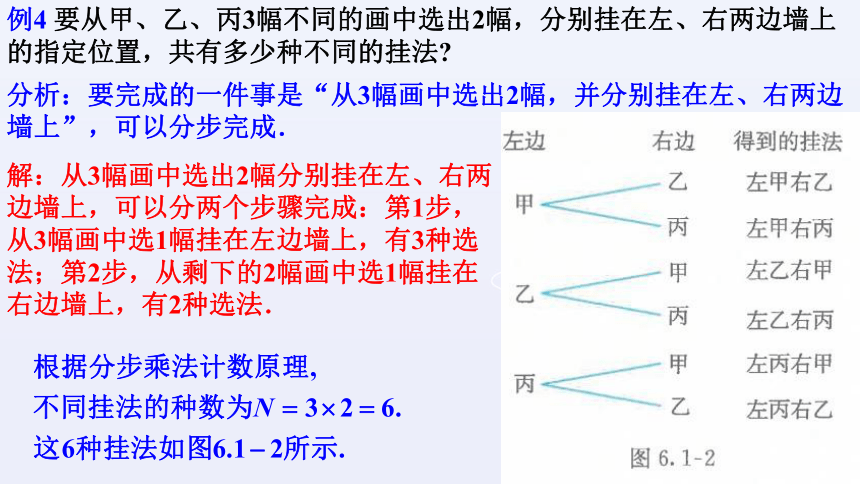
例4 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法
分析:要完成的一件事是“从3幅画中选出2幅,并分别挂在左、右两边墙上”,可以分步完成.
解:从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:第1步,从3幅画中选1幅挂在左边墙上,有3种选法;第2步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法.
例4改: 要从甲、乙、丙、丁4幅不同的画中选出3幅,分别挂在左、右、前三边墙上的指定位置,问共有多少种不同的挂法?
N=4 × 3 × 2=24
左边墙
右边墙
前面墙
3种
2种
4种
分析:要完成一件事是“给一个程序模块命名” ,可以分三个步骤完成:
第1步,首选字符,第2步,选中间字符;
第3步,选最后一个字符,还有首字符又可以分为两类。
例5.给程序模块命名,需要用3个字符,其中首字符要求用字母A~G或U~Z,后两个要求用数字1~9,问最多可以给多少个程序命名?
例6. 电子元件很容易实现电路的通与断、电位的高与低等两种状态,而这也是最容易控制的两种状态.因此计算机内部就采用了每一位只有0或1两种数字的记数法,即二进制.为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用一个或多个字节来表示,其中字节是计算机中数据存储的最小计量单位,每个字节由8个二进制位构成.问:
(1)一个字节(8位)最多可以表示多少个不同的字符?
(2)计算机汉字国际码(GB码)包含了6 763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
解:(1)用图6.1-3表示1个字节.
每个字符可以用一个或多个字节来表示,每个字节由8个二进制位构成.问:(1)一个字节(8位)最多可以表示多少个不同的字符?
(2)由(1)知,1个字节所能表示的不同字符不够6763个,我们考虑2个字节能够表示多少个字符.前1个字节有256种不同的表示方法,后1个字节也有256种表示方法.根据分步乘法计数原理,2个字节可以表示不同字符的个数是
这已经大于汉字国标码包含的汉字个数6763.因此要对这些汉字进行编码,每个汉字至少要用2个字节表示.
(2)计算机汉字国际码(GB码)包含了6 763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
课本P7 练习 1
1.某电话局管辖范围内的电话号码由8位数字组成,其中前4位的数字是不变的,后4位数字都是0~9之间的一个数字,这个电话局不同的电话号码最多有多少个
课本P7 练习 2
2.从5名同学中选出正、副组长各1名,有多少种不同的选法
课本P7 练习 3
3.从1,2,…,19,20中任选一个数作被减数,再从1,2,…,10中任选一个数作减数,然后写成一个减法算式,共可得到多少个不同的算式
课本P7 练习 5
5.由数字1,2,3,4,5可以组成多少个三位数(各位上的数字可以重复)
课本P7 练习 4
4.在1,2,…,500中,被5除余2的数共有多少个
用0,1,2,3,4五个数字,
(1)可以排成多少个三位数字的电话号码
(2)可以排成多少个三位数
(3)可以排成多少个能被2整除的无重复数字的三位数
例7. 计算机编程人员在编写好程序以后需要对程序进行测试,程序员需要知道到底有多少条执行路径(即程序从开始到结束的路线),以便知道需要提供多少个测试数据.一般地,一个程序模块由许多子模块组成.如图6.1-4所示是一个具有许多执行路径的程序模块.
(1)这个程序模块有多少条执行路径;
(2)为了减少测试时间,程序员需要设法减少测试次数,你能帮助程序员设计一个测试方法,以减少测试次数吗?
分析:整个模块,任意一条执行路径都分两步完成:第1步是从开始执行到A点,第2步是从A点执行到结束。而第1步可以由子模块1、2、3的任何一个完成,第2步可以由子模块4、5的任何一个完成。因此,分析一条命令在子模块中的执行路径需要用到两个计数原理。
图6.1-4
解答:(1)由分类加法计数原理可知,子模块1、2、3中子路径的条数共有:
18+45+28=91条
子模块4、5中子路径的条数共有:38+43=81条
又由分步乘法计数原理可知,整个模块的执行路径条数共有:
91×81=7371条
(2)在实际的测试中,程序员总是把每一个子模块看成一个黑箱,即通过只考察是否执行了正确的子模块的方式来测试整个模块。这样,他可以分别单独测试5个模块,以考察子模块的工作是否正常。需要测试的次数为:
18+45+28+38+43=172次
再测试各个模块之间信息交流是否正常,只需要测试第1步和第2步的各个子模块之间信息交流是否正常,需要测试的次数为:3×2=6次
总共需要测试172+6=178次
显然178与7371的差距是非常大的!
课本P11 练习 1
1.乘积(a1+a2+a3)(b1+b2+b3)(c1+c2+c3+c4+c5)展开后共有多少项
课本P11 练习 3
3.某商场有6个门,如果某人从其中的任意一个门进入商场,并且要求从其他的门出去,那么共有多少种不同的进出商场的方式
课本P11 习题6.1 3
3.如图,要让电路从A处到B处只有一条支路接通,可有多少条不同的路径
课本P11 习题6.1 6
6.(1)在平面直角坐标系内,横坐标与纵坐标均在A={0,1,2,3,4,5}内取值的不同点共有多少个
(2)在平面直角坐标系内,斜率在集合 B={1,3,5,7}内取值,y轴上的截距在集合C={2,4,6,8}内取值的不同直线共有多少条
课本P12 习题6.1 7
7.一种号码锁有4个拨号盘,每个拨号盘上有0~9共10个数字.现最后一个拨号盘出现了故障,只能在0~5这6个数字中拨号,这4个拨号盘可组成多少个四位数字号码
课本P12 习题6.1 8
8.(1)4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,不同报法的种数是34还是43
(2)3个班分别从5个景点中选择一处游览,不同选法的种数是35 还是53
课本P12 习题6.1 9
9.(1)从5件不同的礼物中选出4件送给4位同学,每人一件,有多少种不同的送法
(2)有5个编了号的抽屉,要放进3本不同的书,不同的放法有多少种 (一个抽屉可放多本书.)
课本P12 习题6.1 11
11.在国庆长假期间,要从7人中选若干人在7天假期值班(每天只需1人值班),不出现同一人连续值班2天,有多少种可能的安排方法
有A,B两种类型的车床各一台,现有甲、乙、丙三名工人,其中甲、乙都会操作两种车床,丙只会操作 A种车床,要从这三名工人中选两名分别去操作这两种车床,则不同的选派方法有( )
A.6种 B.5种 C.4种 D.3种
某班有3名学生准备参加校运会的100米、200米、跳高、跳远四项比赛,如果每班每项限报1人,则这3名学生的参赛的不同方法有( )
A.24种 B.48种 C.64种 D.81种
火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有
A.510种 发B.105种 C.50种 D.500种
例8. 通常,我国民用汽车号牌的编号由两部分组成:第一部分为用汉字表示的省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图所示.
其中,序号的编码规则为:
(1)由10个阿拉伯数字和除O,
I之外的24个英文字母组成;
(2)最多只能有2个英文字母.
如果某地级市发牌机关采用5位序号编码,那么这个发牌机关最多
能发放多少张汽车号牌?
分析:由号牌编号的组成可知,序号的个数决定了这个发牌机关所能发放的最多号牌数,按程序编码规则可知,每个序号中的数字、字母都是可重复的,并且可将序号分为三类;没有字母,有1个字母,有2个字母,以字母所在位置为分类标准,可将有1个字母的序号,分为五个子类,将有2个字母的序号,分为十个子类.
解:根据序号编码规则,5位序号可以分为三类:
没有字母,有1个字母,有2个字母.
(1)当没有字母时,确定一个序号可分5个步骤,每一步都有10个选择, 根据分布乘法计数原理,这类号牌张数为
10×10×10×10×10=100000.
②同理,其余四个子类号牌也各有240000张.
根据分类加法计数原理,这类号牌张数,共为
240000+240000+240000+240000+240000=1200000.
第2~5步都有10种选法,
根据分步乘法计数原理,号牌张数为:24×10×10×10×10=240000.
①当第1位是字母时,分5步确定:
第1步,从24个字母中选1个放在第1位,有24种选法;
(2)当有1个字母时,按字母位置,这类序号可以分为五个子类.
(3) 有2个字母时,由2个字母在序号中的位置,可分为十个子类:
第1位和第2位,第1位和第3位,第1位和第4位,第1位和第5位,……第4位和第5位.
①第1位和第2位为字母时,确定一个分5步:
第1~2步都是从24个字母中选1个分别放在第1位,第2位,各有24种选法;
第3~5步都是从10个数字中选1个放在相应的位置,各有10种选法.
根据分步乘法计数原理,号牌张数为24×24×10×10×10=576000
同理另外九个子类号牌也有576000张这类号牌张数一共576000×10=5760000
综合上述,由分类加法计数原理,这个发牌机关最多能发放的汽车号牌张数为10000十1200000+5760000=7060000.
高三年级的三个班到甲、乙、丙、丁四个工厂进行社会实践,其中工厂甲必须有班级去,每班去何工厂可自由选择,则不同的分配方案有( )
A.16种 B.18种 C.37种 D.48种
如图,用4种不同的颜色涂入图中的矩形 A,B,C,D中,要求相邻的矩形涂色不同,则不同的涂法有____________种。
时间:运动会前三个月
事件:体育委员要求参赛的5名长跑运动员每天训练一次。其中有几名运动员商议要休息几天。
体育委员说:“以后每天训练由我给你们排队集合,如果哪天我排的队和前面哪一次完全重复了,那以后就不用训练了。”
5名运动员排队有几种不同的排法?
解密约定
5 × 4 × 3 × 2 × 1=120
本小节结束
F佳
分类加法计数原理和
分步乘法计数原理
(第二课时)
F佳
解决计数问题的一般思维过程:
分类要做到“不重不漏”。分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”,即完成了所有步骤,恰好完成任务。分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
例4 要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法
分析:要完成的一件事是“从3幅画中选出2幅,并分别挂在左、右两边墙上”,可以分步完成.
解:从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:第1步,从3幅画中选1幅挂在左边墙上,有3种选法;第2步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法.
例4改: 要从甲、乙、丙、丁4幅不同的画中选出3幅,分别挂在左、右、前三边墙上的指定位置,问共有多少种不同的挂法?
N=4 × 3 × 2=24
左边墙
右边墙
前面墙
3种
2种
4种
分析:要完成一件事是“给一个程序模块命名” ,可以分三个步骤完成:
第1步,首选字符,第2步,选中间字符;
第3步,选最后一个字符,还有首字符又可以分为两类。
例5.给程序模块命名,需要用3个字符,其中首字符要求用字母A~G或U~Z,后两个要求用数字1~9,问最多可以给多少个程序命名?
例6. 电子元件很容易实现电路的通与断、电位的高与低等两种状态,而这也是最容易控制的两种状态.因此计算机内部就采用了每一位只有0或1两种数字的记数法,即二进制.为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用一个或多个字节来表示,其中字节是计算机中数据存储的最小计量单位,每个字节由8个二进制位构成.问:
(1)一个字节(8位)最多可以表示多少个不同的字符?
(2)计算机汉字国际码(GB码)包含了6 763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
解:(1)用图6.1-3表示1个字节.
每个字符可以用一个或多个字节来表示,每个字节由8个二进制位构成.问:(1)一个字节(8位)最多可以表示多少个不同的字符?
(2)由(1)知,1个字节所能表示的不同字符不够6763个,我们考虑2个字节能够表示多少个字符.前1个字节有256种不同的表示方法,后1个字节也有256种表示方法.根据分步乘法计数原理,2个字节可以表示不同字符的个数是
这已经大于汉字国标码包含的汉字个数6763.因此要对这些汉字进行编码,每个汉字至少要用2个字节表示.
(2)计算机汉字国际码(GB码)包含了6 763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
课本P7 练习 1
1.某电话局管辖范围内的电话号码由8位数字组成,其中前4位的数字是不变的,后4位数字都是0~9之间的一个数字,这个电话局不同的电话号码最多有多少个
课本P7 练习 2
2.从5名同学中选出正、副组长各1名,有多少种不同的选法
课本P7 练习 3
3.从1,2,…,19,20中任选一个数作被减数,再从1,2,…,10中任选一个数作减数,然后写成一个减法算式,共可得到多少个不同的算式
课本P7 练习 5
5.由数字1,2,3,4,5可以组成多少个三位数(各位上的数字可以重复)
课本P7 练习 4
4.在1,2,…,500中,被5除余2的数共有多少个
用0,1,2,3,4五个数字,
(1)可以排成多少个三位数字的电话号码
(2)可以排成多少个三位数
(3)可以排成多少个能被2整除的无重复数字的三位数
例7. 计算机编程人员在编写好程序以后需要对程序进行测试,程序员需要知道到底有多少条执行路径(即程序从开始到结束的路线),以便知道需要提供多少个测试数据.一般地,一个程序模块由许多子模块组成.如图6.1-4所示是一个具有许多执行路径的程序模块.
(1)这个程序模块有多少条执行路径;
(2)为了减少测试时间,程序员需要设法减少测试次数,你能帮助程序员设计一个测试方法,以减少测试次数吗?
分析:整个模块,任意一条执行路径都分两步完成:第1步是从开始执行到A点,第2步是从A点执行到结束。而第1步可以由子模块1、2、3的任何一个完成,第2步可以由子模块4、5的任何一个完成。因此,分析一条命令在子模块中的执行路径需要用到两个计数原理。
图6.1-4
解答:(1)由分类加法计数原理可知,子模块1、2、3中子路径的条数共有:
18+45+28=91条
子模块4、5中子路径的条数共有:38+43=81条
又由分步乘法计数原理可知,整个模块的执行路径条数共有:
91×81=7371条
(2)在实际的测试中,程序员总是把每一个子模块看成一个黑箱,即通过只考察是否执行了正确的子模块的方式来测试整个模块。这样,他可以分别单独测试5个模块,以考察子模块的工作是否正常。需要测试的次数为:
18+45+28+38+43=172次
再测试各个模块之间信息交流是否正常,只需要测试第1步和第2步的各个子模块之间信息交流是否正常,需要测试的次数为:3×2=6次
总共需要测试172+6=178次
显然178与7371的差距是非常大的!
课本P11 练习 1
1.乘积(a1+a2+a3)(b1+b2+b3)(c1+c2+c3+c4+c5)展开后共有多少项
课本P11 练习 3
3.某商场有6个门,如果某人从其中的任意一个门进入商场,并且要求从其他的门出去,那么共有多少种不同的进出商场的方式
课本P11 习题6.1 3
3.如图,要让电路从A处到B处只有一条支路接通,可有多少条不同的路径
课本P11 习题6.1 6
6.(1)在平面直角坐标系内,横坐标与纵坐标均在A={0,1,2,3,4,5}内取值的不同点共有多少个
(2)在平面直角坐标系内,斜率在集合 B={1,3,5,7}内取值,y轴上的截距在集合C={2,4,6,8}内取值的不同直线共有多少条
课本P12 习题6.1 7
7.一种号码锁有4个拨号盘,每个拨号盘上有0~9共10个数字.现最后一个拨号盘出现了故障,只能在0~5这6个数字中拨号,这4个拨号盘可组成多少个四位数字号码
课本P12 习题6.1 8
8.(1)4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,不同报法的种数是34还是43
(2)3个班分别从5个景点中选择一处游览,不同选法的种数是35 还是53
课本P12 习题6.1 9
9.(1)从5件不同的礼物中选出4件送给4位同学,每人一件,有多少种不同的送法
(2)有5个编了号的抽屉,要放进3本不同的书,不同的放法有多少种 (一个抽屉可放多本书.)
课本P12 习题6.1 11
11.在国庆长假期间,要从7人中选若干人在7天假期值班(每天只需1人值班),不出现同一人连续值班2天,有多少种可能的安排方法
有A,B两种类型的车床各一台,现有甲、乙、丙三名工人,其中甲、乙都会操作两种车床,丙只会操作 A种车床,要从这三名工人中选两名分别去操作这两种车床,则不同的选派方法有( )
A.6种 B.5种 C.4种 D.3种
某班有3名学生准备参加校运会的100米、200米、跳高、跳远四项比赛,如果每班每项限报1人,则这3名学生的参赛的不同方法有( )
A.24种 B.48种 C.64种 D.81种
火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有
A.510种 发B.105种 C.50种 D.500种
例8. 通常,我国民用汽车号牌的编号由两部分组成:第一部分为用汉字表示的省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图所示.
其中,序号的编码规则为:
(1)由10个阿拉伯数字和除O,
I之外的24个英文字母组成;
(2)最多只能有2个英文字母.
如果某地级市发牌机关采用5位序号编码,那么这个发牌机关最多
能发放多少张汽车号牌?
分析:由号牌编号的组成可知,序号的个数决定了这个发牌机关所能发放的最多号牌数,按程序编码规则可知,每个序号中的数字、字母都是可重复的,并且可将序号分为三类;没有字母,有1个字母,有2个字母,以字母所在位置为分类标准,可将有1个字母的序号,分为五个子类,将有2个字母的序号,分为十个子类.
解:根据序号编码规则,5位序号可以分为三类:
没有字母,有1个字母,有2个字母.
(1)当没有字母时,确定一个序号可分5个步骤,每一步都有10个选择, 根据分布乘法计数原理,这类号牌张数为
10×10×10×10×10=100000.
②同理,其余四个子类号牌也各有240000张.
根据分类加法计数原理,这类号牌张数,共为
240000+240000+240000+240000+240000=1200000.
第2~5步都有10种选法,
根据分步乘法计数原理,号牌张数为:24×10×10×10×10=240000.
①当第1位是字母时,分5步确定:
第1步,从24个字母中选1个放在第1位,有24种选法;
(2)当有1个字母时,按字母位置,这类序号可以分为五个子类.
(3) 有2个字母时,由2个字母在序号中的位置,可分为十个子类:
第1位和第2位,第1位和第3位,第1位和第4位,第1位和第5位,……第4位和第5位.
①第1位和第2位为字母时,确定一个分5步:
第1~2步都是从24个字母中选1个分别放在第1位,第2位,各有24种选法;
第3~5步都是从10个数字中选1个放在相应的位置,各有10种选法.
根据分步乘法计数原理,号牌张数为24×24×10×10×10=576000
同理另外九个子类号牌也有576000张这类号牌张数一共576000×10=5760000
综合上述,由分类加法计数原理,这个发牌机关最多能发放的汽车号牌张数为10000十1200000+5760000=7060000.
高三年级的三个班到甲、乙、丙、丁四个工厂进行社会实践,其中工厂甲必须有班级去,每班去何工厂可自由选择,则不同的分配方案有( )
A.16种 B.18种 C.37种 D.48种
如图,用4种不同的颜色涂入图中的矩形 A,B,C,D中,要求相邻的矩形涂色不同,则不同的涂法有____________种。
时间:运动会前三个月
事件:体育委员要求参赛的5名长跑运动员每天训练一次。其中有几名运动员商议要休息几天。
体育委员说:“以后每天训练由我给你们排队集合,如果哪天我排的队和前面哪一次完全重复了,那以后就不用训练了。”
5名运动员排队有几种不同的排法?
解密约定
5 × 4 × 3 × 2 × 1=120
本小节结束
F佳
