北师大版七年级数学下册 2.3 平行线的性质 课件(共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 2.3 平行线的性质 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 481.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 16:15:40 | ||
图片预览





文档简介
(共23张PPT)
平行线的性质
北师大版七年级下册数学
学习目标:
1、探索平行线的性质;
2、会用平行线的性质进行简单的计算与说理;
3、了解平行线的性质和判定的区别。
重 点:
1、探究、归纳平行线的性质;
2、区分平行线的性质与判定。
难 点:
1、平行线的性质定理的推导;
2、能用平行线的性质进行简单的计算与说理。
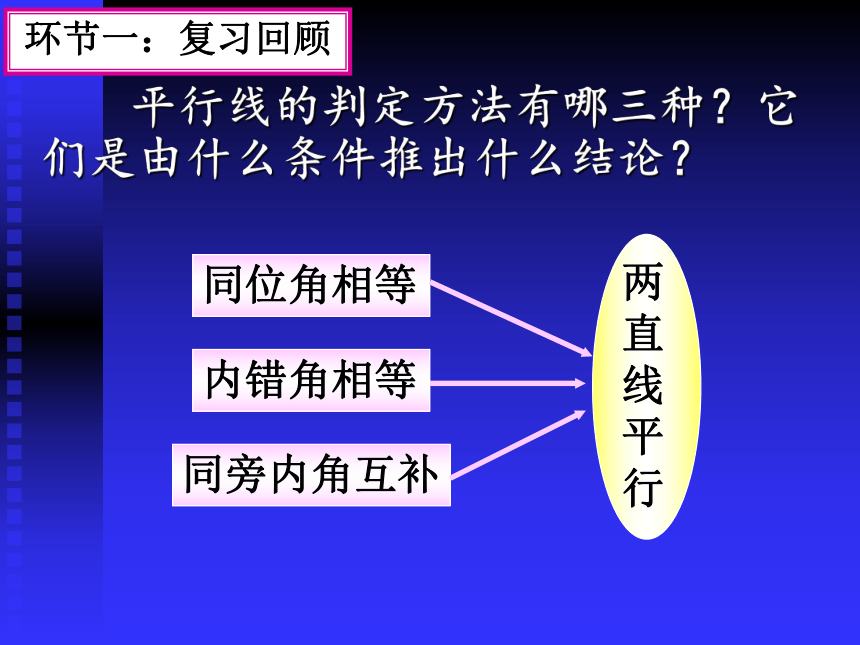
平行线的判定方法有哪三种?它们是由什么条件推出什么结论?
环节一:复习回顾
同位角相等
内错角相等
同旁内角互补
两直线平行
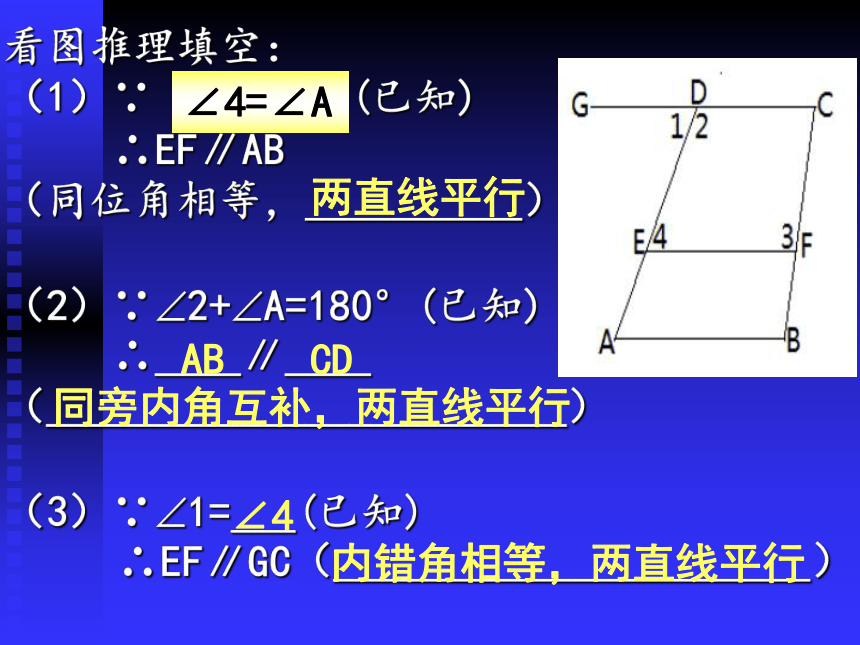
看图推理填空:
(1)∵ _______ (已知)
∴EF∥AB
(同位角相等,__________)
(2)∵ 2+ A=180°(已知)
∴____∥____
(________________________)
(3)∵ 1=___(已知)
∴EF∥GC(______________________)
两直线平行
AB
CD
同旁内角互补,两直线平行
∠3=∠B
∠4
内错角相等,两直线平行
∠4=∠A
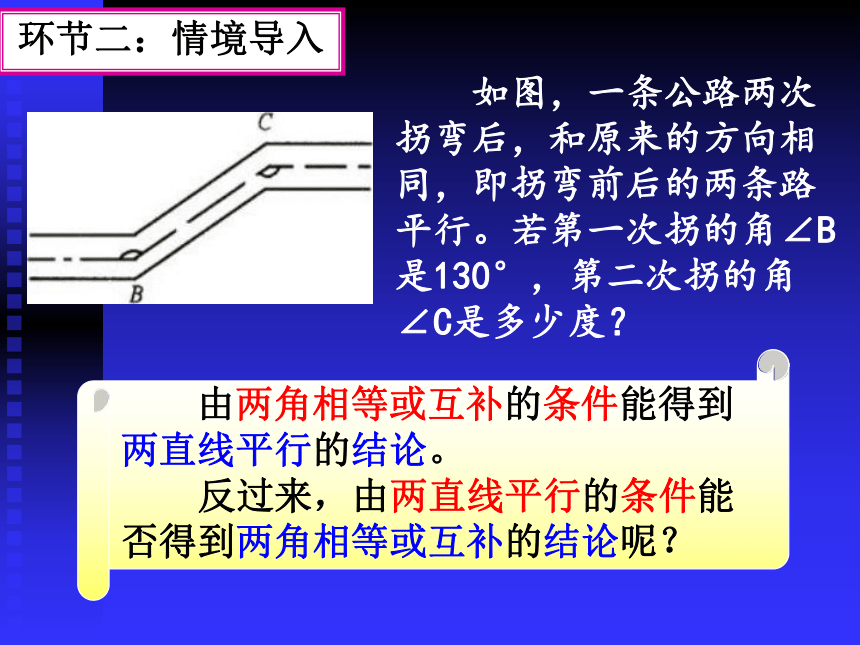
如图,一条公路两次拐弯后,和原来的方向相同,即拐弯前后的两条路平行。若第一次拐的角∠B 是130°,第二次拐的角∠C是多少度?
环节二:情境导入
由两角相等或互补的条件能得到两直线平行的结论。
反过来,由两直线平行的条件能否得到两角相等或互补的结论呢?
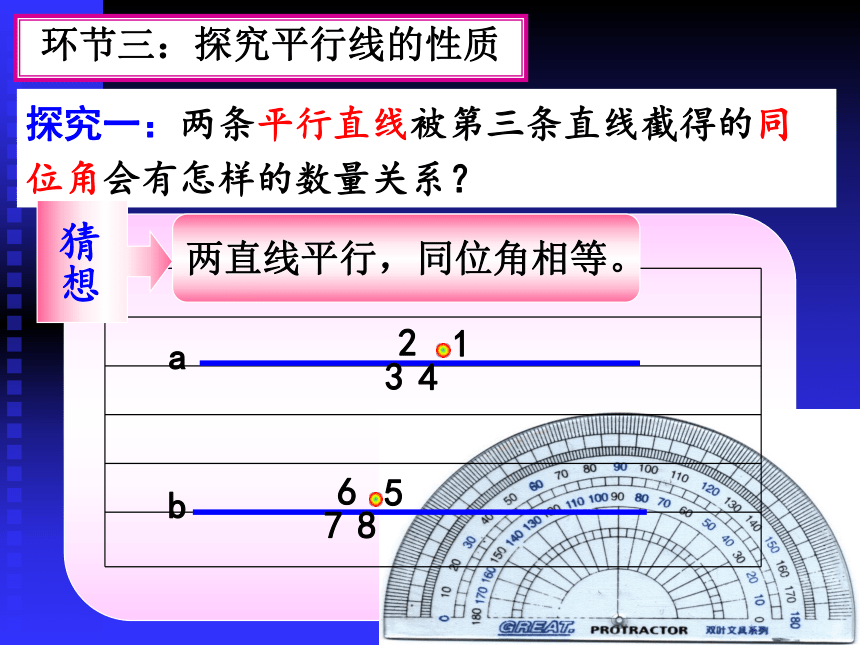
环节三:探究平行线的性质
探究一:两条平行直线被第三条直线截得的同位角会有怎样的数量关系?
a
b
c
猜想
两直线平行,同位角相等。
1
5
2
4
3
7
8
6
证明:(反证法)假设∠1≠∠2,则过∠1顶点O作直线A1B1,使∠EOB1=∠2。
∵∠EOB1=∠2(已作)
∴A1B1∥___(______________________)
又∵AB∥CD
∴过O点有__条直线与已知直线CD平行,
这与____公理矛盾.
即假设∠1≠∠2______(填“正确”
或“不正确).
∴∠1__∠2.
推理验证猜想
已知:直线AB、CD被EF所截,
直线EF与AB交于点O,AB∥CD。
求证:∠1=∠2。
CD
同位角相等,两直线平行。
两
平行
不正确
=
平行线的性质1
两条平行直线被第三条直线所截,同位
角相等。
简称为:两直线平行,同位角相等。
几何符号语言:
∵a∥b
∴∠1=∠5
环节三:探究平行线的性质
探究二:两条平行直线被第三条直线截得的内错角会有怎样的数量关系?
a
b
c
猜想
两直线平行,内错角相等。
3
1
2
4
8
5
6
7
推理验证猜想
答:已知a//b,那么________。
理由:∵a∥b(已知)
∴∠1=∠___
(_______________________) 又∵∠1=∠___(对顶角相等)
∴_________(等量代换)
如图,已知a//b,那么 2与 3
有什么数量关系?(请利用“平行
线的性质1”说明理由)
∠2=∠3
2
两直线平行,同位角相等。
3
∠2=∠3
平行线的性质2
两条平行直线被第三条直线所截,内错
角相等。
简称为:两直线平行,内错角相等。
几何符号语言:
∵a∥b
∴∠3=∠6
环节三:探究平行线的性质
探究三:两条平行直线被第三条直线截得的同旁内角会有怎样的数量关系?
a
b
c
猜想
两直线平行,同旁内角互补。
4
1
2
3
5
6
7
8
推理验证猜想
如图,已知a//b,那么 2与 3
有什么数量关系?(请利用“平行
线的性质1”说明理由)
答:已知a//b,那么__________。
理由:
∵a∥b(已知)
∴∠1=∠3(两直线平行,同位角相等。)
又∵∠1+∠2=180°(邻补角定义)
∴ ∠2+∠3=180°(等量代换)
∠2+∠3=180°
平行线的性质3
两条平行直线被第三条直线所截,同旁内
角互补。
简称为:两直线平行,同旁内角互补。
几何符号语言:
∵a∥b
∴∠3+∠5=180°
环节四:对比分析,深化理解
思考1:如果两条不平行的直线被第三条直线所截,同位角相等吗?内错角相等吗?同旁内角互补吗?
思考2:你如何区分平行线的性质与判定?
条件
判定
结论
条件
性质
结论
同位角相等
内错角相等
同旁内角互补
两
直
线
平
行
两
直
线
平
行
同位角相等
内错角相等
同旁内角互补
环节五:巩固新知,强化运用
1、如图,一条公路两次拐弯后,和原来的方向相同,即拐弯前后的两条路平行。若第一次拐的角∠B 是130°,第二次拐的角∠C是多少度?
2、如图所示,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4。
(1)∠1和∠3的大小有什么关系?∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
环节五:巩固新知,强化运用
解:(1)∵AB∥DE(已知)
∴∠1=∠3( ____)
又∵∠1=∠2(已知)
∴∠2= (等量代换)
又∵∠3=∠4(____)
∴∠2= (_________)
(2)∵∠2=∠4(已证)
∴BC___EF( ___)
思考:题中的这两问用到的分别是平行线的性质还是判定?
两直线平行,同位角相等。
∠3
已知
∠4
等量代换
∥
同位角相等,两直线平行。
3、如图,AB∥CD,AD平分∠CAD,
∠C=110°,求∠DAB的度数。
解:∵AB∥CD (已知)
∴∠C+∠CAB=180°(两直线平行,同旁内角互补)
又∵∠C=110°(已知)
∴∠CAB=70°
∵ AD平分∠CAD(已知)
∴∠DAB=1/2∠CAB=35°(角平分线定义)
环节五:巩固新知,强化运用
(1)如图1,AB∥CD,
试说明:∠B+∠D=∠BED.
(2)如图2,AB∥CD,
试说明:∠B+∠BED+∠D=360°.
图1
图2
方法总结:平行线中的拐点问题,通常需
过拐点作平行线.
F
1
2
F
1
2
环节六:拓展提升
环节七:归纳总结
1、平行线的性质是什么?
2、平行线的性质的作用是什么?
平行线的性质
北师大版七年级下册数学
学习目标:
1、探索平行线的性质;
2、会用平行线的性质进行简单的计算与说理;
3、了解平行线的性质和判定的区别。
重 点:
1、探究、归纳平行线的性质;
2、区分平行线的性质与判定。
难 点:
1、平行线的性质定理的推导;
2、能用平行线的性质进行简单的计算与说理。
平行线的判定方法有哪三种?它们是由什么条件推出什么结论?
环节一:复习回顾
同位角相等
内错角相等
同旁内角互补
两直线平行
看图推理填空:
(1)∵ _______ (已知)
∴EF∥AB
(同位角相等,__________)
(2)∵ 2+ A=180°(已知)
∴____∥____
(________________________)
(3)∵ 1=___(已知)
∴EF∥GC(______________________)
两直线平行
AB
CD
同旁内角互补,两直线平行
∠3=∠B
∠4
内错角相等,两直线平行
∠4=∠A
如图,一条公路两次拐弯后,和原来的方向相同,即拐弯前后的两条路平行。若第一次拐的角∠B 是130°,第二次拐的角∠C是多少度?
环节二:情境导入
由两角相等或互补的条件能得到两直线平行的结论。
反过来,由两直线平行的条件能否得到两角相等或互补的结论呢?
环节三:探究平行线的性质
探究一:两条平行直线被第三条直线截得的同位角会有怎样的数量关系?
a
b
c
猜想
两直线平行,同位角相等。
1
5
2
4
3
7
8
6
证明:(反证法)假设∠1≠∠2,则过∠1顶点O作直线A1B1,使∠EOB1=∠2。
∵∠EOB1=∠2(已作)
∴A1B1∥___(______________________)
又∵AB∥CD
∴过O点有__条直线与已知直线CD平行,
这与____公理矛盾.
即假设∠1≠∠2______(填“正确”
或“不正确).
∴∠1__∠2.
推理验证猜想
已知:直线AB、CD被EF所截,
直线EF与AB交于点O,AB∥CD。
求证:∠1=∠2。
CD
同位角相等,两直线平行。
两
平行
不正确
=
平行线的性质1
两条平行直线被第三条直线所截,同位
角相等。
简称为:两直线平行,同位角相等。
几何符号语言:
∵a∥b
∴∠1=∠5
环节三:探究平行线的性质
探究二:两条平行直线被第三条直线截得的内错角会有怎样的数量关系?
a
b
c
猜想
两直线平行,内错角相等。
3
1
2
4
8
5
6
7
推理验证猜想
答:已知a//b,那么________。
理由:∵a∥b(已知)
∴∠1=∠___
(_______________________) 又∵∠1=∠___(对顶角相等)
∴_________(等量代换)
如图,已知a//b,那么 2与 3
有什么数量关系?(请利用“平行
线的性质1”说明理由)
∠2=∠3
2
两直线平行,同位角相等。
3
∠2=∠3
平行线的性质2
两条平行直线被第三条直线所截,内错
角相等。
简称为:两直线平行,内错角相等。
几何符号语言:
∵a∥b
∴∠3=∠6
环节三:探究平行线的性质
探究三:两条平行直线被第三条直线截得的同旁内角会有怎样的数量关系?
a
b
c
猜想
两直线平行,同旁内角互补。
4
1
2
3
5
6
7
8
推理验证猜想
如图,已知a//b,那么 2与 3
有什么数量关系?(请利用“平行
线的性质1”说明理由)
答:已知a//b,那么__________。
理由:
∵a∥b(已知)
∴∠1=∠3(两直线平行,同位角相等。)
又∵∠1+∠2=180°(邻补角定义)
∴ ∠2+∠3=180°(等量代换)
∠2+∠3=180°
平行线的性质3
两条平行直线被第三条直线所截,同旁内
角互补。
简称为:两直线平行,同旁内角互补。
几何符号语言:
∵a∥b
∴∠3+∠5=180°
环节四:对比分析,深化理解
思考1:如果两条不平行的直线被第三条直线所截,同位角相等吗?内错角相等吗?同旁内角互补吗?
思考2:你如何区分平行线的性质与判定?
条件
判定
结论
条件
性质
结论
同位角相等
内错角相等
同旁内角互补
两
直
线
平
行
两
直
线
平
行
同位角相等
内错角相等
同旁内角互补
环节五:巩固新知,强化运用
1、如图,一条公路两次拐弯后,和原来的方向相同,即拐弯前后的两条路平行。若第一次拐的角∠B 是130°,第二次拐的角∠C是多少度?
2、如图所示,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4。
(1)∠1和∠3的大小有什么关系?∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
环节五:巩固新知,强化运用
解:(1)∵AB∥DE(已知)
∴∠1=∠3( ____)
又∵∠1=∠2(已知)
∴∠2= (等量代换)
又∵∠3=∠4(____)
∴∠2= (_________)
(2)∵∠2=∠4(已证)
∴BC___EF( ___)
思考:题中的这两问用到的分别是平行线的性质还是判定?
两直线平行,同位角相等。
∠3
已知
∠4
等量代换
∥
同位角相等,两直线平行。
3、如图,AB∥CD,AD平分∠CAD,
∠C=110°,求∠DAB的度数。
解:∵AB∥CD (已知)
∴∠C+∠CAB=180°(两直线平行,同旁内角互补)
又∵∠C=110°(已知)
∴∠CAB=70°
∵ AD平分∠CAD(已知)
∴∠DAB=1/2∠CAB=35°(角平分线定义)
环节五:巩固新知,强化运用
(1)如图1,AB∥CD,
试说明:∠B+∠D=∠BED.
(2)如图2,AB∥CD,
试说明:∠B+∠BED+∠D=360°.
图1
图2
方法总结:平行线中的拐点问题,通常需
过拐点作平行线.
F
1
2
F
1
2
环节六:拓展提升
环节七:归纳总结
1、平行线的性质是什么?
2、平行线的性质的作用是什么?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
