青岛版(五四制)数学五年级下册 第五单元第1课《比例的认识》 课件(共30张PPT)
文档属性
| 名称 | 青岛版(五四制)数学五年级下册 第五单元第1课《比例的认识》 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 702.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 09:01:45 | ||
图片预览










文档简介
(共30张PPT)
第5单元啤酒生产中的数学
1.比例的意义和基本性质
学习目标
●理解比例的意义和基本性质。掌握比例各部分的名称,能正确读写、比例。
●理解并掌握比例的基本性质,会判断两个比能否组成比例。
●通过自主学习,经历探究的过程,体验数学学习的快乐,培养学生负责、团结合作的精神。
复习导入
什么叫作比?
什么叫作比值?
两个数相除,叫作两个数的比。
比的前项除以后项的商,叫作比值。
复习导入
求下列各比的比值。
4.5:9
12:16
6:1.5
情景导入
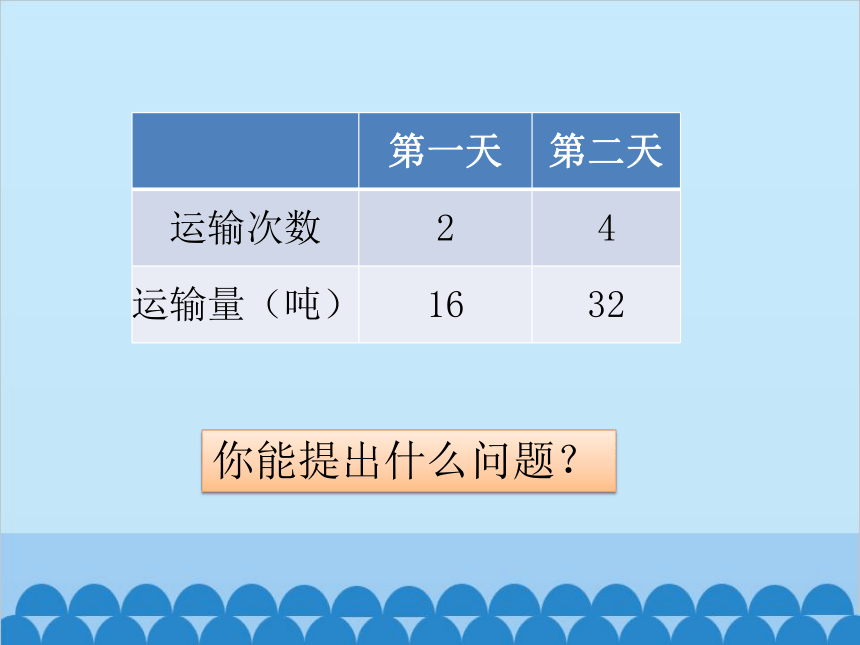
第一天 第二天
运输次数 2 4
运输量(吨) 16 32
第一天 第二天
运输次数 2 4
运输量(吨) 16 32
你能提出什么问题?
合作探究
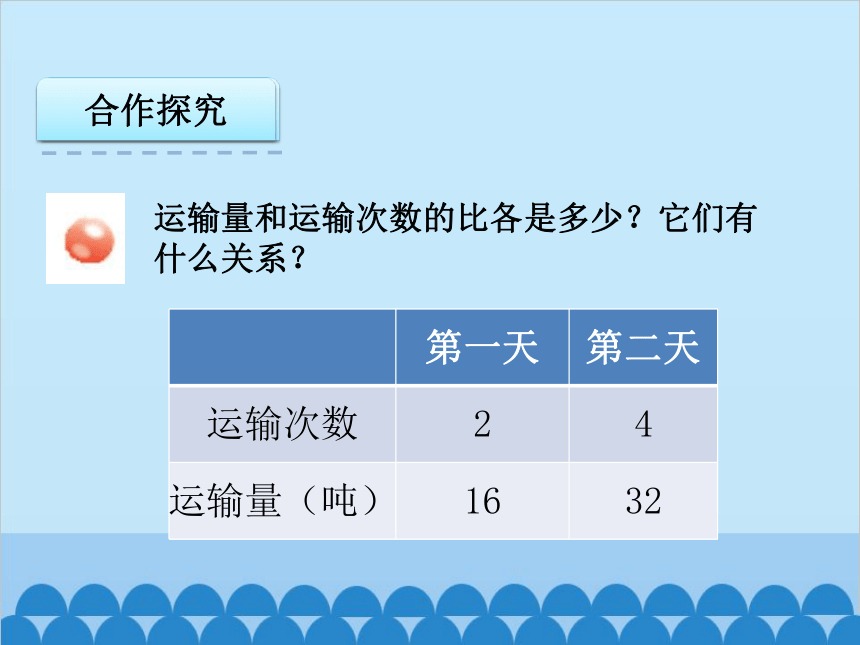
运输量和运输次数的比各是多少?它们有什么关系?
第一天 第二天
运输次数 2 4
运输量(吨) 16 32
第一天运输量和运输次数的比是:
16 :2
第二天运输量和运输次数的比是:
32 :4
我发现运输量和运输次的比数的比值相等。
16 :2=8
32 :4=8
两个比相等,可以写成下面的式子:
16 :2=32:4
表示两个比相等的式子,叫作比例。
组成比例的四个数,叫作比例的项。两端的两项
叫作比例的外项,中间的两项叫作比例的内项。
例如:
16 :2=32:4
外项
内项
16 :2=32:4 也可以写成
在比例里,两个外项与两个内项之间有什么关系呢?
分别算出两个外项和两个内项的和、差、积、商,看看有什么发现?
我发现两个外项的积等于两个内项的积。
两个外项的积等于两个内项的积。
这是不是一个规律呢?我们来验证一下!
40 :2=60:3
两外项的积:40×3=120
两内项的积:2×60=120
两外项的积:80×5=400
两内项的积:100×4=400
在比例里,两个外项的积等于两个
内项的积 ,这就是比例的基本性质。
根据比例的基本性质,可以求比例的未知项。
你能求出下面比例中的未知项吗?
像上面这样,求比例中的未知项,叫作解比例。
典题精讲
运用比例的基本性质,判断下面每组中两个比能否组成比例
3.6 : 1.8 和 0.5 : 0.25
1.4 : 2 和 5 : 10
解题思路:
根据比例的基本性质,只要计算内、外项之积是否相等就可以了。
典题精讲
3.6 : 1.8 和 0.5 : 0.25
因为 3.6×0.25=0.9 1.8×0.5=0.9
解答:
左边=右边
所以,这两个比能组成比例。
3.6:1.8=0.5:0.25
典题精讲
1.4 : 2 和 5 : 10
因为1.4×10=14 , 2×5=10。
解答:
左边≠右边
所以 这两个比不能组成比例。
易错题型
2、如果9a=8b,那么a:b= ( ) : ( )
y x
想:9和a必定是同一项,8和b也同为一项。
8 9
想:3和y必定是同一项,5和x也同为一项。
学以致用
1.下面哪组中的两个比可以组成比例?把组成的比例写出来。
② 20∶5 和 1∶4
因为:20∶5 = 4
所以: 20∶5和1∶4不能组成比例。
1∶4 = 0.25
左边 ≠ 右边
学以致用
2.填空。
①如果两个比的比值相等,那么这两个比就
( )比例。
②一个比例,等号左边的比和等号右边的比
一定是( )的。
能组成
相等
学以致用
3、指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
外项
内项
外项
内项
学以致用
0.6 ∶0.2
∶
=
3
4
1
4
3、指出下面比例的外项和内项。
外项
内项
外项
内项
∶
=
6 ∶4
1
2
1
3
学以致用
4. 在6:5=30:25这个比例中,外项是( )和( ),内项是( )和( )。根据比例的基本性质可以写成( )×( )=( )×( )。
6
25
5
30
6
25
5
30
学以致用
比例的意义
因为 14:21 =
2
3
6:9=
2
3
2
3
2
3
=
所以 这两个比能组成比例.
14:21=6:9
5.用两种方法判断14:21和6:9能否组成比例.
学以致用
比例的基本性质
因为 14×9=126 21×6=126
5.用两种方法判断14:21和6:9能否组成比例.
126 = 126
所以 这两个比能组成比例。
14:21=6:9
学以致用
6、解比例
课堂小结
这节课,我们学习了比例的意义和基本性质:两外项的积等于两内项的积。学会运用比例的基本性质去解比例,你学会了吗?
第5单元啤酒生产中的数学
1.比例的意义和基本性质
学习目标
●理解比例的意义和基本性质。掌握比例各部分的名称,能正确读写、比例。
●理解并掌握比例的基本性质,会判断两个比能否组成比例。
●通过自主学习,经历探究的过程,体验数学学习的快乐,培养学生负责、团结合作的精神。
复习导入
什么叫作比?
什么叫作比值?
两个数相除,叫作两个数的比。
比的前项除以后项的商,叫作比值。
复习导入
求下列各比的比值。
4.5:9
12:16
6:1.5
情景导入
第一天 第二天
运输次数 2 4
运输量(吨) 16 32
第一天 第二天
运输次数 2 4
运输量(吨) 16 32
你能提出什么问题?
合作探究
运输量和运输次数的比各是多少?它们有什么关系?
第一天 第二天
运输次数 2 4
运输量(吨) 16 32
第一天运输量和运输次数的比是:
16 :2
第二天运输量和运输次数的比是:
32 :4
我发现运输量和运输次的比数的比值相等。
16 :2=8
32 :4=8
两个比相等,可以写成下面的式子:
16 :2=32:4
表示两个比相等的式子,叫作比例。
组成比例的四个数,叫作比例的项。两端的两项
叫作比例的外项,中间的两项叫作比例的内项。
例如:
16 :2=32:4
外项
内项
16 :2=32:4 也可以写成
在比例里,两个外项与两个内项之间有什么关系呢?
分别算出两个外项和两个内项的和、差、积、商,看看有什么发现?
我发现两个外项的积等于两个内项的积。
两个外项的积等于两个内项的积。
这是不是一个规律呢?我们来验证一下!
40 :2=60:3
两外项的积:40×3=120
两内项的积:2×60=120
两外项的积:80×5=400
两内项的积:100×4=400
在比例里,两个外项的积等于两个
内项的积 ,这就是比例的基本性质。
根据比例的基本性质,可以求比例的未知项。
你能求出下面比例中的未知项吗?
像上面这样,求比例中的未知项,叫作解比例。
典题精讲
运用比例的基本性质,判断下面每组中两个比能否组成比例
3.6 : 1.8 和 0.5 : 0.25
1.4 : 2 和 5 : 10
解题思路:
根据比例的基本性质,只要计算内、外项之积是否相等就可以了。
典题精讲
3.6 : 1.8 和 0.5 : 0.25
因为 3.6×0.25=0.9 1.8×0.5=0.9
解答:
左边=右边
所以,这两个比能组成比例。
3.6:1.8=0.5:0.25
典题精讲
1.4 : 2 和 5 : 10
因为1.4×10=14 , 2×5=10。
解答:
左边≠右边
所以 这两个比不能组成比例。
易错题型
2、如果9a=8b,那么a:b= ( ) : ( )
y x
想:9和a必定是同一项,8和b也同为一项。
8 9
想:3和y必定是同一项,5和x也同为一项。
学以致用
1.下面哪组中的两个比可以组成比例?把组成的比例写出来。
② 20∶5 和 1∶4
因为:20∶5 = 4
所以: 20∶5和1∶4不能组成比例。
1∶4 = 0.25
左边 ≠ 右边
学以致用
2.填空。
①如果两个比的比值相等,那么这两个比就
( )比例。
②一个比例,等号左边的比和等号右边的比
一定是( )的。
能组成
相等
学以致用
3、指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
外项
内项
外项
内项
学以致用
0.6 ∶0.2
∶
=
3
4
1
4
3、指出下面比例的外项和内项。
外项
内项
外项
内项
∶
=
6 ∶4
1
2
1
3
学以致用
4. 在6:5=30:25这个比例中,外项是( )和( ),内项是( )和( )。根据比例的基本性质可以写成( )×( )=( )×( )。
6
25
5
30
6
25
5
30
学以致用
比例的意义
因为 14:21 =
2
3
6:9=
2
3
2
3
2
3
=
所以 这两个比能组成比例.
14:21=6:9
5.用两种方法判断14:21和6:9能否组成比例.
学以致用
比例的基本性质
因为 14×9=126 21×6=126
5.用两种方法判断14:21和6:9能否组成比例.
126 = 126
所以 这两个比能组成比例。
14:21=6:9
学以致用
6、解比例
课堂小结
这节课,我们学习了比例的意义和基本性质:两外项的积等于两内项的积。学会运用比例的基本性质去解比例,你学会了吗?
