第2章机械振动综合训练(Word版含答案)
文档属性
| 名称 | 第2章机械振动综合训练(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 157.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-23 09:25:51 | ||
图片预览





文档简介
第2章机械振动
一、选择题(共15题)
1.单摆是一种理想化模型。如图所示,长为l的轻绳下端拴着一个可视为质点的小球,上端固定在倾角为θ的光滑斜面上,这个装置也可以等效为“单摆”。当摆球在斜面所在的平面内做小摆角振动时,其周期为(重力加速度为g) ( )
A.T=2π B.T=2π
C.T=2π D.以上答案都不对
2.如图所示,一质点做简谐运动,O点为平衡位置,质点先后以相同的速度依次通过M、N两点,历时1 s,质点通过N点后再经过1 s又第2次通过N点,在这2 s内质点通过的总路程为12 cm。则质点的振动周期和振幅分别为 ( )
A.3 s,6 cm B.4 s,9 cm C.4 s,6 cm D.2 s,8 cm
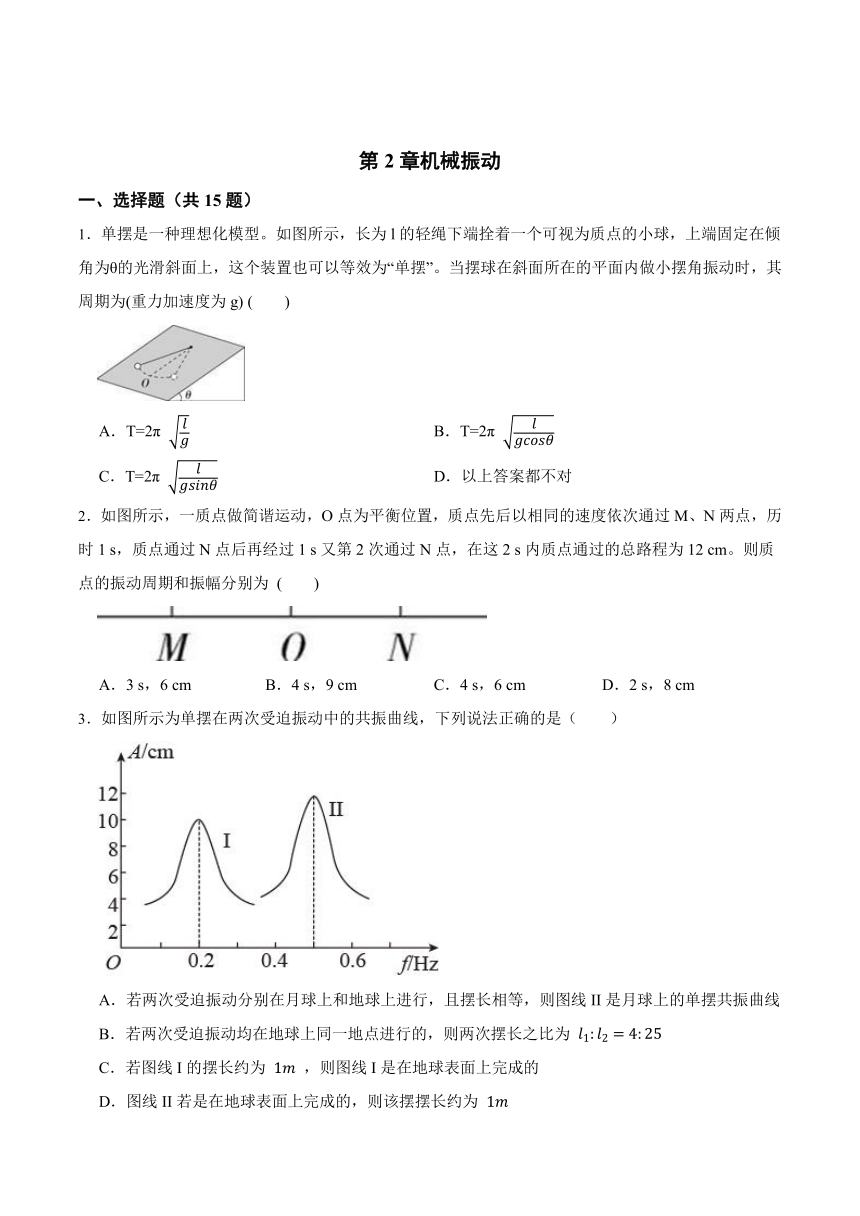
3.如图所示为单摆在两次受迫振动中的共振曲线,下列说法正确的是( )
A.若两次受迫振动分别在月球上和地球上进行,且摆长相等,则图线II是月球上的单摆共振曲线
B.若两次受迫振动均在地球上同一地点进行的,则两次摆长之比为
C.若图线I的摆长约为 ,则图线I是在地球表面上完成的
D.图线II若是在地球表面上完成的,则该摆摆长约为
4.如图所示,倾角为 的光滑绝缘斜面底端固定一劲度系数为 的绝缘轻弹簧,另一端连接一电量为 ,质量m的小球A,斜面上端固定一带电量也为 的小球B,当A静止时, 间距为d。现用一接地导线突然接触B,使B带电量瞬间减为零,已知静电力常量为 ,下列说法正确的是
A.小球A将做简谐运动,回复力满足 ,其中x为相对平衡位置的位移
B.小球A向上运动距离为 时速度达到最大
C.若满足关系式 ,A将能向上运动到与B接触
D.若保持B的带电量不变,给A一沿斜面向下初速度,A也将做简谐运动
5.如图所示,质量为m1的物体A放置在质量为m2的物体B上,B与弹簧相连,它们一起在光滑水平面上做简谐运动,振动过程中A、B之间无相对运动,设弹簧劲度系数为k,当物体离开平衡位置的位移为x时,A受到的回复力的大小等于 ( )
A.0 B.kx C. kx D. kx
6.质点做简谐运动,在其加速度减小的过程中,该质点( )
A.正向平衡位置运动,速度增大
B.正向平衡位置运动,速度减小
C.正远离平衡位置运动,速度增大
D.正远离平衡位置运动,速度减小
7.如图所示,一轻质弹簧上端固定在天花板上,下端连接一物块,物块沿竖直方向以O点为中心点,在C、D之间做周期为T的简谐运动。已知在t1时刻物块的动量为p、动能为Ek。下列说法中正确的是( )
A.如果在t2时刻物块的动量也为p,则t2-t1的最小值为T
B.如果在t2时刻物块的动能也为Ek,则t2-t1的最小值为T
C.当物块通过O点时,其加速度最小
D.当物块运动至C点时,其加速度最小
8.如图所示,弹簧振子在dc间振动,振子从a到b历时0.2s,振子经a、b两点时速度相同,若它从b再回到a的最短时间为0.4s,则该振子的振动周期为( )
A.0.6s B.0.8s C.1.0s D.1.2s
9.如图所示为波沿着一条固定的绳子向右刚好传播到B点时的波形,由图可判断出A点刚开始振动的方向是( )
A.向左 B.向右 C.向下 D.向上
10.压路机是常用的工程机械,有普通压路机(平稳行走)和振动式压路机(一边上下振动一边行走),振动式压路机的振动是由旋转的偏心轮引起的,如果一台振动式压路机的偏心轮以240r/min的转速运行。关于这台振动式压路机的振动频率以及对地面压力的最大值和等质量的普通压路机对地面压力相比,下列选项正确的是( )
A.振动频率4Hz,压力较小 B.振动频率0.25Hz,压力较小
C.振动频率4Hz,压力较大 D.振动频率0.25Hz,压力较大
11.在一单摆装置中,摆动物体是个装满水的空心小球,球的正下方有一小孔,当摆开始以小角度摆动时,让水从球中连续流出,直到流完为止,由此摆球的周期将( )
A.逐渐增大 B.逐渐减小
C.先增大后减小 D.先减小后增大
12.如图所示,两根完全相同的弹簧和一根张紧的细线将甲、乙两物块束缚在光滑水平面上,已知甲的质量是乙的质量的4倍,弹簧振子做简谐运动的周期T=2π ,式中m为振子的质量,k为弹簧的劲度系数。细线突然断开后,两物块都开始做简谐运动,在运动过程中( )
A.甲的振幅是乙的振幅的4倍
B.甲的振幅等于乙的振幅
C.甲的最大速度是乙的最大速度的
D.甲的振动周期是乙的振动周期的2倍
13.如图甲所示,弹簧振子以点 为平衡位置,在A、 两点之间做简谐运动,取向右为正方向,振子的位移 随时间 的变化如图乙所示。下列说法正确的是( )
A. 时,振子的速度方向向左
B. 时,振子在 点右侧 处
C. 到 的时间内,振子的速度逐渐增大
D. 到 的时间内,振子的加速度逐渐增大
14.下列说法正确的是( )
A.军队士兵过桥时使用便步,是为了防止桥发生共振现象
B.同一单摆,在月球表面简谐振动的周期等于在地面表面简谐振动的周期
C.一弹簧振子的位移y随时间t变化的关系式为y=0.1sin2.5πt(单位都是国际单位制),在t=0.2s时,振子的运动速度为零
D.做简谐振动的物体,经过同一位置时,速度可能不同
15.如图所示单摆在竖直平面内的A、C之间做简谐运动,O点为单摆的固定悬点,B点为运动中的最低位置,则下列说法正确的是( )
A.摆球在A点和C点处,速度为零,故细线拉力为零,但回复力不为零
B.摆球由A点向B点摆动过程中,细线拉力增大,但回复力减小
C.摆球在B点处,重力势能最小,合力为零
D.摆球在B点处,动能最大,细线拉力也最大
二、填空题
16.图中的双线摆,绳的质量可以不计,当摆球垂直线面做简谐运动时,其周期为 s.
17.一弹簧振子的位移y随时间t变化的关系式为 ,位移y的单位为m,时间t的单位为s。在 时,振子的运动速度为 ,该振子在固有频率为 的周期性驱动力的作用下做受迫振动时振幅最大,则 为 。
18.一单摆的摆长为L,将摆球向左拉至水平标志线上(图中虚线)。由静止释放摆球,当摆球运动至最低点时,摆线碰到障碍物P,摆球继续摆动。用频闪相机长时间拍摄,得到图示照片,则摆线的悬点O与障碍物P在竖直方向之间的距离为 。不计空气阻力,摆线向右碰到障碍物的瞬间,摆球的角速度突然增大,其原因是: 。
19.如图,一弹簧振子沿x轴做简谐运动,振子零时刻向右经过A点, 后第一次到达B点,已知振子经过A、B两点时的速度大小相等, 内经过的路程为0.4m。该弹簧振子的周期为 s,振幅为 m。
三、综合题
20.一个小球和轻质弹簧组成的系统按 的规律振动。
(1)求该振动的周期、频率、振幅和初相;
(2)另一简谐运动的表达式为 ,求它们的相位差。
21.有一个摆长为L的单摆,它的摆球质量为m,从与竖直方向成θ的位置无初速开始运动,重力加速度为g,以平衡位置为参考平面,求:
(1)单摆的总机械能;
(2)在偏角很小的情况下,从开始运动到摆球第一次经过最低位置需要的时间。
22.如图所示,弹簧振子在光滑水平面上以振幅A做简谐运动,质量为M的滑块上面放一个质量为m的砝码,砝码随滑块一起做简谐运动,已知弹簧的劲度系数为k,试求:
(1)使砝码随滑块一起振动的回复力是什么力 它跟位移成正比的比例常数k'等于多少
(2)当滑块运动到振幅一半位置时,砝码所受回复力有多大 方向如何
(3)当砝码与滑块的动摩擦因数为 时,要使砝码与滑块不发生相对滑动的最大振幅为多大
23.减振器,英文shockabsorber,是为加速车架与车身振动的衰减,以改善汽车的行驶舒适性的汽配原件,在大多数汽车的悬架系统内部都装有减震器。汽车的重力一般支撑在固定于轴承上的若干弹簧上,弹簧套在减震器上,两者同时起到改善作用。为了研究方便,我们把两者简化成一个等效劲度系数为 的“弹簧”。汽车开始运动时,在振幅较小的情况下,其上下自由振动的频率满足 ( 为弹簧的压缩长度),若人体可以看成一个弹性体,其固有频率约为2Hz,已知汽车的质量为600kg,每个人的质量为70kg。求:
(1)汽车的振动频率与人体固有频率相等时l的大小;
(2)这辆车乘坐几个人时,人感觉到最难受。
答案部分
1.C
【解答】由题意可知,该“单摆”的“等效重力加速度”为g'=g sin θ,由单摆的周期公式可知该等效“单摆”的周期T=2π .
故答案为:C。
2.C
【解答】做简谐运动的质点,先后以相同的速度通过M、N两点,可判定M、N两点关于平衡位置O对称,所以质点由M到O所用的时间与由O到N所用的时间相等,则质点由平衡位置O到N点所用的时间t1=0.5 s;因通过N点后再经过t=1 s质点以方向相反、大小相等的速度再次通过N点,则知质点从N点到最大位移处所用的时间t2=0.5 s,因此,质点振动的周期是T=4×(t1+t2)=4 s。题中2 s内质点通过的总路程为振幅的2倍,所以振幅A= cm=6 cm。
故答案为:C。
3.D
【解答】A.若两次受迫振动分别在月球上和地球上进行,因为图线Ⅰ单摆的固有频率较小,则固有周期较大,根据
可知,周期大的重力加速度小,则图线Ⅰ是月球上单摆的共振曲线。A不符合题意;
B.若两次受迫振动均在地球上同一地点进行的,则重力加速度相等,因为固有频率比为2:5,则固有周期比为5:2,根据
知摆长比为25:4,B不符合题意;
CD.图线Ⅱ若是在地球表面上完成的,则固有频率为0.5Hz,则
解得L=1m
C不符合题意,D符合题意;
故答案为:D。
4.C
【解答】A.在平衡位置时,弹簧压缩量为x1,则有 k1x1=mgsinθ
某时刻,距离平衡位置x处,回复力F回=-k1(x+x1)+mgsinθ=-k1x
式中k1为弹簧的劲度系数,A不符合题意;
B.初始时刻弹簧的压缩量为x2,根据平衡条件
当小球的速度最大时满足k1x1=mgsinθ
因此小球向上移动的距离为
故 B不符合题意;
C.若使得A与B接触需满足
即
C符合题意;
D.若保持B的带电量不变,平衡位置应在x2,设某时刻,距离平衡位置为x,此时回复力
不满足简谐振动条件,因此不是简谐振动,D不符合题意。
故答案为:C。
5.C
【解答】物体A和B整体做简谐运动,当它们离开平衡位置的位移为x时,回复力的大小即弹簧弹力大小为kx,以整体为研究对象,有kx=(m1+m2)a,则整体的加速度a= ;以物体A为研究对象,使其产生加速度的力为物体B对它的静摩擦力Ff,由牛顿第二定律得Ff=m1a= kx,A、B、D不符合题意,C符合题意。
故答案为:C。
6.A
【解答】质点加速度减小,则回复力减小,根据回复力位移关系可知,位移减小,故正向平衡位置运动,速度增大,A符合题意BCD不符合题意。
故答案为:A。
7.C
【解答】物块做简谐运动,物块同向经过关于平衡位置对称的两点时动量相等,所以如果在t2时刻物块的动量也为p,t2﹣t1的最小值小于等于 .A不符合题意;物块经过同一位置或关于平衡位置对称的位置时动能相等,如果在t2时刻物块的动能也为Ek,则t2﹣t1的最小值可以小于T,B不符合题意;图中O点是平衡位置,根据 知,物块经过O点时位移最小,则其加速度最小,C符合题意;物块运动至C点时,位移最大,其加速度最大,D不符合题意。
故答案为:C
8.B
【解答】由于振子在a、b两点的速度相同,则a、b两点关于O点是对称的,所以O到b点的时间为0.1s,而从b再回到a的最短时间为0.4s,则从b再回到b的最短时间为0.2s,所以从b到最大位移处的最短时间为0.1s,因此振子的振动周期为 T=0.8s,
故答案为:B.
9.D
【解答】绳子上向右传播的横波,质点的振动方向与传播方向垂直,不可能沿水平方向.A、B均错误.图示时刻B振动方向向上,则A点刚开始的振动方向向上.C不符合题意,D符合题意.
故答案为:D
10.C
【解答】由题意可知,振动式压路机的偏心轮转动频率为
故振动频率为4Hz,对偏心轮边缘的一点,转到最低点时满足
可得
故对应的压力较大,C符合题意。
故答案为:C。
11.C
【解答】单摆小角度摆动,做简谐运动的周期为 ,式中L为摆长,其值为悬点到摆动物体重心之间的距离,当小球装满水时,重心在球心,水流完后,重心也在球心,但水刚流出过程中重心要降低,因此,在水的整个流出过程中,重心位置先下降后上升,即摆长Ll先增大后减小,所以摆动周期将先增大后减小。ABD不符合题意,C符合题意。
故答案为:C。
12.B,C,D
【解答】AB.线断开前,两根弹簧伸长的长度相同,离开平衡位置的最大距离相同,即两物块的振幅一定相同,A不符合题意,B符合题意;
C.线断开的瞬间,两根弹簧的弹性势能相同,到达平衡位置时,甲、乙的动能最大且相同,由于甲的质量大于乙的质量,由 可知,甲的最大速度一定是乙的最大速度的 ,C符合题意;
D.根据 可知,甲的振动周期是乙的振动周期的2倍,D符合题意。
故答案为:BCD。
13.A,C,D
【解答】A.由图可知, 时,振子在平衡位置向负方向运动,所以速度方向向左,A符合题意;
B. 时,振子远离平衡位置运动,速度逐渐减小,应在O点右侧大于6cm处,B不符合题意;
C. 到 的时间内,振子向平衡位置运动,速度逐渐增大,C符合题意;
D. 到 的时间内,振子远离平衡位置运动,加速度逐渐增大,D符合题意。
故答案为:ACD。
14.A,C,D
【解答】A.如果军队过桥使用齐步,频率相同,如果与桥的固有频率相同,发生共振,引发事故,所以军队士兵过桥时使用便步,A符合题意
B.根据单摆振动周期方程: ,因为重力加速度不一样,周期不一样,B不符合题意
C.当t=0.2s时,y=0.1m,振子处于最大位移处,速度为零,C符合题意
D.做简谐振动的物体,经过同一位置时,速度可能不同,如从平衡位置到最大位移处,和从最大位移处到平衡位置过程中通过同一位置,速度大小相等,方向相反,D符合题意
故答案为:ACD
15.B,D
【解答】假设摆动过程中,细线与竖直方向夹角为 ,重力沿细线方向分力为 ,垂直于细线方向分力为 。
A.摆球在A点和C点处,速度为零,沿细线方向的合力为零,有
即细线的拉力与重力沿细线方向分力等大,不为零,回复力与重力沿切向方向的分力等大,也不为零。A不符合题意;
B.摆球由A点向B点摆动过程中,速度变大,根据
可得细线拉力增大,回复力减小。B符合题意;
CD.摆球从最高点摆到B点过程中,重力做正功,其重力势能一直在减小,动能一直在增加,所以摆球在B点处,重力势能最小,动能最大。在B点处对摆球受力分析,可得
可知,此时细线拉力最大,合力不为零。C不符合题意;D符合题意。
故答案为:BD。
16.
【解答】如图所示,等效摆长为Lsinα,由于小球做简谐运动,由单摆的振动周期为:
17.0;1.25
【解答】由弹簧振子的振动方程可知,该振子的周期为
当
时,振子从平衡位置开始,振动了四分之一周期,即此时振子在最大位移处,所以振子的运动速度为0;
振子的固有频率为
18.;水平方向没有力的作用,线速度大小不变,但半径减小,故角速度突然增大
【解答】 设频闪相机闪光周期为 T,则由图可知,单摆在左半部分摆动时
在右半部分摆动时
根据单摆周期公式
解得
摆线向右碰到障碍物的瞬间,摆球水平方向没有力的作用,线速度大小不变,但半径减小,故角速度突然增大。
19.4;0.2
【解答】根据简谐运动对称性可知,振子零时刻向右经过A点, 后第一次到达B点,已知振子经过A、B两点时的速度大小相等,则A、B两点关于平衡位置对称,而振动经过了半个周期的运动,则周期为
从A到B经过了半个周期的振动,路程为 ,而一个完整的周期路程为0.8m,为4个振幅的路程,有
解得振幅为
20.(1)已知 ,由
得
所以频率为
由 可看出,振幅为
初相位为
(2)由
得
21.(1)解: 以平衡位置所在的水平面为参考平面,初位置的动能EK=0,重力势能EP=mgL(1-cosθ).所以E=EK+EP=mgL(1-cosθ).故单摆的总机械能为mgL(1-cosθ).
(2)解: 单摆完成一次全振动的时间T=2π ;则 .故从开始运动到摆球第一次经过最低位置需要的时间为 .
22.(1)解:使砝码随着滑块一起振动,砝码所受静摩擦力是产生砝码与滑块一起变加速运动的加速度.故M对m的静摩擦力是回复力.
其大小由牛顿第二定律有:f=ma
整体法求共同加速度a,则有
它跟位移成正比的比例常数
(2)解:当滑块运动到振动幅的一半位置时 ,回复力:
方向指向平衡位置
(3)解:从f=k′x,可以看出,当x增大时,f也增大,当f=fmax=μN时,有最大振动幅,
因此fm=mam=μmg=
k′AM
要使砝码与滑块不发生相对滑动的最大振幅
23.(1)解:当汽车的频率等于人的固有频率时
解得
(2)解:设乘车人数为n个时,人感觉到最难受,则
联立以上两式解得
一、选择题(共15题)
1.单摆是一种理想化模型。如图所示,长为l的轻绳下端拴着一个可视为质点的小球,上端固定在倾角为θ的光滑斜面上,这个装置也可以等效为“单摆”。当摆球在斜面所在的平面内做小摆角振动时,其周期为(重力加速度为g) ( )
A.T=2π B.T=2π
C.T=2π D.以上答案都不对
2.如图所示,一质点做简谐运动,O点为平衡位置,质点先后以相同的速度依次通过M、N两点,历时1 s,质点通过N点后再经过1 s又第2次通过N点,在这2 s内质点通过的总路程为12 cm。则质点的振动周期和振幅分别为 ( )
A.3 s,6 cm B.4 s,9 cm C.4 s,6 cm D.2 s,8 cm
3.如图所示为单摆在两次受迫振动中的共振曲线,下列说法正确的是( )
A.若两次受迫振动分别在月球上和地球上进行,且摆长相等,则图线II是月球上的单摆共振曲线
B.若两次受迫振动均在地球上同一地点进行的,则两次摆长之比为
C.若图线I的摆长约为 ,则图线I是在地球表面上完成的
D.图线II若是在地球表面上完成的,则该摆摆长约为
4.如图所示,倾角为 的光滑绝缘斜面底端固定一劲度系数为 的绝缘轻弹簧,另一端连接一电量为 ,质量m的小球A,斜面上端固定一带电量也为 的小球B,当A静止时, 间距为d。现用一接地导线突然接触B,使B带电量瞬间减为零,已知静电力常量为 ,下列说法正确的是
A.小球A将做简谐运动,回复力满足 ,其中x为相对平衡位置的位移
B.小球A向上运动距离为 时速度达到最大
C.若满足关系式 ,A将能向上运动到与B接触
D.若保持B的带电量不变,给A一沿斜面向下初速度,A也将做简谐运动
5.如图所示,质量为m1的物体A放置在质量为m2的物体B上,B与弹簧相连,它们一起在光滑水平面上做简谐运动,振动过程中A、B之间无相对运动,设弹簧劲度系数为k,当物体离开平衡位置的位移为x时,A受到的回复力的大小等于 ( )
A.0 B.kx C. kx D. kx
6.质点做简谐运动,在其加速度减小的过程中,该质点( )
A.正向平衡位置运动,速度增大
B.正向平衡位置运动,速度减小
C.正远离平衡位置运动,速度增大
D.正远离平衡位置运动,速度减小
7.如图所示,一轻质弹簧上端固定在天花板上,下端连接一物块,物块沿竖直方向以O点为中心点,在C、D之间做周期为T的简谐运动。已知在t1时刻物块的动量为p、动能为Ek。下列说法中正确的是( )
A.如果在t2时刻物块的动量也为p,则t2-t1的最小值为T
B.如果在t2时刻物块的动能也为Ek,则t2-t1的最小值为T
C.当物块通过O点时,其加速度最小
D.当物块运动至C点时,其加速度最小
8.如图所示,弹簧振子在dc间振动,振子从a到b历时0.2s,振子经a、b两点时速度相同,若它从b再回到a的最短时间为0.4s,则该振子的振动周期为( )
A.0.6s B.0.8s C.1.0s D.1.2s
9.如图所示为波沿着一条固定的绳子向右刚好传播到B点时的波形,由图可判断出A点刚开始振动的方向是( )
A.向左 B.向右 C.向下 D.向上
10.压路机是常用的工程机械,有普通压路机(平稳行走)和振动式压路机(一边上下振动一边行走),振动式压路机的振动是由旋转的偏心轮引起的,如果一台振动式压路机的偏心轮以240r/min的转速运行。关于这台振动式压路机的振动频率以及对地面压力的最大值和等质量的普通压路机对地面压力相比,下列选项正确的是( )
A.振动频率4Hz,压力较小 B.振动频率0.25Hz,压力较小
C.振动频率4Hz,压力较大 D.振动频率0.25Hz,压力较大
11.在一单摆装置中,摆动物体是个装满水的空心小球,球的正下方有一小孔,当摆开始以小角度摆动时,让水从球中连续流出,直到流完为止,由此摆球的周期将( )
A.逐渐增大 B.逐渐减小
C.先增大后减小 D.先减小后增大
12.如图所示,两根完全相同的弹簧和一根张紧的细线将甲、乙两物块束缚在光滑水平面上,已知甲的质量是乙的质量的4倍,弹簧振子做简谐运动的周期T=2π ,式中m为振子的质量,k为弹簧的劲度系数。细线突然断开后,两物块都开始做简谐运动,在运动过程中( )
A.甲的振幅是乙的振幅的4倍
B.甲的振幅等于乙的振幅
C.甲的最大速度是乙的最大速度的
D.甲的振动周期是乙的振动周期的2倍
13.如图甲所示,弹簧振子以点 为平衡位置,在A、 两点之间做简谐运动,取向右为正方向,振子的位移 随时间 的变化如图乙所示。下列说法正确的是( )
A. 时,振子的速度方向向左
B. 时,振子在 点右侧 处
C. 到 的时间内,振子的速度逐渐增大
D. 到 的时间内,振子的加速度逐渐增大
14.下列说法正确的是( )
A.军队士兵过桥时使用便步,是为了防止桥发生共振现象
B.同一单摆,在月球表面简谐振动的周期等于在地面表面简谐振动的周期
C.一弹簧振子的位移y随时间t变化的关系式为y=0.1sin2.5πt(单位都是国际单位制),在t=0.2s时,振子的运动速度为零
D.做简谐振动的物体,经过同一位置时,速度可能不同
15.如图所示单摆在竖直平面内的A、C之间做简谐运动,O点为单摆的固定悬点,B点为运动中的最低位置,则下列说法正确的是( )
A.摆球在A点和C点处,速度为零,故细线拉力为零,但回复力不为零
B.摆球由A点向B点摆动过程中,细线拉力增大,但回复力减小
C.摆球在B点处,重力势能最小,合力为零
D.摆球在B点处,动能最大,细线拉力也最大
二、填空题
16.图中的双线摆,绳的质量可以不计,当摆球垂直线面做简谐运动时,其周期为 s.
17.一弹簧振子的位移y随时间t变化的关系式为 ,位移y的单位为m,时间t的单位为s。在 时,振子的运动速度为 ,该振子在固有频率为 的周期性驱动力的作用下做受迫振动时振幅最大,则 为 。
18.一单摆的摆长为L,将摆球向左拉至水平标志线上(图中虚线)。由静止释放摆球,当摆球运动至最低点时,摆线碰到障碍物P,摆球继续摆动。用频闪相机长时间拍摄,得到图示照片,则摆线的悬点O与障碍物P在竖直方向之间的距离为 。不计空气阻力,摆线向右碰到障碍物的瞬间,摆球的角速度突然增大,其原因是: 。
19.如图,一弹簧振子沿x轴做简谐运动,振子零时刻向右经过A点, 后第一次到达B点,已知振子经过A、B两点时的速度大小相等, 内经过的路程为0.4m。该弹簧振子的周期为 s,振幅为 m。
三、综合题
20.一个小球和轻质弹簧组成的系统按 的规律振动。
(1)求该振动的周期、频率、振幅和初相;
(2)另一简谐运动的表达式为 ,求它们的相位差。
21.有一个摆长为L的单摆,它的摆球质量为m,从与竖直方向成θ的位置无初速开始运动,重力加速度为g,以平衡位置为参考平面,求:
(1)单摆的总机械能;
(2)在偏角很小的情况下,从开始运动到摆球第一次经过最低位置需要的时间。
22.如图所示,弹簧振子在光滑水平面上以振幅A做简谐运动,质量为M的滑块上面放一个质量为m的砝码,砝码随滑块一起做简谐运动,已知弹簧的劲度系数为k,试求:
(1)使砝码随滑块一起振动的回复力是什么力 它跟位移成正比的比例常数k'等于多少
(2)当滑块运动到振幅一半位置时,砝码所受回复力有多大 方向如何
(3)当砝码与滑块的动摩擦因数为 时,要使砝码与滑块不发生相对滑动的最大振幅为多大
23.减振器,英文shockabsorber,是为加速车架与车身振动的衰减,以改善汽车的行驶舒适性的汽配原件,在大多数汽车的悬架系统内部都装有减震器。汽车的重力一般支撑在固定于轴承上的若干弹簧上,弹簧套在减震器上,两者同时起到改善作用。为了研究方便,我们把两者简化成一个等效劲度系数为 的“弹簧”。汽车开始运动时,在振幅较小的情况下,其上下自由振动的频率满足 ( 为弹簧的压缩长度),若人体可以看成一个弹性体,其固有频率约为2Hz,已知汽车的质量为600kg,每个人的质量为70kg。求:
(1)汽车的振动频率与人体固有频率相等时l的大小;
(2)这辆车乘坐几个人时,人感觉到最难受。
答案部分
1.C
【解答】由题意可知,该“单摆”的“等效重力加速度”为g'=g sin θ,由单摆的周期公式可知该等效“单摆”的周期T=2π .
故答案为:C。
2.C
【解答】做简谐运动的质点,先后以相同的速度通过M、N两点,可判定M、N两点关于平衡位置O对称,所以质点由M到O所用的时间与由O到N所用的时间相等,则质点由平衡位置O到N点所用的时间t1=0.5 s;因通过N点后再经过t=1 s质点以方向相反、大小相等的速度再次通过N点,则知质点从N点到最大位移处所用的时间t2=0.5 s,因此,质点振动的周期是T=4×(t1+t2)=4 s。题中2 s内质点通过的总路程为振幅的2倍,所以振幅A= cm=6 cm。
故答案为:C。
3.D
【解答】A.若两次受迫振动分别在月球上和地球上进行,因为图线Ⅰ单摆的固有频率较小,则固有周期较大,根据
可知,周期大的重力加速度小,则图线Ⅰ是月球上单摆的共振曲线。A不符合题意;
B.若两次受迫振动均在地球上同一地点进行的,则重力加速度相等,因为固有频率比为2:5,则固有周期比为5:2,根据
知摆长比为25:4,B不符合题意;
CD.图线Ⅱ若是在地球表面上完成的,则固有频率为0.5Hz,则
解得L=1m
C不符合题意,D符合题意;
故答案为:D。
4.C
【解答】A.在平衡位置时,弹簧压缩量为x1,则有 k1x1=mgsinθ
某时刻,距离平衡位置x处,回复力F回=-k1(x+x1)+mgsinθ=-k1x
式中k1为弹簧的劲度系数,A不符合题意;
B.初始时刻弹簧的压缩量为x2,根据平衡条件
当小球的速度最大时满足k1x1=mgsinθ
因此小球向上移动的距离为
故 B不符合题意;
C.若使得A与B接触需满足
即
C符合题意;
D.若保持B的带电量不变,平衡位置应在x2,设某时刻,距离平衡位置为x,此时回复力
不满足简谐振动条件,因此不是简谐振动,D不符合题意。
故答案为:C。
5.C
【解答】物体A和B整体做简谐运动,当它们离开平衡位置的位移为x时,回复力的大小即弹簧弹力大小为kx,以整体为研究对象,有kx=(m1+m2)a,则整体的加速度a= ;以物体A为研究对象,使其产生加速度的力为物体B对它的静摩擦力Ff,由牛顿第二定律得Ff=m1a= kx,A、B、D不符合题意,C符合题意。
故答案为:C。
6.A
【解答】质点加速度减小,则回复力减小,根据回复力位移关系可知,位移减小,故正向平衡位置运动,速度增大,A符合题意BCD不符合题意。
故答案为:A。
7.C
【解答】物块做简谐运动,物块同向经过关于平衡位置对称的两点时动量相等,所以如果在t2时刻物块的动量也为p,t2﹣t1的最小值小于等于 .A不符合题意;物块经过同一位置或关于平衡位置对称的位置时动能相等,如果在t2时刻物块的动能也为Ek,则t2﹣t1的最小值可以小于T,B不符合题意;图中O点是平衡位置,根据 知,物块经过O点时位移最小,则其加速度最小,C符合题意;物块运动至C点时,位移最大,其加速度最大,D不符合题意。
故答案为:C
8.B
【解答】由于振子在a、b两点的速度相同,则a、b两点关于O点是对称的,所以O到b点的时间为0.1s,而从b再回到a的最短时间为0.4s,则从b再回到b的最短时间为0.2s,所以从b到最大位移处的最短时间为0.1s,因此振子的振动周期为 T=0.8s,
故答案为:B.
9.D
【解答】绳子上向右传播的横波,质点的振动方向与传播方向垂直,不可能沿水平方向.A、B均错误.图示时刻B振动方向向上,则A点刚开始的振动方向向上.C不符合题意,D符合题意.
故答案为:D
10.C
【解答】由题意可知,振动式压路机的偏心轮转动频率为
故振动频率为4Hz,对偏心轮边缘的一点,转到最低点时满足
可得
故对应的压力较大,C符合题意。
故答案为:C。
11.C
【解答】单摆小角度摆动,做简谐运动的周期为 ,式中L为摆长,其值为悬点到摆动物体重心之间的距离,当小球装满水时,重心在球心,水流完后,重心也在球心,但水刚流出过程中重心要降低,因此,在水的整个流出过程中,重心位置先下降后上升,即摆长Ll先增大后减小,所以摆动周期将先增大后减小。ABD不符合题意,C符合题意。
故答案为:C。
12.B,C,D
【解答】AB.线断开前,两根弹簧伸长的长度相同,离开平衡位置的最大距离相同,即两物块的振幅一定相同,A不符合题意,B符合题意;
C.线断开的瞬间,两根弹簧的弹性势能相同,到达平衡位置时,甲、乙的动能最大且相同,由于甲的质量大于乙的质量,由 可知,甲的最大速度一定是乙的最大速度的 ,C符合题意;
D.根据 可知,甲的振动周期是乙的振动周期的2倍,D符合题意。
故答案为:BCD。
13.A,C,D
【解答】A.由图可知, 时,振子在平衡位置向负方向运动,所以速度方向向左,A符合题意;
B. 时,振子远离平衡位置运动,速度逐渐减小,应在O点右侧大于6cm处,B不符合题意;
C. 到 的时间内,振子向平衡位置运动,速度逐渐增大,C符合题意;
D. 到 的时间内,振子远离平衡位置运动,加速度逐渐增大,D符合题意。
故答案为:ACD。
14.A,C,D
【解答】A.如果军队过桥使用齐步,频率相同,如果与桥的固有频率相同,发生共振,引发事故,所以军队士兵过桥时使用便步,A符合题意
B.根据单摆振动周期方程: ,因为重力加速度不一样,周期不一样,B不符合题意
C.当t=0.2s时,y=0.1m,振子处于最大位移处,速度为零,C符合题意
D.做简谐振动的物体,经过同一位置时,速度可能不同,如从平衡位置到最大位移处,和从最大位移处到平衡位置过程中通过同一位置,速度大小相等,方向相反,D符合题意
故答案为:ACD
15.B,D
【解答】假设摆动过程中,细线与竖直方向夹角为 ,重力沿细线方向分力为 ,垂直于细线方向分力为 。
A.摆球在A点和C点处,速度为零,沿细线方向的合力为零,有
即细线的拉力与重力沿细线方向分力等大,不为零,回复力与重力沿切向方向的分力等大,也不为零。A不符合题意;
B.摆球由A点向B点摆动过程中,速度变大,根据
可得细线拉力增大,回复力减小。B符合题意;
CD.摆球从最高点摆到B点过程中,重力做正功,其重力势能一直在减小,动能一直在增加,所以摆球在B点处,重力势能最小,动能最大。在B点处对摆球受力分析,可得
可知,此时细线拉力最大,合力不为零。C不符合题意;D符合题意。
故答案为:BD。
16.
【解答】如图所示,等效摆长为Lsinα,由于小球做简谐运动,由单摆的振动周期为:
17.0;1.25
【解答】由弹簧振子的振动方程可知,该振子的周期为
当
时,振子从平衡位置开始,振动了四分之一周期,即此时振子在最大位移处,所以振子的运动速度为0;
振子的固有频率为
18.;水平方向没有力的作用,线速度大小不变,但半径减小,故角速度突然增大
【解答】 设频闪相机闪光周期为 T,则由图可知,单摆在左半部分摆动时
在右半部分摆动时
根据单摆周期公式
解得
摆线向右碰到障碍物的瞬间,摆球水平方向没有力的作用,线速度大小不变,但半径减小,故角速度突然增大。
19.4;0.2
【解答】根据简谐运动对称性可知,振子零时刻向右经过A点, 后第一次到达B点,已知振子经过A、B两点时的速度大小相等,则A、B两点关于平衡位置对称,而振动经过了半个周期的运动,则周期为
从A到B经过了半个周期的振动,路程为 ,而一个完整的周期路程为0.8m,为4个振幅的路程,有
解得振幅为
20.(1)已知 ,由
得
所以频率为
由 可看出,振幅为
初相位为
(2)由
得
21.(1)解: 以平衡位置所在的水平面为参考平面,初位置的动能EK=0,重力势能EP=mgL(1-cosθ).所以E=EK+EP=mgL(1-cosθ).故单摆的总机械能为mgL(1-cosθ).
(2)解: 单摆完成一次全振动的时间T=2π ;则 .故从开始运动到摆球第一次经过最低位置需要的时间为 .
22.(1)解:使砝码随着滑块一起振动,砝码所受静摩擦力是产生砝码与滑块一起变加速运动的加速度.故M对m的静摩擦力是回复力.
其大小由牛顿第二定律有:f=ma
整体法求共同加速度a,则有
它跟位移成正比的比例常数
(2)解:当滑块运动到振动幅的一半位置时 ,回复力:
方向指向平衡位置
(3)解:从f=k′x,可以看出,当x增大时,f也增大,当f=fmax=μN时,有最大振动幅,
因此fm=mam=μmg=
k′AM
要使砝码与滑块不发生相对滑动的最大振幅
23.(1)解:当汽车的频率等于人的固有频率时
解得
(2)解:设乘车人数为n个时,人感觉到最难受,则
联立以上两式解得
同课章节目录
- 第1章 碰撞与动量守恒
- 1.1 动量变化与冲量的关系
- 1.2 动量守恒定律
- 1.3 动量守恒定律的案例分析
- 1.4 美妙的守恒定律
- 第2章 机械振动
- 2.1 简谐运动
- 2.2 物体做简谐运动的原因
- 2.3 摆钟的物理原理
- 2.4 单摆振动的周期
- 2.5 受迫振动与共振
- 第3章 机械波
- 3.1 机械波的产生
- 3.2 机械波的描述
- 3.3 机械波案例分析
- 3.4 惠更斯原理 波的反射与折射
- 3.5 波的干涉与衍射
- 3.6 多普勒效应
- 第4章 光及其应用
- 4.1 光的折射
- 4.2 全反射与光导纤维
- 4.3 光的干涉
- 4.4 用双缝干涉仪测量光的波长
- 4.5 光的衍射
- 4.6 光的偏振与立体电影
- 4.7 激光
