1.4美妙的守恒定律综合训练(Word版含答案)
文档属性
| 名称 | 1.4美妙的守恒定律综合训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 619.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-23 09:41:40 | ||
图片预览



文档简介
1.4美妙的守恒定律
一、选择题(共15题)
1.甲乙两球在水平光滑轨道上向同一方向运动,已知它们的动量分别是p1= 5kgm/s,p2=7kgm/s,甲从后面追上乙并且发生碰撞,碰后乙球的动量变为 10kgm/s.则二球质量m1和m2间的关系可以是下面的哪几种( )
A.m2=m1 B.m2=6m1 C.m2=2m1 D.m2=3m1
2.一个质量为m的小球A在光滑的水平面上以3m/s速度向右运动,与一个质量为2m的静止的小球B发生正碰,假设碰撞过程中没有机械能损失,则碰后( )
A.A球、B球都向右运动,速度都是1m/s
B.A球向左运动,速度为1m/s;B球向右运动,速度为2m/s
C.A球向左运动,速度为5m/s;B球向右运动,速度为1m/s
D.A球向右运动,速度为0.5m/s;B球向右运动,速度为1.25m/s
3.在光滑水平轨道上有两个小球A和B(均可看做质点),质量分别为2m和3m当两球间的距离大于L时,两球之间无相互作用;当两球间的距离等于或小于L时,两球间存在大小为F的恒定斥力,设A球从距离B球足够远处以某一初速度沿两球连线向原来静止的B球运动,如图所示,结果两球恰好接触,则该初速度大小为( )
A. B. C. D.
4.如图所示,足够长的两根光滑细杆水平平行放置(处在竖直面内),质量相等的两个小球A、B分别套在两杆上,开始时AB位置连线与杆垂直,A和B连接着一轻质弹簧,此时弹簧恰好为原长(弹簧永远在弹性限度内),现给B球一个初速度v0向右运动,则关于两小球的运动情况,下列说法正确的是( )
A.第一次两球相距最远时,B球的速度为0 B.第一次两球相距最远时,B球的速度为
C.从B球开始运动后,B球的速度不可能为零 D.第一次两球相距最远时,弹性势能最大,系统动能为0
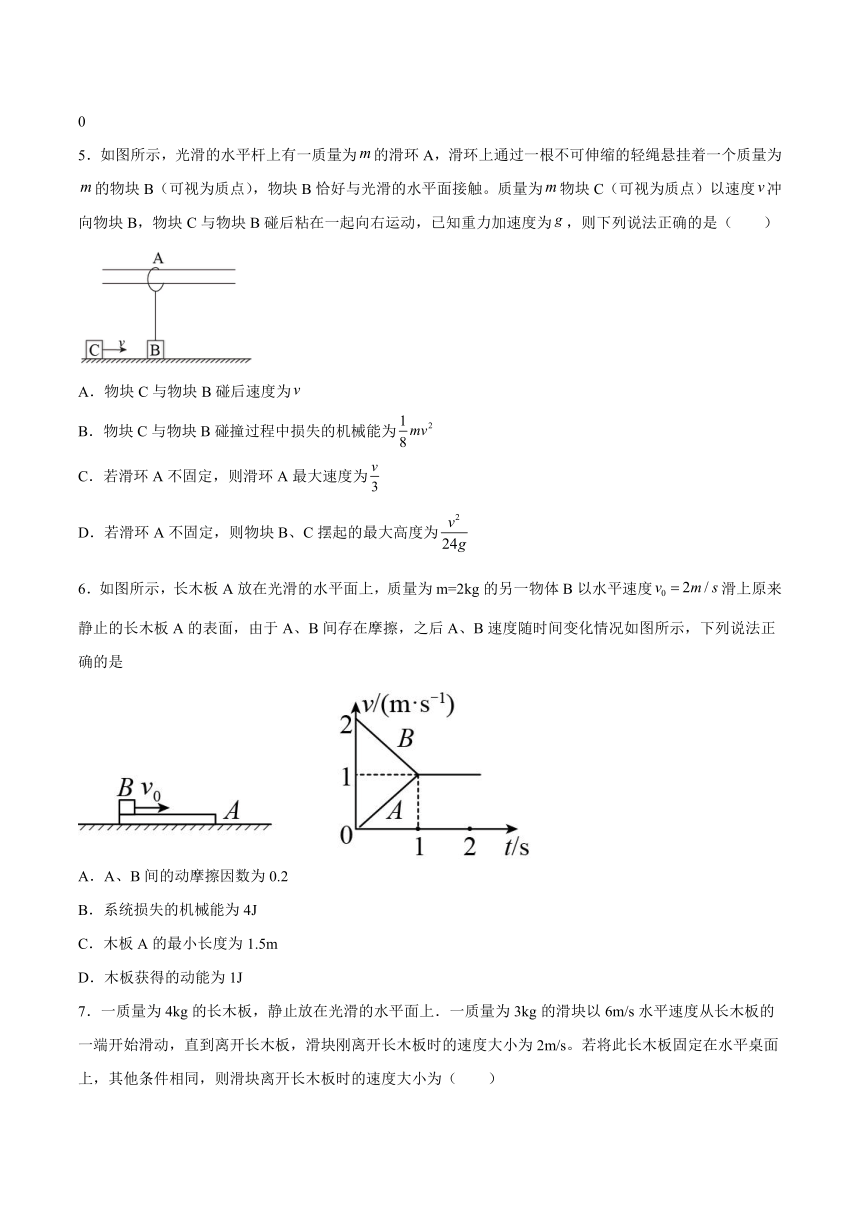
5.如图所示,光滑的水平杆上有一质量为的滑环A,滑环上通过一根不可伸缩的轻绳悬挂着一个质量为的物块B(可视为质点),物块B恰好与光滑的水平面接触。质量为物块C(可视为质点)以速度冲向物块B,物块C与物块B碰后粘在一起向右运动,已知重力加速度为,则下列说法正确的是( )
A.物块C与物块B碰后速度为
B.物块C与物块B碰撞过程中损失的机械能为
C.若滑环A不固定,则滑环A最大速度为
D.若滑环A不固定,则物块B、C摆起的最大高度为
6.如图所示,长木板A放在光滑的水平面上,质量为m=2kg的另一物体B以水平速度滑上原来静止的长木板A的表面,由于A、B间存在摩擦,之后A、B速度随时间变化情况如图所示,下列说法正确的是
A.A、B间的动摩擦因数为0.2
B.系统损失的机械能为4J
C.木板A的最小长度为1.5m
D.木板获得的动能为1J
7.一质量为4kg的长木板,静止放在光滑的水平面上.一质量为3kg的滑块以6m/s水平速度从长木板的一端开始滑动,直到离开长木板,滑块刚离开长木板时的速度大小为2m/s。若将此长木板固定在水平桌面上,其他条件相同,则滑块离开长木板时的速度大小为( )
A.2m/s B.3m/s C.4m/s D.5m/s
8.如图,质量为M的小车静止在光滑的水平面上,小车AB段是半径为R的四分之一光滑圆弧轨道,BC段是长为L的水平粗糙轨道,两段轨道相切于B点,一质量为m的滑块在小车上从A点静止开始沿轨道滑下,然后滑入BC轨道,最后恰好停在C点.已知小车质量M=3m,滑块与轨道BC间的动摩擦因数为μ,重力加速度为g.则
A.全程滑块水平方向相对地面的位移为R+L
B.全程小车相对地面的位移大小
C.最终小车和滑块一起向左运动
D.μ、L、R三者之间的关系为R=4μL
9.如图所示,带有半圆形槽的物块P,放在足够长的光滑水平地面上,一侧紧靠竖直墙壁.已知半圆形槽的半径为R,槽面光滑,a、c为槽的最高点,b为最低点.现让一小球Q(可视为质点),从a点正上方h处由静止释放,进入半圆形槽后刚好可以到达c点,则小球Q与物块P的质量之比为
A. B.
C. D.
10.如图所示,在光滑水平面上有两个滑块A和B(B的左侧连接轻弹簧),它们的质量分别为1kg和2kg。滑块A现以2m/s的速度向右运动,滑块B以3m/s的速度向左运动,若以水平向右方向为正方向,则下列说法正确的是( )
A.当滑块A的速度减为零时,弹簧被压缩到最短
B.当滑块A的速度为-6m/s时,滑块B的速度为1m/s
C.当两滑块相距最近时,弹簧弹性势能为
D.从开始到两滑块相距最近的过程中滑块A受到的冲量为
11.如图所示,A、B两小球质量分别为m1、m2,放在光滑的水平面上,水平面的右侧与竖直平面内一光滑曲面相切,现给A一向右的速度v0与B发生对心弹性碰撞,小球B沿曲面上升到最高点后又能再沿曲面滑回到水平面若要B返回水平面时能再与A发生碰撞,A、B的质量m1与m2应满足的关系是( )
A. B. C. D.
12.如图所示,足够长的木板静止在光滑水平面上,木板质量为M,质量为m的小木块静止在长木板_上,木板与小木块间的动摩擦因数为μ。现若给小木块向右的瞬间冲量为I,小木块在木板上留下划痕长为x1;若给小木块向右的瞬间冲量为2I,小木块在木板上留下划痕长为x2,则两次划痕长度之比为( )
A.1:2 B.1:4
C.1:8 D.M与m大小关系未知而无法确定
13.如图所示,质量分别为m和2m的A,B两个木块间用轻弹簧相连,放在光滑水平面上,A紧靠竖直墙壁.用水平力向左推B,将弹簧压缩,推到某位置静止时推力大小为F,弹簧的弹性势能为E,在此位置突然撤去推力,下列说法中正确的是( )
A.撤去推力的瞬间,B的加速度大小为
B.从撤去推力到A离开竖直墙壁前,A,B和弹簧组成的系统动量守恒,机械能守恒
C.A离开竖直墙壁后,弹簧弹性势能最大值为
D.A离开竖直墙壁后,弹簧弹性势能最大值为E
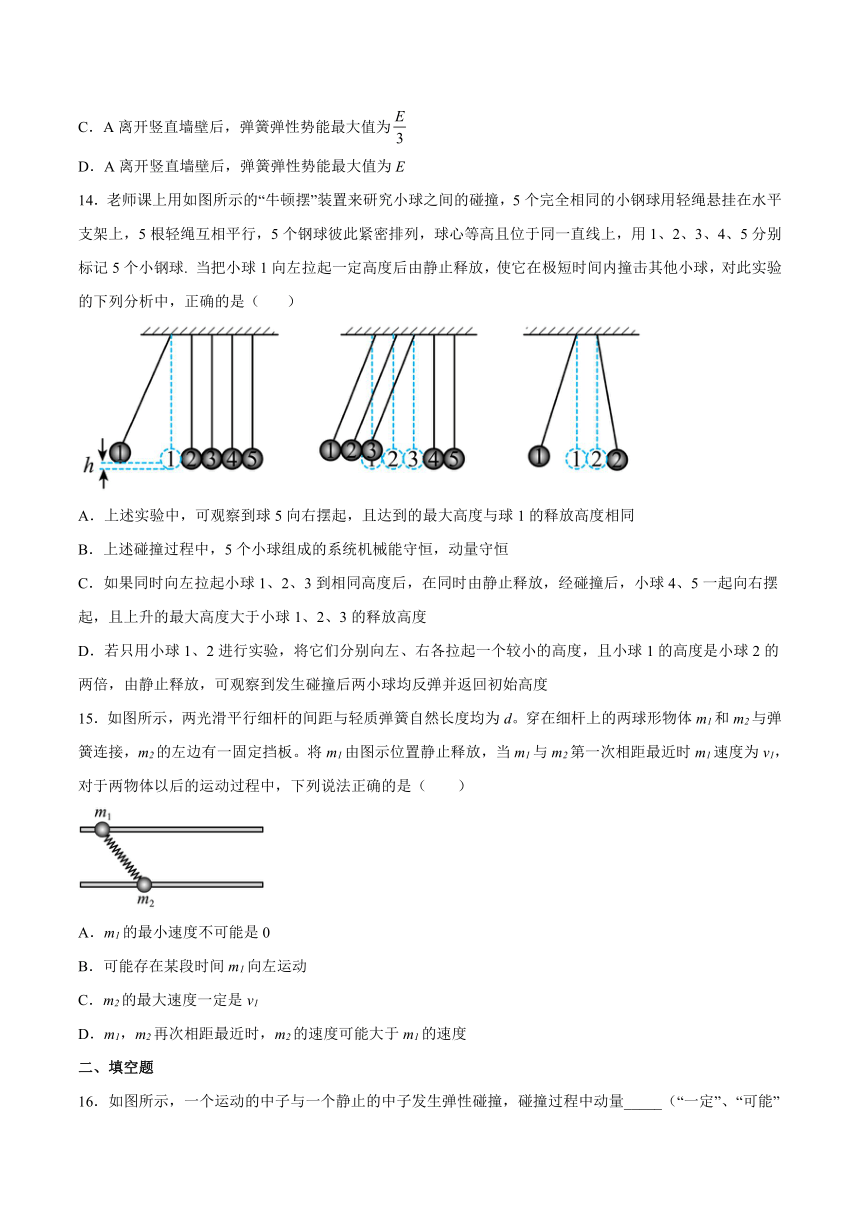
14.老师课上用如图所示的“牛顿摆”装置来研究小球之间的碰撞,5个完全相同的小钢球用轻绳悬挂在水平支架上,5根轻绳互相平行,5个钢球彼此紧密排列,球心等高且位于同一直线上,用1、2、3、4、5分别标记5个小钢球. 当把小球1向左拉起一定高度后由静止释放,使它在极短时间内撞击其他小球,对此实验的下列分析中,正确的是( )
A.上述实验中,可观察到球5向右摆起,且达到的最大高度与球1的释放高度相同
B.上述碰撞过程中,5个小球组成的系统机械能守恒,动量守恒
C.如果同时向左拉起小球1、2、3到相同高度后,在同时由静止释放,经碰撞后,小球4、5一起向右摆起,且上升的最大高度大于小球1、2、3的释放高度
D.若只用小球1、2进行实验,将它们分别向左、右各拉起一个较小的高度,且小球1的高度是小球2的两倍,由静止释放,可观察到发生碰撞后两小球均反弹并返回初始高度
15.如图所示,两光滑平行细杆的间距与轻质弹簧自然长度均为d。穿在细杆上的两球形物体m1和m2与弹簧连接,m2的左边有一固定挡板。将m1由图示位置静止释放,当m1与m2第一次相距最近时m1速度为v1,对于两物体以后的运动过程中,下列说法正确的是( )
A.m1的最小速度不可能是0
B.可能存在某段时间m1向左运动
C.m2的最大速度一定是v1
D.m1,m2再次相距最近时,m2的速度可能大于m1的速度
二、填空题
16.如图所示,一个运动的中子与一个静止的中子发生弹性碰撞,碰撞过程中动量_____(“一定”、“可能”或“一定不”)守恒,碰撞后A中子_____(“静止”“向右运动”或“向左运动”).
17.两小孩在冰面上乘坐“碰碰车”相向运动,A车总质量为50kg,以2m/s的速度向右运动;B车总质量为70kg,以3m/s的速度向左运动,碰撞后,A以1.5m/s的速度向左运动,则B的速度大小为_____m/s,方向向_____(选填“左”或“右”),该碰撞是_____(选填“弹性“或“非弹性”)碰撞
18.如图所示,两个半径为R的光滑圆弧轨道AB、EF固定在地面上,一质量为m的小物体(可看成质点)从轨道的最高点A处由静止滑下,质量为m、长为R的小车静止在光滑的水平面CD上,小车平面与光滑圆弧轨道末端BE齐平。物体从轨道末端的B滑上小车,小车即向右运动,当小车右端与壁DE刚接触时,物体恰好滑到小车的右端且相对小车静止。重力加速度为g,则:
(1)物体从A处滑到B处时的速度大小为______;
(2)物体滑到小车右端时的速度大小为______;
小车与DE相碰后立即停止运动,但与DE不粘连,物体则继续滑上光滑轨道EF,以后又滑下来冲上小车。求:
(3)物体滑上EF轨道的最高点P相对于E点的高度h=______;
(4)水平面CD的长度L=______;
(5)当物体再从EF上滑下并滑上小车,如果小车与壁BC相碰后速度也立即变为零,最后物体停在小车上的Q点。则可知Q点距小车的右端距离为______。
19.如图所示,光滑水平面上用轻绳连接质量分别为和的两个物体和B,物体静止,物体B以初速度水平向右运动,绳子被拉紧时突然断裂,物体B的速度变为,则物体的速度变为______。根据以上数据______求出此过程中系统损失的机械能(选填“能”或“不能”)。
三、综合题
20.质量为2 kg的小球A在光滑水平面上以6 m/s 的速度向右运动,恰遇上质量为5 kg、以4 m/s的速度向左运动的小球B,碰撞后B球恰好静止,求碰撞后A球的速度。
21.如图所示,一长度为L的轻绳,一端固定一个质量为m的小球a,另一端固定在O点,O点距离地面的高度也为L,在O点正下方距离O点处有一光滑小铁钉c,c的正下方放有小球b。初始小球a与O点在同一水平线上,轻绳伸直。现由静止释放小球a,小球a与小球b碰后粘在一起并向左摆动,恰好能够沿圆弧运动到c点正上方。小球a和小球b均可视为质点,重力加速度为g,空气阻力不计。求:
(1)碰后瞬间小球a的速度大小;
(2)小球b的质量。
22.如图所示,光滑水平面左端接一竖直光滑半圆轨道,轨道半径R=1.6m,右端接一斜面,斜面的倾角θ=37°,一质量为m的物块甲从斜面上离水平面高度h=3R为的A点由静止滑下,刚好能到达半圆轨道的最高点E点,已知sin37°=0.6,cos37°=0.8,g=10m/s2.
(1)求物块甲与斜面间的动摩擦因数;
(2)如果在水平面上C点放一材质与物块甲相同、质量为的物块乙,物块甲从斜面上滑下后与物块乙发生弹性碰撞,碰后物块乙恰好能到达半圆轨道的最高点E,则物块甲下滑时的高度为多少?
23.如图所示,现有一游戏滑道模拟装置固定在地面上,该装置竖直放置,由AB、BC、CD三部分组成,AB与BC两轨道平滑连接,CD为半圆弯管轨道。现将1号球从AB轨道上的P点静止释放,其下滑到最低点与静止在B点的2号球发生弹性碰撞,2号球通过弯管后从D点抛出,恰好落在B点。已知两球质量均为m=1kg,水平轨道BC长度L=1.6m,弯管半径R=0.4m,重力加速度g=10m/s2(小球可看成质点,半圆弯管内径略大于小球直径,不计一切摩擦)求:
(1)2号球运动到D点时对管壁的作用力F;
(2)P点距水平轨道BC的竖直高度H。
试卷第1页,共3页
参考答案:
1.D
【详解】
根据动量守恒定律得:p1+p2=p1′+p2′
解得:p1′=2kg m/s.
碰撞过程系统的总动能不增加,则有:
代入数据解得: .
碰撞后甲的速度不大于乙的速度,则有:
代入数据解得:.
综上有 ,故D正确,ABC错误.故选D.
点睛:对于碰撞过程,往往根据三大规律,分析两个质量的范围:1、动量守恒;2、总动能不增加;3、碰撞后两物体同向运动时,后面物体的速度不大于前面物体的速度.
2.B
【详解】
两球碰撞过程系统动量守恒,以A的初速度方向为正方向,由动量守恒定律得
又没有机械能损失,根据机械能守恒定律得
带入数据解得
故B正确,ACD错误。
故选B。
3.B
【详解】
两球不发生接触的临界条件
v1=v2
由动量守恒定律
由能量关系
联立解得
故选B。
4.B
【详解】
AB.小球A、B在水平方向上,系统无水平方向外力,内力为弹簧弹力,则对球A、B、弹簧系统水平方向动量守恒,机械能守恒,则有
为弹簧伸长量,当两球速度相等时,相距最远,由动量守恒可知,此时
A错误,B正确;
C.若B的速度为零,则有
此时弹簧恢复为原长,则第二次恢复原长的过程中,A一直加速,B一直减速,有
C错误;
D.当相距最远时,A、B的速度相等,系统的动能不为零,若为零,则不满足动量守恒,D错误
故选B。
5.D
【详解】
A.物块C与物块B碰撞时动量守恒,有
①
解得碰后速度为
②
故A错误;
B.物块C与物块B碰撞过程中损失的机械能为
③
故B错误;
D.若滑环A不固定,物块C与物块B粘在一起后,相对于A做曲线运动,会向右拉动A一起运动,当A、B、C三者水平方向速度相等(设为v2)时,B、C摆起的高度最大(设为h),根据动量守恒定律和能量守恒定律有
④
⑤
联立②④⑤解得
⑥
故D正确;
C.当滑环A所受合外力为零时速度达到最大(设为v3),易知此时B、C整体恰好摆回至最低点,设此时B、C整体的速度为v4,根据动量守恒定律和能量守恒定律有
⑦
⑧
联立②⑦⑧解得
⑨
故C错误。
故选D。
6.D
【详解】
A.由图示图象可知,B的加速度:,负号表示加速度的方向,由牛顿第二定律得:,代入解得,,故A错误;
BD.由图示图象可知,木板获得的速度为,A、B组成的系统动量守恒,以B的初速度方向为正方向,由动量守恒定律得:,解得木板A的质量为,木板获得的动能为:
系统损失的机械能为,故B错误,D正确;
C.由图得到:内B的位移为
A的位移为,木板A的最小长度为,故C错误.
7.C
【详解】
设第一次滑块离开时木板速度为v,选v0的方向为正,由系统的动量守恒,有
设滑块与木板间摩擦力为f,木板长L,滑行距离s,则: 由动能定理对木板
对滑块
即
当板固定时
解得
v3=4m/s
故C正确ABD错误。
故选C。
8.B
【详解】
设全程小车相对地面的位移大小为s,则滑块水平方向相对地面的位移 x=R+L-s,选项A错误.取水平向右为正方向,由水平动量守恒得:,即,结合M=3m,解得 s=(R+L),x=(R+L).故B正确.对整个过程,由动量守恒定律得:0=(m+M)v′,得v′=0则最终小车和滑块静止,选项C错误;由能量守恒定律得 mgR=μmgL,得 R=μL,故D错误.
9.B
【详解】
小球从开始下落到到达b点的过程中,槽静止不动,此时:;当小球向上运动到达c点时球和槽共速,由动量守恒:;由能量关系: ,联立解得;
A. ,与结论不相符,选项A错误;
B. ,与结论相符,选项B正确;
C. ,与结论不相符,选项C错误;
D. ,与结论不相符,选项D错误;
10.C
【详解】
AC.当滑块A、B的速度相同时,间距最小,弹簧压缩量最大,此时速度为v,根据动量守恒,以向右为正方向
解得
根据能量守恒
A错误C正确;
B.滑块A和B碰前的总能量为
当滑块A的速度为-6m/s时,滑块B的速度为1m/s时,总的能量为
能量不能增加,B错误;
D.从开始到两滑块相距最近的过程中,根据动量定理
D错误。
故选C。
11.A
【详解】
当A与B发生碰撞时,由动量守恒定律得
由于A与B发生对心弹性碰撞,根据机械能定律得
解得
显然,如果二者碰撞后都向右运动或A停止运动,是一定能发生二次碰撞的,在碰撞后A向左运动时,要能发生二次碰撞,需有
解得
BCD错误,A正确。
故选A。
12.B
【详解】
对木块,由动量定理得
对木板和木块整体分析,由动量守恒定律得
由功能关系得
联立解得
故ACD错,B对。
故选B。
13.AC
【详解】
A.撤去F后,B水平方向受到弹簧的弹力F,根据牛顿第二定律
A正确;
B.A离开竖直墙前,竖直方向两物体的重力与水平面的支持力平衡,合力为零,而墙对A有向右的弹力,系统水平方向的合外力不为零,动量不守恒。这个过程中,只有弹簧的弹力对B做功,系统的机械能守恒,B错误;
CD.当弹簧恢复原长时,A开始离开竖直墙,系统水平方向不受外力,竖直方向外力平衡,则系统的动量守恒,只有弹簧的弹力做功,机械能也守恒。当两物体速度相同时,弹簧伸长最长或压缩最短,弹性势能最大,设两物体相同速度为v,A离开墙时,B的速度为,根据动量守恒和机械能守恒得
又因为在A离开竖墙之前,弹簧弹性势能全部转化为B的动能
联立解得
C正确,D错误。
故选AC。
14.AB
【详解】
A. 上述实验中,由于5个球是完全相同的小球,则相互碰撞时要交换速度,即第5个球被碰瞬时的速度等于第1个球刚要与2球碰撞时的速度,由能量关系可知,观察到球5向右摆起,且达到的最大高度与球1的释放高度相同,选项A正确;
B. 上述碰撞过程中,5个小球组成的系统碰撞过程无能量损失,则机械能守恒,水平方向受合外力为零,则系统的动量守恒,选项B正确;
C. 如果同时向左拉起小球1、2、3到相同高度同时由静止释放,则3与4碰后,3停止4具有向右的速度,4与5碰撞交换速度,4停止5向右摆起;3刚停止的时候2球过来与之碰撞交换速度,然后3与4碰撞,使4向右摆起;2球刚停止的时候1球过来与之碰撞交换速度,然后2与3碰撞交换速度,使3向右摆起;故经碰撞后,小球3、4、5一起向右摆起,且上升的最大高度与小球1、2、3的释放高度相同;故C错误;
D. 若只用小球1、2进行实验,将它们分别向左、右各拉起一个较小的高度,且小球1的高度是小球2的两倍,由静止释放,则到达最低点时1球的速度是2球的两倍,相碰后两球交换速度各自反弹,则可观察到发生碰撞后小球2的高度是小球1的两倍,选项D错误.
15.BD
【详解】
当m1与m2第一次相距最近后,m2开始离开挡板,m1向右运动,弹簧被拉长,m2在弹簧弹力作用下向右运动,m1减速,m2加速,达到共同速度时两者相距最远,此后m1继续减速,m2加速,当两球再次相距最近时,m1达到最小速度,m2达最大速度,两球组成的系统在水平方向所受合外力为零,系统在水平方向动量守恒,以向右为正方向,由动量守恒定律得
由机械能守恒定律得
解得
A.当m1=m2时m1的最小速度为0,A错误;
B.如果m1<m2,则v1′<0,即m1的速度向左,由此可知,可能存在某段时间m1向左运动,B正确;
C.由于两球的速度不一定相等,由v2v1可知,m2的最大速度不一定是v1,C错误;
D.当m1>m2时,m1、m2再次相距最近时,m2的速度可能大于m1的速度,D正确。
故选BD。
16. 一定 静止
【详解】
试题分析:考查动量守恒定理,应用动能定理分析解决.
解:一个运动的中子与一个静止的中子发生弹性碰撞,由动量守恒定理可得:碰撞过程中动量是守恒的.
因为发生的是弹性碰撞,且两个中子质量是一样的,所以运动的A中子的能量无损失的传递给B中子,故碰撞后:A静止,B速度与A原来的速度相等.
故答案为一定,静止.
17. 0.5, 左, 非弹性.
【详解】
第一空.A、B组成的系统动量守恒,以向左为正方向,由动量守恒定律得:
mBvB﹣mAvA=mAvA′+mBvB′,即:70×3﹣50×2=50×1.5+70vB′,
解得:vB′=0.5m/s
第二空. 方向:水平向左;
第三空.碰撞前的能量为:
碰撞后的能量为:
综上所述,碰撞前后的能量不守恒,故为非弹性碰撞.
18.
【详解】
(1)物体从A处滑到B处,由机械能守恒得
mgR=
物体滑到B点时速度大小为
(2)因为物体滑到小车右端时,恰好与小车共速,取水平向右为正方向,由动量守恒定律得
mv=2mv'
故
(3)物体滑上高为h的高度后速度为0,物体在EF轨道上上滑过程,由机械能守恒得
解得
h=R
(4)设物块与小车间的摩擦力为F,小车从C到D的过程,对物块来说,它做减速运动,根据动能定理得
对小车来说,它做加速运动,则根据动能定理得
二式相减得
,
(5)物块从EF上滑下时,速度的大小也是v',它与小车相互作用仍然能达到共速,设共速的大小为v″,取向左为正方向,根据动量守恒得
mv'=2mv″
则
v″=v'=v
设物块在小车上滑行的距离为x1,则根据能量守恒得
解得
当小车停止时,物块的速度为v″,设它向前滑行的距离为x2后停止下来,则由动能定理得
解得
所以Q点距小车的右端距离为
19. 能
【详解】
物体和B在光滑水平面上运动,动量守恒,有
解得
根据能量守恒可知此过程中系统损失的机械能
代入和可得到,因此根据以上数据能求出此过程中系统损失的机械能。
20.
【详解】
规定向右为正方向,由动量守恒定律可得
代入数据解得
方向向左
21.(1);(2)
【详解】
(1)设小球b的质量为,碰后整体恰运动到最高点,整体做圆周运动的半径为
根据牛顿第二定律有
设碰后小球a的速度为,碰后整体由最低点到最高点的过程,根据机械能守恒有
解得
(2)小球a由静止释放到最低点,根据机械能守恒有
小球a与小球b发生碰撞,根据动量守恒有
解得
22.(1);(2) 2.7m
【详解】
(1)根据牛顿第二定律得,mg=m,解得vE=,
对全过程运用动能定理得,mgh-2mgR-μmgcosθ =
h=3R
解得:μ=
(2)设物块乙在C点碰后的速度为v1,碰前甲的速度为v甲,碰后甲的速度为v2
物块乙恰好到达E点,根据机械能守恒定律得:mg 2R+=
解得:v1=
根据动量守恒定律和机械能守恒定律有:
mv甲=mv2+mv1
=+
解得:v甲=
设物块甲开始下滑的高度为H,
根据动能定理得:mgH-μmgcosθ =
解得:H=2.7m
23.(1)30N,方向竖直向上;(2)H=1.6m
【详解】
由题意可知小球离开轨道后在空中做平抛运动,设小球在空中运动时间为t,
根据小球水平方向做匀速直线运动可得
解得
vD=4m/s
根据D点受力情况可知
解得
F=30N
由牛顿第三定律小球对上管壁的压力为30N,方向竖直向上。
(2)由能量守恒
解得
v2=vC=4m/s
1号球和2号球发生弹性碰撞,则有
解得
v0=4m/s
解得
H=1.6m
答案第1页,共2页
一、选择题(共15题)
1.甲乙两球在水平光滑轨道上向同一方向运动,已知它们的动量分别是p1= 5kgm/s,p2=7kgm/s,甲从后面追上乙并且发生碰撞,碰后乙球的动量变为 10kgm/s.则二球质量m1和m2间的关系可以是下面的哪几种( )
A.m2=m1 B.m2=6m1 C.m2=2m1 D.m2=3m1
2.一个质量为m的小球A在光滑的水平面上以3m/s速度向右运动,与一个质量为2m的静止的小球B发生正碰,假设碰撞过程中没有机械能损失,则碰后( )
A.A球、B球都向右运动,速度都是1m/s
B.A球向左运动,速度为1m/s;B球向右运动,速度为2m/s
C.A球向左运动,速度为5m/s;B球向右运动,速度为1m/s
D.A球向右运动,速度为0.5m/s;B球向右运动,速度为1.25m/s
3.在光滑水平轨道上有两个小球A和B(均可看做质点),质量分别为2m和3m当两球间的距离大于L时,两球之间无相互作用;当两球间的距离等于或小于L时,两球间存在大小为F的恒定斥力,设A球从距离B球足够远处以某一初速度沿两球连线向原来静止的B球运动,如图所示,结果两球恰好接触,则该初速度大小为( )
A. B. C. D.
4.如图所示,足够长的两根光滑细杆水平平行放置(处在竖直面内),质量相等的两个小球A、B分别套在两杆上,开始时AB位置连线与杆垂直,A和B连接着一轻质弹簧,此时弹簧恰好为原长(弹簧永远在弹性限度内),现给B球一个初速度v0向右运动,则关于两小球的运动情况,下列说法正确的是( )
A.第一次两球相距最远时,B球的速度为0 B.第一次两球相距最远时,B球的速度为
C.从B球开始运动后,B球的速度不可能为零 D.第一次两球相距最远时,弹性势能最大,系统动能为0
5.如图所示,光滑的水平杆上有一质量为的滑环A,滑环上通过一根不可伸缩的轻绳悬挂着一个质量为的物块B(可视为质点),物块B恰好与光滑的水平面接触。质量为物块C(可视为质点)以速度冲向物块B,物块C与物块B碰后粘在一起向右运动,已知重力加速度为,则下列说法正确的是( )
A.物块C与物块B碰后速度为
B.物块C与物块B碰撞过程中损失的机械能为
C.若滑环A不固定,则滑环A最大速度为
D.若滑环A不固定,则物块B、C摆起的最大高度为
6.如图所示,长木板A放在光滑的水平面上,质量为m=2kg的另一物体B以水平速度滑上原来静止的长木板A的表面,由于A、B间存在摩擦,之后A、B速度随时间变化情况如图所示,下列说法正确的是
A.A、B间的动摩擦因数为0.2
B.系统损失的机械能为4J
C.木板A的最小长度为1.5m
D.木板获得的动能为1J
7.一质量为4kg的长木板,静止放在光滑的水平面上.一质量为3kg的滑块以6m/s水平速度从长木板的一端开始滑动,直到离开长木板,滑块刚离开长木板时的速度大小为2m/s。若将此长木板固定在水平桌面上,其他条件相同,则滑块离开长木板时的速度大小为( )
A.2m/s B.3m/s C.4m/s D.5m/s
8.如图,质量为M的小车静止在光滑的水平面上,小车AB段是半径为R的四分之一光滑圆弧轨道,BC段是长为L的水平粗糙轨道,两段轨道相切于B点,一质量为m的滑块在小车上从A点静止开始沿轨道滑下,然后滑入BC轨道,最后恰好停在C点.已知小车质量M=3m,滑块与轨道BC间的动摩擦因数为μ,重力加速度为g.则
A.全程滑块水平方向相对地面的位移为R+L
B.全程小车相对地面的位移大小
C.最终小车和滑块一起向左运动
D.μ、L、R三者之间的关系为R=4μL
9.如图所示,带有半圆形槽的物块P,放在足够长的光滑水平地面上,一侧紧靠竖直墙壁.已知半圆形槽的半径为R,槽面光滑,a、c为槽的最高点,b为最低点.现让一小球Q(可视为质点),从a点正上方h处由静止释放,进入半圆形槽后刚好可以到达c点,则小球Q与物块P的质量之比为
A. B.
C. D.
10.如图所示,在光滑水平面上有两个滑块A和B(B的左侧连接轻弹簧),它们的质量分别为1kg和2kg。滑块A现以2m/s的速度向右运动,滑块B以3m/s的速度向左运动,若以水平向右方向为正方向,则下列说法正确的是( )
A.当滑块A的速度减为零时,弹簧被压缩到最短
B.当滑块A的速度为-6m/s时,滑块B的速度为1m/s
C.当两滑块相距最近时,弹簧弹性势能为
D.从开始到两滑块相距最近的过程中滑块A受到的冲量为
11.如图所示,A、B两小球质量分别为m1、m2,放在光滑的水平面上,水平面的右侧与竖直平面内一光滑曲面相切,现给A一向右的速度v0与B发生对心弹性碰撞,小球B沿曲面上升到最高点后又能再沿曲面滑回到水平面若要B返回水平面时能再与A发生碰撞,A、B的质量m1与m2应满足的关系是( )
A. B. C. D.
12.如图所示,足够长的木板静止在光滑水平面上,木板质量为M,质量为m的小木块静止在长木板_上,木板与小木块间的动摩擦因数为μ。现若给小木块向右的瞬间冲量为I,小木块在木板上留下划痕长为x1;若给小木块向右的瞬间冲量为2I,小木块在木板上留下划痕长为x2,则两次划痕长度之比为( )
A.1:2 B.1:4
C.1:8 D.M与m大小关系未知而无法确定
13.如图所示,质量分别为m和2m的A,B两个木块间用轻弹簧相连,放在光滑水平面上,A紧靠竖直墙壁.用水平力向左推B,将弹簧压缩,推到某位置静止时推力大小为F,弹簧的弹性势能为E,在此位置突然撤去推力,下列说法中正确的是( )
A.撤去推力的瞬间,B的加速度大小为
B.从撤去推力到A离开竖直墙壁前,A,B和弹簧组成的系统动量守恒,机械能守恒
C.A离开竖直墙壁后,弹簧弹性势能最大值为
D.A离开竖直墙壁后,弹簧弹性势能最大值为E
14.老师课上用如图所示的“牛顿摆”装置来研究小球之间的碰撞,5个完全相同的小钢球用轻绳悬挂在水平支架上,5根轻绳互相平行,5个钢球彼此紧密排列,球心等高且位于同一直线上,用1、2、3、4、5分别标记5个小钢球. 当把小球1向左拉起一定高度后由静止释放,使它在极短时间内撞击其他小球,对此实验的下列分析中,正确的是( )
A.上述实验中,可观察到球5向右摆起,且达到的最大高度与球1的释放高度相同
B.上述碰撞过程中,5个小球组成的系统机械能守恒,动量守恒
C.如果同时向左拉起小球1、2、3到相同高度后,在同时由静止释放,经碰撞后,小球4、5一起向右摆起,且上升的最大高度大于小球1、2、3的释放高度
D.若只用小球1、2进行实验,将它们分别向左、右各拉起一个较小的高度,且小球1的高度是小球2的两倍,由静止释放,可观察到发生碰撞后两小球均反弹并返回初始高度
15.如图所示,两光滑平行细杆的间距与轻质弹簧自然长度均为d。穿在细杆上的两球形物体m1和m2与弹簧连接,m2的左边有一固定挡板。将m1由图示位置静止释放,当m1与m2第一次相距最近时m1速度为v1,对于两物体以后的运动过程中,下列说法正确的是( )
A.m1的最小速度不可能是0
B.可能存在某段时间m1向左运动
C.m2的最大速度一定是v1
D.m1,m2再次相距最近时,m2的速度可能大于m1的速度
二、填空题
16.如图所示,一个运动的中子与一个静止的中子发生弹性碰撞,碰撞过程中动量_____(“一定”、“可能”或“一定不”)守恒,碰撞后A中子_____(“静止”“向右运动”或“向左运动”).
17.两小孩在冰面上乘坐“碰碰车”相向运动,A车总质量为50kg,以2m/s的速度向右运动;B车总质量为70kg,以3m/s的速度向左运动,碰撞后,A以1.5m/s的速度向左运动,则B的速度大小为_____m/s,方向向_____(选填“左”或“右”),该碰撞是_____(选填“弹性“或“非弹性”)碰撞
18.如图所示,两个半径为R的光滑圆弧轨道AB、EF固定在地面上,一质量为m的小物体(可看成质点)从轨道的最高点A处由静止滑下,质量为m、长为R的小车静止在光滑的水平面CD上,小车平面与光滑圆弧轨道末端BE齐平。物体从轨道末端的B滑上小车,小车即向右运动,当小车右端与壁DE刚接触时,物体恰好滑到小车的右端且相对小车静止。重力加速度为g,则:
(1)物体从A处滑到B处时的速度大小为______;
(2)物体滑到小车右端时的速度大小为______;
小车与DE相碰后立即停止运动,但与DE不粘连,物体则继续滑上光滑轨道EF,以后又滑下来冲上小车。求:
(3)物体滑上EF轨道的最高点P相对于E点的高度h=______;
(4)水平面CD的长度L=______;
(5)当物体再从EF上滑下并滑上小车,如果小车与壁BC相碰后速度也立即变为零,最后物体停在小车上的Q点。则可知Q点距小车的右端距离为______。
19.如图所示,光滑水平面上用轻绳连接质量分别为和的两个物体和B,物体静止,物体B以初速度水平向右运动,绳子被拉紧时突然断裂,物体B的速度变为,则物体的速度变为______。根据以上数据______求出此过程中系统损失的机械能(选填“能”或“不能”)。
三、综合题
20.质量为2 kg的小球A在光滑水平面上以6 m/s 的速度向右运动,恰遇上质量为5 kg、以4 m/s的速度向左运动的小球B,碰撞后B球恰好静止,求碰撞后A球的速度。
21.如图所示,一长度为L的轻绳,一端固定一个质量为m的小球a,另一端固定在O点,O点距离地面的高度也为L,在O点正下方距离O点处有一光滑小铁钉c,c的正下方放有小球b。初始小球a与O点在同一水平线上,轻绳伸直。现由静止释放小球a,小球a与小球b碰后粘在一起并向左摆动,恰好能够沿圆弧运动到c点正上方。小球a和小球b均可视为质点,重力加速度为g,空气阻力不计。求:
(1)碰后瞬间小球a的速度大小;
(2)小球b的质量。
22.如图所示,光滑水平面左端接一竖直光滑半圆轨道,轨道半径R=1.6m,右端接一斜面,斜面的倾角θ=37°,一质量为m的物块甲从斜面上离水平面高度h=3R为的A点由静止滑下,刚好能到达半圆轨道的最高点E点,已知sin37°=0.6,cos37°=0.8,g=10m/s2.
(1)求物块甲与斜面间的动摩擦因数;
(2)如果在水平面上C点放一材质与物块甲相同、质量为的物块乙,物块甲从斜面上滑下后与物块乙发生弹性碰撞,碰后物块乙恰好能到达半圆轨道的最高点E,则物块甲下滑时的高度为多少?
23.如图所示,现有一游戏滑道模拟装置固定在地面上,该装置竖直放置,由AB、BC、CD三部分组成,AB与BC两轨道平滑连接,CD为半圆弯管轨道。现将1号球从AB轨道上的P点静止释放,其下滑到最低点与静止在B点的2号球发生弹性碰撞,2号球通过弯管后从D点抛出,恰好落在B点。已知两球质量均为m=1kg,水平轨道BC长度L=1.6m,弯管半径R=0.4m,重力加速度g=10m/s2(小球可看成质点,半圆弯管内径略大于小球直径,不计一切摩擦)求:
(1)2号球运动到D点时对管壁的作用力F;
(2)P点距水平轨道BC的竖直高度H。
试卷第1页,共3页
参考答案:
1.D
【详解】
根据动量守恒定律得:p1+p2=p1′+p2′
解得:p1′=2kg m/s.
碰撞过程系统的总动能不增加,则有:
代入数据解得: .
碰撞后甲的速度不大于乙的速度,则有:
代入数据解得:.
综上有 ,故D正确,ABC错误.故选D.
点睛:对于碰撞过程,往往根据三大规律,分析两个质量的范围:1、动量守恒;2、总动能不增加;3、碰撞后两物体同向运动时,后面物体的速度不大于前面物体的速度.
2.B
【详解】
两球碰撞过程系统动量守恒,以A的初速度方向为正方向,由动量守恒定律得
又没有机械能损失,根据机械能守恒定律得
带入数据解得
故B正确,ACD错误。
故选B。
3.B
【详解】
两球不发生接触的临界条件
v1=v2
由动量守恒定律
由能量关系
联立解得
故选B。
4.B
【详解】
AB.小球A、B在水平方向上,系统无水平方向外力,内力为弹簧弹力,则对球A、B、弹簧系统水平方向动量守恒,机械能守恒,则有
为弹簧伸长量,当两球速度相等时,相距最远,由动量守恒可知,此时
A错误,B正确;
C.若B的速度为零,则有
此时弹簧恢复为原长,则第二次恢复原长的过程中,A一直加速,B一直减速,有
C错误;
D.当相距最远时,A、B的速度相等,系统的动能不为零,若为零,则不满足动量守恒,D错误
故选B。
5.D
【详解】
A.物块C与物块B碰撞时动量守恒,有
①
解得碰后速度为
②
故A错误;
B.物块C与物块B碰撞过程中损失的机械能为
③
故B错误;
D.若滑环A不固定,物块C与物块B粘在一起后,相对于A做曲线运动,会向右拉动A一起运动,当A、B、C三者水平方向速度相等(设为v2)时,B、C摆起的高度最大(设为h),根据动量守恒定律和能量守恒定律有
④
⑤
联立②④⑤解得
⑥
故D正确;
C.当滑环A所受合外力为零时速度达到最大(设为v3),易知此时B、C整体恰好摆回至最低点,设此时B、C整体的速度为v4,根据动量守恒定律和能量守恒定律有
⑦
⑧
联立②⑦⑧解得
⑨
故C错误。
故选D。
6.D
【详解】
A.由图示图象可知,B的加速度:,负号表示加速度的方向,由牛顿第二定律得:,代入解得,,故A错误;
BD.由图示图象可知,木板获得的速度为,A、B组成的系统动量守恒,以B的初速度方向为正方向,由动量守恒定律得:,解得木板A的质量为,木板获得的动能为:
系统损失的机械能为,故B错误,D正确;
C.由图得到:内B的位移为
A的位移为,木板A的最小长度为,故C错误.
7.C
【详解】
设第一次滑块离开时木板速度为v,选v0的方向为正,由系统的动量守恒,有
设滑块与木板间摩擦力为f,木板长L,滑行距离s,则: 由动能定理对木板
对滑块
即
当板固定时
解得
v3=4m/s
故C正确ABD错误。
故选C。
8.B
【详解】
设全程小车相对地面的位移大小为s,则滑块水平方向相对地面的位移 x=R+L-s,选项A错误.取水平向右为正方向,由水平动量守恒得:,即,结合M=3m,解得 s=(R+L),x=(R+L).故B正确.对整个过程,由动量守恒定律得:0=(m+M)v′,得v′=0则最终小车和滑块静止,选项C错误;由能量守恒定律得 mgR=μmgL,得 R=μL,故D错误.
9.B
【详解】
小球从开始下落到到达b点的过程中,槽静止不动,此时:;当小球向上运动到达c点时球和槽共速,由动量守恒:;由能量关系: ,联立解得;
A. ,与结论不相符,选项A错误;
B. ,与结论相符,选项B正确;
C. ,与结论不相符,选项C错误;
D. ,与结论不相符,选项D错误;
10.C
【详解】
AC.当滑块A、B的速度相同时,间距最小,弹簧压缩量最大,此时速度为v,根据动量守恒,以向右为正方向
解得
根据能量守恒
A错误C正确;
B.滑块A和B碰前的总能量为
当滑块A的速度为-6m/s时,滑块B的速度为1m/s时,总的能量为
能量不能增加,B错误;
D.从开始到两滑块相距最近的过程中,根据动量定理
D错误。
故选C。
11.A
【详解】
当A与B发生碰撞时,由动量守恒定律得
由于A与B发生对心弹性碰撞,根据机械能定律得
解得
显然,如果二者碰撞后都向右运动或A停止运动,是一定能发生二次碰撞的,在碰撞后A向左运动时,要能发生二次碰撞,需有
解得
BCD错误,A正确。
故选A。
12.B
【详解】
对木块,由动量定理得
对木板和木块整体分析,由动量守恒定律得
由功能关系得
联立解得
故ACD错,B对。
故选B。
13.AC
【详解】
A.撤去F后,B水平方向受到弹簧的弹力F,根据牛顿第二定律
A正确;
B.A离开竖直墙前,竖直方向两物体的重力与水平面的支持力平衡,合力为零,而墙对A有向右的弹力,系统水平方向的合外力不为零,动量不守恒。这个过程中,只有弹簧的弹力对B做功,系统的机械能守恒,B错误;
CD.当弹簧恢复原长时,A开始离开竖直墙,系统水平方向不受外力,竖直方向外力平衡,则系统的动量守恒,只有弹簧的弹力做功,机械能也守恒。当两物体速度相同时,弹簧伸长最长或压缩最短,弹性势能最大,设两物体相同速度为v,A离开墙时,B的速度为,根据动量守恒和机械能守恒得
又因为在A离开竖墙之前,弹簧弹性势能全部转化为B的动能
联立解得
C正确,D错误。
故选AC。
14.AB
【详解】
A. 上述实验中,由于5个球是完全相同的小球,则相互碰撞时要交换速度,即第5个球被碰瞬时的速度等于第1个球刚要与2球碰撞时的速度,由能量关系可知,观察到球5向右摆起,且达到的最大高度与球1的释放高度相同,选项A正确;
B. 上述碰撞过程中,5个小球组成的系统碰撞过程无能量损失,则机械能守恒,水平方向受合外力为零,则系统的动量守恒,选项B正确;
C. 如果同时向左拉起小球1、2、3到相同高度同时由静止释放,则3与4碰后,3停止4具有向右的速度,4与5碰撞交换速度,4停止5向右摆起;3刚停止的时候2球过来与之碰撞交换速度,然后3与4碰撞,使4向右摆起;2球刚停止的时候1球过来与之碰撞交换速度,然后2与3碰撞交换速度,使3向右摆起;故经碰撞后,小球3、4、5一起向右摆起,且上升的最大高度与小球1、2、3的释放高度相同;故C错误;
D. 若只用小球1、2进行实验,将它们分别向左、右各拉起一个较小的高度,且小球1的高度是小球2的两倍,由静止释放,则到达最低点时1球的速度是2球的两倍,相碰后两球交换速度各自反弹,则可观察到发生碰撞后小球2的高度是小球1的两倍,选项D错误.
15.BD
【详解】
当m1与m2第一次相距最近后,m2开始离开挡板,m1向右运动,弹簧被拉长,m2在弹簧弹力作用下向右运动,m1减速,m2加速,达到共同速度时两者相距最远,此后m1继续减速,m2加速,当两球再次相距最近时,m1达到最小速度,m2达最大速度,两球组成的系统在水平方向所受合外力为零,系统在水平方向动量守恒,以向右为正方向,由动量守恒定律得
由机械能守恒定律得
解得
A.当m1=m2时m1的最小速度为0,A错误;
B.如果m1<m2,则v1′<0,即m1的速度向左,由此可知,可能存在某段时间m1向左运动,B正确;
C.由于两球的速度不一定相等,由v2v1可知,m2的最大速度不一定是v1,C错误;
D.当m1>m2时,m1、m2再次相距最近时,m2的速度可能大于m1的速度,D正确。
故选BD。
16. 一定 静止
【详解】
试题分析:考查动量守恒定理,应用动能定理分析解决.
解:一个运动的中子与一个静止的中子发生弹性碰撞,由动量守恒定理可得:碰撞过程中动量是守恒的.
因为发生的是弹性碰撞,且两个中子质量是一样的,所以运动的A中子的能量无损失的传递给B中子,故碰撞后:A静止,B速度与A原来的速度相等.
故答案为一定,静止.
17. 0.5, 左, 非弹性.
【详解】
第一空.A、B组成的系统动量守恒,以向左为正方向,由动量守恒定律得:
mBvB﹣mAvA=mAvA′+mBvB′,即:70×3﹣50×2=50×1.5+70vB′,
解得:vB′=0.5m/s
第二空. 方向:水平向左;
第三空.碰撞前的能量为:
碰撞后的能量为:
综上所述,碰撞前后的能量不守恒,故为非弹性碰撞.
18.
【详解】
(1)物体从A处滑到B处,由机械能守恒得
mgR=
物体滑到B点时速度大小为
(2)因为物体滑到小车右端时,恰好与小车共速,取水平向右为正方向,由动量守恒定律得
mv=2mv'
故
(3)物体滑上高为h的高度后速度为0,物体在EF轨道上上滑过程,由机械能守恒得
解得
h=R
(4)设物块与小车间的摩擦力为F,小车从C到D的过程,对物块来说,它做减速运动,根据动能定理得
对小车来说,它做加速运动,则根据动能定理得
二式相减得
,
(5)物块从EF上滑下时,速度的大小也是v',它与小车相互作用仍然能达到共速,设共速的大小为v″,取向左为正方向,根据动量守恒得
mv'=2mv″
则
v″=v'=v
设物块在小车上滑行的距离为x1,则根据能量守恒得
解得
当小车停止时,物块的速度为v″,设它向前滑行的距离为x2后停止下来,则由动能定理得
解得
所以Q点距小车的右端距离为
19. 能
【详解】
物体和B在光滑水平面上运动,动量守恒,有
解得
根据能量守恒可知此过程中系统损失的机械能
代入和可得到,因此根据以上数据能求出此过程中系统损失的机械能。
20.
【详解】
规定向右为正方向,由动量守恒定律可得
代入数据解得
方向向左
21.(1);(2)
【详解】
(1)设小球b的质量为,碰后整体恰运动到最高点,整体做圆周运动的半径为
根据牛顿第二定律有
设碰后小球a的速度为,碰后整体由最低点到最高点的过程,根据机械能守恒有
解得
(2)小球a由静止释放到最低点,根据机械能守恒有
小球a与小球b发生碰撞,根据动量守恒有
解得
22.(1);(2) 2.7m
【详解】
(1)根据牛顿第二定律得,mg=m,解得vE=,
对全过程运用动能定理得,mgh-2mgR-μmgcosθ =
h=3R
解得:μ=
(2)设物块乙在C点碰后的速度为v1,碰前甲的速度为v甲,碰后甲的速度为v2
物块乙恰好到达E点,根据机械能守恒定律得:mg 2R+=
解得:v1=
根据动量守恒定律和机械能守恒定律有:
mv甲=mv2+mv1
=+
解得:v甲=
设物块甲开始下滑的高度为H,
根据动能定理得:mgH-μmgcosθ =
解得:H=2.7m
23.(1)30N,方向竖直向上;(2)H=1.6m
【详解】
由题意可知小球离开轨道后在空中做平抛运动,设小球在空中运动时间为t,
根据小球水平方向做匀速直线运动可得
解得
vD=4m/s
根据D点受力情况可知
解得
F=30N
由牛顿第三定律小球对上管壁的压力为30N,方向竖直向上。
(2)由能量守恒
解得
v2=vC=4m/s
1号球和2号球发生弹性碰撞,则有
解得
v0=4m/s
解得
H=1.6m
答案第1页,共2页
同课章节目录
- 第1章 碰撞与动量守恒
- 1.1 动量变化与冲量的关系
- 1.2 动量守恒定律
- 1.3 动量守恒定律的案例分析
- 1.4 美妙的守恒定律
- 第2章 机械振动
- 2.1 简谐运动
- 2.2 物体做简谐运动的原因
- 2.3 摆钟的物理原理
- 2.4 单摆振动的周期
- 2.5 受迫振动与共振
- 第3章 机械波
- 3.1 机械波的产生
- 3.2 机械波的描述
- 3.3 机械波案例分析
- 3.4 惠更斯原理 波的反射与折射
- 3.5 波的干涉与衍射
- 3.6 多普勒效应
- 第4章 光及其应用
- 4.1 光的折射
- 4.2 全反射与光导纤维
- 4.3 光的干涉
- 4.4 用双缝干涉仪测量光的波长
- 4.5 光的衍射
- 4.6 光的偏振与立体电影
- 4.7 激光
