人教版八年级数学 下册 18.1.1平行四边形的性质(第一课时)(共15张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 18.1.1平行四边形的性质(第一课时)(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 16:20:14 | ||
图片预览

文档简介
(共15张PPT)
18.1.1 平行四边形的性质
人教版八年级数学下册
(第一课时)
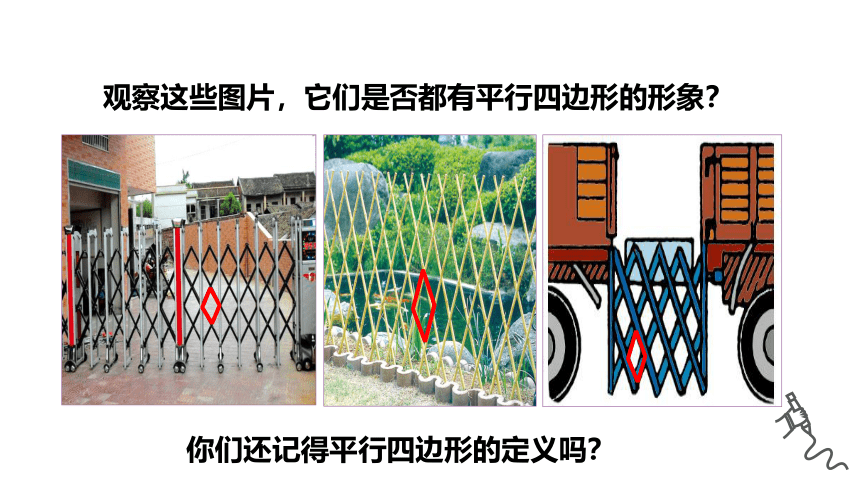
观察这些图片,它们是否都有平行四边形的形象?
你们还记得平行四边形的定义吗?
A
D
C
B
ABCD
平行四边形ABCD
平行四边形中相对的边称为 ,
平行四边形中相对的角称为 .
平行四边形中相邻的边称为 ,
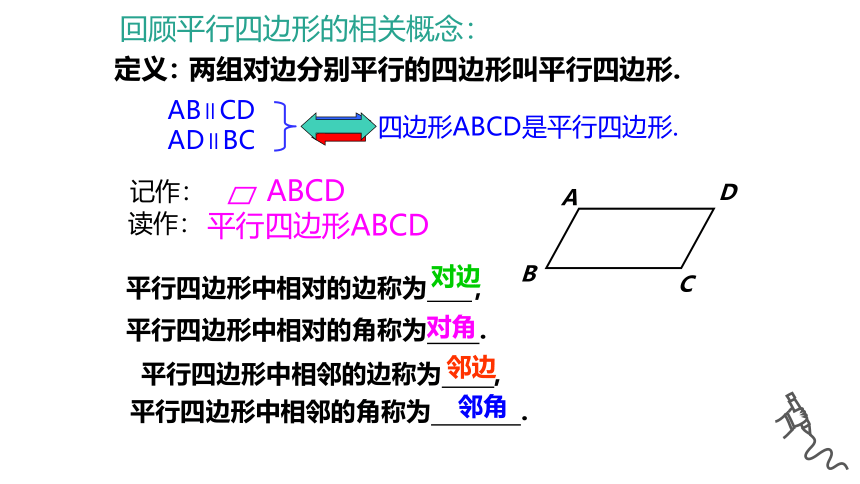
回顾平行四边形的相关概念:
定义:
两组对边分别平行的四边形叫平行四边形.
AB∥CD
AD∥BC
四边形ABCD是平行四边形.
记作:
读作:
对边
对角
邻边
邻角
平行四边形中相邻的角称为 .
平行四边形的边、角有怎样的数量关系?
A
D
C
B
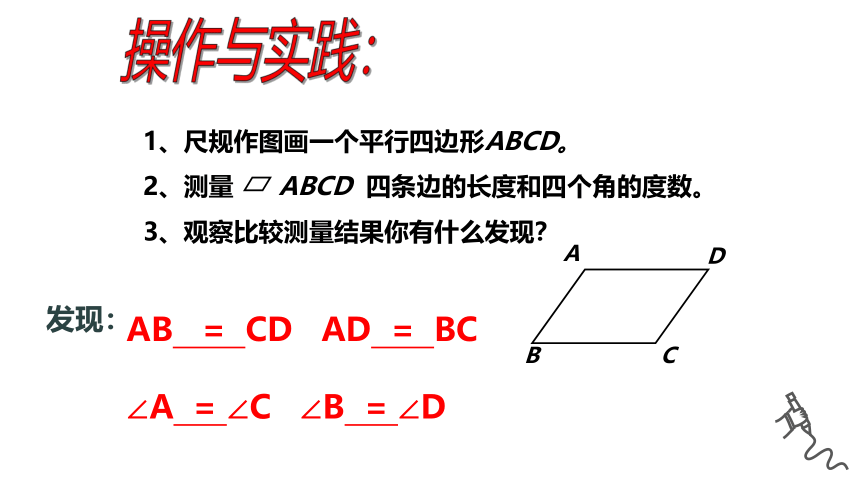
1、尺规作图画一个平行四边形ABCD。
2、测量 ABCD 四条边的长度和四个角的度数。
3、观察比较测量结果你有什么发现?
AB = CD AD = BC
∠A = ∠C ∠B = ∠D
A
D
C
B
发现:
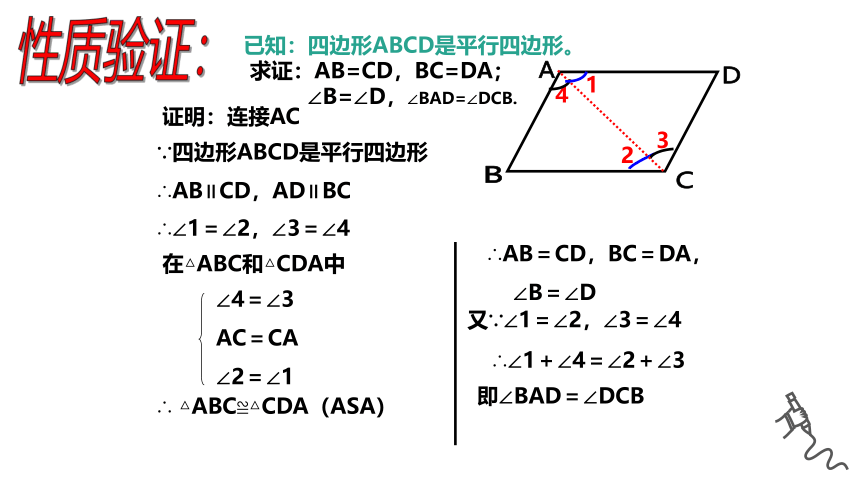
求证:AB=CD,BC=DA;
∠B=∠D,∠BAD=∠DCB.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠4=∠3
AC=CA
∠2=∠1
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
已知:四边形ABCD是平行四边形。
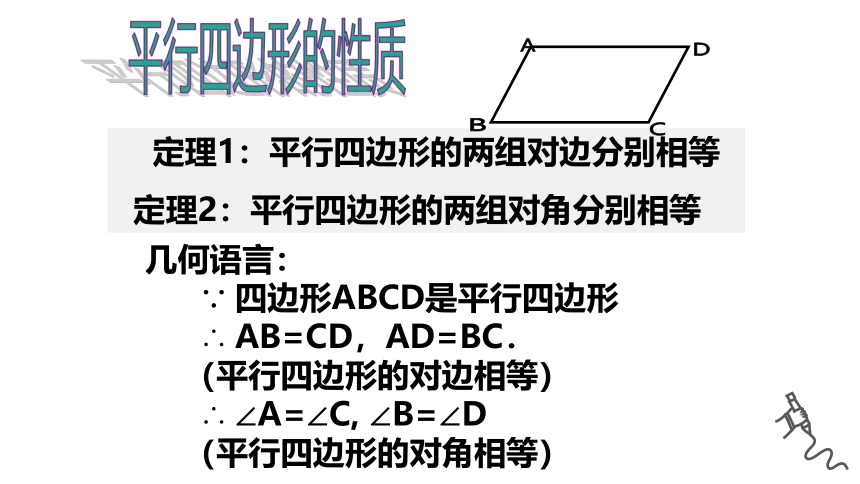
几何语言:
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.
(平行四边形的对边相等)
∴ ∠A=∠C, ∠B=∠D
(平行四边形的对角相等)
定理1:平行四边形的两组对边分别相等
定理2:平行四边形的两组对角分别相等
例1、如图 ,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
A
C
B
D
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又∵AB+BC+CD+AD=36,
∴ AD=BC=10m
例2 :已知在 ABCD中,AB=6cm,BC=4cm,求 ABCD 的周长。
A
B
C
D
连结AC,已知 ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴C ABCD=AB+CD+BC+AD=6+6+4+4=20(cm)
例3:平行四边形ABCD中,AE⊥BC于E,CF ⊥AD于F,求证:BE=DF.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D.
又∵ AE⊥BC于E,CF ⊥AD于F,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS),
∴BE=DF.
1.在□ ABCD中,∠A:∠B=1:2,则∠A= _____ ,∠B= ______,∠C= ______, ∠D= _______.
2.已知□ ABCD的周长为30cm,且AD-AB=1cm,则 BC= ______,CD= ______ .
8cm
7cm
60°
120°
120°
60°
反馈检测
3.如图,四边形ABCD是平行四边形,则
∠A:∠B :∠C: ∠D的值可以是( )。
A: 1:2:3:4 B:1:2:2:1
C: 2:2:1:1 D: 1:2:1:2
D
A
D
C
B
4.已知, ABCD 的周长为100 cm,两邻边之差为30cm,求 ABCD较短边的长。
反馈检测
课堂小结 :
1、定义:两组对边分别平行的四边形叫做平行四边形.
2、性质:平行四边形的对边平行且相等.
平行四边形的对角相等,邻角互补.
3、数学思想:转化思想.
作 业
习题18.1:
必做题:第1题、第2题
选做题:第8题。
18.1.1 平行四边形的性质
人教版八年级数学下册
(第一课时)
观察这些图片,它们是否都有平行四边形的形象?
你们还记得平行四边形的定义吗?
A
D
C
B
ABCD
平行四边形ABCD
平行四边形中相对的边称为 ,
平行四边形中相对的角称为 .
平行四边形中相邻的边称为 ,
回顾平行四边形的相关概念:
定义:
两组对边分别平行的四边形叫平行四边形.
AB∥CD
AD∥BC
四边形ABCD是平行四边形.
记作:
读作:
对边
对角
邻边
邻角
平行四边形中相邻的角称为 .
平行四边形的边、角有怎样的数量关系?
A
D
C
B
1、尺规作图画一个平行四边形ABCD。
2、测量 ABCD 四条边的长度和四个角的度数。
3、观察比较测量结果你有什么发现?
AB = CD AD = BC
∠A = ∠C ∠B = ∠D
A
D
C
B
发现:
求证:AB=CD,BC=DA;
∠B=∠D,∠BAD=∠DCB.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠4=∠3
AC=CA
∠2=∠1
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
已知:四边形ABCD是平行四边形。
几何语言:
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.
(平行四边形的对边相等)
∴ ∠A=∠C, ∠B=∠D
(平行四边形的对角相等)
定理1:平行四边形的两组对边分别相等
定理2:平行四边形的两组对角分别相等
例1、如图 ,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
A
C
B
D
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又∵AB+BC+CD+AD=36,
∴ AD=BC=10m
例2 :已知在 ABCD中,AB=6cm,BC=4cm,求 ABCD 的周长。
A
B
C
D
连结AC,已知 ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴C ABCD=AB+CD+BC+AD=6+6+4+4=20(cm)
例3:平行四边形ABCD中,AE⊥BC于E,CF ⊥AD于F,求证:BE=DF.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D.
又∵ AE⊥BC于E,CF ⊥AD于F,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS),
∴BE=DF.
1.在□ ABCD中,∠A:∠B=1:2,则∠A= _____ ,∠B= ______,∠C= ______, ∠D= _______.
2.已知□ ABCD的周长为30cm,且AD-AB=1cm,则 BC= ______,CD= ______ .
8cm
7cm
60°
120°
120°
60°
反馈检测
3.如图,四边形ABCD是平行四边形,则
∠A:∠B :∠C: ∠D的值可以是( )。
A: 1:2:3:4 B:1:2:2:1
C: 2:2:1:1 D: 1:2:1:2
D
A
D
C
B
4.已知, ABCD 的周长为100 cm,两邻边之差为30cm,求 ABCD较短边的长。
反馈检测
课堂小结 :
1、定义:两组对边分别平行的四边形叫做平行四边形.
2、性质:平行四边形的对边平行且相等.
平行四边形的对角相等,邻角互补.
3、数学思想:转化思想.
作 业
习题18.1:
必做题:第1题、第2题
选做题:第8题。
