10.4.1线段的垂直平分线及其作图 同步练习(含答案)
文档属性
| 名称 | 10.4.1线段的垂直平分线及其作图 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 15:24:58 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
4 线段的垂直平分线
第1课时 线段的垂直平分线及其作图
知识梳理
1.定理:线段垂直平分线上的点到这条线段__________的距离相等.
2.定理:到线段两个端点距离相等的点在这条线段的___上.
基础练习
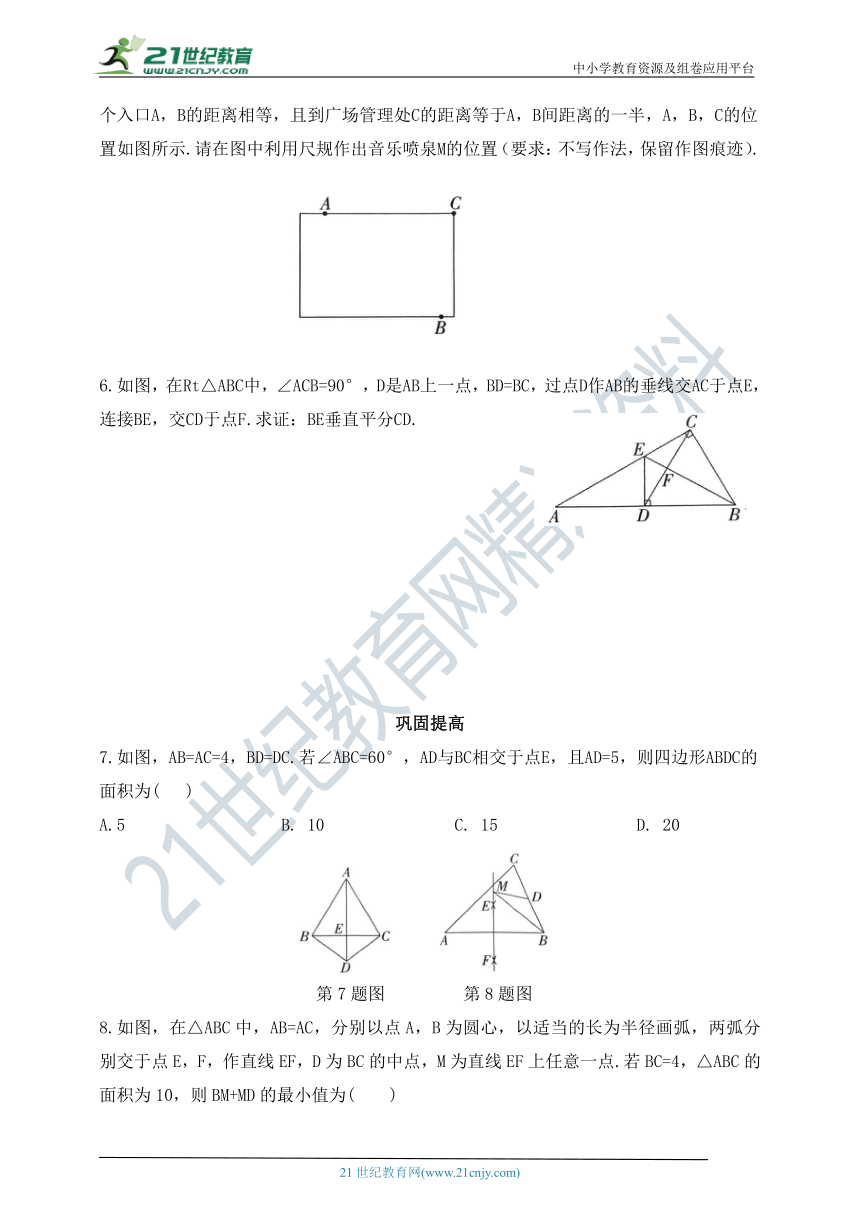
1.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为( )
A.8 B. 11 C. 16 D. 17
第1题图 第2题图
2.如图,点P在线段AB外,且PA=PB.求证:点P在线段AB的垂直平分线上.在证明该结论时,需添加辅助线,则下列作法不正确的是( )
A.作∠APB的平分线PC交AB于点C B.过点P作PC⊥AB于点C,且AC=BC
C.取AB的中点C,连接PC D.过点P作PC⊥AB,垂足为C
3.如图,在△ABC中,AB=AC,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC,AB于点D和点E.若∠B=50°,则∠CAD的度数是( )
A.30° B.40° C.50° D.60°
第3题图 第4题图
4.如图,在Rt△ABC中,∠B=90°,AB=8,BC=4,AC的垂直平分线交AB于点M,交AC于点N,则BM的长为__________.
5.某地区拟在新竣工的长方形广场的内部修建―个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A,B间距离的一半,A,B,C的位置如图所示.请在图中利用尺规作出音乐喷泉M的位置(要求:不写作法,保留作图痕迹).
6.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,连接BE,交CD于点F.求证:BE垂直平分CD.
巩固提高
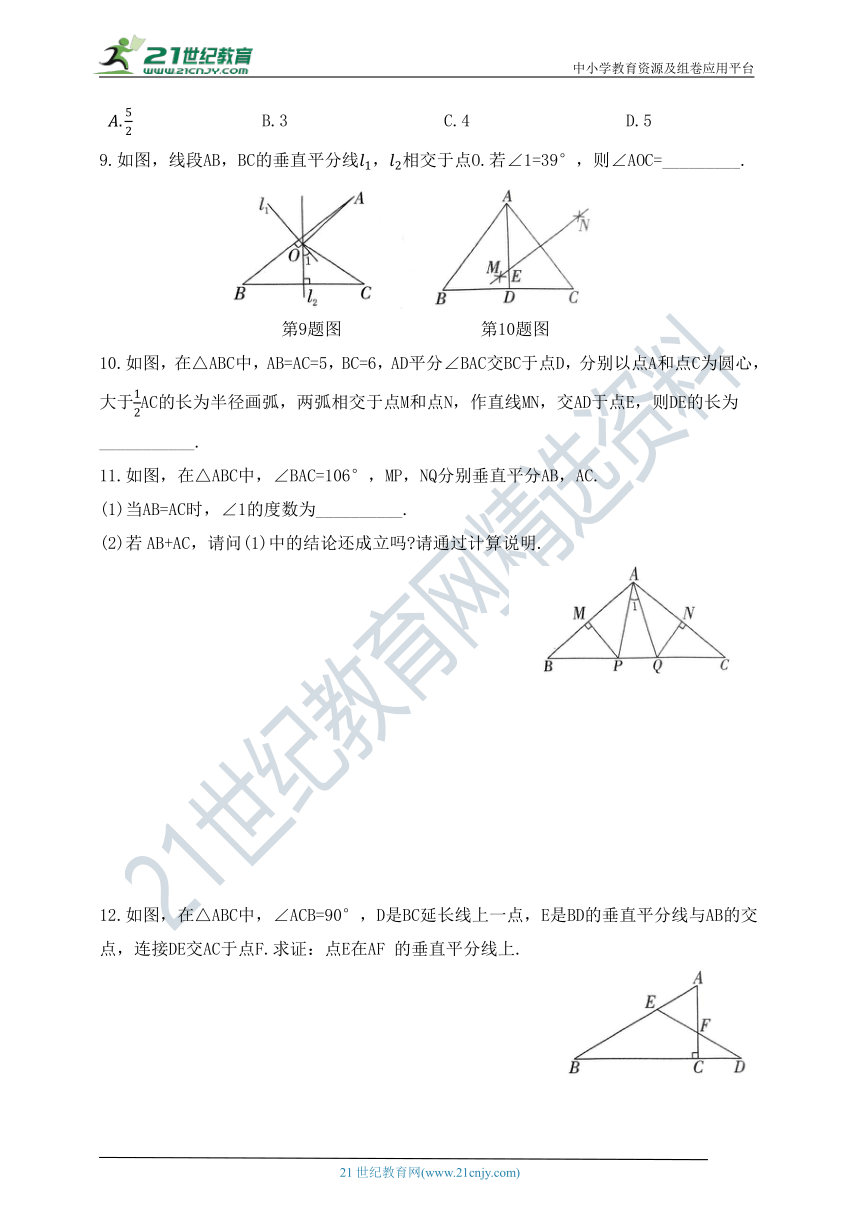
7.如图,AB=AC=4,BD=DC.若∠ABC=60°,AD与BC相交于点E,且AD=5,则四边形ABDC的面积为( )
A.5 B. 10 C. 15 D. 20
第7题图 第8题图
8.如图,在△ABC中,AB=AC,分别以点A,B为圆心,以适当的长为半径画弧,两弧分别交于点E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4,△ABC的面积为10,则BM+MD的最小值为( )
B.3 C.4 D.5
9.如图,线段AB,BC的垂直平分线,相交于点O.若∠1=39°,则∠AOC=_________.
第9题图 第10题图
10.如图,在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M和点N,作直线MN,交AD于点E,则DE的长为___________.
11.如图,在△ABC中,∠BAC=106°,MP,NQ分别垂直平分AB,AC.
(1)当AB=AC时,∠1的度数为__________.
(2)若AB+AC,请问(1)中的结论还成立吗 请通过计算说明.
12.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,连接DE交AC于点F.求证:点E在AF 的垂直平分线上.
13.如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M.求证:EM=EC.
参考答案
[知识梳理]
1.两个端点 2.垂直平分线
[基础练习]
1.B 2.B 3.A 4.3
5.音乐喷泉M的位置如图所示
6.∵∠ACB=90°,DE⊥AB,∴∠ACB=∠BDE=90°.在Rt△BDE和Rt△BCE中, ∴ Rt△BDE≌Rt△BCE.∴ED=EC.∵BD=BC,∴BE垂直平分CD .
[巩固提高]
7.B 8.D 9.78° 10.
11.(1)32°
(2)成立 ∵∠BAC=106°,∴∠B+∠C=180°-106°=74°.∵MP,NQ分别垂直平分AB,AC,∴PB=PA,QC=QA.∴∠PAB=∠B,∠QAC=∠C.∴∠PAB+∠QAC=∠B+∠C=74°.∴∠1=∠BAC-(PAB+△QAC)=106°-74°=32°.
12.∵E是BD垂直平分线上的一点,∴EB=ED.∴∠B=∠D.又∵∠ACB=90°,∴∠A=90°-∠B,∠CFD=90°-∠D.∴∠CFD=∠A.又∵∠AFE=∠CFD,∴∠AFE=∠A.∴EF=EA.∴点E在AF的垂直平分线上.
13.连接AD.∵DN是AB的垂直平分线,∴AD=BD.∴∠B=∠DAB,又∵∠B=22.5°,∴∠ADE=∠B+∠DAB=45°.∵AE⊥BC,∴∠AED=90°.∴∠DAE=45°=∠ADE.∴DE=AE.∵AE⊥BC,DF⊥AC,∴∠DEM=∠AEC=∠AFM=90°.又∵∠DME=∠AMF,∴∠MDE=∠CAE.
在△DEM和△AEC中,∴△DEM≌△AEC.∴EM=EC .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
4 线段的垂直平分线
第1课时 线段的垂直平分线及其作图
知识梳理
1.定理:线段垂直平分线上的点到这条线段__________的距离相等.
2.定理:到线段两个端点距离相等的点在这条线段的___上.
基础练习
1.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为( )
A.8 B. 11 C. 16 D. 17
第1题图 第2题图
2.如图,点P在线段AB外,且PA=PB.求证:点P在线段AB的垂直平分线上.在证明该结论时,需添加辅助线,则下列作法不正确的是( )
A.作∠APB的平分线PC交AB于点C B.过点P作PC⊥AB于点C,且AC=BC
C.取AB的中点C,连接PC D.过点P作PC⊥AB,垂足为C
3.如图,在△ABC中,AB=AC,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC,AB于点D和点E.若∠B=50°,则∠CAD的度数是( )
A.30° B.40° C.50° D.60°
第3题图 第4题图
4.如图,在Rt△ABC中,∠B=90°,AB=8,BC=4,AC的垂直平分线交AB于点M,交AC于点N,则BM的长为__________.
5.某地区拟在新竣工的长方形广场的内部修建―个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A,B间距离的一半,A,B,C的位置如图所示.请在图中利用尺规作出音乐喷泉M的位置(要求:不写作法,保留作图痕迹).
6.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,连接BE,交CD于点F.求证:BE垂直平分CD.
巩固提高
7.如图,AB=AC=4,BD=DC.若∠ABC=60°,AD与BC相交于点E,且AD=5,则四边形ABDC的面积为( )
A.5 B. 10 C. 15 D. 20
第7题图 第8题图
8.如图,在△ABC中,AB=AC,分别以点A,B为圆心,以适当的长为半径画弧,两弧分别交于点E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4,△ABC的面积为10,则BM+MD的最小值为( )
B.3 C.4 D.5
9.如图,线段AB,BC的垂直平分线,相交于点O.若∠1=39°,则∠AOC=_________.
第9题图 第10题图
10.如图,在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M和点N,作直线MN,交AD于点E,则DE的长为___________.
11.如图,在△ABC中,∠BAC=106°,MP,NQ分别垂直平分AB,AC.
(1)当AB=AC时,∠1的度数为__________.
(2)若AB+AC,请问(1)中的结论还成立吗 请通过计算说明.
12.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,连接DE交AC于点F.求证:点E在AF 的垂直平分线上.
13.如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M.求证:EM=EC.
参考答案
[知识梳理]
1.两个端点 2.垂直平分线
[基础练习]
1.B 2.B 3.A 4.3
5.音乐喷泉M的位置如图所示
6.∵∠ACB=90°,DE⊥AB,∴∠ACB=∠BDE=90°.在Rt△BDE和Rt△BCE中, ∴ Rt△BDE≌Rt△BCE.∴ED=EC.∵BD=BC,∴BE垂直平分CD .
[巩固提高]
7.B 8.D 9.78° 10.
11.(1)32°
(2)成立 ∵∠BAC=106°,∴∠B+∠C=180°-106°=74°.∵MP,NQ分别垂直平分AB,AC,∴PB=PA,QC=QA.∴∠PAB=∠B,∠QAC=∠C.∴∠PAB+∠QAC=∠B+∠C=74°.∴∠1=∠BAC-(PAB+△QAC)=106°-74°=32°.
12.∵E是BD垂直平分线上的一点,∴EB=ED.∴∠B=∠D.又∵∠ACB=90°,∴∠A=90°-∠B,∠CFD=90°-∠D.∴∠CFD=∠A.又∵∠AFE=∠CFD,∴∠AFE=∠A.∴EF=EA.∴点E在AF的垂直平分线上.
13.连接AD.∵DN是AB的垂直平分线,∴AD=BD.∴∠B=∠DAB,又∵∠B=22.5°,∴∠ADE=∠B+∠DAB=45°.∵AE⊥BC,∴∠AED=90°.∴∠DAE=45°=∠ADE.∴DE=AE.∵AE⊥BC,DF⊥AC,∴∠DEM=∠AEC=∠AFM=90°.又∵∠DME=∠AMF,∴∠MDE=∠CAE.
在△DEM和△AEC中,∴△DEM≌△AEC.∴EM=EC .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
