2021—2022学年沪科版数学九年级下册第25章投影与视图单元测试卷(Word版含答案)
文档属性
| 名称 | 2021—2022学年沪科版数学九年级下册第25章投影与视图单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 266.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 17:45:08 | ||
图片预览

文档简介
第25章 投影与视图 单元测试卷
一、单选题(共10题;每小题4分,共40分,请将答案代号填写在下面表格内)
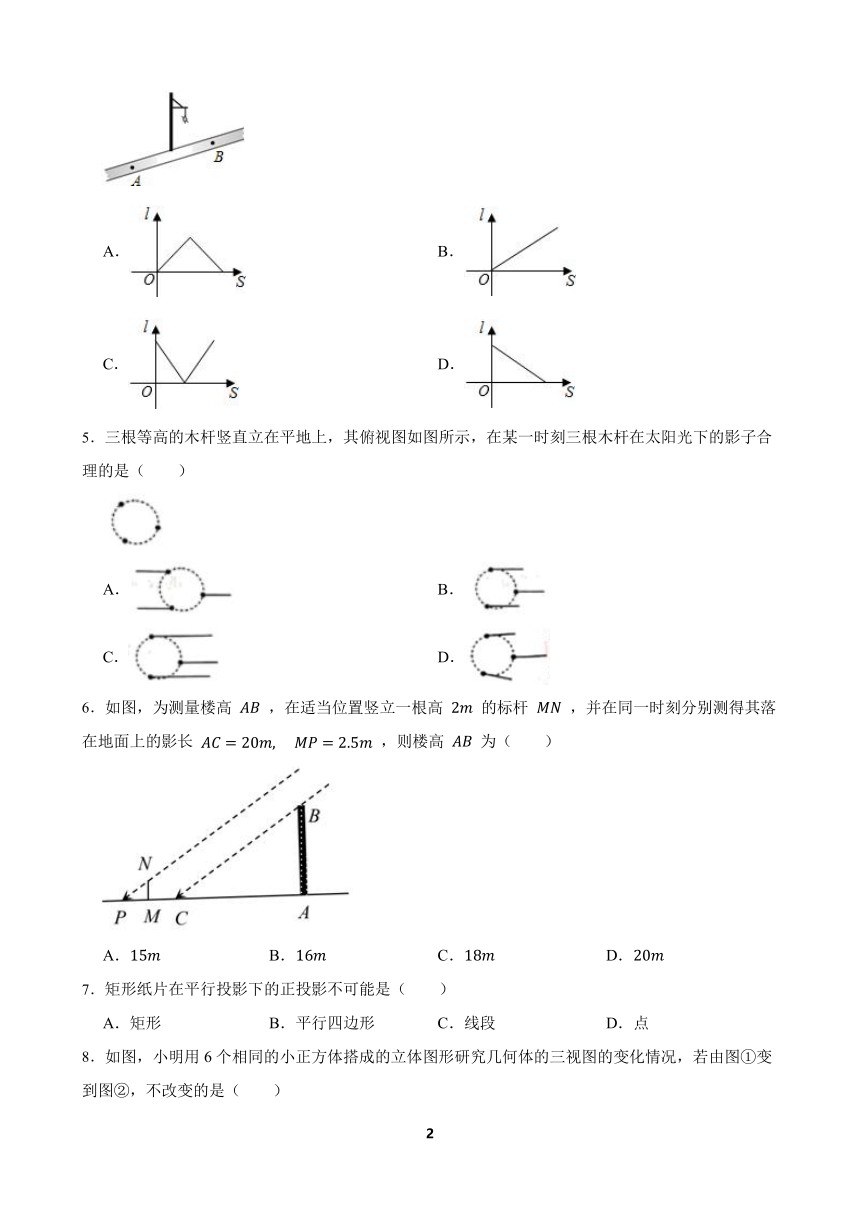
1.如图是一个由5个相同的小正方体组成的立体图形,其左视图是( )
A. B.
C. D.
2.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3 B.4 C.5 D.6
3.如图,有一路灯杆AP,路灯P距地面4.8m,身高1.6m的小明站在距A点4.8m的点D处,小明的影子为DE,他沿射线DA走2.4m到达点B处,小明的影子为BC,此时小明影子的长度( )
A.增长了1m B.缩短了1m C.增长了1.2m D.缩短了1.2m
4.如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )
A. B.
C. D.
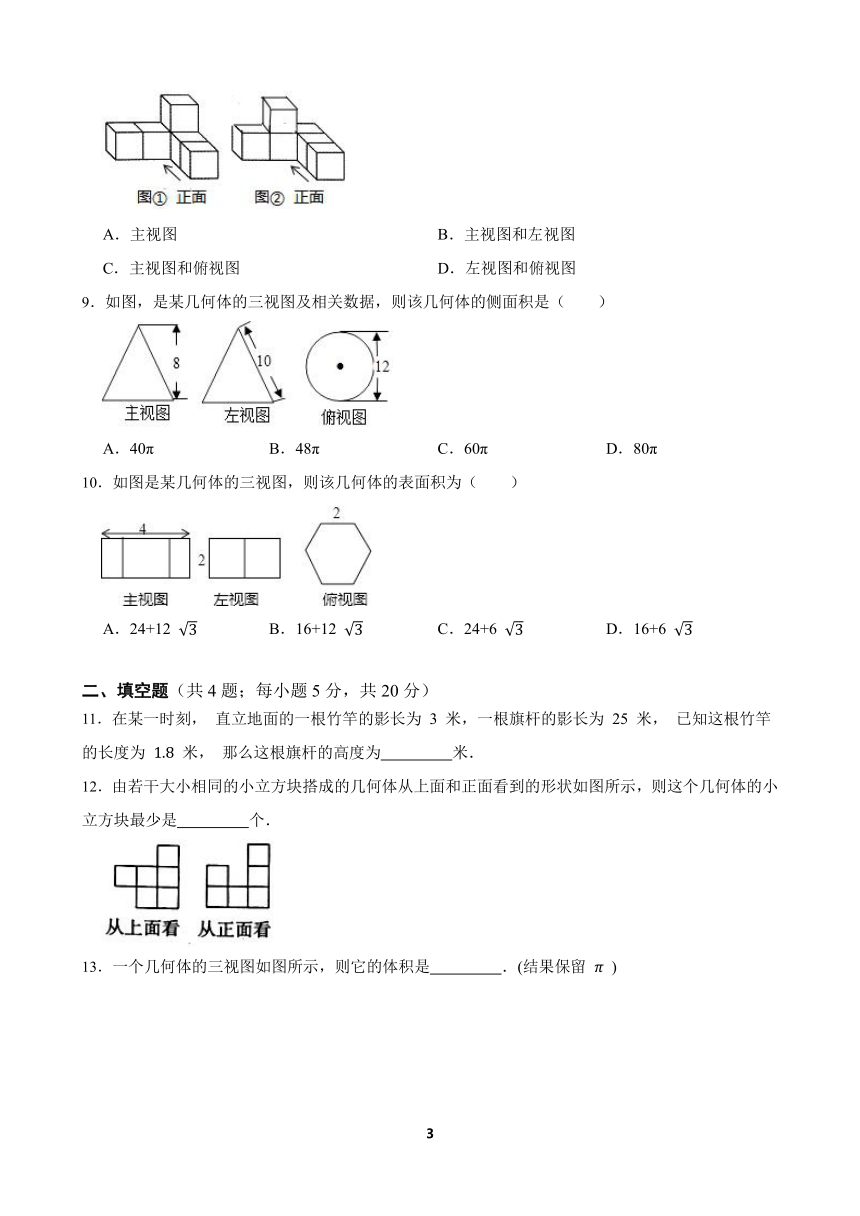
5.三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
A. B.
C. D.
6.如图,为测量楼高 ,在适当位置竖立一根高 的标杆 ,并在同一时刻分别测得其落在地面上的影长 ,则楼高 为( )
A. B. C. D.
7.矩形纸片在平行投影下的正投影不可能是( )
A.矩形 B.平行四边形 C.线段 D.点
8.如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图①变到图②,不改变的是( )
A.主视图 B.主视图和左视图
C.主视图和俯视图 D.左视图和俯视图
9.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.40π B.48π C.60π D.80π
10.如图是某几何体的三视图,则该几何体的表面积为( )
A.24+12 B.16+12 C.24+6 D.16+6
二、填空题(共4题;每小题5分,共20分)
11.在某一时刻, 直立地面的一根竹竿的影长为 3 米,一根旗杆的影长为 25 米, 已知这根竹竿的长度为 米, 那么这根旗杆的高度为 米.
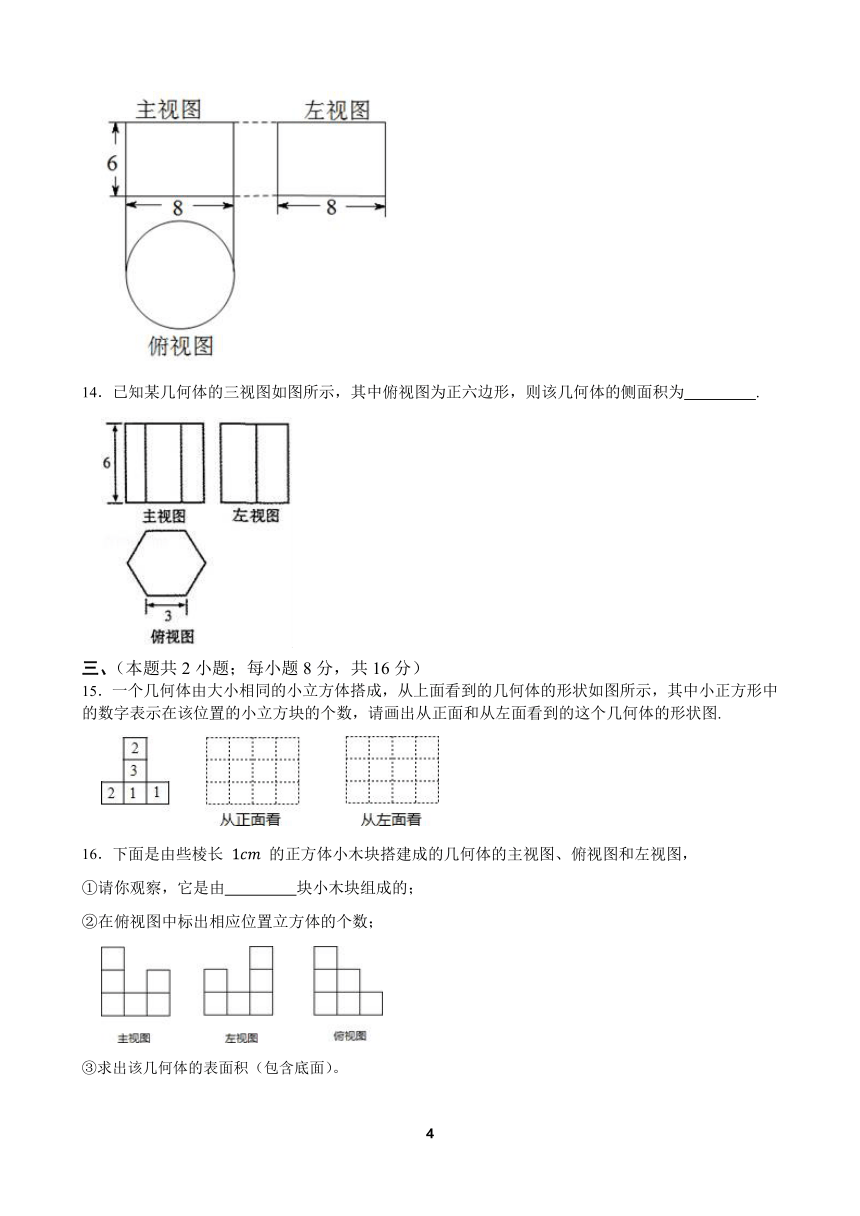
12.由若干大小相同的小立方块搭成的几何体从上面和正面看到的形状如图所示,则这个几何体的小立方块最少是 个.
13.一个几何体的三视图如图所示,则它的体积是 .(结果保留 )
14.已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为 .
三、(本题共2小题;每小题8分,共16分)
15.一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
16.下面是由些棱长 的正方体小木块搭建成的几何体的主视图、俯视图和左视图,
①请你观察,它是由 块小木块组成的;
②在俯视图中标出相应位置立方体的个数;
③求出该几何体的表面积(包含底面)。
四、(本题共2小题;每小题8分,共16分)
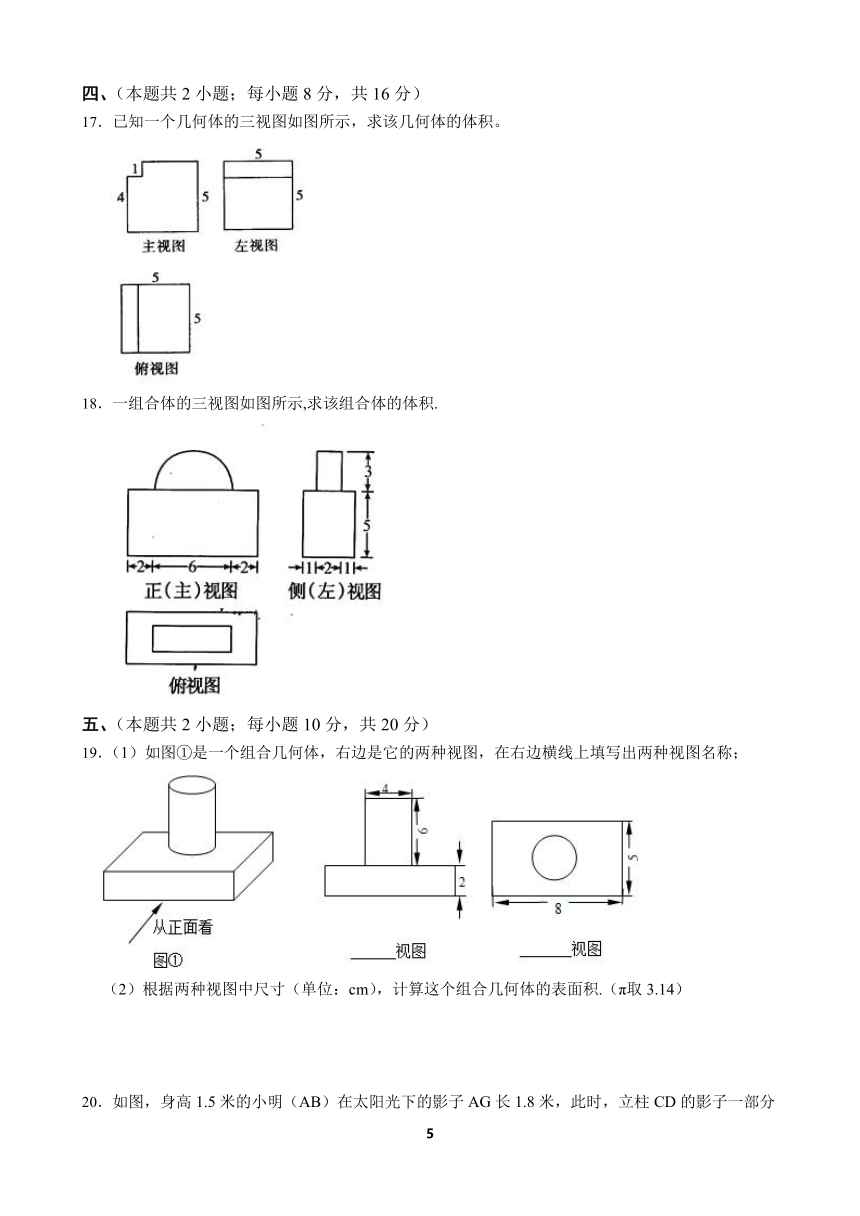
17.已知一个几何体的三视图如图所示,求该几何体的体积。
18.一组合体的三视图如图所示,求该组合体的体积.
五、(本题共2小题;每小题10分,共20分)
19.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
20.如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分落在地面CE上,一部分落在墙EF上.
(1)请你在墙上画出表示CD的部分影子EH;
(2)若量得CE=1.2米,EH=1.5米,求立柱CD的高.
六、(本题12分)
21.用棱长为 的若干小正方体按如所示的规律在地面上搭建若干个几何体.图中每个几何体自上而下分别叫第一层、第二层, ,第 层( 为正整数)
(1)搭建第④个几何体的小立方体的个数为 .
(2)分别求出第②、③个几何体的所有露出部分(不含底面)的面积。
(3)为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂 需要油漆0.2克,求喷涂第20个几何体,共需要多少克油漆?
七、(本题12分)
22.如图,A、B、C分别表示甲、乙、丙三个物体的顶端,甲物体高3米,影长2米,乙物体高2米,影长3米,甲乙两物体相距4米.
(1)请在图中画出光源灯的位置及灯杆,并画出物体丙的影子.
(2)若甲、乙、丙及灯杆都与地面垂直,且在同一直线上,求灯杆的高度.
八、(本题14分)
23.如图所示,一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,液面刚好过棱CD,并与棱BB'交于点Q.此时液体的形状为直三棱柱,其三视图及尺寸见下图所示请解决下列问题:
(1)CQ与BE的位置关系是 ,BQ的长是 dm:
(2)求液体的体积;(提示:直棱柱体积=底面积×高);
(3)若容器底部的倾斜角∠CBE=α,求α的度数。(参考:sin49°=cos41°= ,tan37°= )
第25章 投影与视图 单元测试卷(沪科版九年级下)
答案解析
一、单选题:(共10题;每小题4分,共40分) DDDCB BDDCA
1.【答案】D
【解析】【从左边看图形,左边是两个小正方形,右边是一个小正方形,
2.【答案】D
【解析】【解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,
∵P(2,2),A(0,1),B(3,1).∴PD=1,PE=2,AB=3,
∵AB//A′B′,∴△PAB∽△PA′B′,∴,即,∴A′B′=6,
【分析】根据平行线可证△PAB∽△PA′B′,利用相似三角形的性质求解即可.
3.【答案】D
【解析】【解:过B作BG⊥AE交PC于G,过D作DH⊥AE交PE于H,
则AB=AD-BD=4.8-2.4=2.4(m),BG=DH=1.6m,BG∥AP∥DH,
∴△BCG∽△ACP,△DEH∽△AEP,∴,
即,解得:BC=1.2,DE=2.4,
∴DE-BC=2.4-1.2=1.2(m),即此时小明影子的长度缩短了1.2m.
【分析】先求出△BCG∽△ACP,△DEH∽△AEP,再求出BC=1.2,DE=2.4,最后求解即可。
4.【答案】C
【解析】【∵小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程S之间的变化关系应为:当小红走到灯下以前:l随S的增大而减小;当小红走到灯下以后再往前走时:l随S的增大而增大,∴用图象刻画出来应为C.故答案为:C.
【分析】根据中心投影的性质得出小红在路灯下走的过程中影长随路程之间的变化:先变短后变长,在路灯下时影子为一个点,进而得出结论。
5.【答案】B
【解析】【解:A.在某一时刻三根木杆在太阳光下的影子的方向应该一致,故本选项不符合题意;
B.在某一时刻三根木杆在太阳光下的影子合理,故本选项符合题意;
C.在某一时刻三根等高木杆在太阳光下的影子的长度应该相同,故本选项不符合题意;
D.在某一时刻三根木杆在太阳光下的影子的方向应该互相平行,故本选项不符合题意.
【分析】 三根等高的木杆竖直立在平地上 , 在某一时刻三根木杆在太阳光下的影子 应该同方向、长度相等且平行,据此判断即可.
6.【答案】B
【解析】【解:∵ , ∴ ,∴AB=16(米).故答案为:B.
【分析】利用同一时刻,同一地点,同一平面上,不同物体的高度与影长成比例建立方程,可求出AB的长.
7.【答案】D
【解析】【解:阳光射在地面上,当矩形纸片与太阳光垂直时,矩形纸片在地面上的影子为矩形;当矩形纸片与太阳光斜交时,矩形纸片在地面上的影子为平行四边形;当矩形纸片与太阳光平行时,矩形纸片在地面上的影子为线段.故答案为:D.
【分析】在太阳光下的投影为平行投影,平行投影不可能把矩形投影为一个点.
8.【答案】D
【解析】【解:从左面看第一层都是三个小正方形,第二层左边一个小正方形,①②的左视图
相同;
从上面看第一列都是一个小正方形,第二列都是一个小正方形,第三列都是三个小正方形,
故①②的俯视图相同,故答案为:D.
【分析】从一个几何体的正面、左面、上面看得到的正投影就分别是该几何体的主视图、左视图及俯视图,根据定义即可一一判断得出答案.
9.【答案】C
【解析】【解:由三视图知:几何体是圆锥,
∵底面直径为12,高为8,圆锥的母线长为10,
∴圆锥的侧面积S=π×6×10=60π.故答案为:C.
【分析】从三个视图观察,此几何体是圆锥,圆锥的侧面展开图是扇形,从图中的数据可知圆锥的母线长(R)、底面圆的直径(半径为r)、圆锥的高。根据公式:圆锥的侧面积S=πRr,即可求解。
10.【答案】A
【解析】【解:观察该几何体的三视图发现该几何体为正六棱柱;
该六棱柱的棱长为2,正六边形的半径为2,
所以表面积为2×2×6+ ×2× ×6×2=24+12 ,故答案为:A.
【分析】观察几何体的三视图,先确定该几何体的形状,再根据各部分的尺寸求出该几何体的表面积。
11.【答案】15
【解析】【解:设这根旗杆的高度为h米,根据题意得:
,解得: 即这根旗杆的高度为15米.故答案为:15
【分析】先求出,再计算求解即可。
12.【答案】9
【解析】【解:如图,这个几何体的小立方体的个数最少(个,
故答案为:9.
13.【答案】
【解析】解:由三视图可得,该几何体是一个底面直径为8,高为6的圆柱体,
∴该几何体的体积为:
14.【答案】108
【解析】【:观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为3,高为6,
所以其侧面积为3×6×6=108,故答案为:108.
15.【答案】解:由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,1;左视图有3列,每列小正方形数目分别为2,3,2.据此可画出图形.
如图所示:
【解析】主视图就是从正面看得到的图形,主视图有3列,从左至右每列小正方数形数目分别为2,3,1;左视图就是从左面看得到的图形,左视图有3列,从左至右每列小正方形数目分别为2,3,2,据此可画出图形.
16.【答案】解:①∵俯视图中有 个正方形,
∴最底层有 个正方体小木块,
由主视图和左视图可得第二层有 个正方体小木块,第三层有 个正方体小木块,
∴共有 个正方体小木块组成.
②根据①得:
③表面积为:
【解析】(1)由俯视图可以看出底层有6个小正方体, 由主视图和左视图可得第二层有 个正方体小木块,第三层有 个正方体小木块, 从而得出搭出该几何体的小正方体的个数;
(2)根据三个视图及(1)得出的搭该几何体的小正方体的总个数,剪开得出答案;
(3)该几何体的表面积应该等于其主视图,俯视图,左视图的面积和的2,再加上第一列中间低处的那个露出的连个面,第一行中间低处的那一个露出的两个面即可。
17.【答案】解:由三视图可其看成为两个长方体上、下叠放而成。
下面的长方体的长、宽、高分别为5、5、4;
上面的长方体的长、宽、高分别为5、4、1;
则该组合体的体积是5×5×4+5×4×1=120.
【解析】由三视图将该几何看成是由两个长方体靠右对齐叠放而成;由标出的数据确定每个长方体的长宽高,从而计算两个长方体的体积和。
18.【答案】解:该组合体是由半圆柱体和长方体上、下叠放而后的。
半圆柱体的上下底面半径为,高为2,
长方体的长、宽、高分别为(2+6+2)、(1+2+1)、5,即为10、4、5
则该组合体的体积为
【解析】由主视图可知该组合体分为上、下两个几何体,上面的几何体为半圆柱体,通过主视图和左视图可得底面半径为3,高为2;下面的几何体是长方体,不难得出其长、宽、高,计算它们的体积和即可。
19.【答案】(1)主,俯
(2)组合几何体的表面积=2×(8×5+8×2+5×2)+4×π×6=2×66+24×3.14=207. 36(cm2).
【解析】(1)解:如图所示:
;
故答案为:主,俯;
(1)主视图就是从正面看得到的图形,俯视图就是从上面看得到的图形,左视图就是从左面看得到的图形,注意所有能看见的轮廓线都必须表现在视图中,据此即可判断得出答案;
(2)根据表面积=长方体的表面积+圆柱的侧面积进行计算.
20.【答案】(1)解:如图,线段EH为所求;
(2)解:过点E作EM//BG,交CD于点M,
则四边形DHEM是平行四边形,△ABG∽△CME,
即DM=EH=1.5,
∵ ,∴ ∴
∴ (米), 故立柱CD的高为2.5米.
【解析】(1)根据题意作图求解即可;
(2)先求出 DM=EH=1.5, 再求出CM=1,最后计算求解即可。
21.【答案】(1)30
(2)解:第②个几何体的三视图如下:
由题意,每个小正方形的面积为 ,
则第②个几何体的所有露出部分(不含底面)面积为 ;
第③个几何体的三视图如下:
则第③个几何体的所有露出部分(不含底面)面积为
(3)解:第20个几何体从第1层到第20层小立方体的个数依次为 ,
则第20个几何体的所有露出部分(不含底面)面积为 ,
因此,共需要油漆的克数为 (克),答:共需要992克油漆
【解析】(1)搭建第①个几何体的小立方体的个数为1,
搭建第②个几何体的小立方体的个数为 ,
搭建第③个几何体的小立方体的个数为 ,
归纳类推得:搭建第④个几何体的小立方体的个数为 ,
故答案为:30;
(1)归纳出前3个几何体的规律即可得;(2)分别画出两个几何体的三视图,再根据四个侧面和向上的面的小正方形的个数即可得;(3)先根据(1)的方法得出第20个几何体每一层小立方体的个数,再根据(2)的方法得出第20个几何体的所有露出部分(不含底面)的面积,然后乘以 即可得.
22.【答案】(1)点O为灯的位置,QF为丙物体的影子;
(2)作OM⊥QH,设OM=x,EM=y,
由△GAE∽△GOM得 ,即: ①,
由△BDH∽△OMH得 即: ②
结合①②得,x=6,y=2. 经检验,x=6、y=2是方程的解,
答:灯的高度为6米.
【解析】(1)首先由 AE:EG = 3:2及 BD:DH = 2:3确定出影子末端G、H的位置,再连接GA、HB并延长交于点O,从而确定点光源O的位置,最后连接OC并延长即可确定影子;
(2)作OM⊥QH ,设OM=x,EM=y,根据三角形相似列出比例式即可确定灯的高度.
23.【答案】(1)平行;3
(2)解:V液= ×3×4×4=24(dm3).
(3)解:∵CQ∥BE,
∴∠CBE=∠BCQ,
∵在Rt△BCQ中,tan∠BCQ= = ,
∴∠BCQ=37°,
∴α=∠BCQ=37°.
【解析】(1)CQ∥BE,BQ= =3dm.
(1)如图可直接得到CQ与BE的位置关系,再由勾股定理求BQ的长;(2)根据三视图得到直三棱柱的边长,再由直棱柱体积=底面积×高,即可求得;(3)根据两直线平行内错角相等和三角函数值,即可求得 .2
一、单选题(共10题;每小题4分,共40分,请将答案代号填写在下面表格内)
1.如图是一个由5个相同的小正方体组成的立体图形,其左视图是( )
A. B.
C. D.
2.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3 B.4 C.5 D.6
3.如图,有一路灯杆AP,路灯P距地面4.8m,身高1.6m的小明站在距A点4.8m的点D处,小明的影子为DE,他沿射线DA走2.4m到达点B处,小明的影子为BC,此时小明影子的长度( )
A.增长了1m B.缩短了1m C.增长了1.2m D.缩短了1.2m
4.如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )
A. B.
C. D.
5.三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
A. B.
C. D.
6.如图,为测量楼高 ,在适当位置竖立一根高 的标杆 ,并在同一时刻分别测得其落在地面上的影长 ,则楼高 为( )
A. B. C. D.
7.矩形纸片在平行投影下的正投影不可能是( )
A.矩形 B.平行四边形 C.线段 D.点
8.如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图①变到图②,不改变的是( )
A.主视图 B.主视图和左视图
C.主视图和俯视图 D.左视图和俯视图
9.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.40π B.48π C.60π D.80π
10.如图是某几何体的三视图,则该几何体的表面积为( )
A.24+12 B.16+12 C.24+6 D.16+6
二、填空题(共4题;每小题5分,共20分)
11.在某一时刻, 直立地面的一根竹竿的影长为 3 米,一根旗杆的影长为 25 米, 已知这根竹竿的长度为 米, 那么这根旗杆的高度为 米.
12.由若干大小相同的小立方块搭成的几何体从上面和正面看到的形状如图所示,则这个几何体的小立方块最少是 个.
13.一个几何体的三视图如图所示,则它的体积是 .(结果保留 )
14.已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为 .
三、(本题共2小题;每小题8分,共16分)
15.一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
16.下面是由些棱长 的正方体小木块搭建成的几何体的主视图、俯视图和左视图,
①请你观察,它是由 块小木块组成的;
②在俯视图中标出相应位置立方体的个数;
③求出该几何体的表面积(包含底面)。
四、(本题共2小题;每小题8分,共16分)
17.已知一个几何体的三视图如图所示,求该几何体的体积。
18.一组合体的三视图如图所示,求该组合体的体积.
五、(本题共2小题;每小题10分,共20分)
19.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
20.如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分落在地面CE上,一部分落在墙EF上.
(1)请你在墙上画出表示CD的部分影子EH;
(2)若量得CE=1.2米,EH=1.5米,求立柱CD的高.
六、(本题12分)
21.用棱长为 的若干小正方体按如所示的规律在地面上搭建若干个几何体.图中每个几何体自上而下分别叫第一层、第二层, ,第 层( 为正整数)
(1)搭建第④个几何体的小立方体的个数为 .
(2)分别求出第②、③个几何体的所有露出部分(不含底面)的面积。
(3)为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂 需要油漆0.2克,求喷涂第20个几何体,共需要多少克油漆?
七、(本题12分)
22.如图,A、B、C分别表示甲、乙、丙三个物体的顶端,甲物体高3米,影长2米,乙物体高2米,影长3米,甲乙两物体相距4米.
(1)请在图中画出光源灯的位置及灯杆,并画出物体丙的影子.
(2)若甲、乙、丙及灯杆都与地面垂直,且在同一直线上,求灯杆的高度.
八、(本题14分)
23.如图所示,一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,液面刚好过棱CD,并与棱BB'交于点Q.此时液体的形状为直三棱柱,其三视图及尺寸见下图所示请解决下列问题:
(1)CQ与BE的位置关系是 ,BQ的长是 dm:
(2)求液体的体积;(提示:直棱柱体积=底面积×高);
(3)若容器底部的倾斜角∠CBE=α,求α的度数。(参考:sin49°=cos41°= ,tan37°= )
第25章 投影与视图 单元测试卷(沪科版九年级下)
答案解析
一、单选题:(共10题;每小题4分,共40分) DDDCB BDDCA
1.【答案】D
【解析】【从左边看图形,左边是两个小正方形,右边是一个小正方形,
2.【答案】D
【解析】【解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,
∵P(2,2),A(0,1),B(3,1).∴PD=1,PE=2,AB=3,
∵AB//A′B′,∴△PAB∽△PA′B′,∴,即,∴A′B′=6,
【分析】根据平行线可证△PAB∽△PA′B′,利用相似三角形的性质求解即可.
3.【答案】D
【解析】【解:过B作BG⊥AE交PC于G,过D作DH⊥AE交PE于H,
则AB=AD-BD=4.8-2.4=2.4(m),BG=DH=1.6m,BG∥AP∥DH,
∴△BCG∽△ACP,△DEH∽△AEP,∴,
即,解得:BC=1.2,DE=2.4,
∴DE-BC=2.4-1.2=1.2(m),即此时小明影子的长度缩短了1.2m.
【分析】先求出△BCG∽△ACP,△DEH∽△AEP,再求出BC=1.2,DE=2.4,最后求解即可。
4.【答案】C
【解析】【∵小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程S之间的变化关系应为:当小红走到灯下以前:l随S的增大而减小;当小红走到灯下以后再往前走时:l随S的增大而增大,∴用图象刻画出来应为C.故答案为:C.
【分析】根据中心投影的性质得出小红在路灯下走的过程中影长随路程之间的变化:先变短后变长,在路灯下时影子为一个点,进而得出结论。
5.【答案】B
【解析】【解:A.在某一时刻三根木杆在太阳光下的影子的方向应该一致,故本选项不符合题意;
B.在某一时刻三根木杆在太阳光下的影子合理,故本选项符合题意;
C.在某一时刻三根等高木杆在太阳光下的影子的长度应该相同,故本选项不符合题意;
D.在某一时刻三根木杆在太阳光下的影子的方向应该互相平行,故本选项不符合题意.
【分析】 三根等高的木杆竖直立在平地上 , 在某一时刻三根木杆在太阳光下的影子 应该同方向、长度相等且平行,据此判断即可.
6.【答案】B
【解析】【解:∵ , ∴ ,∴AB=16(米).故答案为:B.
【分析】利用同一时刻,同一地点,同一平面上,不同物体的高度与影长成比例建立方程,可求出AB的长.
7.【答案】D
【解析】【解:阳光射在地面上,当矩形纸片与太阳光垂直时,矩形纸片在地面上的影子为矩形;当矩形纸片与太阳光斜交时,矩形纸片在地面上的影子为平行四边形;当矩形纸片与太阳光平行时,矩形纸片在地面上的影子为线段.故答案为:D.
【分析】在太阳光下的投影为平行投影,平行投影不可能把矩形投影为一个点.
8.【答案】D
【解析】【解:从左面看第一层都是三个小正方形,第二层左边一个小正方形,①②的左视图
相同;
从上面看第一列都是一个小正方形,第二列都是一个小正方形,第三列都是三个小正方形,
故①②的俯视图相同,故答案为:D.
【分析】从一个几何体的正面、左面、上面看得到的正投影就分别是该几何体的主视图、左视图及俯视图,根据定义即可一一判断得出答案.
9.【答案】C
【解析】【解:由三视图知:几何体是圆锥,
∵底面直径为12,高为8,圆锥的母线长为10,
∴圆锥的侧面积S=π×6×10=60π.故答案为:C.
【分析】从三个视图观察,此几何体是圆锥,圆锥的侧面展开图是扇形,从图中的数据可知圆锥的母线长(R)、底面圆的直径(半径为r)、圆锥的高。根据公式:圆锥的侧面积S=πRr,即可求解。
10.【答案】A
【解析】【解:观察该几何体的三视图发现该几何体为正六棱柱;
该六棱柱的棱长为2,正六边形的半径为2,
所以表面积为2×2×6+ ×2× ×6×2=24+12 ,故答案为:A.
【分析】观察几何体的三视图,先确定该几何体的形状,再根据各部分的尺寸求出该几何体的表面积。
11.【答案】15
【解析】【解:设这根旗杆的高度为h米,根据题意得:
,解得: 即这根旗杆的高度为15米.故答案为:15
【分析】先求出,再计算求解即可。
12.【答案】9
【解析】【解:如图,这个几何体的小立方体的个数最少(个,
故答案为:9.
13.【答案】
【解析】解:由三视图可得,该几何体是一个底面直径为8,高为6的圆柱体,
∴该几何体的体积为:
14.【答案】108
【解析】【:观察该几何体的三视图发现该几何体为正六棱柱,其底面边长为3,高为6,
所以其侧面积为3×6×6=108,故答案为:108.
15.【答案】解:由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,1;左视图有3列,每列小正方形数目分别为2,3,2.据此可画出图形.
如图所示:
【解析】主视图就是从正面看得到的图形,主视图有3列,从左至右每列小正方数形数目分别为2,3,1;左视图就是从左面看得到的图形,左视图有3列,从左至右每列小正方形数目分别为2,3,2,据此可画出图形.
16.【答案】解:①∵俯视图中有 个正方形,
∴最底层有 个正方体小木块,
由主视图和左视图可得第二层有 个正方体小木块,第三层有 个正方体小木块,
∴共有 个正方体小木块组成.
②根据①得:
③表面积为:
【解析】(1)由俯视图可以看出底层有6个小正方体, 由主视图和左视图可得第二层有 个正方体小木块,第三层有 个正方体小木块, 从而得出搭出该几何体的小正方体的个数;
(2)根据三个视图及(1)得出的搭该几何体的小正方体的总个数,剪开得出答案;
(3)该几何体的表面积应该等于其主视图,俯视图,左视图的面积和的2,再加上第一列中间低处的那个露出的连个面,第一行中间低处的那一个露出的两个面即可。
17.【答案】解:由三视图可其看成为两个长方体上、下叠放而成。
下面的长方体的长、宽、高分别为5、5、4;
上面的长方体的长、宽、高分别为5、4、1;
则该组合体的体积是5×5×4+5×4×1=120.
【解析】由三视图将该几何看成是由两个长方体靠右对齐叠放而成;由标出的数据确定每个长方体的长宽高,从而计算两个长方体的体积和。
18.【答案】解:该组合体是由半圆柱体和长方体上、下叠放而后的。
半圆柱体的上下底面半径为,高为2,
长方体的长、宽、高分别为(2+6+2)、(1+2+1)、5,即为10、4、5
则该组合体的体积为
【解析】由主视图可知该组合体分为上、下两个几何体,上面的几何体为半圆柱体,通过主视图和左视图可得底面半径为3,高为2;下面的几何体是长方体,不难得出其长、宽、高,计算它们的体积和即可。
19.【答案】(1)主,俯
(2)组合几何体的表面积=2×(8×5+8×2+5×2)+4×π×6=2×66+24×3.14=207. 36(cm2).
【解析】(1)解:如图所示:
;
故答案为:主,俯;
(1)主视图就是从正面看得到的图形,俯视图就是从上面看得到的图形,左视图就是从左面看得到的图形,注意所有能看见的轮廓线都必须表现在视图中,据此即可判断得出答案;
(2)根据表面积=长方体的表面积+圆柱的侧面积进行计算.
20.【答案】(1)解:如图,线段EH为所求;
(2)解:过点E作EM//BG,交CD于点M,
则四边形DHEM是平行四边形,△ABG∽△CME,
即DM=EH=1.5,
∵ ,∴ ∴
∴ (米), 故立柱CD的高为2.5米.
【解析】(1)根据题意作图求解即可;
(2)先求出 DM=EH=1.5, 再求出CM=1,最后计算求解即可。
21.【答案】(1)30
(2)解:第②个几何体的三视图如下:
由题意,每个小正方形的面积为 ,
则第②个几何体的所有露出部分(不含底面)面积为 ;
第③个几何体的三视图如下:
则第③个几何体的所有露出部分(不含底面)面积为
(3)解:第20个几何体从第1层到第20层小立方体的个数依次为 ,
则第20个几何体的所有露出部分(不含底面)面积为 ,
因此,共需要油漆的克数为 (克),答:共需要992克油漆
【解析】(1)搭建第①个几何体的小立方体的个数为1,
搭建第②个几何体的小立方体的个数为 ,
搭建第③个几何体的小立方体的个数为 ,
归纳类推得:搭建第④个几何体的小立方体的个数为 ,
故答案为:30;
(1)归纳出前3个几何体的规律即可得;(2)分别画出两个几何体的三视图,再根据四个侧面和向上的面的小正方形的个数即可得;(3)先根据(1)的方法得出第20个几何体每一层小立方体的个数,再根据(2)的方法得出第20个几何体的所有露出部分(不含底面)的面积,然后乘以 即可得.
22.【答案】(1)点O为灯的位置,QF为丙物体的影子;
(2)作OM⊥QH,设OM=x,EM=y,
由△GAE∽△GOM得 ,即: ①,
由△BDH∽△OMH得 即: ②
结合①②得,x=6,y=2. 经检验,x=6、y=2是方程的解,
答:灯的高度为6米.
【解析】(1)首先由 AE:EG = 3:2及 BD:DH = 2:3确定出影子末端G、H的位置,再连接GA、HB并延长交于点O,从而确定点光源O的位置,最后连接OC并延长即可确定影子;
(2)作OM⊥QH ,设OM=x,EM=y,根据三角形相似列出比例式即可确定灯的高度.
23.【答案】(1)平行;3
(2)解:V液= ×3×4×4=24(dm3).
(3)解:∵CQ∥BE,
∴∠CBE=∠BCQ,
∵在Rt△BCQ中,tan∠BCQ= = ,
∴∠BCQ=37°,
∴α=∠BCQ=37°.
【解析】(1)CQ∥BE,BQ= =3dm.
(1)如图可直接得到CQ与BE的位置关系,再由勾股定理求BQ的长;(2)根据三视图得到直三棱柱的边长,再由直棱柱体积=底面积×高,即可求得;(3)根据两直线平行内错角相等和三角函数值,即可求得 .2
