2021—2022学年人教版八年级数学下册18.2.3正方形课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.2.3正方形课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 140.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 00:00:00 | ||
图片预览


文档简介
第十八章 平行四边形18.2.3正方形 课后练习
一、选择题
1.下列说法错误的是( )
A.平行四边形对边平行且相等 B.菱形的对角线平分一组对角
C.矩形的对角线互相垂直 D.正方形有四条对称轴
2.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90° B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD D.当 ABCD是菱形时,AB=AC
3.如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,则∠EAF=( )度
A.30° B.45° C.50° D.60°
4.如图,正方形ABCD的边长是4,点E是DC上一个点,且DE=1,P点在AC上移动,则PE+PD的最小值是( )
A.4 B.4.5 C.5.5 D.5
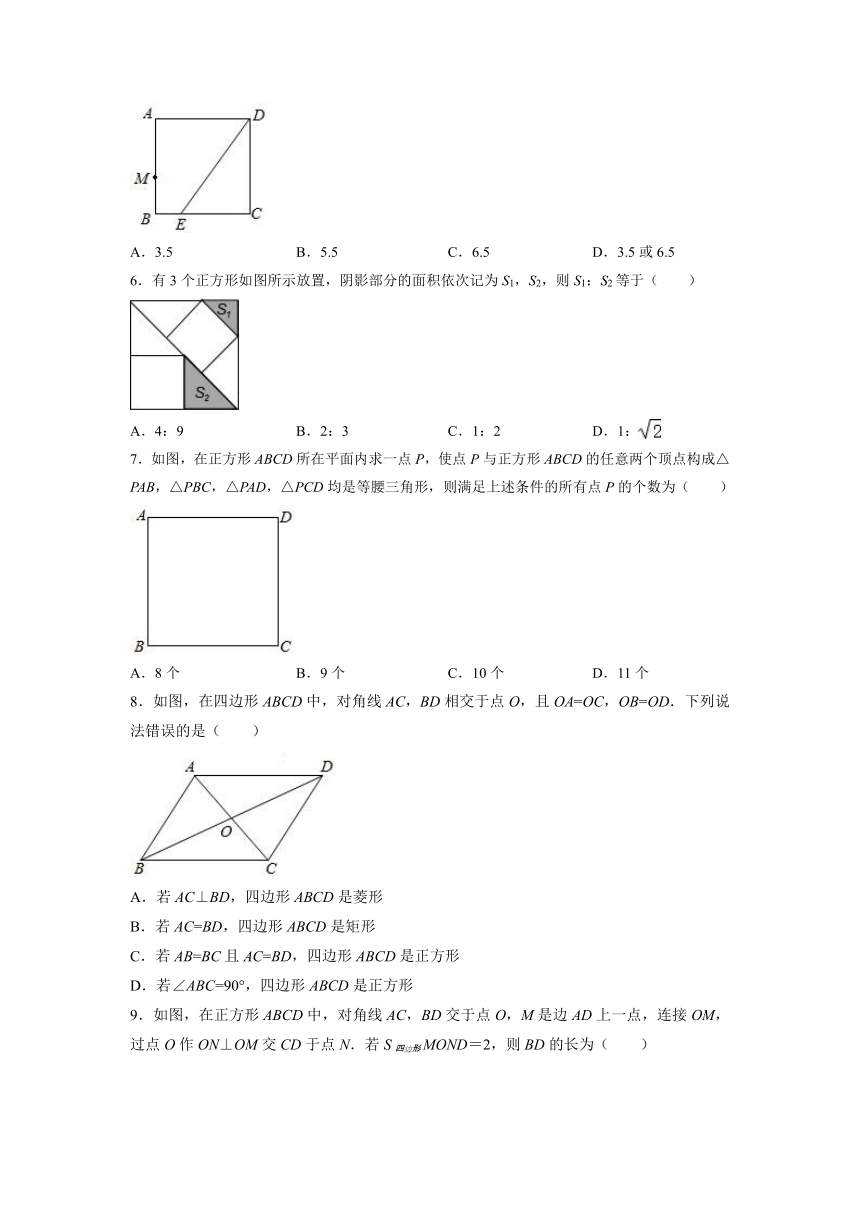
5.如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
6.有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )
A.4:9 B.2:3 C.1:2 D.1:
7.如图,在正方形ABCD所在平面内求一点P,使点P与正方形ABCD的任意两个顶点构成△PAB,△PBC,△PAD,△PCD均是等腰三角形,则满足上述条件的所有点P的个数为( )
A.8个 B.9个 C.10个 D.11个
8.如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.下列说法错误的是( )
A.若AC⊥BD,四边形ABCD是菱形
B.若AC=BD,四边形ABCD是矩形
C.若AB=BC且AC=BD,四边形ABCD是正方形
D.若∠ABC=90°,四边形ABCD是正方形
9.如图,在正方形ABCD中,对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM交CD于点N.若S四边形MOND=2,则BD的长为( )
A.2 B. C.4 D.2
10.如图,在等腰直角中,,以B为圆心,小于的长为半径画弧,分别交,于点E,F,分别以点E,F为圆心,大于的长为半径画弧,两弧交于点P,作射线交于点O,在射线上作,连接,.下列说法不正确的是( )
A. B. C. D.若四边形的周长为16,则
二、填空题
11.如图,P是正方形ABCD内一点,且PA=PD,PB=PC.若∠PBC=60°,则∠PAD=_____.
12.如图,正方形ABCD边长为2,点P在BC边上,DP交AC于点E,∠ADE=∠AED,则BP的长度是 .
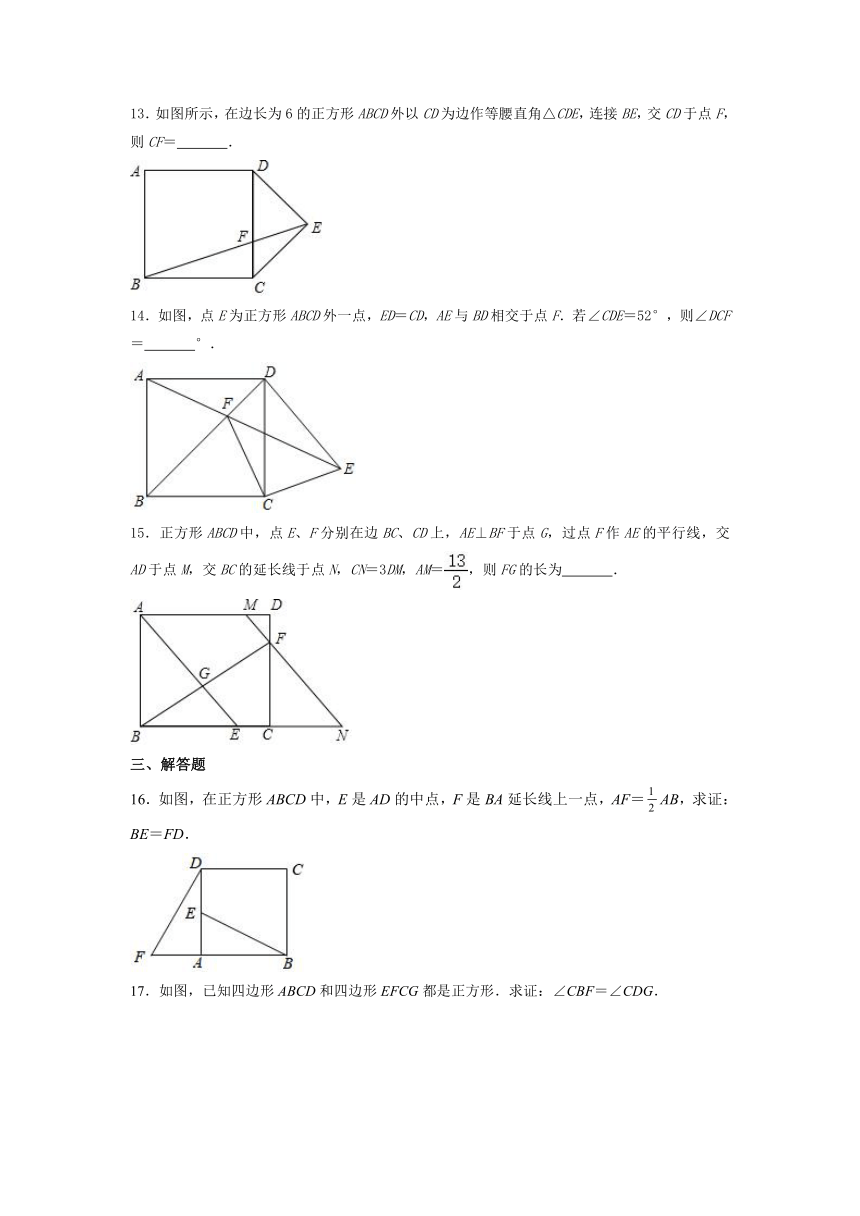
13.如图所示,在边长为6的正方形ABCD外以CD为边作等腰直角△CDE,连接BE,交CD于点F,则CF= .
14.如图,点E为正方形ABCD外一点,ED=CD,AE与BD相交于点F.若∠CDE=52°,则∠DCF= °.
15.正方形ABCD中,点E、F分别在边BC、CD上,AE⊥BF于点G,过点F作AE的平行线,交AD于点M,交BC的延长线于点N,CN=3DM,AM=,则FG的长为 .
三、解答题
16.如图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB,求证:BE=FD.
17.如图,已知四边形ABCD和四边形EFCG都是正方形.求证:∠CBF=∠CDG.
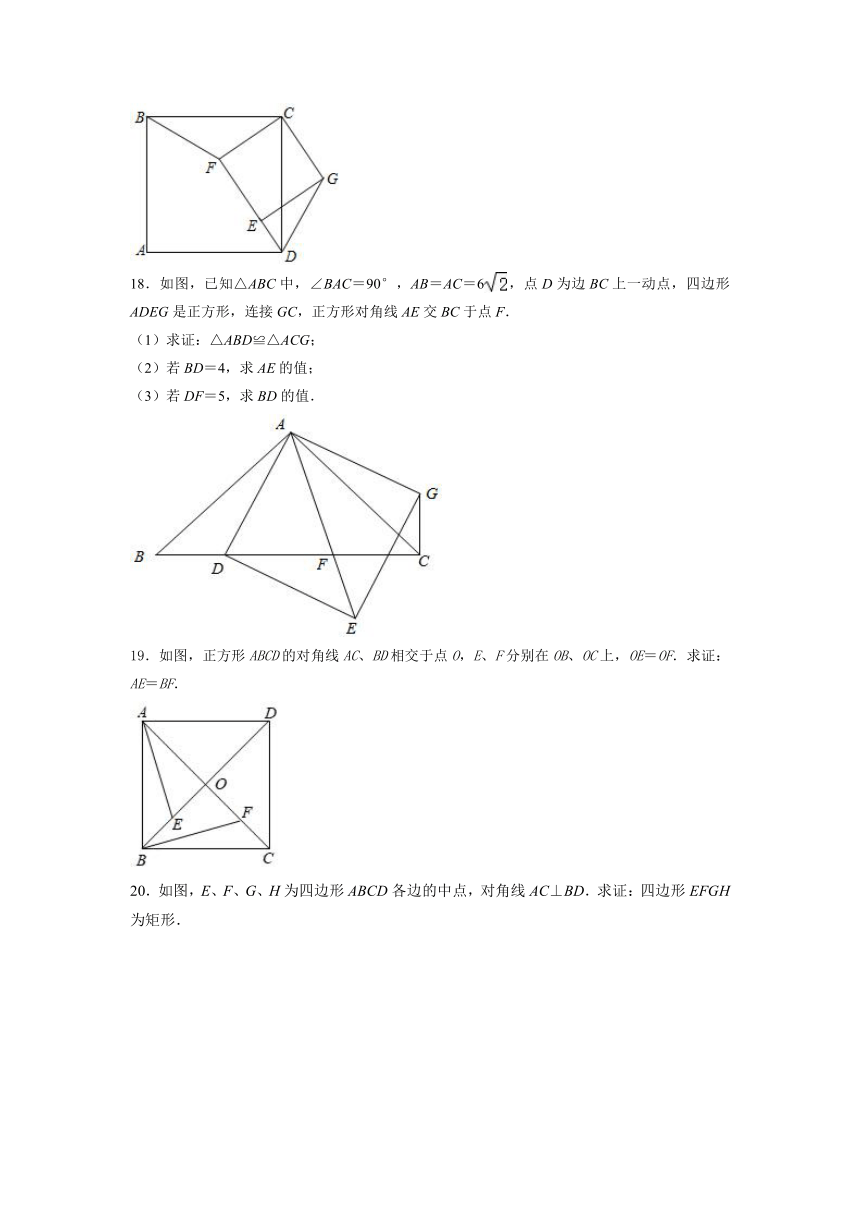
18.如图,已知△ABC中,∠BAC=90°,AB=AC=6,点D为边BC上一动点,四边形ADEG是正方形,连接GC,正方形对角线AE交BC于点F.
(1)求证:△ABD≌△ACG;
(2)若BD=4,求AE的值;
(3)若DF=5,求BD的值.
19.如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF.
20.如图,E、F、G、H为四边形ABCD各边的中点,对角线AC⊥BD.求证:四边形EFGH为矩形.
21.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=___时,四边形MENF是正方形(只写结论,不需证明).
【参考答案】
1.C 2.D 3.B 4.D 5.D 6.A 7.B 8.D 9.C 10.D
11.15°
12.4﹣2
13.2
14.19
15.5.2
16.证明:∵E是AD的中点,
∴AE=AD,
∵AF=AB,
∵正方形ABCD,
∴AB=AD,∠DAB=∠DAF=90°,
∴AF=AE,
∴Rt△ADF≌Rt△ABE(SAS),
∴BE=DF.
17.证明:∵四边形ABCD和四边形EFCG都是正方形,
∴CB=CD,CF=CG,∠BCD=∠FCG=90°,
∴∠BCF+∠DCF=∠DCF+∠DCG=90°,
∴∠BCF=∠DCG,
在△BCF和△DCG中,
,
∴△BCF≌△DCG(SAS),
∴∠CBF=∠CDG.
18.(1)证明:∵四边形ADEG是正方形,
∴AD=AG,∠DAG=90°,
∵∠BAC=90°,
∴∠BAC=∠DAG,
∴∠BAD+∠DAC=∠DAC+∠CAG,
∴∠BAD=∠CAG,
在△ABD和△ACG中,
,
∴△ABD≌△ACG(SAS).
(2)∵∠BAC=90°,AB=AC=6,
∴∠B=∠ACB=45°,
在Rt△ABC中,
∴BC===12,
∵BD=4,
∴DC=BC﹣BD=12﹣4=8,
由(1)知△ABD≌△ACG,
∴GC=BD=4,∠ACG=∠B=45°,
∴∠ACB+∠ACG=45°+45°=90°,
连接DG,
在Rt△DCG中,
DG===4,
∵四边形ADEG是正方形,
∴AE=DG,
∴AE=4.
(3)∵四边形ADEG是正方形,
∴AD=DE,∠ADE=90°,
∴∠DAE=∠AED=45°,
∵∠BAC=90°,
∴∠BAD+∠FAC=∠BAC﹣∠DAE=90°﹣45°=45°,
由(1)知△ABD≌△ACG,
∴∠BAD=∠CAG,AD=AG,BD=GC,
∴∠CAG+∠FAC=∠BAD+∠FAC=45°,
∴∠FAG=45°,
∴∠FAG=∠FAD,
在△DAF和△GAF中,
,
∴△DAF≌△GAF(SAS),
∴GF=DF,
∵DF=5,
∴GH=5,
设BD=x,则FC=12﹣5﹣x=7﹣x,
由(2)知∠FCG=90°,
在Rt△FCG中,
GC2+FC2=FG2,
∴x2+(7﹣x)2=52,
∴x1=3,x2=4,
∴BD的值为3或4.
19.证明:∵四边形ABCD为正方形,
∴OA=OB,AC⊥BD,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(SAS)
∴AE=BF.
20.证明:∵E、F分别为AB、BC的中点,
∴EF是△ABC的中位线,
∴EF=AC,EF//AC,
同理,GH=AC,GH//AC,FG=BD,
∴EF=GH,EF//GH,
∴四边形EFGH为平行四边形,
∵AC⊥BD,
∴∠HEF=90°,
∴平行四边形EFGH为矩形.
21.解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC.
∵M是AD的中点,
∴AM=DM,
∴△ABM≌△DCM(SAS),
∴BM=CM;
(2)四边形MENF是菱形,理由如下:
∵E、N、F分别是线段BM、BC、CM的中点,
∴,
∴四边形MENF是平行四边形,
同理可得:,
∵BM=CM,
∴EN=NF,
∴四边形MENF是菱形;
(3) 当AD:AB=2:1时,四边形MENF是正方形;
理由如下:
∵AD:AB=2:1,M是AD的中点,
∴AB=AM,
∴△ABM是等腰直角三角形,
∴∠AMB=45°,
同理:∠DMC=45°,
∴∠EMF=180°-45°-45°=90°,
由(2)得:四边形MENF是菱形,
∴四边形MENF是正方形.
故答案为:2:1
一、选择题
1.下列说法错误的是( )
A.平行四边形对边平行且相等 B.菱形的对角线平分一组对角
C.矩形的对角线互相垂直 D.正方形有四条对称轴
2.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90° B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD D.当 ABCD是菱形时,AB=AC
3.如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,则∠EAF=( )度
A.30° B.45° C.50° D.60°
4.如图,正方形ABCD的边长是4,点E是DC上一个点,且DE=1,P点在AC上移动,则PE+PD的最小值是( )
A.4 B.4.5 C.5.5 D.5
5.如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
6.有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )
A.4:9 B.2:3 C.1:2 D.1:
7.如图,在正方形ABCD所在平面内求一点P,使点P与正方形ABCD的任意两个顶点构成△PAB,△PBC,△PAD,△PCD均是等腰三角形,则满足上述条件的所有点P的个数为( )
A.8个 B.9个 C.10个 D.11个
8.如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.下列说法错误的是( )
A.若AC⊥BD,四边形ABCD是菱形
B.若AC=BD,四边形ABCD是矩形
C.若AB=BC且AC=BD,四边形ABCD是正方形
D.若∠ABC=90°,四边形ABCD是正方形
9.如图,在正方形ABCD中,对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM交CD于点N.若S四边形MOND=2,则BD的长为( )
A.2 B. C.4 D.2
10.如图,在等腰直角中,,以B为圆心,小于的长为半径画弧,分别交,于点E,F,分别以点E,F为圆心,大于的长为半径画弧,两弧交于点P,作射线交于点O,在射线上作,连接,.下列说法不正确的是( )
A. B. C. D.若四边形的周长为16,则
二、填空题
11.如图,P是正方形ABCD内一点,且PA=PD,PB=PC.若∠PBC=60°,则∠PAD=_____.
12.如图,正方形ABCD边长为2,点P在BC边上,DP交AC于点E,∠ADE=∠AED,则BP的长度是 .
13.如图所示,在边长为6的正方形ABCD外以CD为边作等腰直角△CDE,连接BE,交CD于点F,则CF= .
14.如图,点E为正方形ABCD外一点,ED=CD,AE与BD相交于点F.若∠CDE=52°,则∠DCF= °.
15.正方形ABCD中,点E、F分别在边BC、CD上,AE⊥BF于点G,过点F作AE的平行线,交AD于点M,交BC的延长线于点N,CN=3DM,AM=,则FG的长为 .
三、解答题
16.如图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB,求证:BE=FD.
17.如图,已知四边形ABCD和四边形EFCG都是正方形.求证:∠CBF=∠CDG.
18.如图,已知△ABC中,∠BAC=90°,AB=AC=6,点D为边BC上一动点,四边形ADEG是正方形,连接GC,正方形对角线AE交BC于点F.
(1)求证:△ABD≌△ACG;
(2)若BD=4,求AE的值;
(3)若DF=5,求BD的值.
19.如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF.
20.如图,E、F、G、H为四边形ABCD各边的中点,对角线AC⊥BD.求证:四边形EFGH为矩形.
21.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=___时,四边形MENF是正方形(只写结论,不需证明).
【参考答案】
1.C 2.D 3.B 4.D 5.D 6.A 7.B 8.D 9.C 10.D
11.15°
12.4﹣2
13.2
14.19
15.5.2
16.证明:∵E是AD的中点,
∴AE=AD,
∵AF=AB,
∵正方形ABCD,
∴AB=AD,∠DAB=∠DAF=90°,
∴AF=AE,
∴Rt△ADF≌Rt△ABE(SAS),
∴BE=DF.
17.证明:∵四边形ABCD和四边形EFCG都是正方形,
∴CB=CD,CF=CG,∠BCD=∠FCG=90°,
∴∠BCF+∠DCF=∠DCF+∠DCG=90°,
∴∠BCF=∠DCG,
在△BCF和△DCG中,
,
∴△BCF≌△DCG(SAS),
∴∠CBF=∠CDG.
18.(1)证明:∵四边形ADEG是正方形,
∴AD=AG,∠DAG=90°,
∵∠BAC=90°,
∴∠BAC=∠DAG,
∴∠BAD+∠DAC=∠DAC+∠CAG,
∴∠BAD=∠CAG,
在△ABD和△ACG中,
,
∴△ABD≌△ACG(SAS).
(2)∵∠BAC=90°,AB=AC=6,
∴∠B=∠ACB=45°,
在Rt△ABC中,
∴BC===12,
∵BD=4,
∴DC=BC﹣BD=12﹣4=8,
由(1)知△ABD≌△ACG,
∴GC=BD=4,∠ACG=∠B=45°,
∴∠ACB+∠ACG=45°+45°=90°,
连接DG,
在Rt△DCG中,
DG===4,
∵四边形ADEG是正方形,
∴AE=DG,
∴AE=4.
(3)∵四边形ADEG是正方形,
∴AD=DE,∠ADE=90°,
∴∠DAE=∠AED=45°,
∵∠BAC=90°,
∴∠BAD+∠FAC=∠BAC﹣∠DAE=90°﹣45°=45°,
由(1)知△ABD≌△ACG,
∴∠BAD=∠CAG,AD=AG,BD=GC,
∴∠CAG+∠FAC=∠BAD+∠FAC=45°,
∴∠FAG=45°,
∴∠FAG=∠FAD,
在△DAF和△GAF中,
,
∴△DAF≌△GAF(SAS),
∴GF=DF,
∵DF=5,
∴GH=5,
设BD=x,则FC=12﹣5﹣x=7﹣x,
由(2)知∠FCG=90°,
在Rt△FCG中,
GC2+FC2=FG2,
∴x2+(7﹣x)2=52,
∴x1=3,x2=4,
∴BD的值为3或4.
19.证明:∵四边形ABCD为正方形,
∴OA=OB,AC⊥BD,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(SAS)
∴AE=BF.
20.证明:∵E、F分别为AB、BC的中点,
∴EF是△ABC的中位线,
∴EF=AC,EF//AC,
同理,GH=AC,GH//AC,FG=BD,
∴EF=GH,EF//GH,
∴四边形EFGH为平行四边形,
∵AC⊥BD,
∴∠HEF=90°,
∴平行四边形EFGH为矩形.
21.解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC.
∵M是AD的中点,
∴AM=DM,
∴△ABM≌△DCM(SAS),
∴BM=CM;
(2)四边形MENF是菱形,理由如下:
∵E、N、F分别是线段BM、BC、CM的中点,
∴,
∴四边形MENF是平行四边形,
同理可得:,
∵BM=CM,
∴EN=NF,
∴四边形MENF是菱形;
(3) 当AD:AB=2:1时,四边形MENF是正方形;
理由如下:
∵AD:AB=2:1,M是AD的中点,
∴AB=AM,
∴△ABM是等腰直角三角形,
∴∠AMB=45°,
同理:∠DMC=45°,
∴∠EMF=180°-45°-45°=90°,
由(2)得:四边形MENF是菱形,
∴四边形MENF是正方形.
故答案为:2:1
