2021-2022学年人教版八年级下册数学18.2.3正方形同步测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学18.2.3正方形同步测试(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 297.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 00:00:00 | ||
图片预览

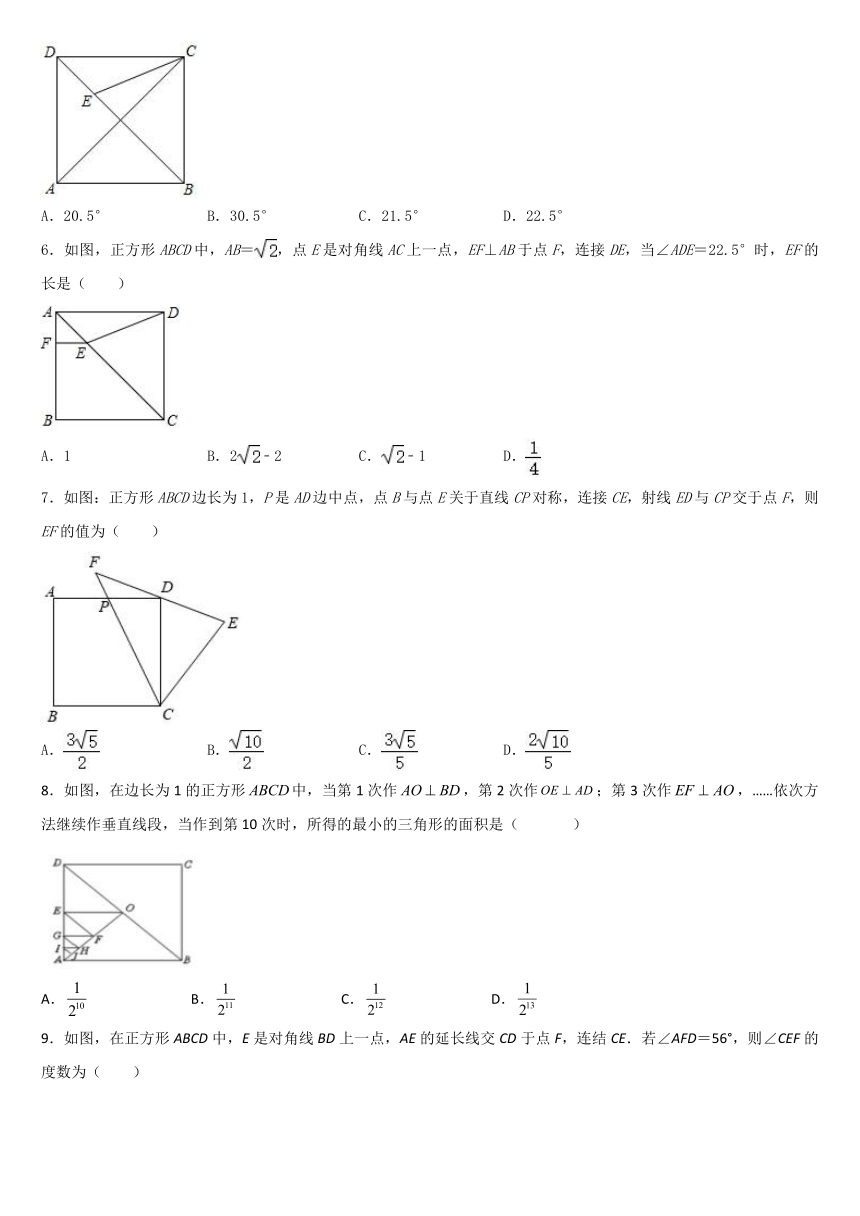

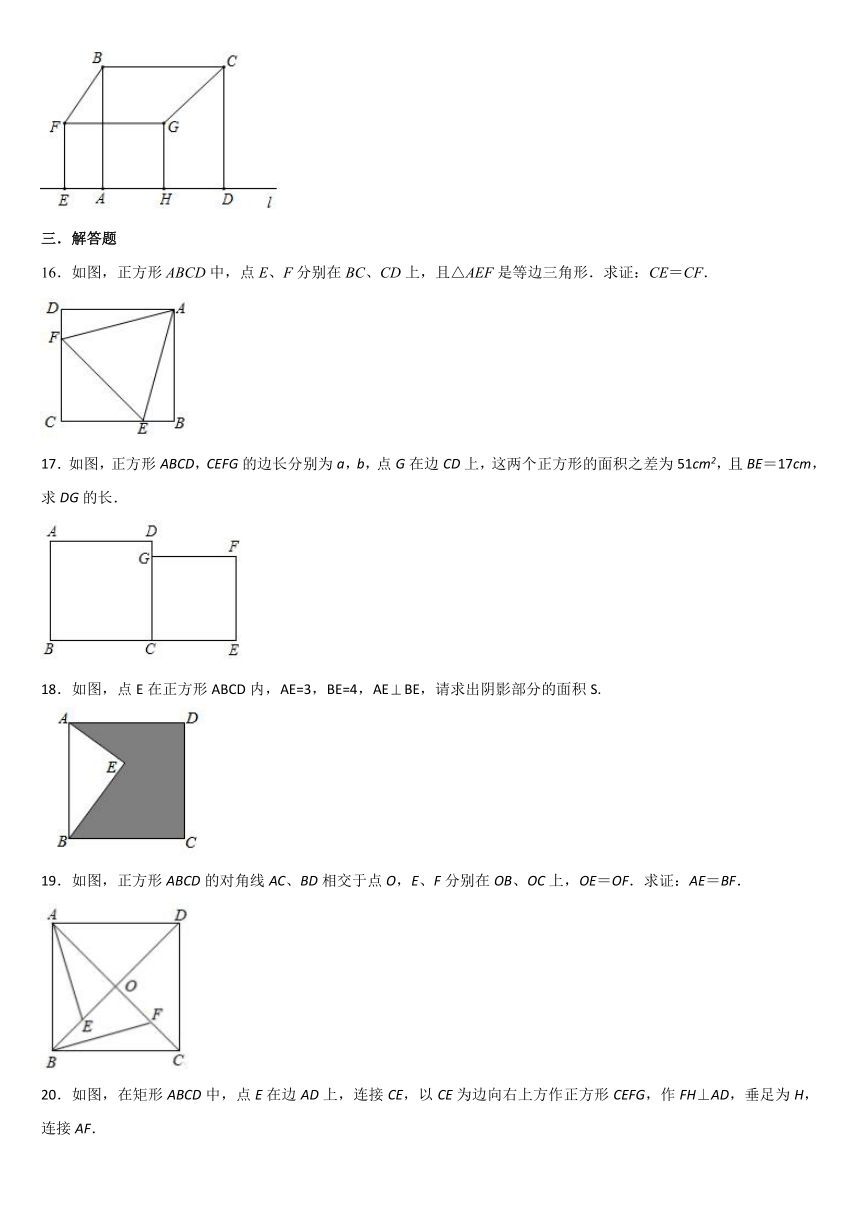
文档简介
18.2.3正方形 同步测试
一.选择题
1.下列对正方形的描述错误的是( )
A.正方形的四个角都是直角
B.正方形的对角线互相垂直
C.对角线相等的平行四边形是正方形
D.邻边相等的矩形是正方形
2.如图,在正方形ABCD中,E、F是对角线BD上的点,AB=BF=DE,则∠EAF的度数为( )
A.22.5° B.30° C.45° D.67.5°
3.如图,点P是线段AB上任意一点,在AB同侧作正方形ACDP、正方形PEFB,连接DF、PF,已知AB=10,当△PDF的面积为8时,AP的长为( )
A.2 B.8 C.2或8 D.4
4.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),则下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.
其中说法正确的是( )
A.②③ B.①②③ C.②④ D.①②④
5.如图,在正方形ABCD中,E为对角线BD上一点,且BE=BC,则∠ACE=( )
A.20.5° B.30.5° C.21.5° D.22.5°
6.如图,正方形ABCD中,AB=,点E是对角线AC上一点,EF⊥AB于点F,连接DE,当∠ADE=22.5°时,EF的长是( )
A.1 B.2﹣2 C.﹣1 D.
7.如图:正方形ABCD边长为1,P是AD边中点,点B与点E关于直线CP对称,连接CE,射线ED与CP交于点F,则EF的值为( )
A. B. C. D.
8.如图,在边长为1的正方形中,当第1次作,第2次作;第3次作,……依次方法继续作垂直线段,当作到第10次时,所得的最小的三角形的面积是( )
A. B. C. D.
9.如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连结CE.若∠AFD=56°,则∠CEF的度数为( )
A.22° B.24° C.26° D.28°
10.如图,已知四边形是平行四边形,对角线、交于点,下列叙述错误的是( )
A.当时,它是菱形 B.当时,它是菱形
C.当时,它是矩形 D.当时,它是正方形
二.填空题
11.一个正方形的对角线长为2,则其面积为 .
12.如图,正方形ABCD的边长为4,E是BC延长线上一点,P是∠DCE平分线上任意一点则△PBD的面积是 ___.
13.如图,点M是的中点,点P在上.分别以,为边,作正方形和正方形,连接和,设,,且,.则图中阴影部分的面积为__________.
14.如图,在菱形中,,,点,同时由,两点出发,分别沿,方向向点匀速运动,点的运动速度为,点的运动速度为,点到达点后,点与点同时停止运动.若运动时间为秒时,为等边三角形,则的值为__________.
15.如图,正方形与矩形在直线的同侧,边,在直线上,且,,.保持正方形不动,将矩形沿直线左右移动,连接,,则的最小值为______.
三.解答题
16.如图,正方形ABCD中,点E、F分别在BC、CD上,且△AEF是等边三角形.求证:CE=CF.
17.如图,正方形ABCD,CEFG的边长分别为a,b,点G在边CD上,这两个正方形的面积之差为51cm2,且BE=17cm,求DG的长.
18.如图,点E在正方形ABCD内,AE=3,BE=4,AEBE,请求出阴影部分的面积S.
19.如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF.
20.如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)若AB=3,AD=5,当AE=1时,求∠FAD的度数.
参考答案
1.C 2.C 3.C 4.B 5.D 6.C 7.D 8.B 9.A 10.D
11.2.
12.
13.90
14.
15.
16.证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠B=90°,
∵△AEF是等边三角形,
∴AF=AE,
在Rt△ADF和Rt△ABE中,
,
∴Rt△ADF≌Rt△ABE(HL),
∴DF=BE,
∴CE=CF.
17.解:∵四边形ABCD,CEFG都是正方形,
设BC为x,CE为y,
可得:,
解得:x y=3,
∴DG=CD CG=BC CE=3(cm).
18.解:∵AE⊥BE,
∴∠AEB=90°,
在RtΔABE中,由勾股定理得AE +BE =AB ,
∴3 +4 =AB ,
∴ AB=5 ,
∴ =5 - =25-6=19.
19.∵四边形ABCD为正方形,
∴OA=OB,AC⊥BD,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(SAS)
∴AE=BF.
20.(1)证明:∵四边形CEFG是正方形,
∴CE=EF,
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE,
在△FEH和△ECD中,
,
∴△FEH≌△ECD(AAS),
∴FH=ED;
(2)解:∵在矩形ABCD中,AB=3,AD=5,
∴CD=AB=3,
∵AE=1,
∴DE=4,
∵△FEH≌△ECD,
∴FH=DE=4,EH=CD=3,
∴AH=4,
∴AH=FH,
∵∠FHE=90°,
∴∠FAD=45°.
一.选择题
1.下列对正方形的描述错误的是( )
A.正方形的四个角都是直角
B.正方形的对角线互相垂直
C.对角线相等的平行四边形是正方形
D.邻边相等的矩形是正方形
2.如图,在正方形ABCD中,E、F是对角线BD上的点,AB=BF=DE,则∠EAF的度数为( )
A.22.5° B.30° C.45° D.67.5°
3.如图,点P是线段AB上任意一点,在AB同侧作正方形ACDP、正方形PEFB,连接DF、PF,已知AB=10,当△PDF的面积为8时,AP的长为( )
A.2 B.8 C.2或8 D.4
4.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),则下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.
其中说法正确的是( )
A.②③ B.①②③ C.②④ D.①②④
5.如图,在正方形ABCD中,E为对角线BD上一点,且BE=BC,则∠ACE=( )
A.20.5° B.30.5° C.21.5° D.22.5°
6.如图,正方形ABCD中,AB=,点E是对角线AC上一点,EF⊥AB于点F,连接DE,当∠ADE=22.5°时,EF的长是( )
A.1 B.2﹣2 C.﹣1 D.
7.如图:正方形ABCD边长为1,P是AD边中点,点B与点E关于直线CP对称,连接CE,射线ED与CP交于点F,则EF的值为( )
A. B. C. D.
8.如图,在边长为1的正方形中,当第1次作,第2次作;第3次作,……依次方法继续作垂直线段,当作到第10次时,所得的最小的三角形的面积是( )
A. B. C. D.
9.如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连结CE.若∠AFD=56°,则∠CEF的度数为( )
A.22° B.24° C.26° D.28°
10.如图,已知四边形是平行四边形,对角线、交于点,下列叙述错误的是( )
A.当时,它是菱形 B.当时,它是菱形
C.当时,它是矩形 D.当时,它是正方形
二.填空题
11.一个正方形的对角线长为2,则其面积为 .
12.如图,正方形ABCD的边长为4,E是BC延长线上一点,P是∠DCE平分线上任意一点则△PBD的面积是 ___.
13.如图,点M是的中点,点P在上.分别以,为边,作正方形和正方形,连接和,设,,且,.则图中阴影部分的面积为__________.
14.如图,在菱形中,,,点,同时由,两点出发,分别沿,方向向点匀速运动,点的运动速度为,点的运动速度为,点到达点后,点与点同时停止运动.若运动时间为秒时,为等边三角形,则的值为__________.
15.如图,正方形与矩形在直线的同侧,边,在直线上,且,,.保持正方形不动,将矩形沿直线左右移动,连接,,则的最小值为______.
三.解答题
16.如图,正方形ABCD中,点E、F分别在BC、CD上,且△AEF是等边三角形.求证:CE=CF.
17.如图,正方形ABCD,CEFG的边长分别为a,b,点G在边CD上,这两个正方形的面积之差为51cm2,且BE=17cm,求DG的长.
18.如图,点E在正方形ABCD内,AE=3,BE=4,AEBE,请求出阴影部分的面积S.
19.如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF.
20.如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)若AB=3,AD=5,当AE=1时,求∠FAD的度数.
参考答案
1.C 2.C 3.C 4.B 5.D 6.C 7.D 8.B 9.A 10.D
11.2.
12.
13.90
14.
15.
16.证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠B=90°,
∵△AEF是等边三角形,
∴AF=AE,
在Rt△ADF和Rt△ABE中,
,
∴Rt△ADF≌Rt△ABE(HL),
∴DF=BE,
∴CE=CF.
17.解:∵四边形ABCD,CEFG都是正方形,
设BC为x,CE为y,
可得:,
解得:x y=3,
∴DG=CD CG=BC CE=3(cm).
18.解:∵AE⊥BE,
∴∠AEB=90°,
在RtΔABE中,由勾股定理得AE +BE =AB ,
∴3 +4 =AB ,
∴ AB=5 ,
∴ =5 - =25-6=19.
19.∵四边形ABCD为正方形,
∴OA=OB,AC⊥BD,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(SAS)
∴AE=BF.
20.(1)证明:∵四边形CEFG是正方形,
∴CE=EF,
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE,
在△FEH和△ECD中,
,
∴△FEH≌△ECD(AAS),
∴FH=ED;
(2)解:∵在矩形ABCD中,AB=3,AD=5,
∴CD=AB=3,
∵AE=1,
∴DE=4,
∵△FEH≌△ECD,
∴FH=DE=4,EH=CD=3,
∴AH=4,
∴AH=FH,
∵∠FHE=90°,
∴∠FAD=45°.
