2021-2022学年人教版数学八年级下册18.2.2菱形同步习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册18.2.2菱形同步习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 197.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 18:18:20 | ||
图片预览

文档简介
18.2.2菱形 同步习题
一.选择题
1.下列关系中,是菱形的性质但不是平行四边形的性质的是( )
A.对角线垂直 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
2.如图,菱形的对角线相交于点O,点E是边的中点,若,则的长是( )
A.6 B.5 C.4 D.3
3.如图,菱形的对角线、相交于点,,,为过点的一条直线,则图中阴影部分的面积为( )
A.4 B.6 C.8 D.12
4.如图,在的两边上分别截取,,使;再分别以点A,B为圆心,长为半径作弧,两弧交于点C;再连接AC,BC,AB,OC.若,,则四边形的面积是( )
A. B.8 C.4 D.
5.如图,四边形ABCD为菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是( )
A.20° B.25° C.30° D.35°
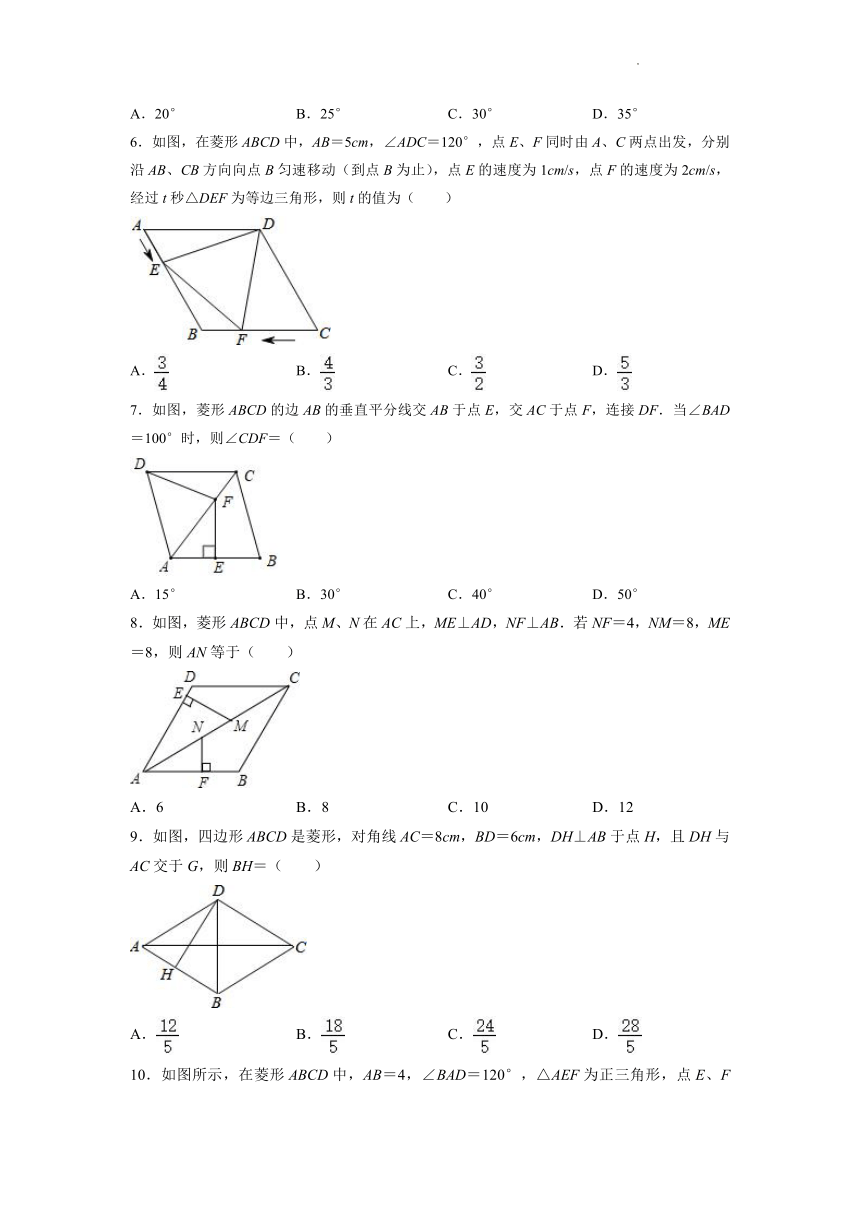
6.如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A. B. C. D.
7.如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF.当∠BAD=100°时,则∠CDF=( )
A.15° B.30° C.40° D.50°
8.如图,菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB.若NF=4,NM=8,ME=8,则AN等于( )
A.6 B.8 C.10 D.12
9.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则BH=( )
A. B. C. D.
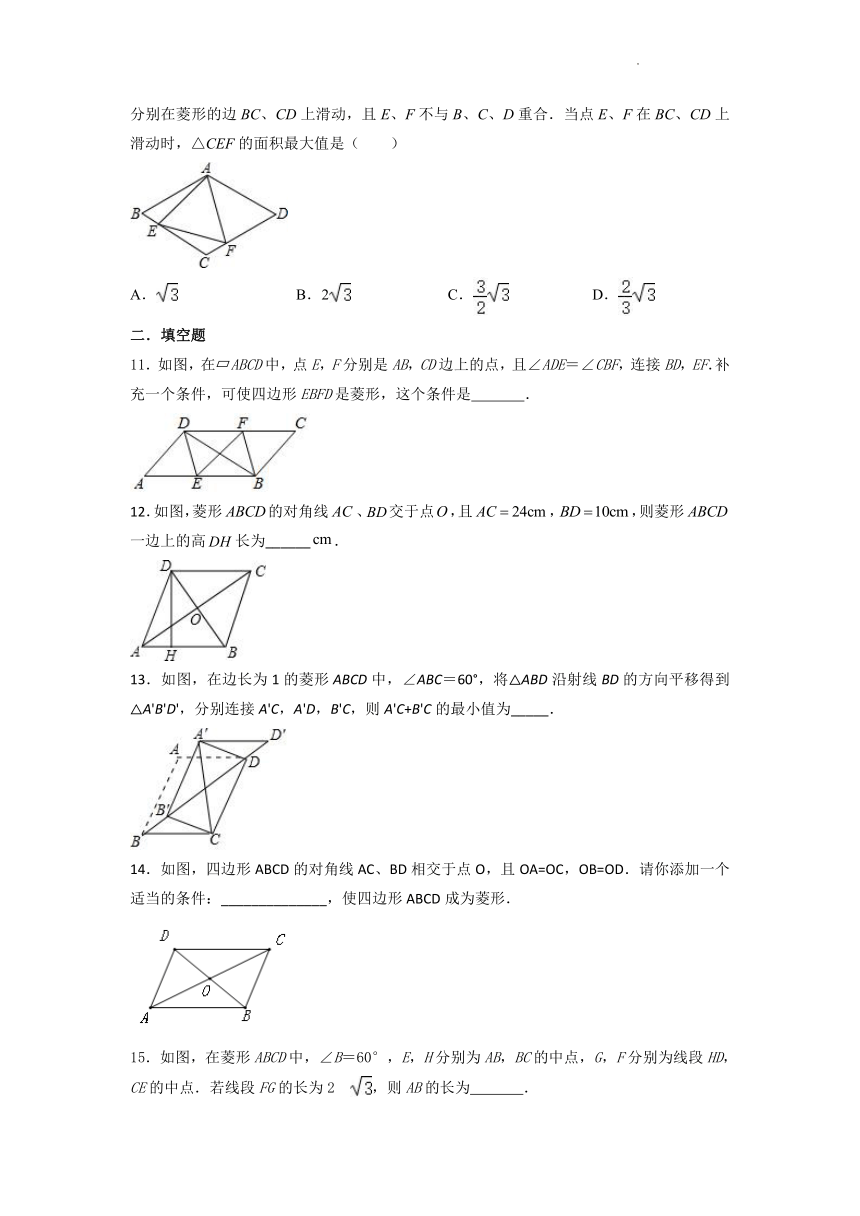
10.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( )
A. B.2 C. D.
二.填空题
11.如图,在 ABCD中,点E,F分别是AB,CD边上的点,且∠ADE=∠CBF,连接BD,EF.补充一个条件,可使四边形EBFD是菱形,这个条件是 .
12.如图,菱形的对角线、交于点,且,,则菱形一边上的高长为______.
13.如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为_____.
14.如图,四边形ABCD的对角线AC、BD相交于点O,且OA=OC,OB=OD.请你添加一个适当的条件:______________,使四边形ABCD成为菱形.
15.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2 ,则AB的长为 .
三.解答题
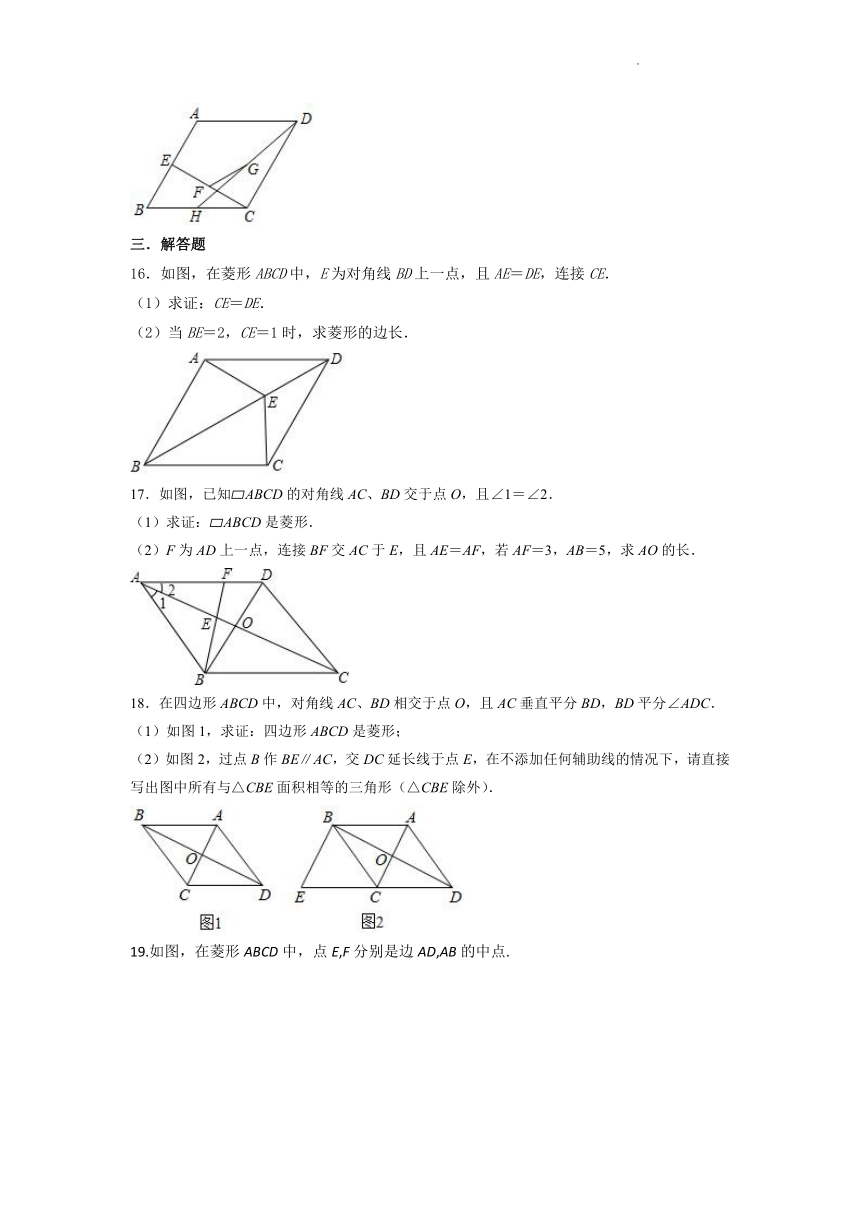
16.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
17.如图,已知 ABCD的对角线AC、BD交于点O,且∠1=∠2.
(1)求证: ABCD是菱形.
(2)F为AD上一点,连接BF交AC于E,且AE=AF,若AF=3,AB=5,求AO的长.
18.在四边形ABCD中,对角线AC、BD相交于点O,且AC垂直平分BD,BD平分∠ADC.
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,过点B作BE∥AC,交DC延长线于点E,在不添加任何辅助线的情况下,请直接写出图中所有与△CBE面积相等的三角形(△CBE除外).
19.如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.
(1)求证:;
(2)若,求菱形ABCD的面积.
20.如图,已知在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
参考答案
一.选择题
1.A 2.A 3.B 4.C 5.B 6.D 7.D 8.B 9.B 10.A
11.:BD⊥EF.
12.
13.
14.AB=AD.
6
16.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BH=BD=,EH=BE﹣BH=2﹣=,
在Rt△AHE中,由勾股定理得:AH===,
在Rt△AHB中,由勾股定理得:AB===,
∴菱形的边长为.
17.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,OB=OD=BD=3,
∴OA===4,
∴AC=2OA=8,
∴菱形ABCD的面积=AC×BD=×8×6=24,
∵CE⊥AB,
∴菱形ABCD的面积=AB×CE=5CE=24,
∴CE=.
18.(1)证明:∵四边形ABCD是菱形,
∴OA=OC=AC,
∵2DE=AC,
∴DE=OA,
又∵DE∥AC,
∴四边形OADE是平行四边形,
∴AF=EF;
(2)解:连接CE,
∵DE∥OC,DE=OC,
∴四边形OCED是平行四边形,
又∵菱形ABCD,
∴AC⊥BD,
∴四边形OCED是矩形,
∴∠OCE=90°,
又∵AB=2DE=AC,
∴△ABC为等边三角形,
∵在菱形ABCD中,∠ABC=60°,
∴AC=AB=2,AO=AC=1,
∴在矩形OCED中,CE=OD==,
∴在Rt△ACE中,
AE==.
19答案:(1)证明:由图可知,BD垂直平分AC,且.所以,四边形ABCD为菱形.
(2),且BD平分AC.
.
在中,.
.
BD的长为6.
20. (1)解:∵四边形ABCD是菱形,
∴CB=CD,AB∥CD,
∴∠1=∠ACD.
∵∠1=∠2,
∴∠2=∠ACD,
∴MC=MD.
∵ME⊥CD,
∴CD=2CE=2,
∴BC=CD=2.
(2)证明:如图,延长DF交AB的延长线于点G.
∵四边形ABCD是菱形,
∴∠BCA=∠DCA,BC=CD.
∵BC=2CF,CD=2CE,
∴CE=CF.
∵CM=CM,
∴△CEM≌△CFM,
∴ME=MF.
∵AB∥CD,
∴∠2=∠G,∠BCD=∠GBF.
∵CF=BF,
∴△CDF≌△BGF,
∴DF=GF.
∵∠1=∠2,∠G=∠2,
∴∠1=∠G,
∴AM=GM=MF+GF=DF+ME.
一.选择题
1.下列关系中,是菱形的性质但不是平行四边形的性质的是( )
A.对角线垂直 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
2.如图,菱形的对角线相交于点O,点E是边的中点,若,则的长是( )
A.6 B.5 C.4 D.3
3.如图,菱形的对角线、相交于点,,,为过点的一条直线,则图中阴影部分的面积为( )
A.4 B.6 C.8 D.12
4.如图,在的两边上分别截取,,使;再分别以点A,B为圆心,长为半径作弧,两弧交于点C;再连接AC,BC,AB,OC.若,,则四边形的面积是( )
A. B.8 C.4 D.
5.如图,四边形ABCD为菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是( )
A.20° B.25° C.30° D.35°
6.如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A. B. C. D.
7.如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF.当∠BAD=100°时,则∠CDF=( )
A.15° B.30° C.40° D.50°
8.如图,菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB.若NF=4,NM=8,ME=8,则AN等于( )
A.6 B.8 C.10 D.12
9.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则BH=( )
A. B. C. D.
10.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( )
A. B.2 C. D.
二.填空题
11.如图,在 ABCD中,点E,F分别是AB,CD边上的点,且∠ADE=∠CBF,连接BD,EF.补充一个条件,可使四边形EBFD是菱形,这个条件是 .
12.如图,菱形的对角线、交于点,且,,则菱形一边上的高长为______.
13.如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为_____.
14.如图,四边形ABCD的对角线AC、BD相交于点O,且OA=OC,OB=OD.请你添加一个适当的条件:______________,使四边形ABCD成为菱形.
15.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2 ,则AB的长为 .
三.解答题
16.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
17.如图,已知 ABCD的对角线AC、BD交于点O,且∠1=∠2.
(1)求证: ABCD是菱形.
(2)F为AD上一点,连接BF交AC于E,且AE=AF,若AF=3,AB=5,求AO的长.
18.在四边形ABCD中,对角线AC、BD相交于点O,且AC垂直平分BD,BD平分∠ADC.
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,过点B作BE∥AC,交DC延长线于点E,在不添加任何辅助线的情况下,请直接写出图中所有与△CBE面积相等的三角形(△CBE除外).
19.如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.
(1)求证:;
(2)若,求菱形ABCD的面积.
20.如图,已知在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
参考答案
一.选择题
1.A 2.A 3.B 4.C 5.B 6.D 7.D 8.B 9.B 10.A
11.:BD⊥EF.
12.
13.
14.AB=AD.
6
16.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BH=BD=,EH=BE﹣BH=2﹣=,
在Rt△AHE中,由勾股定理得:AH===,
在Rt△AHB中,由勾股定理得:AB===,
∴菱形的边长为.
17.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,OB=OD=BD=3,
∴OA===4,
∴AC=2OA=8,
∴菱形ABCD的面积=AC×BD=×8×6=24,
∵CE⊥AB,
∴菱形ABCD的面积=AB×CE=5CE=24,
∴CE=.
18.(1)证明:∵四边形ABCD是菱形,
∴OA=OC=AC,
∵2DE=AC,
∴DE=OA,
又∵DE∥AC,
∴四边形OADE是平行四边形,
∴AF=EF;
(2)解:连接CE,
∵DE∥OC,DE=OC,
∴四边形OCED是平行四边形,
又∵菱形ABCD,
∴AC⊥BD,
∴四边形OCED是矩形,
∴∠OCE=90°,
又∵AB=2DE=AC,
∴△ABC为等边三角形,
∵在菱形ABCD中,∠ABC=60°,
∴AC=AB=2,AO=AC=1,
∴在矩形OCED中,CE=OD==,
∴在Rt△ACE中,
AE==.
19答案:(1)证明:由图可知,BD垂直平分AC,且.所以,四边形ABCD为菱形.
(2),且BD平分AC.
.
在中,.
.
BD的长为6.
20. (1)解:∵四边形ABCD是菱形,
∴CB=CD,AB∥CD,
∴∠1=∠ACD.
∵∠1=∠2,
∴∠2=∠ACD,
∴MC=MD.
∵ME⊥CD,
∴CD=2CE=2,
∴BC=CD=2.
(2)证明:如图,延长DF交AB的延长线于点G.
∵四边形ABCD是菱形,
∴∠BCA=∠DCA,BC=CD.
∵BC=2CF,CD=2CE,
∴CE=CF.
∵CM=CM,
∴△CEM≌△CFM,
∴ME=MF.
∵AB∥CD,
∴∠2=∠G,∠BCD=∠GBF.
∵CF=BF,
∴△CDF≌△BGF,
∴DF=GF.
∵∠1=∠2,∠G=∠2,
∴∠1=∠G,
∴AM=GM=MF+GF=DF+ME.
