4.2.3直线与圆的方程的应用
文档属性
| 名称 | 4.2.3直线与圆的方程的应用 |  | |
| 格式 | zip | ||
| 文件大小 | 707.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-09 14:37:21 | ||
图片预览






文档简介
课件33张PPT。4.2.3直线与圆的方程的应用湖南省耒阳市振兴学校
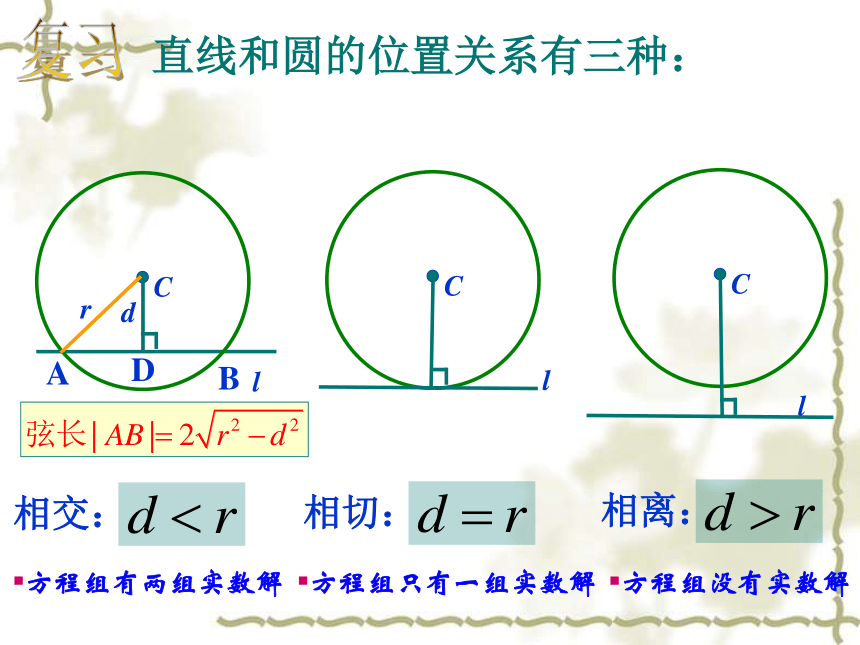
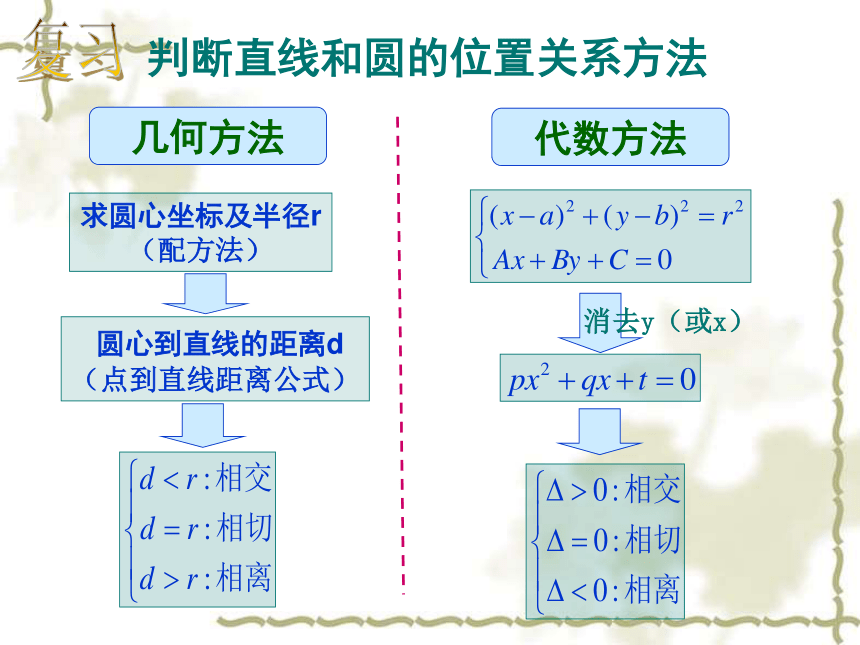
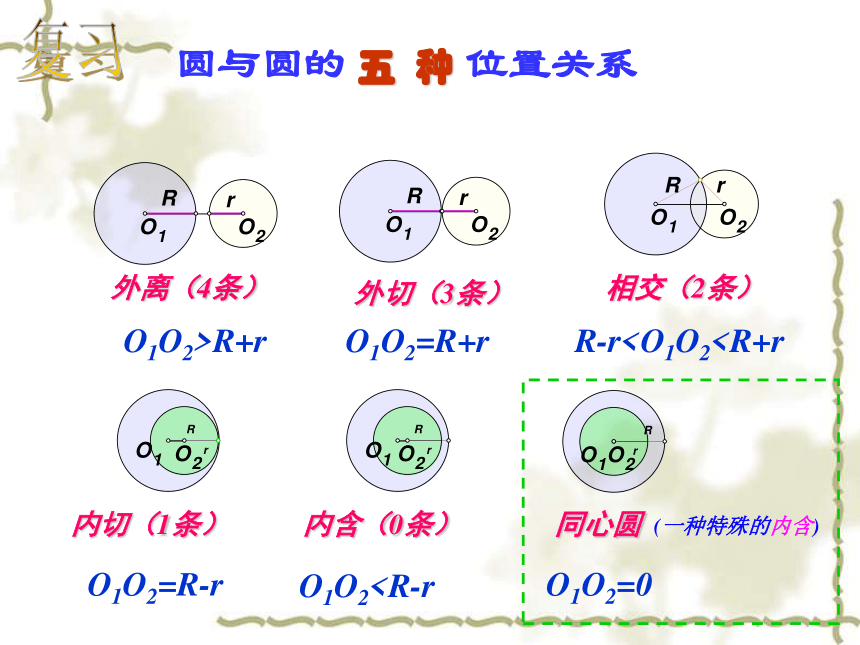
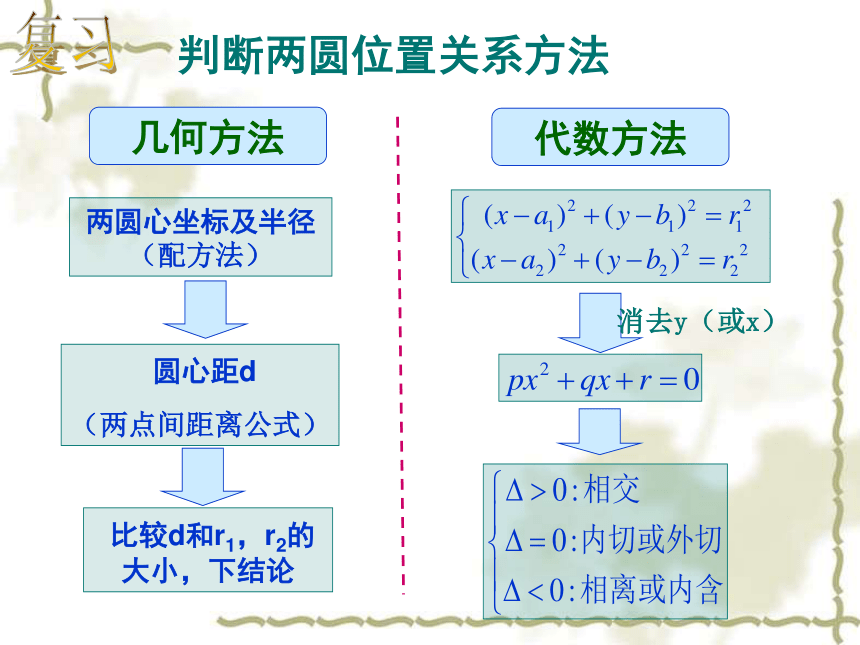
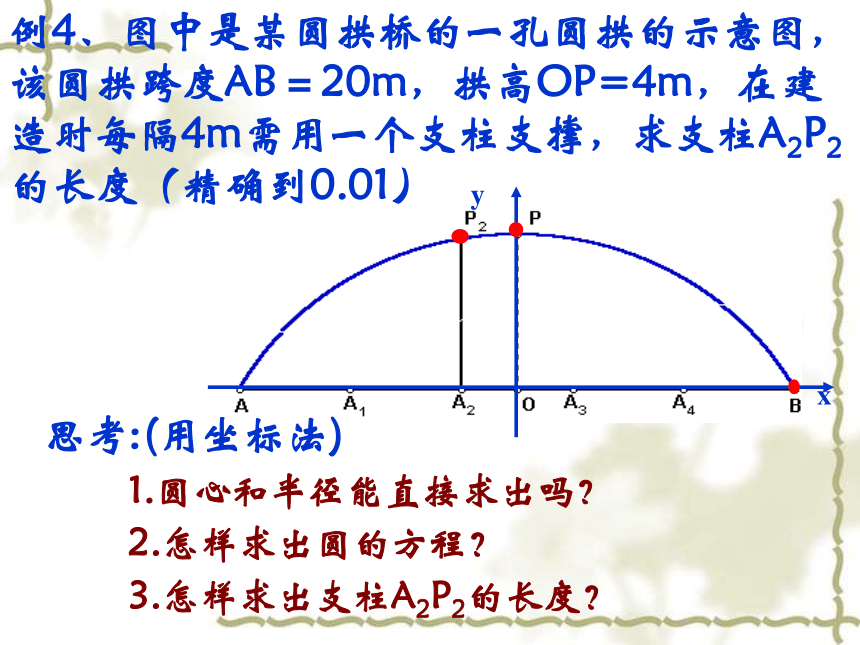
高中数学老师欧阳文丰制作(1)理解直线与圆、圆与圆的位置关系的几何性质(3)利用数形结合的思想解决数学和实际问题(2)通过建立适当的平面直角坐标系,利用坐标法解决直线与圆的问题直线和圆的位置关系有三种:Cldr相交:l相切:相离:方程组有两组实数解方程组只有一组实数解方程组没有实数解ABD复习判断直线和圆的位置关系方法几何方法求圆心坐标及半径r(配方法) 圆心到直线的距离d (点到直线距离公式)代数方法 消去y(或x)复习圆与圆的 位置关系外离(4条)O1O2>R+rO1O2=R+rR-r(两点间距离公式) 比较d和r1,r2的大小,下结论代数方法 消去y(或x)复习问题提出 通过直线与圆的方程,可以确定直线与圆、圆和圆的位置关系,对于生产、生活实践以及平面几何中与直线和圆有关的问题,我们可以建立直角坐标系,通过直线与圆的方程,将其转化为代数问题来解决.对此,我们必须掌握解决问题的基本思想和方法.例4、图中是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01)思考:(用坐标法)
1.圆心和半径能直接求出吗?
2.怎样求出圆的方程?
3.怎样求出支柱A2P2的长度?例4。如图是某圆拱桥的一孔圆拱示意图.该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需要用一个支柱支撑,求支柱A2P2 的长度(精确到0.01m).
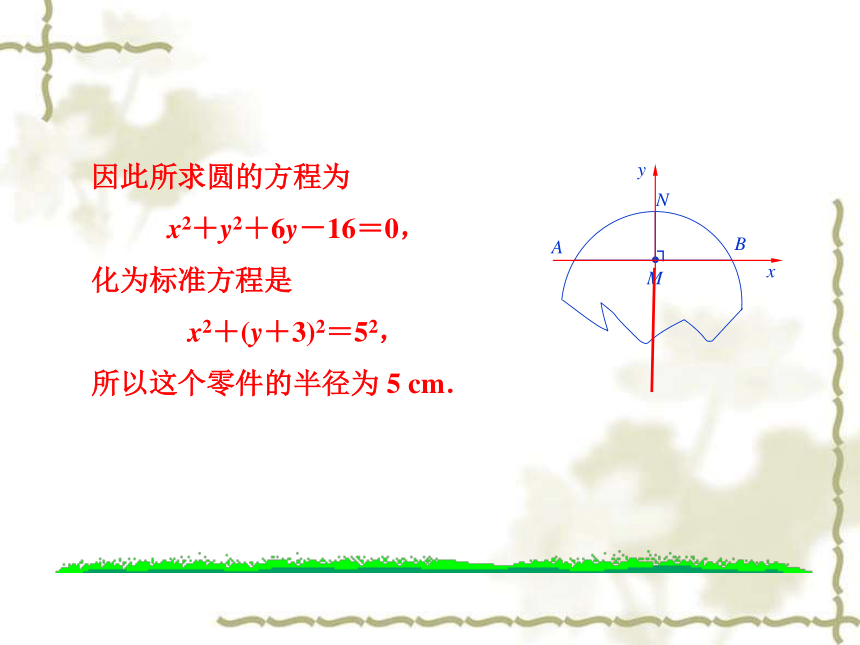
练习:某次生产中,一个圆形的零件损坏了,只剩下了如图所示的一部分.现在陈师傅所在的车间准备重新做一个这样的零件,为了获得这个圆形零件的半径,陈师傅在零件上画了一条线段 AB,并作出了 AB 的垂直平分线 MN,而且测得 AB=8 cm,MN=2 cm.根据已有数据,试帮陈师傅求出这个零件的半径.解:以 AB 中点 M 为原点,建立如图所示的平面直角坐标系,由已知有 A(-4,0),B(4,0),N(0,2).
设过 A,B,N 的圆的方程为
x2+y2+Dx+Ey+F=0,
代入 A,B,N 的坐标,可得 解得 因此所求圆的方程为
x2+y2+6y-16=0,
化为标准方程是
x2+(y+3)2=52,
所以这个零件的半径为 5 cm.E例5、已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半.(a,0)(0,b)(c,0)(0,d)证明:过四边形ABCD外接圆的圆心O’ 分别作AC,BD,AD的垂线,垂足分别为
M,N,E,则M,N,E分别是线段AC,BD,AD的中点。由中点坐标公式,得
所以 小结:坐标法解决平面几何问题的“三步曲” 。一、建立适当的平面直角坐标系,用坐标和 方程 表示问题中的几何元素,将平面几何问题转化为代数问题;
二、通过代数运算,解决代数问题;
三、将代数运算结果“翻译” 成几何结论。
这是坐标法解决平面几何问题的“三步曲” ,又简称为“一建二算三译”。 等边三角形ABC中,点D,E分别在边BC,AC上,且有AD,BE相交于点P.求证:解:如下图,建立直角坐标系,使A?B?O三点的坐标分别为
A(4,0)?B(0,3)?O(0,0).解:以B为原点,BC边所在直线为轴,线段 为单位长,建立如图所示的坐标系,则直线AD的方程为直线BE的方程为解以上两方程联立的方程组,得所以点P的坐标是直线PC的斜率因为所以例6:已知△AOB中,|OB|=3,|OA|=4,|AB|=5,点P是△ABO内切圆上一点,求以|PA|?|PB|?|PO|为直径的三个圆面积之和的最大值与最小值.
分析:三个圆面积之和的最值问题实质上是求|PA|2+|PB|2+|PO|2的最值.
由于P是△ABO内切圆上的点,若想找到P点坐标,必须先从△ABO内切圆的方程入手.易求得△ABO的内切点半径r=1,圆心(1,1).
故内切圆的方程是
(x-1)2+(y-1)2=1.
化简为x2+y2-2x-2y+1=0,①
设P(x,y),则
|PA|2+|PB|2+|PO|2
=(x-4)2+y2+x2+(y-3)2+x2+y2
=3x2+3y2-8x-6y+25.②例7.已知实数x,y满足方程x2+y2-4x+1=0,
(1)求 的最值;
(2)求y-x的最值;
(3)求x2+y2的最值.
解:(1)∵圆的标准方程为(x-2)2+y2=3,其圆心为(2,0),半径为 设 即y=kx.
当直线y=kx与圆相切时,斜率k取最大值和最小值.此时
解得k=±
∴ 的最大值为 最小值为 (2)设y-x=b,即y=x+b.当y=x+b与圆相切时,纵截距b取得最大值和最小值,此时
即b=-2± ∴y-x的最大值为 最小值为-2- (3)x2+y2表示圆上一点与原点距离的平方,由平面几何知识可知,它在过原点的连心线与圆的交点处取得最大值和最小值.又圆心到原点的距离为2,
∴x2+y2的最大值为 最小值为拓展提高
练习1、求直线l: 2x-y-2=0被圆C: (x-3)2+y2=0所截得的弦长.2、某圆拱桥的水面跨度20 m,拱高4 m. 现有一船,宽10 m,水面以上高3 m,这条船能否从桥下通过?练习3、点M在圆心为C1的方程:
x2+y2+6x-2y+1=0,点N在圆心为C2的方程x2+y2+2x+4y+1=0,求|MN|的最大值.
作业:
P133习题4.2B组:1,2,3. 30圆系方程1.设圆C1:x2+y2+D1x+E1y+F1=0和圆C2:x2+y2+D2x+E2y+F2=0若两圆相交,则过交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0λ为参数,圆系中部不包括圆C2,当λ= -1时为两圆的公共弦所在直线方程.2.设圆C:x2+y2+Dx+Ey+F=0和直线l:Ax+By+C=0若直线与圆相交,则过交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0(λ为参数)补充θ 如图,设⊙O的圆心在原点,半径是r,与x轴正
半轴的交点为P0,圆上任取一点P,若OP0按逆时
针方向旋转到OP位置所形成的角∠P0OP=θ,
求P点的坐标。圆心为(a,b)、半径为r的圆的参数方程为1.圆的参数方程有什么特点?∴ 当sin(θ )=1时,∵ sin(θ ) [-1,1](2)例. 已知点P(x,y)是圆x2+y2+2x-2 y=0上的一个动点求:(1)x+y的最小值; (2) x2+y2的最大值。
1.圆心和半径能直接求出吗?
2.怎样求出圆的方程?
3.怎样求出支柱A2P2的长度?例4。如图是某圆拱桥的一孔圆拱示意图.该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需要用一个支柱支撑,求支柱A2P2 的长度(精确到0.01m).
练习:某次生产中,一个圆形的零件损坏了,只剩下了如图所示的一部分.现在陈师傅所在的车间准备重新做一个这样的零件,为了获得这个圆形零件的半径,陈师傅在零件上画了一条线段 AB,并作出了 AB 的垂直平分线 MN,而且测得 AB=8 cm,MN=2 cm.根据已有数据,试帮陈师傅求出这个零件的半径.解:以 AB 中点 M 为原点,建立如图所示的平面直角坐标系,由已知有 A(-4,0),B(4,0),N(0,2).
设过 A,B,N 的圆的方程为
x2+y2+Dx+Ey+F=0,
代入 A,B,N 的坐标,可得 解得 因此所求圆的方程为
x2+y2+6y-16=0,
化为标准方程是
x2+(y+3)2=52,
所以这个零件的半径为 5 cm.E例5、已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半.(a,0)(0,b)(c,0)(0,d)证明:过四边形ABCD外接圆的圆心O’ 分别作AC,BD,AD的垂线,垂足分别为
M,N,E,则M,N,E分别是线段AC,BD,AD的中点。由中点坐标公式,得
所以 小结:坐标法解决平面几何问题的“三步曲” 。一、建立适当的平面直角坐标系,用坐标和 方程 表示问题中的几何元素,将平面几何问题转化为代数问题;
二、通过代数运算,解决代数问题;
三、将代数运算结果“翻译” 成几何结论。
这是坐标法解决平面几何问题的“三步曲” ,又简称为“一建二算三译”。 等边三角形ABC中,点D,E分别在边BC,AC上,且有AD,BE相交于点P.求证:解:如下图,建立直角坐标系,使A?B?O三点的坐标分别为
A(4,0)?B(0,3)?O(0,0).解:以B为原点,BC边所在直线为轴,线段 为单位长,建立如图所示的坐标系,则直线AD的方程为直线BE的方程为解以上两方程联立的方程组,得所以点P的坐标是直线PC的斜率因为所以例6:已知△AOB中,|OB|=3,|OA|=4,|AB|=5,点P是△ABO内切圆上一点,求以|PA|?|PB|?|PO|为直径的三个圆面积之和的最大值与最小值.
分析:三个圆面积之和的最值问题实质上是求|PA|2+|PB|2+|PO|2的最值.
由于P是△ABO内切圆上的点,若想找到P点坐标,必须先从△ABO内切圆的方程入手.易求得△ABO的内切点半径r=1,圆心(1,1).
故内切圆的方程是
(x-1)2+(y-1)2=1.
化简为x2+y2-2x-2y+1=0,①
设P(x,y),则
|PA|2+|PB|2+|PO|2
=(x-4)2+y2+x2+(y-3)2+x2+y2
=3x2+3y2-8x-6y+25.②例7.已知实数x,y满足方程x2+y2-4x+1=0,
(1)求 的最值;
(2)求y-x的最值;
(3)求x2+y2的最值.
解:(1)∵圆的标准方程为(x-2)2+y2=3,其圆心为(2,0),半径为 设 即y=kx.
当直线y=kx与圆相切时,斜率k取最大值和最小值.此时
解得k=±
∴ 的最大值为 最小值为 (2)设y-x=b,即y=x+b.当y=x+b与圆相切时,纵截距b取得最大值和最小值,此时
即b=-2± ∴y-x的最大值为 最小值为-2- (3)x2+y2表示圆上一点与原点距离的平方,由平面几何知识可知,它在过原点的连心线与圆的交点处取得最大值和最小值.又圆心到原点的距离为2,
∴x2+y2的最大值为 最小值为拓展提高
练习1、求直线l: 2x-y-2=0被圆C: (x-3)2+y2=0所截得的弦长.2、某圆拱桥的水面跨度20 m,拱高4 m. 现有一船,宽10 m,水面以上高3 m,这条船能否从桥下通过?练习3、点M在圆心为C1的方程:
x2+y2+6x-2y+1=0,点N在圆心为C2的方程x2+y2+2x+4y+1=0,求|MN|的最大值.
作业:
P133习题4.2B组:1,2,3. 30圆系方程1.设圆C1:x2+y2+D1x+E1y+F1=0和圆C2:x2+y2+D2x+E2y+F2=0若两圆相交,则过交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0λ为参数,圆系中部不包括圆C2,当λ= -1时为两圆的公共弦所在直线方程.2.设圆C:x2+y2+Dx+Ey+F=0和直线l:Ax+By+C=0若直线与圆相交,则过交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0(λ为参数)补充θ 如图,设⊙O的圆心在原点,半径是r,与x轴正
半轴的交点为P0,圆上任取一点P,若OP0按逆时
针方向旋转到OP位置所形成的角∠P0OP=θ,
求P点的坐标。圆心为(a,b)、半径为r的圆的参数方程为1.圆的参数方程有什么特点?∴ 当sin(θ )=1时,∵ sin(θ ) [-1,1](2)例. 已知点P(x,y)是圆x2+y2+2x-2 y=0上的一个动点求:(1)x+y的最小值; (2) x2+y2的最大值。
