4.3.1空间直角坐标系
图片预览






文档简介
课件27张PPT。4.3.1空间直角坐标系湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作学习目标:1、空间直角坐标系的建立;
2、空间直角坐标系的划分;
3、空间点的坐标;
4、特殊位置的点的坐标;
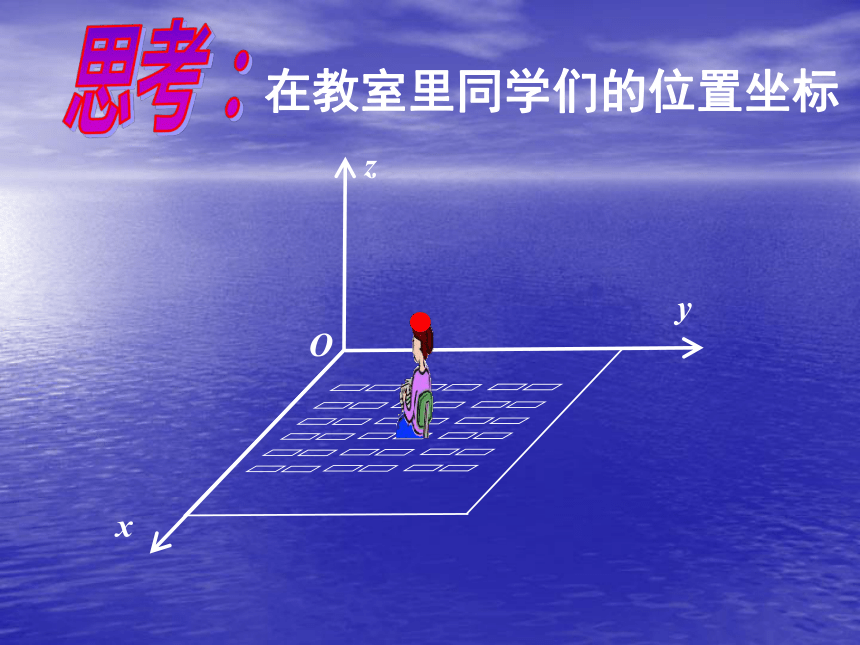
5、空间点的对称问题。问题提出 对于直线上的点,我们可以通过数轴来确定点的位置;对于平面上的点,我们可以通过平面直角坐标系来确定点的位置;对于空间中的点,我们也希望建立适当的坐标系来确定点的位置. 因此,如何在空间中建立坐标系,就成为我们需要研究的课题.那么一点P在直角坐标系中怎么表示呢?OxypABabyOxz思考:在教室里同学们的位置坐标以单位正方体 的
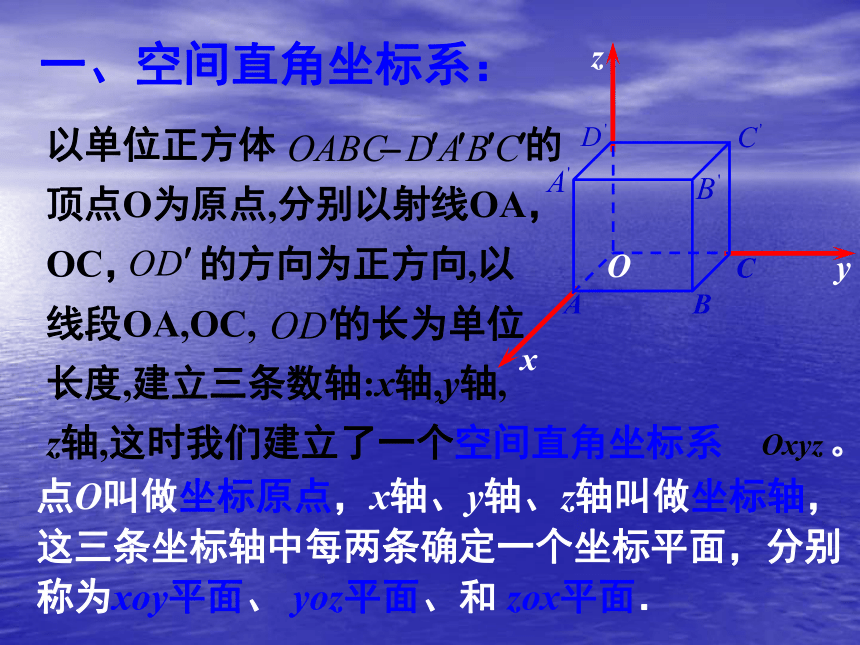
顶点O为原点,分别以射线OA,
OC, 的方向为正方向,以
线段OA,OC, 的长为单位
长度,建立三条数轴:x轴,y轴,
z轴,这时我们建立了一个空间直角坐标系 。一、空间直角坐标系:点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xoy平面、 yoz平面、和 zox平面.右手直角坐标系o1.x轴与y轴、x轴与z轴均成1350,
而z轴垂直于y轴.2.y轴和z轴的单位长度相同,
x轴上的单位长度为y轴
(或z轴)的单位长度的一半.空间直角坐标系的画法:面面面空间直角坐标系共有三个坐标平面、八个卦限。二、空间直角坐标系的划分:思考: 空间直角坐标系中任意一点的位置如何表示?三、空间点的坐标:设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.M’O三、空间点的坐标:设点P、Q和R在x轴、y轴和z轴上的坐标分别是x,y和z,这样空间一点M的坐标可以用有序实数组(x,y,z)来表示, (x,y,z)叫做点M 在此空间直角坐标系中的坐标,记作M(x,y,z).其中x叫做点M的横坐标,
y叫做点M的纵坐标,
z叫做点M的竖坐标.M’O在空间直角坐标系中,作出点A(1,4,4).例解:OP1P1P2P2P小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0。(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)四、特殊位置的点的坐标:xoy平面上的点竖坐标为0yoz平面上的点横坐标为0xoz平面上的点纵坐标为0x轴上的点纵坐标和竖坐标都为0z轴上的点横坐标和纵坐标都为0y轴上的点横坐标和竖坐标都为0(1)坐标平面内的点:(2)坐标轴上的点:规律总结: 例1 如下图,在长方体 中
, 写出四点D’,C,A’,B’的坐标.解: 在z 轴上,且 ,它的竖坐标是2;它的横坐标x与纵坐标y都是零,所以点 的坐标是(0,0,2).
点C 在y 轴上,且 ,它的纵坐标是4;它的横坐标x与竖坐标z 都是零,所以点C的坐标是(0,4,0).
同理,点 的坐标是(3,0,2).典型例题典型例题 解:点B’在平面上的射影是B,因此它的横坐标x与纵坐标y同点B的横坐标x与纵坐标y 相同.在xOy平面上,点B 横坐标x=3,纵坐标y=4;点B’在z轴上的射影是D’,它的竖坐标与点D’的竖坐标相同,点D’的竖坐标z=2.
所以点B’的坐标是(3,4,2). 例1 如下图,在长方体 中
, 写出四点D’,C,A’,B’的坐标.O练习在空间直角坐标系中标出下列各点:
A(0,2,4) B(1,0,5) C(0,2,0) D(1,3,4)134D`D 解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标. 例2 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.典型例题 如图建立空间直角坐标系O-xyz后,试写出全部钠原子所在位置的坐标. 上层的原子所在的平面平行于平面,与轴交点的竖坐标为1,所以,这五个钠原子所在位置的坐标分别是:
(0,0,1),(1,0,1),(1,1,1),(0,1,1),
( , ,1). 中层的原子所在的平面平行于平面,与轴交点的竖坐标为,所以,这四个钠原子所在位置的坐标分别是
( ,0, ),(1, , ),( ,1, ),(0, , );典型例题空间对称点(1)关于原点的对称点是(-x,-y,-z);
(2)关于 x 轴的对称点是(x,-y,-z);
(3)关于 y 轴的对称点是(-x,y,-z);
(4)关于 z 轴的对称点是(-x,-y,z);(5)关于 xOy 坐标平面的对称点是(x,y,-z);
(6)关于 yOz 坐标平面的对称点是(-x,y,z);
(7)关于 zOx 坐标平面的对称点是(x,-y,z).
规律:“关于谁对称则谁不变,其余相反”.五、空间点的对称问题:点M(x,y,z)是空间直角坐标系O-xyz中的一点在空间直角坐标系中,已知点 P(4,3,-5),求点 P关于各坐标轴及坐标平面的对称点.练习【总一总★成竹在胸】1、空间直角坐标系的建立(三步);2、空间直角坐标系的划分(八个卦限);3、空间中点的坐标(一一对应);4、特殊位置的点的坐标(表格);5、空间点的对称问题。课后作业:习题4.3 A组1、2. 1:已知正四棱锥 P-ABCD 的底面边长为 4,侧棱长为
10,试建立适当的空间直角坐标系,写出各顶点的坐标.解:∵正四棱锥 P-ABCD 的底面边长为 4,侧棱长为 10,练一练2、如下图,在长方体OABC-D`A`B`C`中,|OA|=3,|OC|=4,|OD`|=3,A`C`于B`D`相交于点P.分别写出点D` ,B`,P的坐标.P`(0,0,3)(3,4,3)P1(x1,y1,z1),P2(x2,y2,z2),
且线段P1P2的中点为M(x,y,z)则中点坐标公式练一练
高中数学老师欧阳文丰制作学习目标:1、空间直角坐标系的建立;
2、空间直角坐标系的划分;
3、空间点的坐标;
4、特殊位置的点的坐标;
5、空间点的对称问题。问题提出 对于直线上的点,我们可以通过数轴来确定点的位置;对于平面上的点,我们可以通过平面直角坐标系来确定点的位置;对于空间中的点,我们也希望建立适当的坐标系来确定点的位置. 因此,如何在空间中建立坐标系,就成为我们需要研究的课题.那么一点P在直角坐标系中怎么表示呢?OxypABabyOxz思考:在教室里同学们的位置坐标以单位正方体 的
顶点O为原点,分别以射线OA,
OC, 的方向为正方向,以
线段OA,OC, 的长为单位
长度,建立三条数轴:x轴,y轴,
z轴,这时我们建立了一个空间直角坐标系 。一、空间直角坐标系:点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xoy平面、 yoz平面、和 zox平面.右手直角坐标系o1.x轴与y轴、x轴与z轴均成1350,
而z轴垂直于y轴.2.y轴和z轴的单位长度相同,
x轴上的单位长度为y轴
(或z轴)的单位长度的一半.空间直角坐标系的画法:面面面空间直角坐标系共有三个坐标平面、八个卦限。二、空间直角坐标系的划分:思考: 空间直角坐标系中任意一点的位置如何表示?三、空间点的坐标:设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.M’O三、空间点的坐标:设点P、Q和R在x轴、y轴和z轴上的坐标分别是x,y和z,这样空间一点M的坐标可以用有序实数组(x,y,z)来表示, (x,y,z)叫做点M 在此空间直角坐标系中的坐标,记作M(x,y,z).其中x叫做点M的横坐标,
y叫做点M的纵坐标,
z叫做点M的竖坐标.M’O在空间直角坐标系中,作出点A(1,4,4).例解:OP1P1P2P2P小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0。(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)四、特殊位置的点的坐标:xoy平面上的点竖坐标为0yoz平面上的点横坐标为0xoz平面上的点纵坐标为0x轴上的点纵坐标和竖坐标都为0z轴上的点横坐标和纵坐标都为0y轴上的点横坐标和竖坐标都为0(1)坐标平面内的点:(2)坐标轴上的点:规律总结: 例1 如下图,在长方体 中
, 写出四点D’,C,A’,B’的坐标.解: 在z 轴上,且 ,它的竖坐标是2;它的横坐标x与纵坐标y都是零,所以点 的坐标是(0,0,2).
点C 在y 轴上,且 ,它的纵坐标是4;它的横坐标x与竖坐标z 都是零,所以点C的坐标是(0,4,0).
同理,点 的坐标是(3,0,2).典型例题典型例题 解:点B’在平面上的射影是B,因此它的横坐标x与纵坐标y同点B的横坐标x与纵坐标y 相同.在xOy平面上,点B 横坐标x=3,纵坐标y=4;点B’在z轴上的射影是D’,它的竖坐标与点D’的竖坐标相同,点D’的竖坐标z=2.
所以点B’的坐标是(3,4,2). 例1 如下图,在长方体 中
, 写出四点D’,C,A’,B’的坐标.O练习在空间直角坐标系中标出下列各点:
A(0,2,4) B(1,0,5) C(0,2,0) D(1,3,4)134D`D 解:把图中的钠原子分成上、中、下三层来写它们所在位置的坐标. 例2 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为 的小正方体堆积成的正方体),其中色点代表钠原子,黑点代表氯原子.典型例题 如图建立空间直角坐标系O-xyz后,试写出全部钠原子所在位置的坐标. 上层的原子所在的平面平行于平面,与轴交点的竖坐标为1,所以,这五个钠原子所在位置的坐标分别是:
(0,0,1),(1,0,1),(1,1,1),(0,1,1),
( , ,1). 中层的原子所在的平面平行于平面,与轴交点的竖坐标为,所以,这四个钠原子所在位置的坐标分别是
( ,0, ),(1, , ),( ,1, ),(0, , );典型例题空间对称点(1)关于原点的对称点是(-x,-y,-z);
(2)关于 x 轴的对称点是(x,-y,-z);
(3)关于 y 轴的对称点是(-x,y,-z);
(4)关于 z 轴的对称点是(-x,-y,z);(5)关于 xOy 坐标平面的对称点是(x,y,-z);
(6)关于 yOz 坐标平面的对称点是(-x,y,z);
(7)关于 zOx 坐标平面的对称点是(x,-y,z).
规律:“关于谁对称则谁不变,其余相反”.五、空间点的对称问题:点M(x,y,z)是空间直角坐标系O-xyz中的一点在空间直角坐标系中,已知点 P(4,3,-5),求点 P关于各坐标轴及坐标平面的对称点.练习【总一总★成竹在胸】1、空间直角坐标系的建立(三步);2、空间直角坐标系的划分(八个卦限);3、空间中点的坐标(一一对应);4、特殊位置的点的坐标(表格);5、空间点的对称问题。课后作业:习题4.3 A组1、2. 1:已知正四棱锥 P-ABCD 的底面边长为 4,侧棱长为
10,试建立适当的空间直角坐标系,写出各顶点的坐标.解:∵正四棱锥 P-ABCD 的底面边长为 4,侧棱长为 10,练一练2、如下图,在长方体OABC-D`A`B`C`中,|OA|=3,|OC|=4,|OD`|=3,A`C`于B`D`相交于点P.分别写出点D` ,B`,P的坐标.P`(0,0,3)(3,4,3)P1(x1,y1,z1),P2(x2,y2,z2),
且线段P1P2的中点为M(x,y,z)则中点坐标公式练一练
