苏科版八年级数学下册 第9章 中心对称图形---平行四边形 小结与思考教案
文档属性
| 名称 | 苏科版八年级数学下册 第9章 中心对称图形---平行四边形 小结与思考教案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 18:41:27 | ||
图片预览

文档简介
第9章 中心对称图形 小结与思考
一、教材地位分析
本章是在学生小学数学学习中已认识了平行四边形的基础上,从中心对称的角度引导他们对平行四边形认识的进一步深化,本章的学习提高学生演绎推理能力,为后续进一步学好几何打下基础。特殊四边形的性质判定也是中考的考点,因此比较重要。
二、学情分析
执教班级为伯乐中学八年级(1)班,整体学习情况不太乐观,因此希望本节课能帮助学生梳理基础知识点,提高解题能力,激发学习数学的兴趣。
三、教学目标
1.通过归纳梳理平行四边形、矩形、菱形、正方形性质和判定,形成知识体系,厘清知识间的联系与区别,感受图形之间特殊与一般的关系;
2.能有条理、清晰地阐述自己的观点,提高演绎推理的能力.
四、教学重点
归纳梳理平行四边形、矩形、菱形、正方形性质和判定,形成知识体系.
五、教学难点
厘清平行四边形、矩形、菱形、正方形之间的关系,提高演绎推理能力.
六、教学过程
【课堂前测】
1.如图,在□ABCD中,∠D=45°,则∠B=_______°,∠A=________°.
2.如图,在矩形ABCD中,对角线AC、BD相交于点O,等腰三角形有____________________,直角三角形有_______________________.
3.在菱形ABCD中,对角线AC=8,BD=6,则周长是_________,面积是__________.
4.如图,把一张矩形纸片对折两次,然后剪下一个角并打开,剪出的纸片形状一定是_______.
第1题 第2题 第3题 第4题
设计意图:课堂前测有两个目的,一是测试学生基本知识点掌握情况,通过前测可以看出班级学情概况,以便后面环节的开展和应变。二是以填空的形式帮助学生梳理特殊四边形的性质和部分判定。前测相当于本节课的引入,执教者认为引入一定要让学生很容易“够着”,因此题目设计的较简单,这样学生才有继续下去的信心。
第4题较为开放,可以从不同角度思考得出纸片的形状,旨在复习菱形的判定。可以追问:怎样剪,才能得到正方形?由此复习“一个角是直角的菱形是正方形”,教学中可以现场操作演示。
学生活动:独立完成3分钟。
教师活动:巡批,指派学生帮批,关注易错点,总结评价5分钟,形成知识框架。
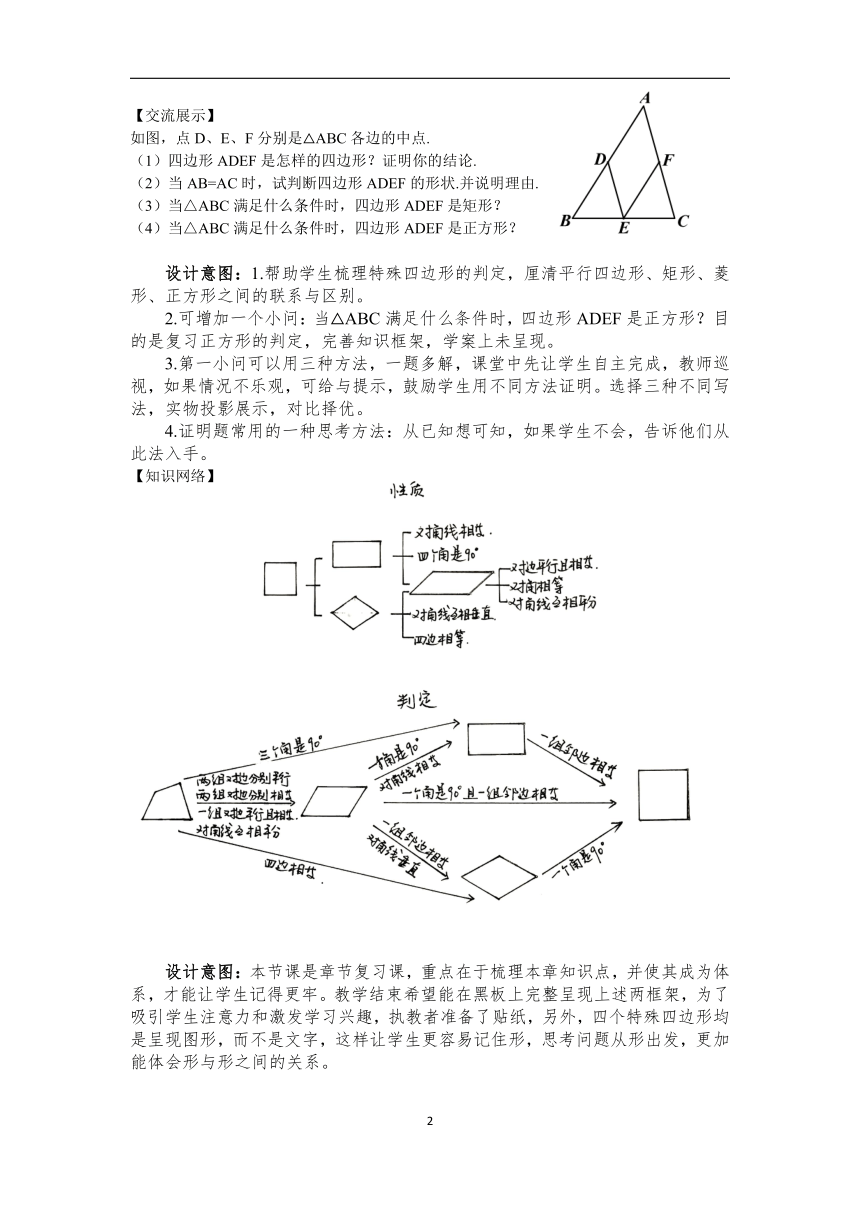
【交流展示】
如图,点D、E、F分别是△ABC各边的中点.
(1)四边形ADEF是怎样的四边形?证明你的结论.
(2)当AB=AC时,试判断四边形ADEF的形状.并说明理由.
(3)当△ABC满足什么条件时,四边形ADEF是矩形?
(4)当△ABC满足什么条件时,四边形ADEF是正方形?
设计意图:1.帮助学生梳理特殊四边形的判定,厘清平行四边形、矩形、菱形、正方形之间的联系与区别。
2.可增加一个小问:当△ABC满足什么条件时,四边形ADEF是正方形?目的是复习正方形的判定,完善知识框架,学案上未呈现。
3.第一小问可以用三种方法,一题多解,课堂中先让学生自主完成,教师巡视,如果情况不乐观,可给与提示,鼓励学生用不同方法证明。选择三种不同写法,实物投影展示,对比择优。
4.证明题常用的一种思考方法:从已知想可知,如果学生不会,告诉他们从此法入手。
【知识网络】
设计意图:本节课是章节复习课,重点在于梳理本章知识点,并使其成为体系,才能让学生记得更牢。教学结束希望能在黑板上完整呈现上述两框架,为了吸引学生注意力和激发学习兴趣,执教者准备了贴纸,另外,四个特殊四边形均是呈现图形,而不是文字,这样让学生更容易记住形,思考问题从形出发,更加能体会形与形之间的关系。
【拓展延伸】
如图,在△ABC中,点O是AC边上的任意一点(不与点A、C重合),过点O作直线MN∥BC, MN交∠BCA的角平分线于点E,交∠DCA的角平分线于点F,
(1)求证:OE=OF.
(2)当点O运动到AC的中点时,试判断四边形AECF的形状.
设计意图:执教者对于本题的取舍比较犹豫,针对执教班级现状,恐怕会比较难推进。
但是1.题目条件较多,充分体现“从已知想可知”的思路,可以借此巩固学生对这一常用思考方法的使用,使其遇到题目会分析,遇到较长的题目不畏惧。
2.此题蕴含了一个基本型,即含有平行线和角平分线的图形中有等腰三角形,这是经常会考到的内容,很有必要培养一下学生从复杂图形中分离出基本图形的能力。
3.这道题还考查了“对角线互相平分的四边形是平行四边形”,“一个角是直角的平行四边形是矩形”,“对角线相等的平行四边形是矩形”等判定,可借助第2问展开讨论,完善框架,也体现了一题多解。
4.此题改编自教材94页第17题,第2问原来是“试确定点O的位置,使四边形AECF是矩形,并加以证明.”,为了降低难度,改成了“当点O运动到AC的中点时,试判断四边形AECF的形状”。但图形仍是点O不在AC中点的样子,目的是让学生不受到图形的干扰,不会轻易地不思考就下结论。
5.教师可设问:题目有哪些条件?由这些条件能得到什么?教师活动:启发,设问,追问,巡批,展示。学生活动:独立思考,讨论,回答,写写写。写出来的才是自己的!
6.如果时间不够,本题pass.
7.其实这题还可以增加一个问:“在第2问的基础上△ABC满足什么条件,四边形AECF是个正方形?”学情较好班级可以增加。
【课堂小结】
1.梳理了平行四边形、矩形、菱形、正方形的性质和判定。
2.学了“从已知想可知”的思考证明题的方法。
3.一个问题可以多种途径到达。
4.还掌握了一个基本图形,平行线和角平分线组合可以得到等腰三角形。
预测学生说不出来,教师引导或者直接总结。
【检测反馈】
1.如图,菱形ABCD中,∠B=60 ,AB=4,则以AC为边长的正方形ACEF的周长为 .
第1题 第2题
2.如图,在△ABC中,点D在BC上,过点D作AB、AC的平行线,分别交AC、AB于点E、F.
(1)四边形AEDF是_______________形;
(2)如果要得到矩形AEDF,那么△ABC应具备什么条件:_____________________;
(3)当AD平分∠BAC时,试判断四边形AFDE的形状.并说明理由。
设计意图:第1题考查的是性质,第2题与例题类似,且蕴含了一个基本图形。执教者认为:本节课讲哪些点,检测反馈就考哪些点,这样能够让普通班级的孩子够得着,树立学习数学的信心,因此检测反馈设计的比较少,不是很难。
2
一、教材地位分析
本章是在学生小学数学学习中已认识了平行四边形的基础上,从中心对称的角度引导他们对平行四边形认识的进一步深化,本章的学习提高学生演绎推理能力,为后续进一步学好几何打下基础。特殊四边形的性质判定也是中考的考点,因此比较重要。
二、学情分析
执教班级为伯乐中学八年级(1)班,整体学习情况不太乐观,因此希望本节课能帮助学生梳理基础知识点,提高解题能力,激发学习数学的兴趣。
三、教学目标
1.通过归纳梳理平行四边形、矩形、菱形、正方形性质和判定,形成知识体系,厘清知识间的联系与区别,感受图形之间特殊与一般的关系;
2.能有条理、清晰地阐述自己的观点,提高演绎推理的能力.
四、教学重点
归纳梳理平行四边形、矩形、菱形、正方形性质和判定,形成知识体系.
五、教学难点
厘清平行四边形、矩形、菱形、正方形之间的关系,提高演绎推理能力.
六、教学过程
【课堂前测】
1.如图,在□ABCD中,∠D=45°,则∠B=_______°,∠A=________°.
2.如图,在矩形ABCD中,对角线AC、BD相交于点O,等腰三角形有____________________,直角三角形有_______________________.
3.在菱形ABCD中,对角线AC=8,BD=6,则周长是_________,面积是__________.
4.如图,把一张矩形纸片对折两次,然后剪下一个角并打开,剪出的纸片形状一定是_______.
第1题 第2题 第3题 第4题
设计意图:课堂前测有两个目的,一是测试学生基本知识点掌握情况,通过前测可以看出班级学情概况,以便后面环节的开展和应变。二是以填空的形式帮助学生梳理特殊四边形的性质和部分判定。前测相当于本节课的引入,执教者认为引入一定要让学生很容易“够着”,因此题目设计的较简单,这样学生才有继续下去的信心。
第4题较为开放,可以从不同角度思考得出纸片的形状,旨在复习菱形的判定。可以追问:怎样剪,才能得到正方形?由此复习“一个角是直角的菱形是正方形”,教学中可以现场操作演示。
学生活动:独立完成3分钟。
教师活动:巡批,指派学生帮批,关注易错点,总结评价5分钟,形成知识框架。
【交流展示】
如图,点D、E、F分别是△ABC各边的中点.
(1)四边形ADEF是怎样的四边形?证明你的结论.
(2)当AB=AC时,试判断四边形ADEF的形状.并说明理由.
(3)当△ABC满足什么条件时,四边形ADEF是矩形?
(4)当△ABC满足什么条件时,四边形ADEF是正方形?
设计意图:1.帮助学生梳理特殊四边形的判定,厘清平行四边形、矩形、菱形、正方形之间的联系与区别。
2.可增加一个小问:当△ABC满足什么条件时,四边形ADEF是正方形?目的是复习正方形的判定,完善知识框架,学案上未呈现。
3.第一小问可以用三种方法,一题多解,课堂中先让学生自主完成,教师巡视,如果情况不乐观,可给与提示,鼓励学生用不同方法证明。选择三种不同写法,实物投影展示,对比择优。
4.证明题常用的一种思考方法:从已知想可知,如果学生不会,告诉他们从此法入手。
【知识网络】
设计意图:本节课是章节复习课,重点在于梳理本章知识点,并使其成为体系,才能让学生记得更牢。教学结束希望能在黑板上完整呈现上述两框架,为了吸引学生注意力和激发学习兴趣,执教者准备了贴纸,另外,四个特殊四边形均是呈现图形,而不是文字,这样让学生更容易记住形,思考问题从形出发,更加能体会形与形之间的关系。
【拓展延伸】
如图,在△ABC中,点O是AC边上的任意一点(不与点A、C重合),过点O作直线MN∥BC, MN交∠BCA的角平分线于点E,交∠DCA的角平分线于点F,
(1)求证:OE=OF.
(2)当点O运动到AC的中点时,试判断四边形AECF的形状.
设计意图:执教者对于本题的取舍比较犹豫,针对执教班级现状,恐怕会比较难推进。
但是1.题目条件较多,充分体现“从已知想可知”的思路,可以借此巩固学生对这一常用思考方法的使用,使其遇到题目会分析,遇到较长的题目不畏惧。
2.此题蕴含了一个基本型,即含有平行线和角平分线的图形中有等腰三角形,这是经常会考到的内容,很有必要培养一下学生从复杂图形中分离出基本图形的能力。
3.这道题还考查了“对角线互相平分的四边形是平行四边形”,“一个角是直角的平行四边形是矩形”,“对角线相等的平行四边形是矩形”等判定,可借助第2问展开讨论,完善框架,也体现了一题多解。
4.此题改编自教材94页第17题,第2问原来是“试确定点O的位置,使四边形AECF是矩形,并加以证明.”,为了降低难度,改成了“当点O运动到AC的中点时,试判断四边形AECF的形状”。但图形仍是点O不在AC中点的样子,目的是让学生不受到图形的干扰,不会轻易地不思考就下结论。
5.教师可设问:题目有哪些条件?由这些条件能得到什么?教师活动:启发,设问,追问,巡批,展示。学生活动:独立思考,讨论,回答,写写写。写出来的才是自己的!
6.如果时间不够,本题pass.
7.其实这题还可以增加一个问:“在第2问的基础上△ABC满足什么条件,四边形AECF是个正方形?”学情较好班级可以增加。
【课堂小结】
1.梳理了平行四边形、矩形、菱形、正方形的性质和判定。
2.学了“从已知想可知”的思考证明题的方法。
3.一个问题可以多种途径到达。
4.还掌握了一个基本图形,平行线和角平分线组合可以得到等腰三角形。
预测学生说不出来,教师引导或者直接总结。
【检测反馈】
1.如图,菱形ABCD中,∠B=60 ,AB=4,则以AC为边长的正方形ACEF的周长为 .
第1题 第2题
2.如图,在△ABC中,点D在BC上,过点D作AB、AC的平行线,分别交AC、AB于点E、F.
(1)四边形AEDF是_______________形;
(2)如果要得到矩形AEDF,那么△ABC应具备什么条件:_____________________;
(3)当AD平分∠BAC时,试判断四边形AFDE的形状.并说明理由。
设计意图:第1题考查的是性质,第2题与例题类似,且蕴含了一个基本图形。执教者认为:本节课讲哪些点,检测反馈就考哪些点,这样能够让普通班级的孩子够得着,树立学习数学的信心,因此检测反馈设计的比较少,不是很难。
2
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
