2021-2022学年湘教版八年级数学下册2.2平行四边形优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学下册2.2平行四边形优生辅导训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 232.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 19:03:09 | ||
图片预览


文档简介
2021-2022学年湘教版八年级数学下册《2-2平行四边形》优生辅导训练(附答案)
一.选择题
1.如图,平行四边形ABCD中,P是四边形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
A.S1+S2=S3+S4 B.S1+S2>S3+S4
C.S1+S3=S2+S4 D.S1+S2<S3+S4
2.如图,在平行四边形ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB的长是( )
A.4 B.2 C.2 D.2
3.如图,在平行四边形ABCD中,点A、B、C的坐标分别为(2,0)、(0,1)、(1,2),则平行四边形ABCD的周长为( )
A. B.6 C.8 D.10
4.如图,在平行四边形ABCD中,点E是BC的中点,作EF⊥AE交CD于F,若∠BAE=45°,AE=4,下列结论:①∠EAF=45°,②AF=AB+CF,③CD=2CF,④S△AEF=8中正确的是( )
A.①②④ B.①③④ C.①②③ D.②③④
5.如图,平行四边形ABCD中,平行于边的两条线段EF,GH把平行四边形ABCD分成四部分,分别记这四部分的面积为S1,S2,S3和S4,则下列等式一定成立的是( )
A.S1=S3 B.S1+S3=S2+S4
C.S3﹣S1=S2﹣S4 D.S1×S3=S2×S4
6.如图,在平行四边形ABCD中,A1、A2、A3、A4和C1、C2、C3、C4分别为AB和CD的五等分点,点B1、B2和D1、D2分别是BC和DA的三等分点,已知四边形ABCD的面积为15,则平行四边形A4B2C4D2(阴影部分)的面积为( )
A.6 B.8 C.9 D.10
二.填空题
7.在 ABCD中,AC,BD相交于点O,若 ABCD的周长为64,且△AOB的周长比△BOC的周长多8,则AB= ,BC= .
8.如图,在平行四边形ABCD中,DB=DC,∠A=65°,CE⊥BD于E,则∠BCE= 度.
9.如图,在 ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2,则AB的长为 .
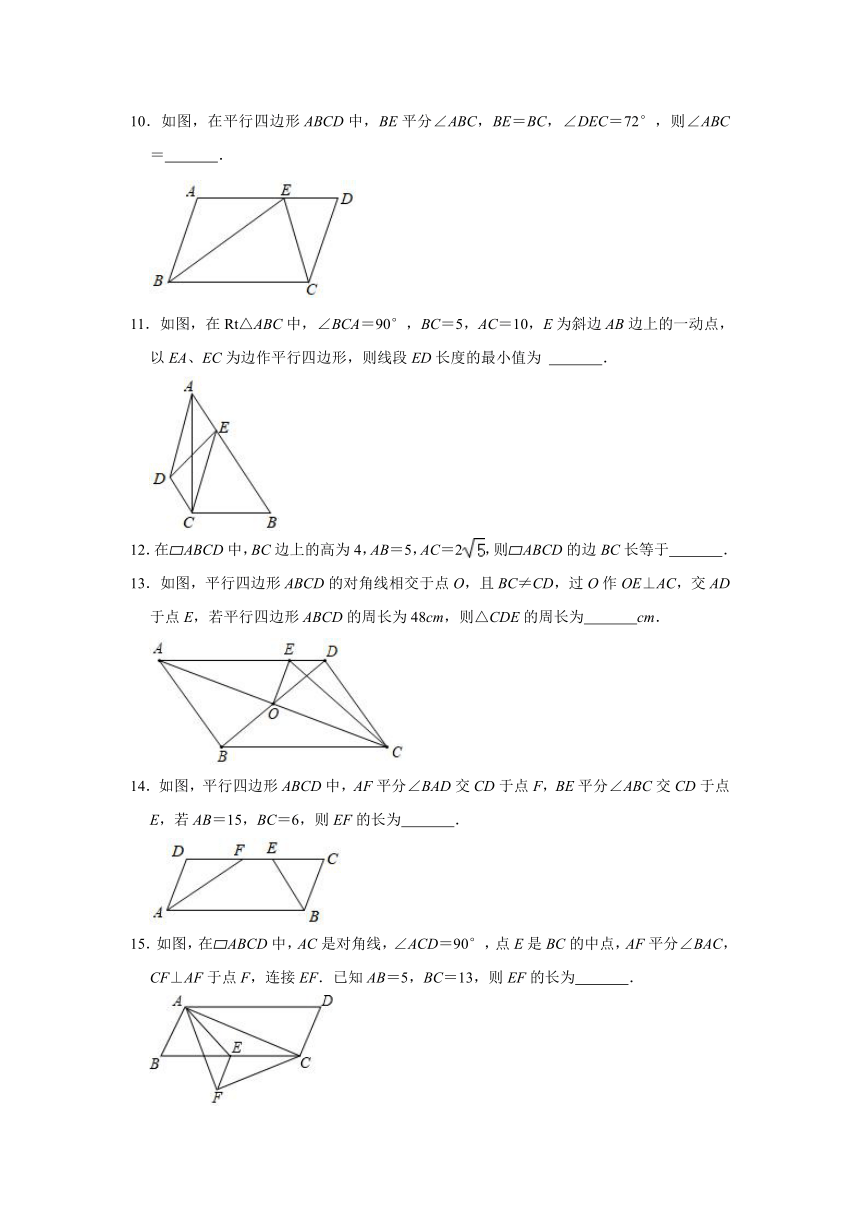
10.如图,在平行四边形ABCD中,BE平分∠ABC,BE=BC,∠DEC=72°,则∠ABC= .
11.如图,在Rt△ABC中,∠BCA=90°,BC=5,AC=10,E为斜边AB边上的一动点,以EA、EC为边作平行四边形,则线段ED长度的最小值为 .
12.在 ABCD中,BC边上的高为4,AB=5,AC=2,则 ABCD的边BC长等于 .
13.如图,平行四边形ABCD的对角线相交于点O,且BC≠CD,过O作OE⊥AC,交AD于点E,若平行四边形ABCD的周长为48cm,则△CDE的周长为 cm.
14.如图,平行四边形ABCD中,AF平分∠BAD交CD于点F,BE平分∠ABC交CD于点E,若AB=15,BC=6,则EF的长为 .
15.如图,在 ABCD中,AC是对角线,∠ACD=90°,点E是BC的中点,AF平分∠BAC,CF⊥AF于点F,连接EF.已知AB=5,BC=13,则EF的长为 .
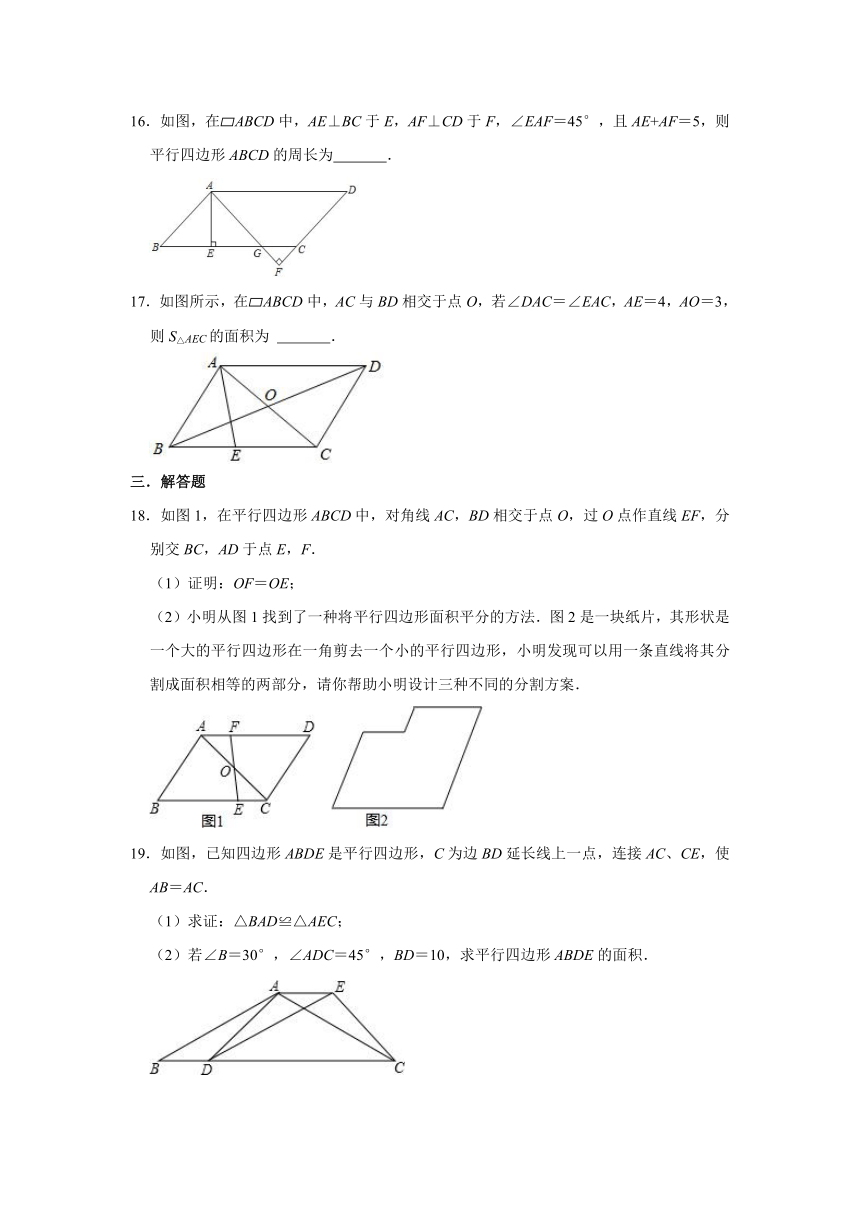
16.如图,在 ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=5,则平行四边形ABCD的周长为 .
17.如图所示,在 ABCD中,AC与BD相交于点O,若∠DAC=∠EAC,AE=4,AO=3,则S△AEC的面积为 .
三.解答题
18.如图1,在平行四边形ABCD中,对角线AC,BD相交于点O,过O点作直线EF,分别交BC,AD于点E,F.
(1)证明:OF=OE;
(2)小明从图1找到了一种将平行四边形面积平分的方法.图2是一块纸片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,小明发现可以用一条直线将其分割成面积相等的两部分,请你帮助小明设计三种不同的分割方案.
19.如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连接AC、CE,使AB=AC.
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
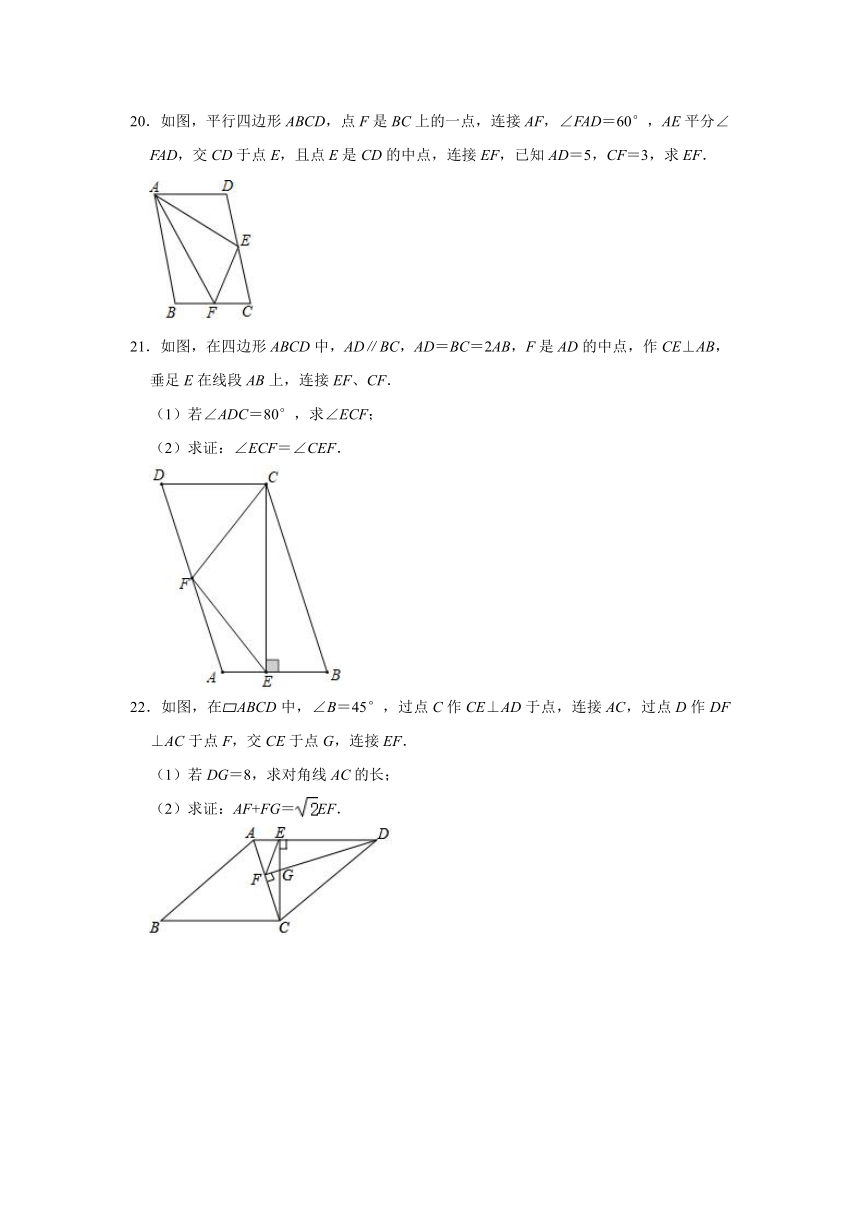
20.如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,求EF.
21.如图,在四边形ABCD中,AD∥BC,AD=BC=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF.
(1)若∠ADC=80°,求∠ECF;
(2)求证:∠ECF=∠CEF.
22.如图,在 ABCD中,∠B=45°,过点C作CE⊥AD于点,连接AC,过点D作DF⊥AC于点F,交CE于点G,连接EF.
(1)若DG=8,求对角线AC的长;
(2)求证:AF+FG=EF.
参考答案与试题解析
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴S1+S3=平行四边形ABCD的面积,
S2+S4=平行四边形ABCD的面积,
∴S1+S3=S2+S4,
故选:C.
2.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴CE=2AB,
∵∠BCD=∠BAD=120°,
∴∠ECF=60°,
∵EF⊥BC,
∴∠CEF=30°,
∴CE=2CF=4,
∴AB=2.
故选:B.
3.解:∵点A、B的坐标分别为(2,0)、(0,1),
∴OA=2,OB=1,
∴AB==,
过C作CE⊥y轴于E,如图所示:
∵点C的坐标为(1,2),
∴CE=1,OE=2,
∴BE=1,
∴BC==,
∴AB+BC=+,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴平行四边形ABCD的周长=2(AB+BC)=2+2
故选:A.
4.解:作EM∥AB交AF于M,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴AB∥EM∥CD,
∴AM:FM=BE:CE,∠AEM=∠BAE=45°,
∵点E是BC的中点,
∴BE=CE,
∴AM=FM,
∴EM是梯形ABCF的中位线,
∴AB+CF=2EM,
∵EF⊥AE,
∴∠AEF=90°,
∴EM=AF=AM=FM,
∴∠EAF=∠AEM=45°,AF=AB+CF,①②正确;
∴△AEF是等腰直角三角形,
∴FE=AE=4,
∴S△AEF=AE×FE=×4×4=8,④正确;
∵∠BAF=∠BAE+∠EAF=90°,
∴AF⊥AB,
∵AB∥CD,
∴AF⊥CD,
当AD=AC时,CF=DF,则CD=2CF,③不正确;
故选:A.
5.解:如根据平行四边形的性质知,S1=AG H2,S4=DH H1=AG H1,S2=GB H2=(DC﹣DH) h2,S3=HC H1=(DC﹣DH) H1,
A、HC及AG,H1、H2的关系不确定,所以S1不一定等于S3,故本选项错误;
B、S1+S3=DC H1﹣DH H1+AG H2,S2+S4=DC h2﹣DH h2+DH H1,∴S1+S3=S2+S4,故本选项错误;
C、S3﹣S1=AG H2﹣HC H1,S2﹣S4=GB H2﹣DH H1,故本选项错误;
D、S1×S3=HC H1 AG H2,S2×S4=GB H2 DH H1,
∵HC=GB,AG=DH,
∴S1×S3=S2×S4,
故本选项正确;
故选:D.
6.解:设AB=5a,BC=3b.AB边上的高是3x,BC边上的高是5y.
∵四边形ABCD的面积为15,
∴5a 3x=3b 5y=15.即ax=by=×15=1.
∵△AA4D2与△B2CC4全等,B2C=BC=b,B2C边上的高是 5y=4y.
则△AA4D2和△B2CC4的面积是2by=2.
同理△D2C4D与△A4BB2的面积是1.
则四边形A4B2C4D2的面积是15﹣2﹣2﹣1﹣1=9.
故选:C.
二.填空题
7.解:∵△AOB的周长比△BOC的周长多8cm,
∴OA+OB+AB﹣OB﹣OC﹣BC=8cm,
∵ABCD是平行四边形,
∴OA=OC,AD=BC,
∴AB﹣BC=8cm,
∵平行四边形ABCD的周长64cm,
∴AB+BC=32cm,
∴AB=20cm,BC=12cm.
故答案为:20,12.
8.解:∵A=65°,
∴∠BCD=65°;
∵DB=DC,
∴∠BCD=∠DBC=65°,
∵CE⊥BD,
∴∠CEB=90°,
∴∠BCE=90°﹣∠DBC=25°.
故答案为:25.
9.解:∵AE为∠DAB的平分线,
∴∠DAE=∠BAE,
∵DC∥AB
∴∠BAE=∠DFA,
∴∠DAE=∠DFA,
∴AD=FD,
又∵F为DC的中点,
∴DF=CF,
∴AD=DF=DC=AB,
∵DG⊥AE,
∴AG=FG,
∵平行四边形ABCD中,
∴AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS),
∴AF=EF=2,
∴AG=,
∴AD==2,
∴AB=2AD=4;
故答案为:4.
10.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DEC=∠ECB=72°,
∵BE=BC,
∴∠BEC=∠BCE=72°,
∴∠EBC=180°﹣∠BCE﹣∠BEC﹣180°﹣72°﹣72°=36°,
∵BE平分∠ABC,
∴∠ABC=2∠EBC=72°,
故答案为:72°.
11.解:如图,过点C作CF⊥AB于F,
在Rt△ABC中,∠BCA=90°,BC=5,AC=10,
∴AB===5,
∵S△ABC=×AC×BC=×AB×CF,
∴CF==2,
∵四边形ADCE是平行四边形,
∴CD∥AB,
∴当DE⊥AB时,DE有最小值,
此时:CF=DE=2,
故答案为2.
12.解:当高在△ABC内部时,如图所示:
在 ABCD中,BC边上的高AE为4,AB=5,AC=2,
∴EC===2,BE===3,
∴BC=CE+BE=2+3=5,
当高在△ABC外部时,如图所示,
同理可得EC=2,BE=3,
∴BC=1,
故答案为:5或1.
13.解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵平行四边形ABCD的周长为48cm,
∴AD+CD=24(cm),
∵OE⊥AC,
∴AE=CE,
∴△CDE的周长为:CD+CE+DE=CD+DE+AE=AD+CD=24(cm).
故答案为:24.
14.解:∵四边形ABCD是平行四边形,
∴∠AFD=∠BAF,
∵AF平分∠ABC,
∴∠DAF=∠BAF,
则∠AFD=∠DAF,
∴AD=FD=6,
同理可证:CE=6,
则EF=CD﹣DF﹣CE=15﹣6﹣6=3.
故答案为:3.
15.解:如图,延长AB、CF交于点H,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC=90°,
∴AC===12,
∵AF平分∠BAC,
∴∠BAF=∠CAF=45°,
在△AFH和△AFC中,
,
∴△AFH≌△AFC(ASA),
∴AC=AH=12,HF=CF,
∴BH=AH﹣AB=7,
∵点E是BC的中点,HF=CF,
∴EF=BH=,
故答案为:.
16.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴∠DAE+∠AEC=180°,
∵∠AEC=90°,∠EAF=45°,
∴∠EAD=90°,∠AGE=45°,
∴∠FAD=45°,
∵AF⊥CD,
∴∠AFD=90°,
∴∠D=45°,
∴△ABE和△AFD都是等腰直角三角形,
∵AE+AF=5,
∴设AE=x,则AF=5﹣x,
∴AB=x,AD=(5﹣x),
∴平行四边形ABCD的周长为:[x+(5﹣x)]×2=10,
故答案为:10.
17.解:连接EO,
∵∠四边形ABCD是平行四边形,
∴∠DAC=∠BCA,AO=CO,
∵∠DAC=∠EAC,
∴∠EAC=∠ECA,
∴AE=CE,
∴EO⊥AC,
∵AE=4,AO=3,
∴OE===,
∴S△AEC=AC OE=×6×=3.
故答案为:3.
三.解答题
18.(1)证明:如图1,∵四边形ABCD是平行四边形,
∴AO=CO,∠FAO=∠ECO,∠AOF=∠COE,
在△AOF和△COE中
,
∴△AOF≌△COE(ASA),
∴OF=OE;
(2)如图2,3,4所示:
19.(1)证明:∵AB=AC,
∴∠B=∠ACB.
又∵四边形ABDE是平行四边形
∴AE∥BD,AE=BD,
∴∠ACB=∠CAE=∠B,
在△DBA和△EAC中
,
∴△DBA≌△EAC(SAS);
(2)解:过A作AG⊥BC,垂足为G.设AG=x,
在Rt△AGD中,∵∠ADC=45°,
∴AG=DG=x,
在Rt△AGB中,∵∠B=30°,
则AB=2x,
∴BG=,
又∵BD=10.
∴BG﹣DG=BD,即,
解得AG=x=,
∴S平行四边形ABDE=BD AG=10×()=.
20.解:如图,延长AE,BC交于点G,
∵点E是CD的中点,
∴DE=CE,
∵平行四边形ABCD中,AD∥BC,
∴∠D=∠ECG,
又∵∠AED=∠GEC,
∴△ADE≌△GCE,
∴CG=AD=5,AE=GE,
又∵AE平分∠FAD,AD∥BC,
∴∠FAE=∠DAE=∠G=∠DAF=30°,
∴AF=GF=3+5=8,
又∵E是AG的中点,
∴FE⊥AG,
∴Rt△AEF中,EF=AF=4,
故答案为:4.
21.解:(1)∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵F是AD的中点,
∴AF=FD,
∵在 ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF=(180°﹣80°)=50°,
∵CE⊥AB,
∴CE⊥CD,
∴∠DCE=90°,
∴∠ECF=90°﹣50°=40°;
(2)如图,延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=EM=FE,
∴∠ECF=∠CEF.
22.解:(1)∵在 ABCD中,∠B=45°,
∴∠ADC=∠B=45°,
∵CE⊥AD,
∴△CDE是等腰直角三角形,
∴CE=DE,∠DEC=∠AEC=90°,
∵DF⊥AC,
∴∠CFD=∠DEC=90°,
∴∠DGE=∠CGF,
∴∠EDG=∠ECA,
∴△DEG≌△CEA(ASA),
∴AC=DG=8;
(2)过E作EH⊥EF交DF于H,
∵∠FEH=∠DEC=90°,
∴∠DEH=∠CEF,
∵∠EDH=∠ECF,DE=CE,
∴△DEH≌△CEF(ASA),
∴EF=EH,DH=CF,
∴AC﹣CF=DG﹣DH,
即AF=HG,
∵FH=FG+GH=EF,
∴AF+FG=EF.
一.选择题
1.如图,平行四边形ABCD中,P是四边形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
A.S1+S2=S3+S4 B.S1+S2>S3+S4
C.S1+S3=S2+S4 D.S1+S2<S3+S4
2.如图,在平行四边形ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB的长是( )
A.4 B.2 C.2 D.2
3.如图,在平行四边形ABCD中,点A、B、C的坐标分别为(2,0)、(0,1)、(1,2),则平行四边形ABCD的周长为( )
A. B.6 C.8 D.10
4.如图,在平行四边形ABCD中,点E是BC的中点,作EF⊥AE交CD于F,若∠BAE=45°,AE=4,下列结论:①∠EAF=45°,②AF=AB+CF,③CD=2CF,④S△AEF=8中正确的是( )
A.①②④ B.①③④ C.①②③ D.②③④
5.如图,平行四边形ABCD中,平行于边的两条线段EF,GH把平行四边形ABCD分成四部分,分别记这四部分的面积为S1,S2,S3和S4,则下列等式一定成立的是( )
A.S1=S3 B.S1+S3=S2+S4
C.S3﹣S1=S2﹣S4 D.S1×S3=S2×S4
6.如图,在平行四边形ABCD中,A1、A2、A3、A4和C1、C2、C3、C4分别为AB和CD的五等分点,点B1、B2和D1、D2分别是BC和DA的三等分点,已知四边形ABCD的面积为15,则平行四边形A4B2C4D2(阴影部分)的面积为( )
A.6 B.8 C.9 D.10
二.填空题
7.在 ABCD中,AC,BD相交于点O,若 ABCD的周长为64,且△AOB的周长比△BOC的周长多8,则AB= ,BC= .
8.如图,在平行四边形ABCD中,DB=DC,∠A=65°,CE⊥BD于E,则∠BCE= 度.
9.如图,在 ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2,则AB的长为 .
10.如图,在平行四边形ABCD中,BE平分∠ABC,BE=BC,∠DEC=72°,则∠ABC= .
11.如图,在Rt△ABC中,∠BCA=90°,BC=5,AC=10,E为斜边AB边上的一动点,以EA、EC为边作平行四边形,则线段ED长度的最小值为 .
12.在 ABCD中,BC边上的高为4,AB=5,AC=2,则 ABCD的边BC长等于 .
13.如图,平行四边形ABCD的对角线相交于点O,且BC≠CD,过O作OE⊥AC,交AD于点E,若平行四边形ABCD的周长为48cm,则△CDE的周长为 cm.
14.如图,平行四边形ABCD中,AF平分∠BAD交CD于点F,BE平分∠ABC交CD于点E,若AB=15,BC=6,则EF的长为 .
15.如图,在 ABCD中,AC是对角线,∠ACD=90°,点E是BC的中点,AF平分∠BAC,CF⊥AF于点F,连接EF.已知AB=5,BC=13,则EF的长为 .
16.如图,在 ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=5,则平行四边形ABCD的周长为 .
17.如图所示,在 ABCD中,AC与BD相交于点O,若∠DAC=∠EAC,AE=4,AO=3,则S△AEC的面积为 .
三.解答题
18.如图1,在平行四边形ABCD中,对角线AC,BD相交于点O,过O点作直线EF,分别交BC,AD于点E,F.
(1)证明:OF=OE;
(2)小明从图1找到了一种将平行四边形面积平分的方法.图2是一块纸片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,小明发现可以用一条直线将其分割成面积相等的两部分,请你帮助小明设计三种不同的分割方案.
19.如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连接AC、CE,使AB=AC.
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
20.如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,求EF.
21.如图,在四边形ABCD中,AD∥BC,AD=BC=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF.
(1)若∠ADC=80°,求∠ECF;
(2)求证:∠ECF=∠CEF.
22.如图,在 ABCD中,∠B=45°,过点C作CE⊥AD于点,连接AC,过点D作DF⊥AC于点F,交CE于点G,连接EF.
(1)若DG=8,求对角线AC的长;
(2)求证:AF+FG=EF.
参考答案与试题解析
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴S1+S3=平行四边形ABCD的面积,
S2+S4=平行四边形ABCD的面积,
∴S1+S3=S2+S4,
故选:C.
2.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴CE=2AB,
∵∠BCD=∠BAD=120°,
∴∠ECF=60°,
∵EF⊥BC,
∴∠CEF=30°,
∴CE=2CF=4,
∴AB=2.
故选:B.
3.解:∵点A、B的坐标分别为(2,0)、(0,1),
∴OA=2,OB=1,
∴AB==,
过C作CE⊥y轴于E,如图所示:
∵点C的坐标为(1,2),
∴CE=1,OE=2,
∴BE=1,
∴BC==,
∴AB+BC=+,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴平行四边形ABCD的周长=2(AB+BC)=2+2
故选:A.
4.解:作EM∥AB交AF于M,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴AB∥EM∥CD,
∴AM:FM=BE:CE,∠AEM=∠BAE=45°,
∵点E是BC的中点,
∴BE=CE,
∴AM=FM,
∴EM是梯形ABCF的中位线,
∴AB+CF=2EM,
∵EF⊥AE,
∴∠AEF=90°,
∴EM=AF=AM=FM,
∴∠EAF=∠AEM=45°,AF=AB+CF,①②正确;
∴△AEF是等腰直角三角形,
∴FE=AE=4,
∴S△AEF=AE×FE=×4×4=8,④正确;
∵∠BAF=∠BAE+∠EAF=90°,
∴AF⊥AB,
∵AB∥CD,
∴AF⊥CD,
当AD=AC时,CF=DF,则CD=2CF,③不正确;
故选:A.
5.解:如根据平行四边形的性质知,S1=AG H2,S4=DH H1=AG H1,S2=GB H2=(DC﹣DH) h2,S3=HC H1=(DC﹣DH) H1,
A、HC及AG,H1、H2的关系不确定,所以S1不一定等于S3,故本选项错误;
B、S1+S3=DC H1﹣DH H1+AG H2,S2+S4=DC h2﹣DH h2+DH H1,∴S1+S3=S2+S4,故本选项错误;
C、S3﹣S1=AG H2﹣HC H1,S2﹣S4=GB H2﹣DH H1,故本选项错误;
D、S1×S3=HC H1 AG H2,S2×S4=GB H2 DH H1,
∵HC=GB,AG=DH,
∴S1×S3=S2×S4,
故本选项正确;
故选:D.
6.解:设AB=5a,BC=3b.AB边上的高是3x,BC边上的高是5y.
∵四边形ABCD的面积为15,
∴5a 3x=3b 5y=15.即ax=by=×15=1.
∵△AA4D2与△B2CC4全等,B2C=BC=b,B2C边上的高是 5y=4y.
则△AA4D2和△B2CC4的面积是2by=2.
同理△D2C4D与△A4BB2的面积是1.
则四边形A4B2C4D2的面积是15﹣2﹣2﹣1﹣1=9.
故选:C.
二.填空题
7.解:∵△AOB的周长比△BOC的周长多8cm,
∴OA+OB+AB﹣OB﹣OC﹣BC=8cm,
∵ABCD是平行四边形,
∴OA=OC,AD=BC,
∴AB﹣BC=8cm,
∵平行四边形ABCD的周长64cm,
∴AB+BC=32cm,
∴AB=20cm,BC=12cm.
故答案为:20,12.
8.解:∵A=65°,
∴∠BCD=65°;
∵DB=DC,
∴∠BCD=∠DBC=65°,
∵CE⊥BD,
∴∠CEB=90°,
∴∠BCE=90°﹣∠DBC=25°.
故答案为:25.
9.解:∵AE为∠DAB的平分线,
∴∠DAE=∠BAE,
∵DC∥AB
∴∠BAE=∠DFA,
∴∠DAE=∠DFA,
∴AD=FD,
又∵F为DC的中点,
∴DF=CF,
∴AD=DF=DC=AB,
∵DG⊥AE,
∴AG=FG,
∵平行四边形ABCD中,
∴AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS),
∴AF=EF=2,
∴AG=,
∴AD==2,
∴AB=2AD=4;
故答案为:4.
10.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DEC=∠ECB=72°,
∵BE=BC,
∴∠BEC=∠BCE=72°,
∴∠EBC=180°﹣∠BCE﹣∠BEC﹣180°﹣72°﹣72°=36°,
∵BE平分∠ABC,
∴∠ABC=2∠EBC=72°,
故答案为:72°.
11.解:如图,过点C作CF⊥AB于F,
在Rt△ABC中,∠BCA=90°,BC=5,AC=10,
∴AB===5,
∵S△ABC=×AC×BC=×AB×CF,
∴CF==2,
∵四边形ADCE是平行四边形,
∴CD∥AB,
∴当DE⊥AB时,DE有最小值,
此时:CF=DE=2,
故答案为2.
12.解:当高在△ABC内部时,如图所示:
在 ABCD中,BC边上的高AE为4,AB=5,AC=2,
∴EC===2,BE===3,
∴BC=CE+BE=2+3=5,
当高在△ABC外部时,如图所示,
同理可得EC=2,BE=3,
∴BC=1,
故答案为:5或1.
13.解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵平行四边形ABCD的周长为48cm,
∴AD+CD=24(cm),
∵OE⊥AC,
∴AE=CE,
∴△CDE的周长为:CD+CE+DE=CD+DE+AE=AD+CD=24(cm).
故答案为:24.
14.解:∵四边形ABCD是平行四边形,
∴∠AFD=∠BAF,
∵AF平分∠ABC,
∴∠DAF=∠BAF,
则∠AFD=∠DAF,
∴AD=FD=6,
同理可证:CE=6,
则EF=CD﹣DF﹣CE=15﹣6﹣6=3.
故答案为:3.
15.解:如图,延长AB、CF交于点H,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC=90°,
∴AC===12,
∵AF平分∠BAC,
∴∠BAF=∠CAF=45°,
在△AFH和△AFC中,
,
∴△AFH≌△AFC(ASA),
∴AC=AH=12,HF=CF,
∴BH=AH﹣AB=7,
∵点E是BC的中点,HF=CF,
∴EF=BH=,
故答案为:.
16.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴∠DAE+∠AEC=180°,
∵∠AEC=90°,∠EAF=45°,
∴∠EAD=90°,∠AGE=45°,
∴∠FAD=45°,
∵AF⊥CD,
∴∠AFD=90°,
∴∠D=45°,
∴△ABE和△AFD都是等腰直角三角形,
∵AE+AF=5,
∴设AE=x,则AF=5﹣x,
∴AB=x,AD=(5﹣x),
∴平行四边形ABCD的周长为:[x+(5﹣x)]×2=10,
故答案为:10.
17.解:连接EO,
∵∠四边形ABCD是平行四边形,
∴∠DAC=∠BCA,AO=CO,
∵∠DAC=∠EAC,
∴∠EAC=∠ECA,
∴AE=CE,
∴EO⊥AC,
∵AE=4,AO=3,
∴OE===,
∴S△AEC=AC OE=×6×=3.
故答案为:3.
三.解答题
18.(1)证明:如图1,∵四边形ABCD是平行四边形,
∴AO=CO,∠FAO=∠ECO,∠AOF=∠COE,
在△AOF和△COE中
,
∴△AOF≌△COE(ASA),
∴OF=OE;
(2)如图2,3,4所示:
19.(1)证明:∵AB=AC,
∴∠B=∠ACB.
又∵四边形ABDE是平行四边形
∴AE∥BD,AE=BD,
∴∠ACB=∠CAE=∠B,
在△DBA和△EAC中
,
∴△DBA≌△EAC(SAS);
(2)解:过A作AG⊥BC,垂足为G.设AG=x,
在Rt△AGD中,∵∠ADC=45°,
∴AG=DG=x,
在Rt△AGB中,∵∠B=30°,
则AB=2x,
∴BG=,
又∵BD=10.
∴BG﹣DG=BD,即,
解得AG=x=,
∴S平行四边形ABDE=BD AG=10×()=.
20.解:如图,延长AE,BC交于点G,
∵点E是CD的中点,
∴DE=CE,
∵平行四边形ABCD中,AD∥BC,
∴∠D=∠ECG,
又∵∠AED=∠GEC,
∴△ADE≌△GCE,
∴CG=AD=5,AE=GE,
又∵AE平分∠FAD,AD∥BC,
∴∠FAE=∠DAE=∠G=∠DAF=30°,
∴AF=GF=3+5=8,
又∵E是AG的中点,
∴FE⊥AG,
∴Rt△AEF中,EF=AF=4,
故答案为:4.
21.解:(1)∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵F是AD的中点,
∴AF=FD,
∵在 ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF=(180°﹣80°)=50°,
∵CE⊥AB,
∴CE⊥CD,
∴∠DCE=90°,
∴∠ECF=90°﹣50°=40°;
(2)如图,延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=EM=FE,
∴∠ECF=∠CEF.
22.解:(1)∵在 ABCD中,∠B=45°,
∴∠ADC=∠B=45°,
∵CE⊥AD,
∴△CDE是等腰直角三角形,
∴CE=DE,∠DEC=∠AEC=90°,
∵DF⊥AC,
∴∠CFD=∠DEC=90°,
∴∠DGE=∠CGF,
∴∠EDG=∠ECA,
∴△DEG≌△CEA(ASA),
∴AC=DG=8;
(2)过E作EH⊥EF交DF于H,
∵∠FEH=∠DEC=90°,
∴∠DEH=∠CEF,
∵∠EDH=∠ECF,DE=CE,
∴△DEH≌△CEF(ASA),
∴EF=EH,DH=CF,
∴AC﹣CF=DG﹣DH,
即AF=HG,
∵FH=FG+GH=EF,
∴AF+FG=EF.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
