北师大版七年级数学下册 2.3 平行线的性质 课件(共30张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 2.3 平行线的性质 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 10:34:31 | ||
图片预览





文档简介
(共30张PPT)
北师大版七年级下册数学
平行线的性质
第二章 相交线与平行线
01
03
02
探索、归纳平行线的性质(重点)
学习目标
会用平行线的性质进行简单的计算与说理(难点)
了解平行线的性质和判定的区别
思考回顾
平行线的判定
由“角”的数量关系(相等或互补)定“线”位置关系(平行)
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
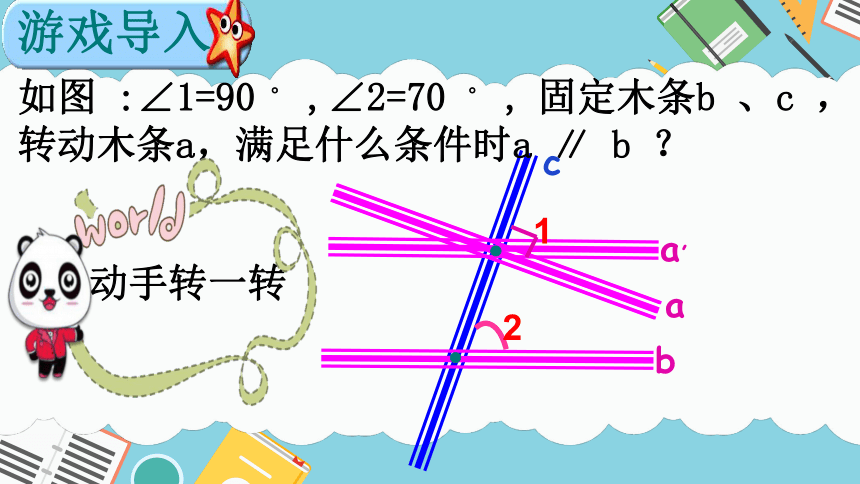
如图 :∠1=90 。 ,∠2=70 。 , 固定木条b 、c ,转动木条a,满足什么条件时a ∥ b ?
2
1
a
b
c
a,
游戏导入
动手转一转
两
直
线
平
行
角的
关系
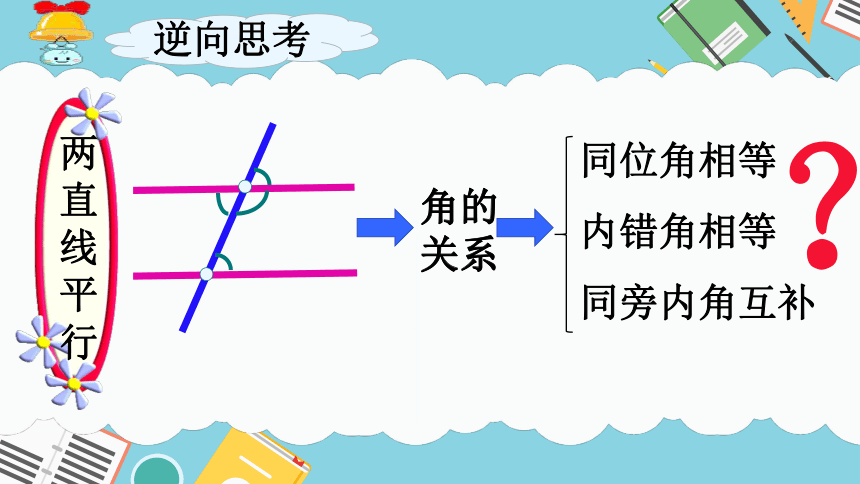
逆向思考
?
同位角相等
内错角相等
同旁内角互补
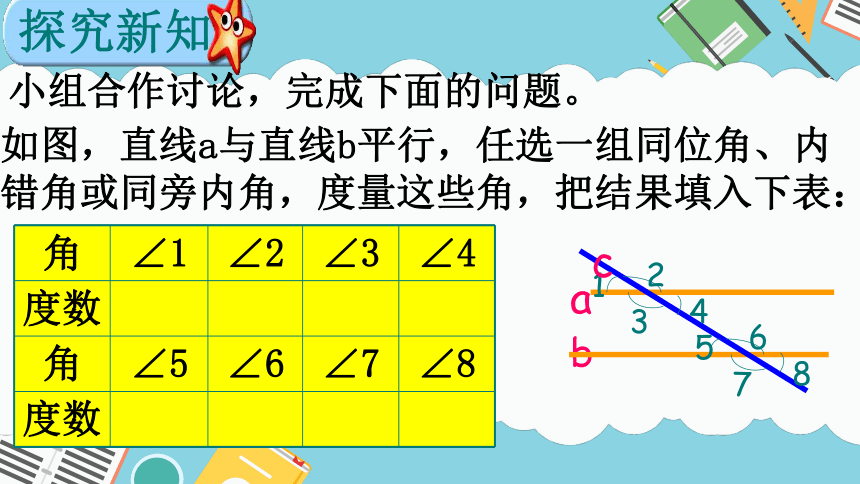
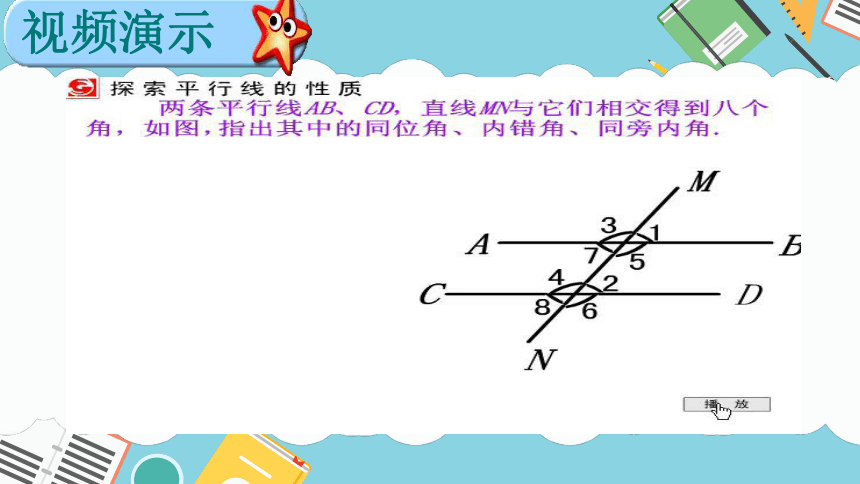
如图,直线a与直线b平行,任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
小组合作讨论,完成下面的问题。
b
1
2
3
4
5
6
7
8
a
c
探究新知
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
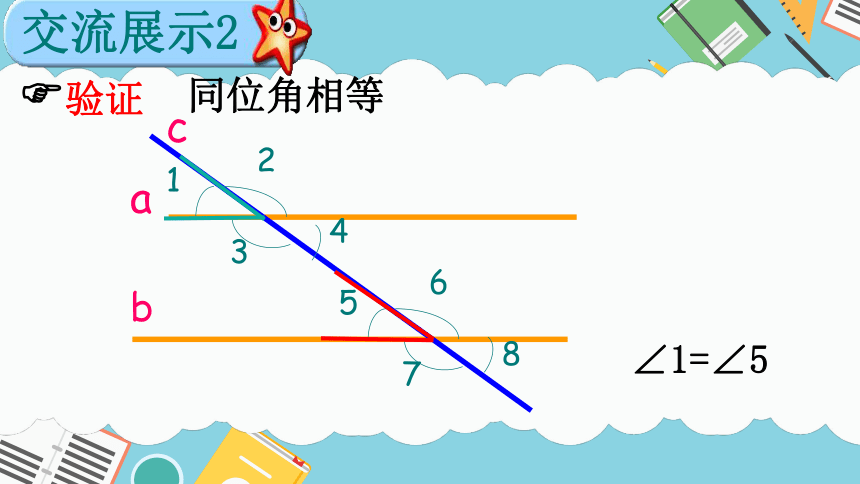
交流展示1
观察
各对同位角、内错角、同旁内角的度数之间
有什么关系?说出你的猜想
相等
相等
互补
猜想
两条平行线被第三条直线所截,同位角__,内错角__ ,同旁内角__.
b
1
2
3
4
5
6
7
8
a
c
∠1=∠5
验证
同位角相等
交流展示2
b
1
2
3
4
5
6
7
8
a
c
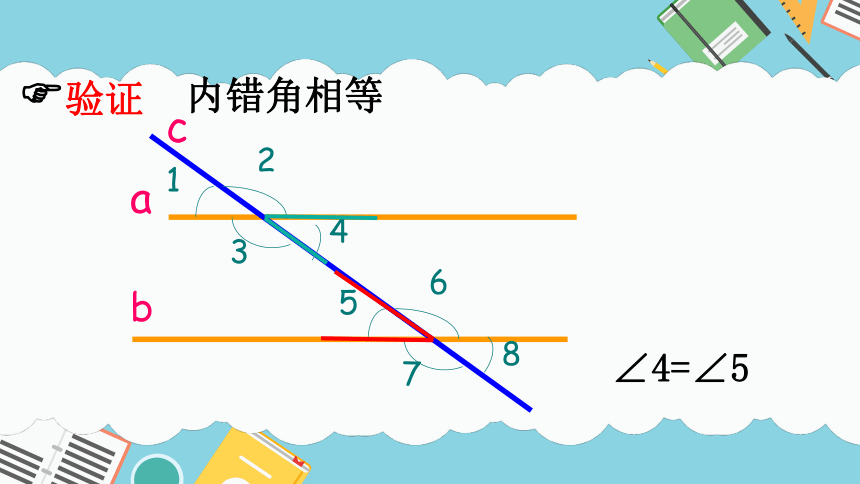
∠4=∠5
验证
内错角相等
b
1
2
3
4
5
6
7
8
a
c
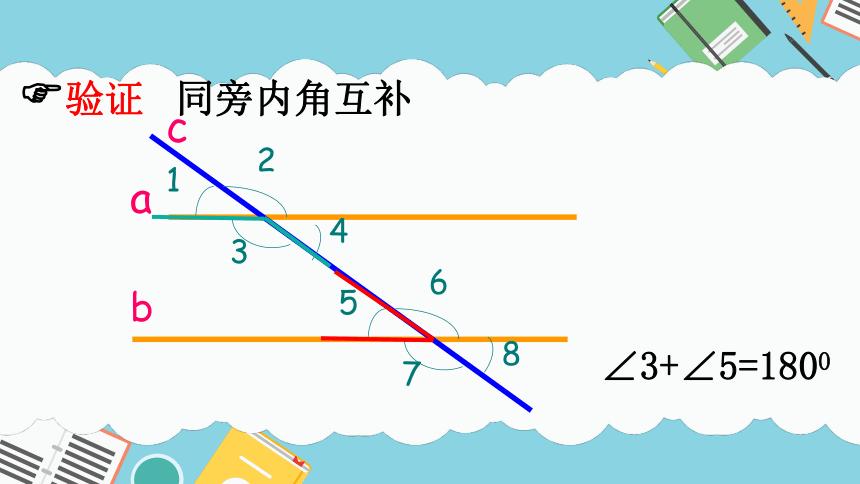
∠3+∠5=1800
同旁内角互补
验证
视频演示
思考突破
再换一组平行线,同样度量并计算各个角的度数,你的猜想还成立吗?
平行线的性质1
两条平行线被第三条直线所截,同位角相等。
b
a
c
1
2
回顾总结
几何语言:
∵a∥b,
∴∠1=∠2.(两直线平行,同位角相等)
平行线的性质2
两条平行线被第三条直线所截,内错角相等。
几何语言:
∵a∥b,
∴∠2=∠3.(两直线平行,内错角相等)
b
2
a
3
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
几何语言:
∵a∥b,
∴∠4+∠2=1800.(两直线平行,同旁内角互补)
c
b
2
a
4
例题:如图,一束平行光线 AB 与DE 射向一个水平镜面后被反射,此时 ∠1 =∠2,∠3 =∠4.
(1)∠1 与∠3的大小有什么关系?
∠2与∠4 呢?
(2)反射光线BC与EF也平行吗?
直击例题
请选择一个你能完成的任务,并预祝你能出色的完成任务:
超人版
智慧版
3幻灯片 19
1幻灯片 18
2幻灯片 19
3幻灯片 23
1幻灯片 21
2幻灯片 22
是“玩家”就玩出水平
知识检测
NEXT
C
智慧版
1、如图,直线a ∥b,直线c与a,b相交,∠1=70°,则∠2=( )。
A.20 ° B.50 ° C.70 ° D.110 °
3
BACK
智慧版
2、如图:AB,CD被EF所截,AB∥CD(填空)。
若∠1=120o,则∠2=
( )
∠3=180-∠1=
( )
A
B
C
D
E
F
1
2
3
600
两直线平行,内错角相等
1200
两直线平行,同旁内角互补
BACK
智慧版
BACK
3、如图,将一块直角三角板的直角顶点放在直尺的一边上,如果∠1= 50 °,那么∠2的度数是 。
40 °
50°
3
超人版
BACK
1、如图,已知∠B=∠C,AE∥BC,试说明AE平分∠CAD。
BACK
2、如图,∠1=∠2,∠D=50°,求∠B的度数。
超人版
BACK
超人版
B
A
2
1
D
C
E
4
3
3、如图,平行线AB、CD被直线AE所截.
(1)从∠1=1100 可以知道∠2
是多少度 为什么
(2)从∠1=1100 可以知道∠3
是多少度 为什么
(3)从∠1=1100可以知道∠4
是多少度 为什么
条件
判定
结论
条件
性质
结论
同位角相等
内错角相等
同旁内角互补
两
直
线
平
行
两
直
线
平
行
同位角相等
内错角相等
同旁内角互补
两条平行线被第三条直线直线所截
对比强化
A
B
o
P
Q
R
1:如图:∠AOB的边OA为平面镜,一束光线PQ平行于OB边射到OA上,反射光线QR交OB于R
1.若∠PQR=50 0则 ∠AOB=( )
650
50。
2.若反射光线QR与OB 垂直,光线沿原路返回,则∠AOB=( )
450
R
A
B
P
Q
O
提升自我
2、
(1)如图1,AB∥CD,试说明∠B+∠D=∠BED.
(2)如图2,AB∥CD,试说明:∠B+∠BED+∠D=360°.
图1
图2
F
1
2
F
1
2
激发潜能
拓广探究
两条平行直线被第三条直线所截,一对同位角的角平分线有何位置关系?内错角的角平分线、同旁内角的角平分线它们分别又有何位置关系呢?
线的关系
角的关系
判定
性质
课堂小结
位置
数量
合情推理 逆向思维
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的性质
平行线的判定
作业布置
基础题:课本51页随堂练习1题,习题2.5的1,2题
提高题:推广探究题
谢谢观赏
北师大版七年级下册数学
平行线的性质
第二章 相交线与平行线
01
03
02
探索、归纳平行线的性质(重点)
学习目标
会用平行线的性质进行简单的计算与说理(难点)
了解平行线的性质和判定的区别
思考回顾
平行线的判定
由“角”的数量关系(相等或互补)定“线”位置关系(平行)
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
如图 :∠1=90 。 ,∠2=70 。 , 固定木条b 、c ,转动木条a,满足什么条件时a ∥ b ?
2
1
a
b
c
a,
游戏导入
动手转一转
两
直
线
平
行
角的
关系
逆向思考
?
同位角相等
内错角相等
同旁内角互补
如图,直线a与直线b平行,任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
小组合作讨论,完成下面的问题。
b
1
2
3
4
5
6
7
8
a
c
探究新知
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
交流展示1
观察
各对同位角、内错角、同旁内角的度数之间
有什么关系?说出你的猜想
相等
相等
互补
猜想
两条平行线被第三条直线所截,同位角__,内错角__ ,同旁内角__.
b
1
2
3
4
5
6
7
8
a
c
∠1=∠5
验证
同位角相等
交流展示2
b
1
2
3
4
5
6
7
8
a
c
∠4=∠5
验证
内错角相等
b
1
2
3
4
5
6
7
8
a
c
∠3+∠5=1800
同旁内角互补
验证
视频演示
思考突破
再换一组平行线,同样度量并计算各个角的度数,你的猜想还成立吗?
平行线的性质1
两条平行线被第三条直线所截,同位角相等。
b
a
c
1
2
回顾总结
几何语言:
∵a∥b,
∴∠1=∠2.(两直线平行,同位角相等)
平行线的性质2
两条平行线被第三条直线所截,内错角相等。
几何语言:
∵a∥b,
∴∠2=∠3.(两直线平行,内错角相等)
b
2
a
3
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
几何语言:
∵a∥b,
∴∠4+∠2=1800.(两直线平行,同旁内角互补)
c
b
2
a
4
例题:如图,一束平行光线 AB 与DE 射向一个水平镜面后被反射,此时 ∠1 =∠2,∠3 =∠4.
(1)∠1 与∠3的大小有什么关系?
∠2与∠4 呢?
(2)反射光线BC与EF也平行吗?
直击例题
请选择一个你能完成的任务,并预祝你能出色的完成任务:
超人版
智慧版
3幻灯片 19
1幻灯片 18
2幻灯片 19
3幻灯片 23
1幻灯片 21
2幻灯片 22
是“玩家”就玩出水平
知识检测
NEXT
C
智慧版
1、如图,直线a ∥b,直线c与a,b相交,∠1=70°,则∠2=( )。
A.20 ° B.50 ° C.70 ° D.110 °
3
BACK
智慧版
2、如图:AB,CD被EF所截,AB∥CD(填空)。
若∠1=120o,则∠2=
( )
∠3=180-∠1=
( )
A
B
C
D
E
F
1
2
3
600
两直线平行,内错角相等
1200
两直线平行,同旁内角互补
BACK
智慧版
BACK
3、如图,将一块直角三角板的直角顶点放在直尺的一边上,如果∠1= 50 °,那么∠2的度数是 。
40 °
50°
3
超人版
BACK
1、如图,已知∠B=∠C,AE∥BC,试说明AE平分∠CAD。
BACK
2、如图,∠1=∠2,∠D=50°,求∠B的度数。
超人版
BACK
超人版
B
A
2
1
D
C
E
4
3
3、如图,平行线AB、CD被直线AE所截.
(1)从∠1=1100 可以知道∠2
是多少度 为什么
(2)从∠1=1100 可以知道∠3
是多少度 为什么
(3)从∠1=1100可以知道∠4
是多少度 为什么
条件
判定
结论
条件
性质
结论
同位角相等
内错角相等
同旁内角互补
两
直
线
平
行
两
直
线
平
行
同位角相等
内错角相等
同旁内角互补
两条平行线被第三条直线直线所截
对比强化
A
B
o
P
Q
R
1:如图:∠AOB的边OA为平面镜,一束光线PQ平行于OB边射到OA上,反射光线QR交OB于R
1.若∠PQR=50 0则 ∠AOB=( )
650
50。
2.若反射光线QR与OB 垂直,光线沿原路返回,则∠AOB=( )
450
R
A
B
P
Q
O
提升自我
2、
(1)如图1,AB∥CD,试说明∠B+∠D=∠BED.
(2)如图2,AB∥CD,试说明:∠B+∠BED+∠D=360°.
图1
图2
F
1
2
F
1
2
激发潜能
拓广探究
两条平行直线被第三条直线所截,一对同位角的角平分线有何位置关系?内错角的角平分线、同旁内角的角平分线它们分别又有何位置关系呢?
线的关系
角的关系
判定
性质
课堂小结
位置
数量
合情推理 逆向思维
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的性质
平行线的判定
作业布置
基础题:课本51页随堂练习1题,习题2.5的1,2题
提高题:推广探究题
谢谢观赏
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
