人教版八年级数学上册14.3.2十字相乘法分解因式 教学设计(表格式)
文档属性
| 名称 | 人教版八年级数学上册14.3.2十字相乘法分解因式 教学设计(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 56.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 10:35:43 | ||
图片预览


文档简介
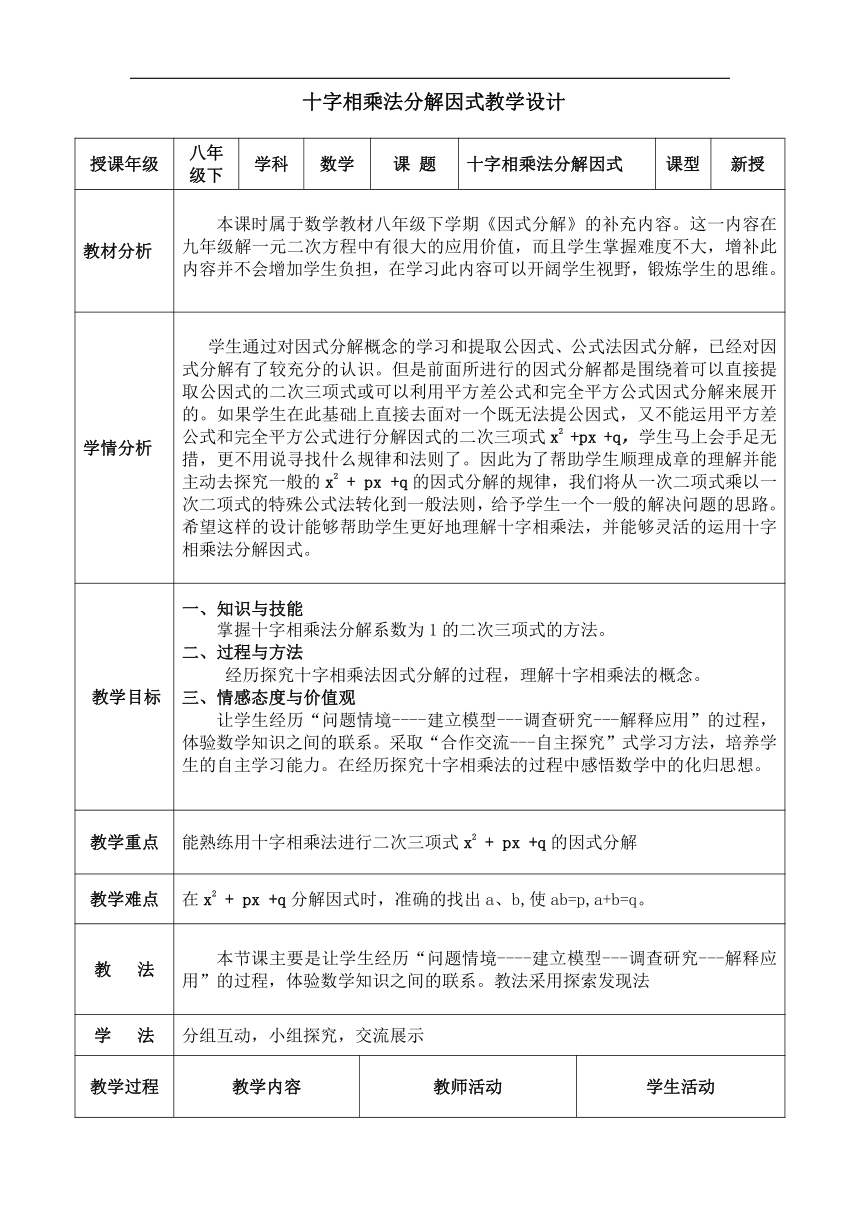
十字相乘法分解因式教学设计
授课年级 八年级下 学科 数学 课 题 十字相乘法分解因式 课型 新授
教材分析 本课时属于数学教材八年级下学期《因式分解》的补充内容。这一内容在九年级解一元二次方程中有很大的应用价值,而且学生掌握难度不大,增补此内容并不会增加学生负担,在学习此内容可以开阔学生视野,锻炼学生的思维。
学情分析 学生通过对因式分解概念的学习和提取公因式、公式法因式分解,已经对因式分解有了较充分的认识。但是前面所进行的因式分解都是围绕着可以直接提取公因式的二次三项式或可以利用平方差公式和完全平方公式因式分解来展开的。如果学生在此基础上直接去面对一个既无法提公因式,又不能运用平方差公式和完全平方公式进行分解因式的二次三项式x2 +px +q,学生马上会手足无措,更不用说寻找什么规律和法则了。因此为了帮助学生顺理成章的理解并能主动去探究一般的x2 + px +q的因式分解的规律,我们将从一次二项式乘以一次二项式的特殊公式法转化到一般法则,给予学生一个一般的解决问题的思路。希望这样的设计能够帮助学生更好地理解十字相乘法,并能够灵活的运用十字相乘法分解因式。
教学目标 一、知识与技能掌握十字相乘法分解系数为1的二次三项式的方法。二、过程与方法 经历探究十字相乘法因式分解的过程,理解十字相乘法的概念。三、情感态度与价值观让学生经历“问题情境----建立模型---调查研究---解释应用”的过程,体验数学知识之间的联系。采取“合作交流---自主探究”式学习方法,培养学生的自主学习能力。在经历探究十字相乘法的过程中感悟数学中的化归思想。
教学重点 能熟练用十字相乘法进行二次三项式x2 + px +q的因式分解
教学难点 在x2 + px +q分解因式时,准确的找出a、b,使ab=p,a+b=q。
教 法 本节课主要是让学生经历“问题情境----建立模型---调查研究---解释应用”的过程,体验数学知识之间的联系。教法采用探索发现法
学 法 分组互动,小组探究,交流展示
教学过程 教学内容 教师活动 学生活动
课前展示精彩一练 计算下列各式: (1)(x+3)(x+4) (2)(x-3) (x+4) (3)(x+3) (x-4) (4)(x-3) (x-4) 教师提问:你有什么快速计算类似以上多项式的诀窍吗? 学生总结规律:两个一次二项式相乘的结果是二次项是x2 ,一次项的系数是两个一次二项式中的常数项的和,常数项相乘作为结果的常数项。
创境激趣导入新知 整式乘法(x+p)(x+q)= x2 +px+pq与分解因式 x2 +px+pq=(x+p)(x+q)互为逆运算 我们可以利用这个规律把一个二次三项式分解因式,那么怎么分解因式呢? 学生思考
自主探究交流展示 1、规律:2、例题 x2 +3x+23、公式x2+(p+q)x+pq=(x+p)(x+q) 4、例题 x2 – 5x –6 5、练习 1)x2 –7x +12 2) x2 –4x – 123)x2 + 8x +12 4) x2 –11x –12 5)x2 +13x +12 6) x2 –x – 126、符号 教师总结:利用十字相乘法分解二次三项式x2 + ax +b,使常数项b=pq,一次项的系数a=p+q,那么 x2+ax+b=x2+(p+q)x+pq=(x+p)(x+q)教师板书讲解并总结步骤:(1)竖分二次项与常数项(2)交叉相乘,积相加(3)检验确定,横写因式教师板书指导教师指导,对答案提问:符号有什么样的规律呢?填空:对于x2 + ax +b =(x+p)(x+q) (1)当b>0时,p、q_____;且p、q的符号与a的符号______.(2)当b<0时,p、q_____;且___________________与a的符号相同. 学生分小组进行讨论总结规律: 把常数项拆成两个数的乘积,而这两个数的和刚好等于一次项的系数认真观察学生在练习本上完成,各组派代表在黑板上写。以小组竞赛的方式完成学生进行讨论,并进行汇报总结
巩固新知拓展提高 (1)x2+3x–4 (2)x2 –3x +4(3)x2 + 6xy –16y2 (4)x2 –11xy+24y2 (5)x2y2 –7xy –18 (6)x4 –13x2 +36 教师进行指导,尤其是第(3)(4)(5)(6)题,与我们前面的类型有不一样的地方。 学生分小组完成练习,遇到问题小组成员之间可以讨论。并总结出规律。
总结反思分享收获 提问:通过这节课的学习你学到了什么? 1.十字相乘法分解因式的公式 x2+(p+q)x+pq=(x+p)(x+q)2.能用十字相乘法分解因式的二次三项式的系数的特点:常数项能分解成两个常数的积,且恰好这两个常数的和等于一次项的系数。
作业 1、若x2 +mx – 12能分解成两个整系数的一次因式乘积,则符合条件的m有多少个? 2、利用十字相乘法分解因式 (1)x2 –5x +6(2)x2 +5x +6 (3)x2 +5x –6(4)x2 – 5x –6 (5)( x – y)2 +( x – y)–6
板书设计 十字相乘法分解因式公式 例题 x2 +3x+2 例题 x2 – 5x –6x2+(p+q)x+pq=(x+p)(x+q) (1)竖分二次项与常数项(2)交叉相乘,积相加(3)检验确定,横写因式
复备教师教学反思
授课年级 八年级下 学科 数学 课 题 十字相乘法分解因式 课型 新授
教材分析 本课时属于数学教材八年级下学期《因式分解》的补充内容。这一内容在九年级解一元二次方程中有很大的应用价值,而且学生掌握难度不大,增补此内容并不会增加学生负担,在学习此内容可以开阔学生视野,锻炼学生的思维。
学情分析 学生通过对因式分解概念的学习和提取公因式、公式法因式分解,已经对因式分解有了较充分的认识。但是前面所进行的因式分解都是围绕着可以直接提取公因式的二次三项式或可以利用平方差公式和完全平方公式因式分解来展开的。如果学生在此基础上直接去面对一个既无法提公因式,又不能运用平方差公式和完全平方公式进行分解因式的二次三项式x2 +px +q,学生马上会手足无措,更不用说寻找什么规律和法则了。因此为了帮助学生顺理成章的理解并能主动去探究一般的x2 + px +q的因式分解的规律,我们将从一次二项式乘以一次二项式的特殊公式法转化到一般法则,给予学生一个一般的解决问题的思路。希望这样的设计能够帮助学生更好地理解十字相乘法,并能够灵活的运用十字相乘法分解因式。
教学目标 一、知识与技能掌握十字相乘法分解系数为1的二次三项式的方法。二、过程与方法 经历探究十字相乘法因式分解的过程,理解十字相乘法的概念。三、情感态度与价值观让学生经历“问题情境----建立模型---调查研究---解释应用”的过程,体验数学知识之间的联系。采取“合作交流---自主探究”式学习方法,培养学生的自主学习能力。在经历探究十字相乘法的过程中感悟数学中的化归思想。
教学重点 能熟练用十字相乘法进行二次三项式x2 + px +q的因式分解
教学难点 在x2 + px +q分解因式时,准确的找出a、b,使ab=p,a+b=q。
教 法 本节课主要是让学生经历“问题情境----建立模型---调查研究---解释应用”的过程,体验数学知识之间的联系。教法采用探索发现法
学 法 分组互动,小组探究,交流展示
教学过程 教学内容 教师活动 学生活动
课前展示精彩一练 计算下列各式: (1)(x+3)(x+4) (2)(x-3) (x+4) (3)(x+3) (x-4) (4)(x-3) (x-4) 教师提问:你有什么快速计算类似以上多项式的诀窍吗? 学生总结规律:两个一次二项式相乘的结果是二次项是x2 ,一次项的系数是两个一次二项式中的常数项的和,常数项相乘作为结果的常数项。
创境激趣导入新知 整式乘法(x+p)(x+q)= x2 +px+pq与分解因式 x2 +px+pq=(x+p)(x+q)互为逆运算 我们可以利用这个规律把一个二次三项式分解因式,那么怎么分解因式呢? 学生思考
自主探究交流展示 1、规律:2、例题 x2 +3x+23、公式x2+(p+q)x+pq=(x+p)(x+q) 4、例题 x2 – 5x –6 5、练习 1)x2 –7x +12 2) x2 –4x – 123)x2 + 8x +12 4) x2 –11x –12 5)x2 +13x +12 6) x2 –x – 126、符号 教师总结:利用十字相乘法分解二次三项式x2 + ax +b,使常数项b=pq,一次项的系数a=p+q,那么 x2+ax+b=x2+(p+q)x+pq=(x+p)(x+q)教师板书讲解并总结步骤:(1)竖分二次项与常数项(2)交叉相乘,积相加(3)检验确定,横写因式教师板书指导教师指导,对答案提问:符号有什么样的规律呢?填空:对于x2 + ax +b =(x+p)(x+q) (1)当b>0时,p、q_____;且p、q的符号与a的符号______.(2)当b<0时,p、q_____;且___________________与a的符号相同. 学生分小组进行讨论总结规律: 把常数项拆成两个数的乘积,而这两个数的和刚好等于一次项的系数认真观察学生在练习本上完成,各组派代表在黑板上写。以小组竞赛的方式完成学生进行讨论,并进行汇报总结
巩固新知拓展提高 (1)x2+3x–4 (2)x2 –3x +4(3)x2 + 6xy –16y2 (4)x2 –11xy+24y2 (5)x2y2 –7xy –18 (6)x4 –13x2 +36 教师进行指导,尤其是第(3)(4)(5)(6)题,与我们前面的类型有不一样的地方。 学生分小组完成练习,遇到问题小组成员之间可以讨论。并总结出规律。
总结反思分享收获 提问:通过这节课的学习你学到了什么? 1.十字相乘法分解因式的公式 x2+(p+q)x+pq=(x+p)(x+q)2.能用十字相乘法分解因式的二次三项式的系数的特点:常数项能分解成两个常数的积,且恰好这两个常数的和等于一次项的系数。
作业 1、若x2 +mx – 12能分解成两个整系数的一次因式乘积,则符合条件的m有多少个? 2、利用十字相乘法分解因式 (1)x2 –5x +6(2)x2 +5x +6 (3)x2 +5x –6(4)x2 – 5x –6 (5)( x – y)2 +( x – y)–6
板书设计 十字相乘法分解因式公式 例题 x2 +3x+2 例题 x2 – 5x –6x2+(p+q)x+pq=(x+p)(x+q) (1)竖分二次项与常数项(2)交叉相乘,积相加(3)检验确定,横写因式
复备教师教学反思
