人教版八年级数学上册12.2三角形全等的判定(3)ASA AAS 教案(表格式)
文档属性
| 名称 | 人教版八年级数学上册12.2三角形全等的判定(3)ASA AAS 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 389.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 00:00:00 | ||
图片预览

文档简介
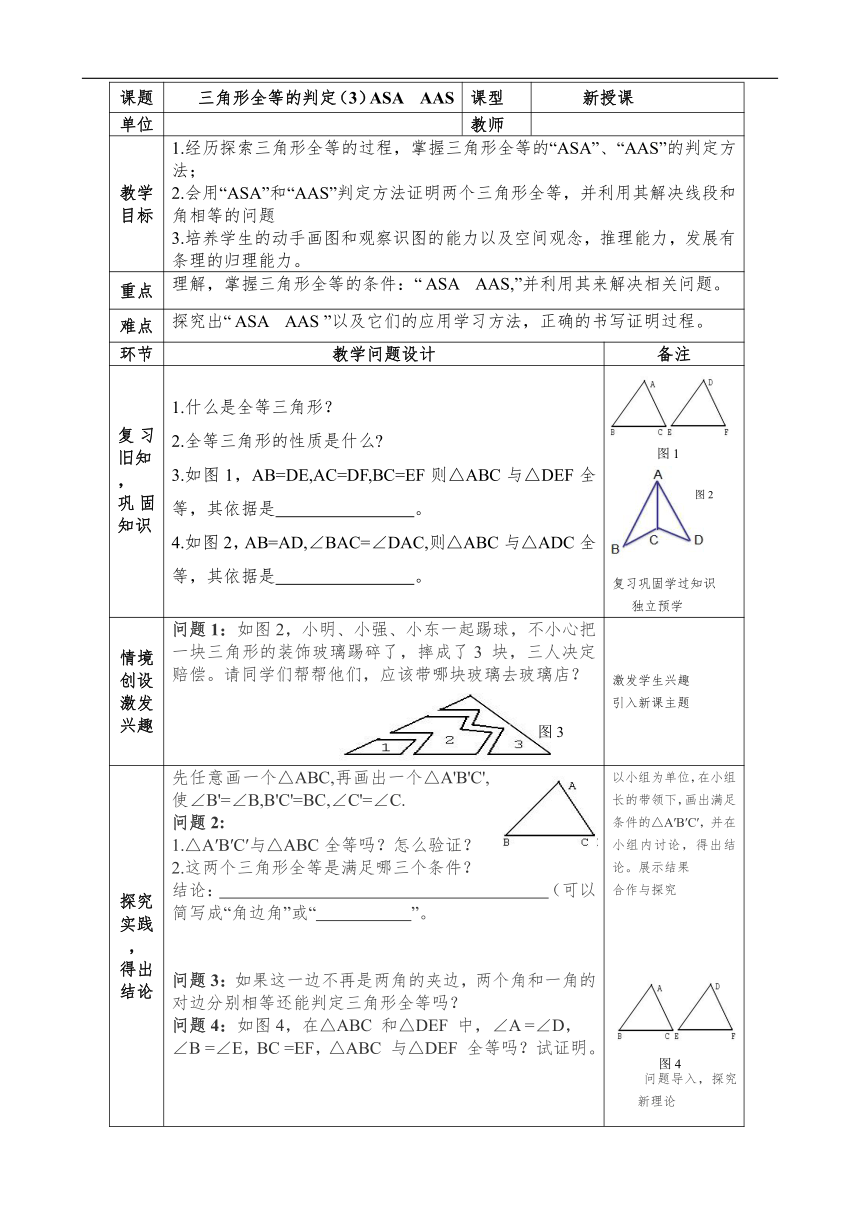
课题 三角形全等的判定(3)ASA AAS 课型 新授课
单位 教师
教学目标 1.经历探索三角形全等的过程,掌握三角形全等的“ASA”、“AAS”的判定方法;2.会用“ASA”和“AAS”判定方法证明两个三角形全等,并利用其解决线段和角相等的问题 3.培养学生的动手画图和观察识图的能力以及空间观念,推理能力,发展有条理的归理能力。
重点 理解,掌握三角形全等的条件:“ ASA AAS,”并利用其来解决相关问题。
难点 探究出“ ASA AAS ”以及它们的应用学习方法,正确的书写证明过程。
环节 教学问题设计 备注
复习旧知,巩固知识 什么是全等三角形?全等三角形的性质是什么 如图1,AB=DE,AC=DF,BC=EF则△ABC与△DEF全等,其依据是 。4.如图2,AB=AD,∠BAC=∠DAC,则△ABC与△ADC全等,其依据是 。 复习巩固学过知识 独立预学
情境创设激发兴趣 问题1:如图2,小明、小强、小东一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了3 块,三人决定赔偿。请同学们帮帮他们,应该带哪块玻璃去玻璃店? 激发学生兴趣引入新课主题
探究实践,得出结论 先任意画一个△ABC,再画出一个△A'B'C',使∠B'=∠B,B'C'=BC,∠C'=∠C.问题2:1.△A′B′C′与△ABC全等吗?怎么验证? 2.这两个三角形全等是满足哪三个条件?结论: (可以简写成“角边角”或“ ”。问题3:如果这一边不再是两角的夹边,两个角和一角的对边分别相等还能判定三角形全等吗?问题4:如图4,在△ABC 和△DEF 中,∠A =∠D,∠B =∠E,BC =EF,△ABC 与△DEF 全等吗?试证明。 以小组为单位,在小组长的带领下,画出满足条件的△A′B′C′,并在小组内讨论,得出结论。展示结果合作与探究
精讲例题,理解新知 例:如图5,点D 在AB上,点E 在AC上,AB =AC,∠B =∠C.求证:△ABE≌△ACD.变式1:“∠B =∠C”变成“∠AEB =∠ADC”,求证:△ABE≌△ACD 进一步理解定理,加深理解
拓展延伸加强应用 变式2:点D 在AB上,点E 在AC上,AB =AC,AE=AD,∠A=63°,∠B=27°。求的度数(2)判断CD与AB的位置关系,并加以证明变式3:点D 在AB上,点E 在AC上,AB =AC,AE=AD.求证:(1)BD=EC (2)△BCE≌△CBD. 变式训练,举一反三,加深理解
归纳小结 本节课你学到了什么?有什么收获?还有那些困惑? 知识系统化
随堂检测 1.两角和它们的 对应相等的两个三角形全等,简写为“ ”或“ ”。2.两角分别相等且其中一组等角的 相等的两个三角形全等。简写“ ”或“ ”。3.如图,AE=AD,∠B =∠C,EC=6,AD=4,则AC= 。4.如图,已知BC=DF,∠B=∠F,AC∥DE,求证:△ABC≌△EFD证明: ∵AC∥DE∴∠ACB=∠EDF( )在△ABC和△EFD中 ∴△ABC≌△EFD( ) 查看学习效果
图1
图2
图3
图4
问题导入,探究新理论
图5
单位 教师
教学目标 1.经历探索三角形全等的过程,掌握三角形全等的“ASA”、“AAS”的判定方法;2.会用“ASA”和“AAS”判定方法证明两个三角形全等,并利用其解决线段和角相等的问题 3.培养学生的动手画图和观察识图的能力以及空间观念,推理能力,发展有条理的归理能力。
重点 理解,掌握三角形全等的条件:“ ASA AAS,”并利用其来解决相关问题。
难点 探究出“ ASA AAS ”以及它们的应用学习方法,正确的书写证明过程。
环节 教学问题设计 备注
复习旧知,巩固知识 什么是全等三角形?全等三角形的性质是什么 如图1,AB=DE,AC=DF,BC=EF则△ABC与△DEF全等,其依据是 。4.如图2,AB=AD,∠BAC=∠DAC,则△ABC与△ADC全等,其依据是 。 复习巩固学过知识 独立预学
情境创设激发兴趣 问题1:如图2,小明、小强、小东一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了3 块,三人决定赔偿。请同学们帮帮他们,应该带哪块玻璃去玻璃店? 激发学生兴趣引入新课主题
探究实践,得出结论 先任意画一个△ABC,再画出一个△A'B'C',使∠B'=∠B,B'C'=BC,∠C'=∠C.问题2:1.△A′B′C′与△ABC全等吗?怎么验证? 2.这两个三角形全等是满足哪三个条件?结论: (可以简写成“角边角”或“ ”。问题3:如果这一边不再是两角的夹边,两个角和一角的对边分别相等还能判定三角形全等吗?问题4:如图4,在△ABC 和△DEF 中,∠A =∠D,∠B =∠E,BC =EF,△ABC 与△DEF 全等吗?试证明。 以小组为单位,在小组长的带领下,画出满足条件的△A′B′C′,并在小组内讨论,得出结论。展示结果合作与探究
精讲例题,理解新知 例:如图5,点D 在AB上,点E 在AC上,AB =AC,∠B =∠C.求证:△ABE≌△ACD.变式1:“∠B =∠C”变成“∠AEB =∠ADC”,求证:△ABE≌△ACD 进一步理解定理,加深理解
拓展延伸加强应用 变式2:点D 在AB上,点E 在AC上,AB =AC,AE=AD,∠A=63°,∠B=27°。求的度数(2)判断CD与AB的位置关系,并加以证明变式3:点D 在AB上,点E 在AC上,AB =AC,AE=AD.求证:(1)BD=EC (2)△BCE≌△CBD. 变式训练,举一反三,加深理解
归纳小结 本节课你学到了什么?有什么收获?还有那些困惑? 知识系统化
随堂检测 1.两角和它们的 对应相等的两个三角形全等,简写为“ ”或“ ”。2.两角分别相等且其中一组等角的 相等的两个三角形全等。简写“ ”或“ ”。3.如图,AE=AD,∠B =∠C,EC=6,AD=4,则AC= 。4.如图,已知BC=DF,∠B=∠F,AC∥DE,求证:△ABC≌△EFD证明: ∵AC∥DE∴∠ACB=∠EDF( )在△ABC和△EFD中 ∴△ABC≌△EFD( ) 查看学习效果
图1
图2
图3
图4
问题导入,探究新理论
图5
