人教版八年级数学上册第十一章 三角形数学活动 平面镶嵌教学设计
文档属性
| 名称 | 人教版八年级数学上册第十一章 三角形数学活动 平面镶嵌教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 46.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 00:00:00 | ||
图片预览

文档简介
数学活动-----平面镶嵌
教学目标:
1.了解平面镶嵌的概念.
2.了解多边形能够平面镶嵌的条件;体会从特殊到
一般,从简单到复杂的研究问题的思路与方法.
3.积极参加数学活动,在数学活动中培养敢于动手,
合作交流,归纳反思,勇于质疑的品质;锻炼克
服困难的意志,体验获得成功的乐趣,建立学好
数学的信心,积累数学活动的一些基本经验.
教学重难点:
探究多边形镶嵌的条件.
教学过程
复习回顾:
1、 n边形内角和公式:
从n边形一个顶点出发可以得到__________条对角线,把多边形分成________个三角形,所以n边形内角和为_________。
边数 正三角形 正四边形 正五边形 正六边形
内角和
各角度数
2、 正n边形个内角度数
新课探究:
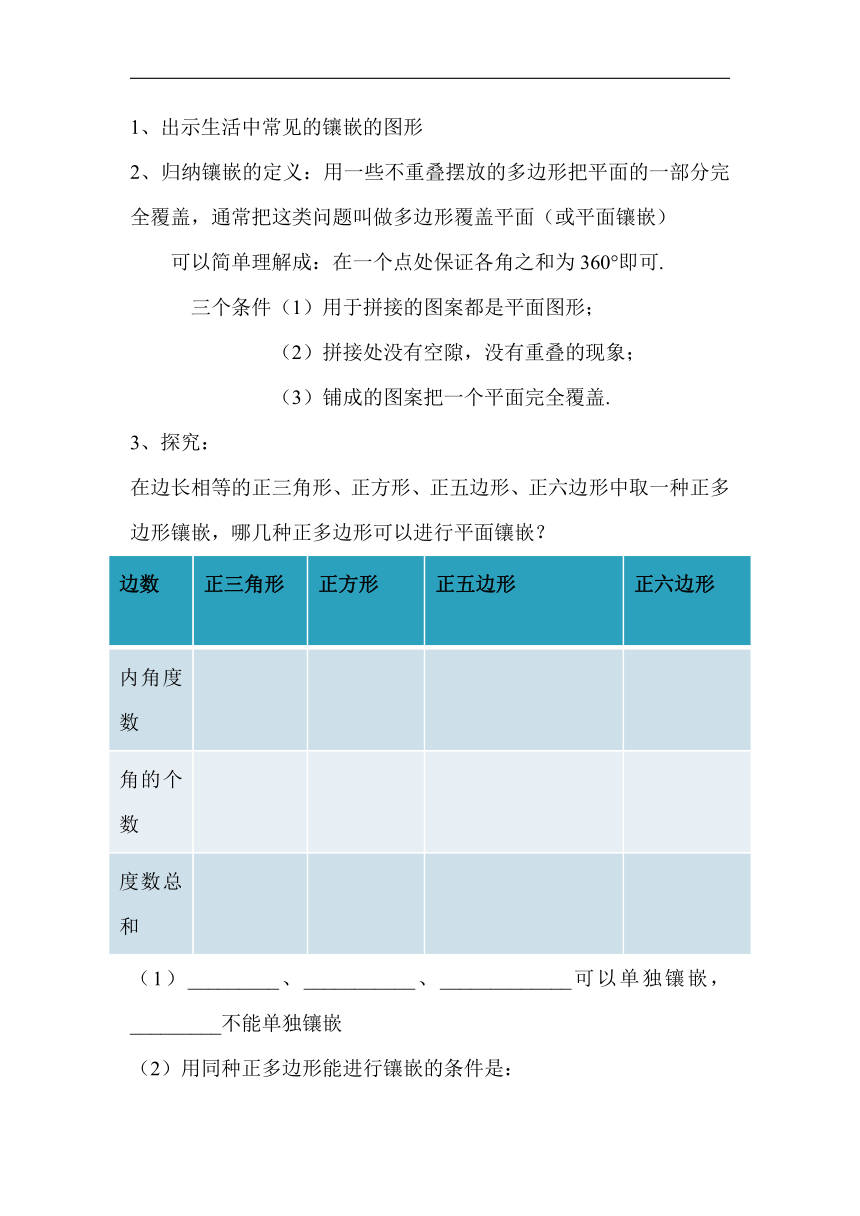
1、出示生活中常见的镶嵌的图形
2、归纳镶嵌的定义:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做多边形覆盖平面(或平面镶嵌)
可以简单理解成:在一个点处保证各角之和为360°即可.
三个条件(1)用于拼接的图案都是平面图形;
(2)拼接处没有空隙,没有重叠的现象;
(3)铺成的图案把一个平面完全覆盖.
3、探究:
在边长相等的正三角形、正方形、正五边形、正六边形中取一种正多边形镶嵌,哪几种正多边形可以进行平面镶嵌?
边数 正三角形 正方形 正五边形 正六边形
内角度数
角的个数
度数总和
(1)_________、___________、_____________可以单独镶嵌,_________不能单独镶嵌
(2)用同种正多边形能进行镶嵌的条件是:
___________________________
探究4 在边长相等的正三角形、正方形、正五边形、正六边形中取两种正多边形镶嵌,哪两种正多边形可以进行平面镶嵌?
组合 正三角形正方形 正三角形正五边形 正三角形正六边形 正方形正五边形 正方形正六边形 正五边形正六边形
图形1内角度数
图形2内角度数
内角个数
度数之和
设 n 表示正多边形的边数.
(1) 、 能镶嵌,___________________________不能镶嵌.
(2)用两种正多边形进行镶嵌的条件是:
a x° + b y° =360,其中a,b表示正多边形的个数,
x°,y°表示正多边形每个内角的度数
探究5用形状、大小相同的三角形能否进行平面镶嵌?四边形呢?
结论:两者均可以进行平面镶嵌,满足顶点处各角度数之和是360° 2*180°=360° 4*90°=360°
课堂小结:
(1)解决本节课中的问题,用到了什么数学知识?
(2)满足镶嵌的条件:让顶点处各角度数之和为360°即可
作业:练习册。
教学目标:
1.了解平面镶嵌的概念.
2.了解多边形能够平面镶嵌的条件;体会从特殊到
一般,从简单到复杂的研究问题的思路与方法.
3.积极参加数学活动,在数学活动中培养敢于动手,
合作交流,归纳反思,勇于质疑的品质;锻炼克
服困难的意志,体验获得成功的乐趣,建立学好
数学的信心,积累数学活动的一些基本经验.
教学重难点:
探究多边形镶嵌的条件.
教学过程
复习回顾:
1、 n边形内角和公式:
从n边形一个顶点出发可以得到__________条对角线,把多边形分成________个三角形,所以n边形内角和为_________。
边数 正三角形 正四边形 正五边形 正六边形
内角和
各角度数
2、 正n边形个内角度数
新课探究:
1、出示生活中常见的镶嵌的图形
2、归纳镶嵌的定义:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做多边形覆盖平面(或平面镶嵌)
可以简单理解成:在一个点处保证各角之和为360°即可.
三个条件(1)用于拼接的图案都是平面图形;
(2)拼接处没有空隙,没有重叠的现象;
(3)铺成的图案把一个平面完全覆盖.
3、探究:
在边长相等的正三角形、正方形、正五边形、正六边形中取一种正多边形镶嵌,哪几种正多边形可以进行平面镶嵌?
边数 正三角形 正方形 正五边形 正六边形
内角度数
角的个数
度数总和
(1)_________、___________、_____________可以单独镶嵌,_________不能单独镶嵌
(2)用同种正多边形能进行镶嵌的条件是:
___________________________
探究4 在边长相等的正三角形、正方形、正五边形、正六边形中取两种正多边形镶嵌,哪两种正多边形可以进行平面镶嵌?
组合 正三角形正方形 正三角形正五边形 正三角形正六边形 正方形正五边形 正方形正六边形 正五边形正六边形
图形1内角度数
图形2内角度数
内角个数
度数之和
设 n 表示正多边形的边数.
(1) 、 能镶嵌,___________________________不能镶嵌.
(2)用两种正多边形进行镶嵌的条件是:
a x° + b y° =360,其中a,b表示正多边形的个数,
x°,y°表示正多边形每个内角的度数
探究5用形状、大小相同的三角形能否进行平面镶嵌?四边形呢?
结论:两者均可以进行平面镶嵌,满足顶点处各角度数之和是360° 2*180°=360° 4*90°=360°
课堂小结:
(1)解决本节课中的问题,用到了什么数学知识?
(2)满足镶嵌的条件:让顶点处各角度数之和为360°即可
作业:练习册。
