2021—2022学年人教版八年级数学下册18.2.3正方形课后练习题 (Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.2.3正方形课后练习题 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 298.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 19:08:09 | ||
图片预览

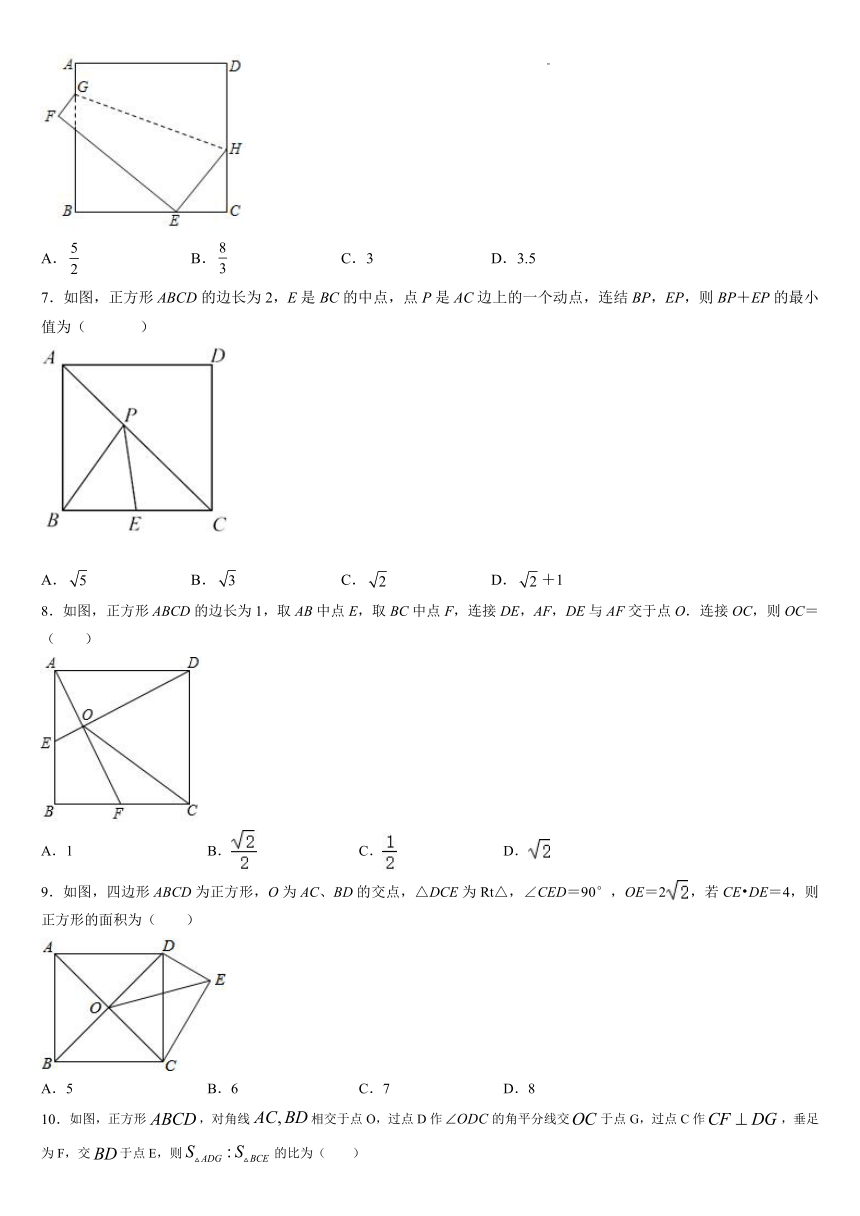
文档简介
18.2.3正方形 课后练习题
一、选择题
1.下列说法正确的是( )
A.平行四边形的对角线互相平分且相等 B.矩形的对角线相等且互相平分
C.菱形的对角线互相垂直且相等 D.正方形的对角线是正方形的对称轴
2.如图,在正方形ABCD中,点E、F分别在边CD、AD上,BE与CF交于点G.若BC=8,DE=AF=2,则FG的长为( )
A. B. C. D.
3.如图,在正方形ABCD中,点E,F分别为AB,AD的中点,CE,BF相交于点G,AB=2,则CG=( )
A. B. C. D.
4.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A.4﹣2 B.3﹣4 C.1 D.
5.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是( )
A.13 B.14 C.15 D.16
6.如图,正方形ABCD的边长为6,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE:EC=2:1,则线段CH的长是( )
A. B. C.3 D.3.5
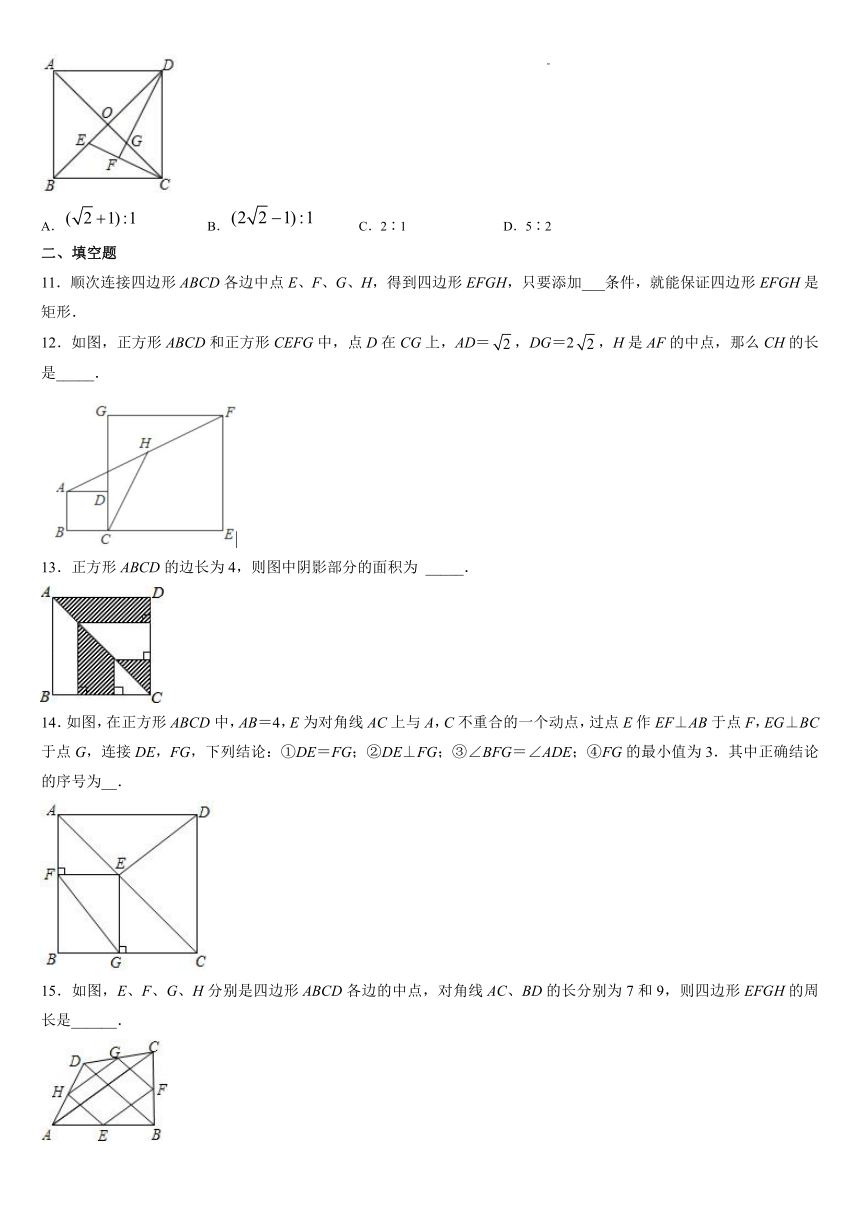
7.如图,正方形ABCD的边长为2,E是BC的中点,点P是AC边上的一个动点,连结BP,EP,则BP+EP的最小值为( )
A. B. C. D.+1
8.如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE,AF,DE与AF交于点O.连接OC,则OC=( )
A.1 B. C. D.
9.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE DE=4,则正方形的面积为( )
A.5 B.6 C.7 D.8
10.如图,正方形,对角线相交于点O,过点D作的角平分线交于点G,过点C作,垂足为F,交于点E,则的比为( )
A. B. C.2∶1 D.5∶2
二、填空题
11.顺次连接四边形ABCD各边中点E、F、G、H,得到四边形EFGH,只要添加___条件,就能保证四边形EFGH是矩形.
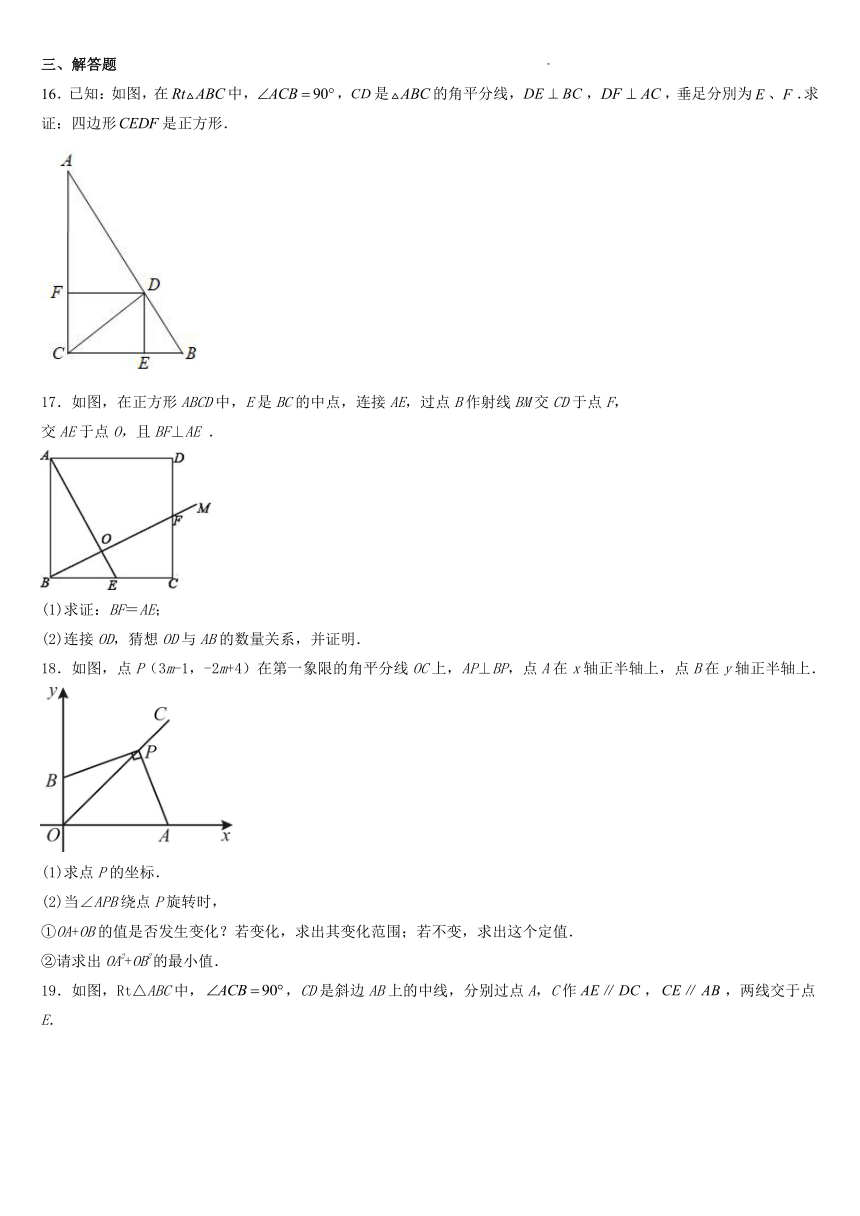
12.如图,正方形ABCD和正方形CEFG中,点D在CG上,AD=,DG=2,H是AF的中点,那么CH的长是_____.
13.正方形ABCD的边长为4,则图中阴影部分的面积为 _____.
14.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论的序号为__.
15.如图,E、F、G、H分别是四边形ABCD各边的中点,对角线AC、BD的长分别为7和9,则四边形EFGH的周长是______.
三、解答题
16.已知:如图,在中,,是的角平分线,,,垂足分別为、.求证:四边形是正方形.
17.如图,在正方形ABCD中,E是BC的中点,连接AE,过点B作射线BM交CD于点F,
交AE于点O,且BF⊥AE .
(1)求证:BF=AE;
(2)连接OD,猜想OD与AB的数量关系,并证明.
18.如图,点P(3m-1,-2m+4)在第一象限的角平分线OC上,AP⊥BP,点A在x轴正半轴上,点B在y轴正半轴上.
(1)求点P的坐标.
(2)当∠APB绕点P旋转时,
①OA+OB的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.
②请求出OA2+OB2的最小值.
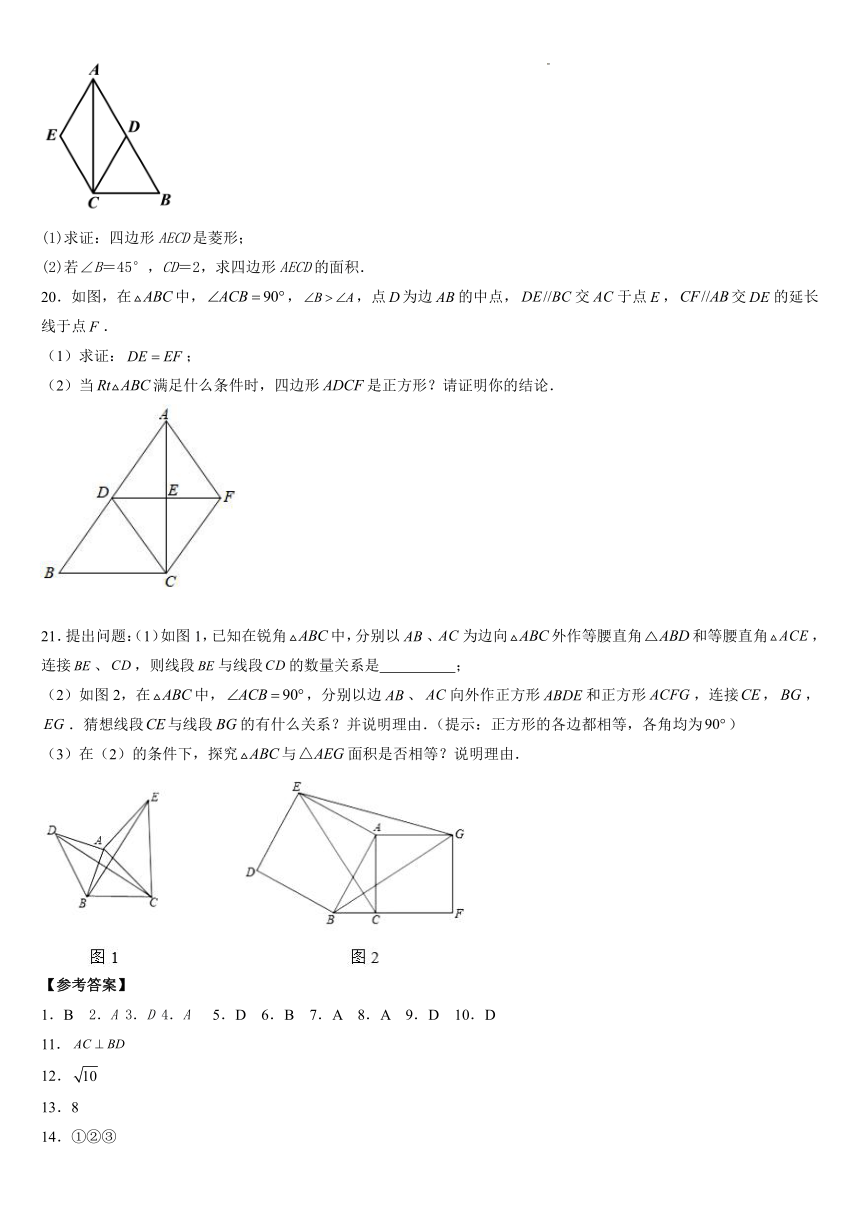
19.如图,Rt△ABC中,,CD是斜边AB上的中线,分别过点A,C作,,两线交于点E.
(1)求证:四边形AECD是菱形;
(2)若∠B=45°,CD=2,求四边形AECD的面积.
20.如图,在中,,,点为边的中点,交于点,交的延长线于点.
(1)求证:;
(2)当满足什么条件时,四边形是正方形?请证明你的结论.
21.提出问题:(1)如图1,已知在锐角中,分别以、为边向外作等腰直角和等腰直角,连接、,则线段与线段的数量关系是 ;
(2)如图2,在中,,分别以边、向外作正方形和正方形,连接,,.猜想线段与线段的有什么关系?并说明理由.(提示:正方形的各边都相等,各角均为)
(3)在(2)的条件下,探究与面积是否相等?说明理由.
【参考答案】
1.B 2.A 3.D 4.A 5.D 6.B 7.A 8.A 9.D 10.D
11.
12.
13.8
14.①②③
15.16
16.证明:∵平分,,,
∴,,,
又∵,
∴四边形是矩形,
∵,
∴矩形是正方形.
17.(1)证明:在正方形ABCD中,∠ABC=∠C=90°,AB=BC,
∴∠BAE+∠AEB=90°,
∵BF⊥AE,
∴∠EOB=90°,
∴∠CBF+∠AEB=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF,
∴BF=AE;
(2)解:OD=AB,理由如下:
如图,延长AD交射线BM于点G,
由(1)得:△ABE≌△BCF,
∴BE=CF,
∵E是BC的中点,
∴,
∴CF=DF,
∵AD∥BC,
∴∠DGF=∠CBF,
在△DGF和△CBF中,
∵∠DGF=∠CBF,∠DFG=∠BFC,DF=CF,
∴△DGF≌△CBF,
∴DG=BC,
∴DG=AD,即OD为△AOG的中线,
∵BF⊥AE,
∴.
18.(1)解:∵点P (3m-1,-2m+4)在第一象限的角平分线OC上,
∴3m-1=-2m+4,
∴m=1,
∴P(2,2);
(2)①过点P作PM⊥y轴于M,PN⊥OA于N.
∵∠PMO=∠PNO=∠MON=90°,
∴四边形OMPN是矩形,
∵OP平分∠MON,PM⊥OM,PN⊥ON,
∴PM=PN,
∴四边形OMPN是正方形,
∵P(2,2),
∴PM=PN=OM=ON=2,
∵AP⊥BP,
∴∠APB=∠MPN=90°,
∴∠MPB+∠BPN=∠BPN+∠NPA=90°,
∴∠MPB=∠NPA,
在△PMB和△PNA中,
,
∴△PMB≌△PNA(ASA),
∴BM=AN,
∴OB+OA=OM-BM+ON+AN=2OM=4.
②连接AB,
∵∠AOB=90°,
∴OA2+OB2=AB2.
∵∠BPA=90°,
∴AB2=PA2+PB2=2PA2,
∴OA2+OB2=2PA2,
当PA最小时,OA2+OB2也最小.
根据垂线段最短原理,PA最小值为2.
∴OA2+OB2的最小值为8.
19.(1)证明:∵AE∥DC,CE∥AB,
∴四边形AECD是平行四边形,
∵Rt△ABC中,,CD是斜边AB上的中线,
∴CD=AD,
∴四边形AECD是菱形.
(2)解:∵Rt△ABC中,,CD是斜边AB上的中线,
∴CD=AD=DB=2,
∴∠B=∠BCD=45°,
∴∠CDA=∠B+∠BCD=90°,
∴四边形AECD是正方形,
∴ S正方形AECD= CD 2=4.
21.解:
(1)如图(1)所示:
∵点,,
∴,,
∵四边形OBCD是矩形,
∴,,
∴点;
(2)如图(2)所示:
∵四边形ABCD是菱形,
∴,,
∵点,,
∴,,
∴点,点;
(3)如图(3)所示:
∵四边形OBCD是正方形,
∴,
∵点,
∴,
∴,
∴点,点.
23.解:(1)∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AC=AE,∠DAB=∠CAE=90°,
∴∠DAC=∠BAE,
∴△ADC≌△ABE(SAS),
∴BE=CD,
故答案为: ;
(2),;理由如下:
如图,设AB与CE的交点为P,
∵四边形ACFG和四边形ABDE是正方形,
∴AB=AE,AC=AG,∠EAB=∠GAC=90°,,
,
,
在和中,,
,
,,
,,
,
;
即:,;
(3)如图,过点作交延长线于;
,
,,
,
在和中,,
,
,
,
一、选择题
1.下列说法正确的是( )
A.平行四边形的对角线互相平分且相等 B.矩形的对角线相等且互相平分
C.菱形的对角线互相垂直且相等 D.正方形的对角线是正方形的对称轴
2.如图,在正方形ABCD中,点E、F分别在边CD、AD上,BE与CF交于点G.若BC=8,DE=AF=2,则FG的长为( )
A. B. C. D.
3.如图,在正方形ABCD中,点E,F分别为AB,AD的中点,CE,BF相交于点G,AB=2,则CG=( )
A. B. C. D.
4.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A.4﹣2 B.3﹣4 C.1 D.
5.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是( )
A.13 B.14 C.15 D.16
6.如图,正方形ABCD的边长为6,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE:EC=2:1,则线段CH的长是( )
A. B. C.3 D.3.5
7.如图,正方形ABCD的边长为2,E是BC的中点,点P是AC边上的一个动点,连结BP,EP,则BP+EP的最小值为( )
A. B. C. D.+1
8.如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE,AF,DE与AF交于点O.连接OC,则OC=( )
A.1 B. C. D.
9.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE DE=4,则正方形的面积为( )
A.5 B.6 C.7 D.8
10.如图,正方形,对角线相交于点O,过点D作的角平分线交于点G,过点C作,垂足为F,交于点E,则的比为( )
A. B. C.2∶1 D.5∶2
二、填空题
11.顺次连接四边形ABCD各边中点E、F、G、H,得到四边形EFGH,只要添加___条件,就能保证四边形EFGH是矩形.
12.如图,正方形ABCD和正方形CEFG中,点D在CG上,AD=,DG=2,H是AF的中点,那么CH的长是_____.
13.正方形ABCD的边长为4,则图中阴影部分的面积为 _____.
14.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论的序号为__.
15.如图,E、F、G、H分别是四边形ABCD各边的中点,对角线AC、BD的长分别为7和9,则四边形EFGH的周长是______.
三、解答题
16.已知:如图,在中,,是的角平分线,,,垂足分別为、.求证:四边形是正方形.
17.如图,在正方形ABCD中,E是BC的中点,连接AE,过点B作射线BM交CD于点F,
交AE于点O,且BF⊥AE .
(1)求证:BF=AE;
(2)连接OD,猜想OD与AB的数量关系,并证明.
18.如图,点P(3m-1,-2m+4)在第一象限的角平分线OC上,AP⊥BP,点A在x轴正半轴上,点B在y轴正半轴上.
(1)求点P的坐标.
(2)当∠APB绕点P旋转时,
①OA+OB的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.
②请求出OA2+OB2的最小值.
19.如图,Rt△ABC中,,CD是斜边AB上的中线,分别过点A,C作,,两线交于点E.
(1)求证:四边形AECD是菱形;
(2)若∠B=45°,CD=2,求四边形AECD的面积.
20.如图,在中,,,点为边的中点,交于点,交的延长线于点.
(1)求证:;
(2)当满足什么条件时,四边形是正方形?请证明你的结论.
21.提出问题:(1)如图1,已知在锐角中,分别以、为边向外作等腰直角和等腰直角,连接、,则线段与线段的数量关系是 ;
(2)如图2,在中,,分别以边、向外作正方形和正方形,连接,,.猜想线段与线段的有什么关系?并说明理由.(提示:正方形的各边都相等,各角均为)
(3)在(2)的条件下,探究与面积是否相等?说明理由.
【参考答案】
1.B 2.A 3.D 4.A 5.D 6.B 7.A 8.A 9.D 10.D
11.
12.
13.8
14.①②③
15.16
16.证明:∵平分,,,
∴,,,
又∵,
∴四边形是矩形,
∵,
∴矩形是正方形.
17.(1)证明:在正方形ABCD中,∠ABC=∠C=90°,AB=BC,
∴∠BAE+∠AEB=90°,
∵BF⊥AE,
∴∠EOB=90°,
∴∠CBF+∠AEB=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF,
∴BF=AE;
(2)解:OD=AB,理由如下:
如图,延长AD交射线BM于点G,
由(1)得:△ABE≌△BCF,
∴BE=CF,
∵E是BC的中点,
∴,
∴CF=DF,
∵AD∥BC,
∴∠DGF=∠CBF,
在△DGF和△CBF中,
∵∠DGF=∠CBF,∠DFG=∠BFC,DF=CF,
∴△DGF≌△CBF,
∴DG=BC,
∴DG=AD,即OD为△AOG的中线,
∵BF⊥AE,
∴.
18.(1)解:∵点P (3m-1,-2m+4)在第一象限的角平分线OC上,
∴3m-1=-2m+4,
∴m=1,
∴P(2,2);
(2)①过点P作PM⊥y轴于M,PN⊥OA于N.
∵∠PMO=∠PNO=∠MON=90°,
∴四边形OMPN是矩形,
∵OP平分∠MON,PM⊥OM,PN⊥ON,
∴PM=PN,
∴四边形OMPN是正方形,
∵P(2,2),
∴PM=PN=OM=ON=2,
∵AP⊥BP,
∴∠APB=∠MPN=90°,
∴∠MPB+∠BPN=∠BPN+∠NPA=90°,
∴∠MPB=∠NPA,
在△PMB和△PNA中,
,
∴△PMB≌△PNA(ASA),
∴BM=AN,
∴OB+OA=OM-BM+ON+AN=2OM=4.
②连接AB,
∵∠AOB=90°,
∴OA2+OB2=AB2.
∵∠BPA=90°,
∴AB2=PA2+PB2=2PA2,
∴OA2+OB2=2PA2,
当PA最小时,OA2+OB2也最小.
根据垂线段最短原理,PA最小值为2.
∴OA2+OB2的最小值为8.
19.(1)证明:∵AE∥DC,CE∥AB,
∴四边形AECD是平行四边形,
∵Rt△ABC中,,CD是斜边AB上的中线,
∴CD=AD,
∴四边形AECD是菱形.
(2)解:∵Rt△ABC中,,CD是斜边AB上的中线,
∴CD=AD=DB=2,
∴∠B=∠BCD=45°,
∴∠CDA=∠B+∠BCD=90°,
∴四边形AECD是正方形,
∴ S正方形AECD= CD 2=4.
21.解:
(1)如图(1)所示:
∵点,,
∴,,
∵四边形OBCD是矩形,
∴,,
∴点;
(2)如图(2)所示:
∵四边形ABCD是菱形,
∴,,
∵点,,
∴,,
∴点,点;
(3)如图(3)所示:
∵四边形OBCD是正方形,
∴,
∵点,
∴,
∴,
∴点,点.
23.解:(1)∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AC=AE,∠DAB=∠CAE=90°,
∴∠DAC=∠BAE,
∴△ADC≌△ABE(SAS),
∴BE=CD,
故答案为: ;
(2),;理由如下:
如图,设AB与CE的交点为P,
∵四边形ACFG和四边形ABDE是正方形,
∴AB=AE,AC=AG,∠EAB=∠GAC=90°,,
,
,
在和中,,
,
,,
,,
,
;
即:,;
(3)如图,过点作交延长线于;
,
,,
,
在和中,,
,
,
,
