2021-2022学年人教版数学八年级下册18.2.1 矩形(性质、应用、折叠问题)课件(19张)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册18.2.1 矩形(性质、应用、折叠问题)课件(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 445.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
18.2.1 矩形
(1)矩形的性质和矩形性质的应用
(2)矩形中的折叠问题
人教版数学八级下册
矩形的性质和矩形性质的应用
导入观察下面图形,长方形在生活中无处不在.你还能举出其他的例子吗?思考长方形跟我们前面学行四边形有什么关系? 利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察。
矩形
观察在不断地改变图形的一个内角的大小过程中,图形的形状是否发生了变化?思考当这个角变成直角时,那么得到的是一个什么图形?
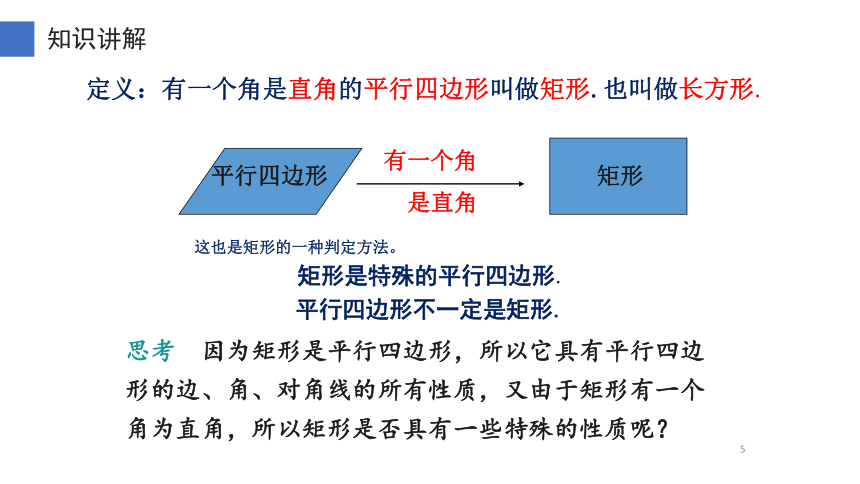
知识讲解定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.平行四边形矩形有一个角是直角矩形是特殊的平行四边形.平行四边形不一定是矩形.思考因为矩形是平行四边形,所以它具有平行四边形的边、角、对角线的所有性质,又由于矩形有一个角为直角,所以矩形是否具有一些特殊的性质呢?这也是矩形的一种判定方法。活动与探究(温馨提示:规范操作、注意安全)
知识讲解
难点突破
猜想 矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,∠B=90°.
求证: ∠B=∠C=∠D=∠A=90°.
A
B
C
D
证明:∵四边形ABCD是矩形,
∴∠B=∠D,∠C=∠A, AB∥DC.
∴∠B+∠C=180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B=∠C=∠D=∠A =90°.
知识讲解矩形的四个角都是直角.矩形除了具有平行四边形所有性质,还具有特殊性质:几何语言:∵ 四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°(矩形的四个角都是直角).课堂练习难点巩固例如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE,垂足为F.求证:DF=DC.ACDEF证明:连接DE.∵AD=AE,∴∠AED=∠ADE.∵四边形ABCD是矩形,∴AD∥BC,∠C=90°.∴∠ADE=∠DEC,∴∠DEC=∠AED.又∵DF⊥AE, ∴∠DFE=∠C=90°.B又∵DE=DE,∴△DFE≌△DCE,∴DF=DC.课堂小结定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.矩形是特殊的平行四边形平行四边形不一定是矩形.矩形的性质:矩形的四个角都是直角.几何语言:∵ABCD是矩形,∴∠A=∠B=∠C=∠D=90°.矩形中的折叠问题
矩形的性质
边:对边平行且相等
角:四个角都是直角
对角线:对角线互相平分且相等
矩 形
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(1)图中全等的图形有哪些
(2)有(1)可以得到的,
相等的线段有哪些?
相等的角有哪些?
(3)图中还有哪些特殊的三角形?
(直角三角形除外)
(4)当AB=4,BC=8时,
重合部分的面积是多少?
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(1)图中全等的图形有哪些
△ABC≌ADC≌△AFC
△ABE≌△CFE
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(2)有(1)可以得到的,
相等的线段有哪些?
相等的角有哪些?
CD=CF=AB,AD=AF=BC,
AE=EC, BE=EF
∠D=∠F=∠B=90°
∠DAC=∠FAC,∠ACD=∠ACF,
∠BAE=∠ECF,∠BEA=∠FEC
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(3)图中还有哪些特殊的三角形?
(直角三角形除外)
答:△AEC为等腰三角形
证明:∵矩形ABCD,
∴AD∥BC
∴∠DAC=∠ACE,
又∵∠DAC=∠FAC
∴∠ACE=∠FEC,
∴AE=EC
即△AEC为等腰三角形
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(4)当AB=4,BC=8时,
重合部分的面积是多少?
解;由题意可得,重合部分为△AEC
设EC=X,则AE=EC=X,
∵BC=8,
∴BE=8-X
又∵AB=4,
在Rt△ABE中,有勾股定理可得,
解得:X=5
∴EC=5
∴S△AEC=5×4÷2
=10
巩固练习
如图,已知矩形ABCD,将其沿对角线BD折叠,点C落在点E处,BE交AD于点F.
(1) 若∠ADE=20°,求∠FBD
(2) 若AB=4,BC=8,求AF
,
解:(1)∵矩形ABCD中,∠C=90°,
又∵翻折,
∴∠E=∠C=90°,
∵∠ADE=20°,
∴∠EFD=70°
. ∵AD∥BC,
∴∠FDB=∠DBC ,
又∵∠FBD=∠DBC,
∴ ∠ FBD=∠FDB,
∴∠FBD=70°÷2=35°.
(2)∵∠FBD=∠FDB,∴FB=FD,
设AF为x,则FD=FB= 8-x,
在△ABF中,∠A=90°,
因此 , 解得 ,
∴AF=3.
B
C
D
E
F
A
课堂小结
1.折叠的过程,实质上就是一个轴对称的变换,折痕就是对称轴,变换前后的两个图形全等。
2.在矩形的折叠问题中,求线段长时,常设未知数,找到相应的直角三角形,用勾股定理建立方程,利用方程思想解决问题。
感 谢 聆 听
18.2.1 矩形
(1)矩形的性质和矩形性质的应用
(2)矩形中的折叠问题
人教版数学八级下册
矩形的性质和矩形性质的应用
导入观察下面图形,长方形在生活中无处不在.你还能举出其他的例子吗?思考长方形跟我们前面学行四边形有什么关系? 利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察。
矩形
观察在不断地改变图形的一个内角的大小过程中,图形的形状是否发生了变化?思考当这个角变成直角时,那么得到的是一个什么图形?
知识讲解定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.平行四边形矩形有一个角是直角矩形是特殊的平行四边形.平行四边形不一定是矩形.思考因为矩形是平行四边形,所以它具有平行四边形的边、角、对角线的所有性质,又由于矩形有一个角为直角,所以矩形是否具有一些特殊的性质呢?这也是矩形的一种判定方法。活动与探究(温馨提示:规范操作、注意安全)
知识讲解
难点突破
猜想 矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,∠B=90°.
求证: ∠B=∠C=∠D=∠A=90°.
A
B
C
D
证明:∵四边形ABCD是矩形,
∴∠B=∠D,∠C=∠A, AB∥DC.
∴∠B+∠C=180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B=∠C=∠D=∠A =90°.
知识讲解矩形的四个角都是直角.矩形除了具有平行四边形所有性质,还具有特殊性质:几何语言:∵ 四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°(矩形的四个角都是直角).课堂练习难点巩固例如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE,垂足为F.求证:DF=DC.ACDEF证明:连接DE.∵AD=AE,∴∠AED=∠ADE.∵四边形ABCD是矩形,∴AD∥BC,∠C=90°.∴∠ADE=∠DEC,∴∠DEC=∠AED.又∵DF⊥AE, ∴∠DFE=∠C=90°.B又∵DE=DE,∴△DFE≌△DCE,∴DF=DC.课堂小结定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.矩形是特殊的平行四边形平行四边形不一定是矩形.矩形的性质:矩形的四个角都是直角.几何语言:∵ABCD是矩形,∴∠A=∠B=∠C=∠D=90°.矩形中的折叠问题
矩形的性质
边:对边平行且相等
角:四个角都是直角
对角线:对角线互相平分且相等
矩 形
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(1)图中全等的图形有哪些
(2)有(1)可以得到的,
相等的线段有哪些?
相等的角有哪些?
(3)图中还有哪些特殊的三角形?
(直角三角形除外)
(4)当AB=4,BC=8时,
重合部分的面积是多少?
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(1)图中全等的图形有哪些
△ABC≌ADC≌△AFC
△ABE≌△CFE
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(2)有(1)可以得到的,
相等的线段有哪些?
相等的角有哪些?
CD=CF=AB,AD=AF=BC,
AE=EC, BE=EF
∠D=∠F=∠B=90°
∠DAC=∠FAC,∠ACD=∠ACF,
∠BAE=∠ECF,∠BEA=∠FEC
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(3)图中还有哪些特殊的三角形?
(直角三角形除外)
答:△AEC为等腰三角形
证明:∵矩形ABCD,
∴AD∥BC
∴∠DAC=∠ACE,
又∵∠DAC=∠FAC
∴∠ACE=∠FEC,
∴AE=EC
即△AEC为等腰三角形
【折叠问题】
如图所示,在矩形ABCD中,把△ADC沿AC折叠到△AFC,AF与BC交于点E.
(4)当AB=4,BC=8时,
重合部分的面积是多少?
解;由题意可得,重合部分为△AEC
设EC=X,则AE=EC=X,
∵BC=8,
∴BE=8-X
又∵AB=4,
在Rt△ABE中,有勾股定理可得,
解得:X=5
∴EC=5
∴S△AEC=5×4÷2
=10
巩固练习
如图,已知矩形ABCD,将其沿对角线BD折叠,点C落在点E处,BE交AD于点F.
(1) 若∠ADE=20°,求∠FBD
(2) 若AB=4,BC=8,求AF
,
解:(1)∵矩形ABCD中,∠C=90°,
又∵翻折,
∴∠E=∠C=90°,
∵∠ADE=20°,
∴∠EFD=70°
. ∵AD∥BC,
∴∠FDB=∠DBC ,
又∵∠FBD=∠DBC,
∴ ∠ FBD=∠FDB,
∴∠FBD=70°÷2=35°.
(2)∵∠FBD=∠FDB,∴FB=FD,
设AF为x,则FD=FB= 8-x,
在△ABF中,∠A=90°,
因此 , 解得 ,
∴AF=3.
B
C
D
E
F
A
课堂小结
1.折叠的过程,实质上就是一个轴对称的变换,折痕就是对称轴,变换前后的两个图形全等。
2.在矩形的折叠问题中,求线段长时,常设未知数,找到相应的直角三角形,用勾股定理建立方程,利用方程思想解决问题。
感 谢 聆 听
