2021-2022学年人教版数学七年级下册8.2 加减消元法 解二元一次方程组的强化训练 课件(25张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册8.2 加减消元法 解二元一次方程组的强化训练 课件(25张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 11:35:32 | ||
图片预览






文档简介
(共25张PPT)
8.2 消元——解二元一次方程组
(1)加减消元法
(2)解二元一次方程组的强化训练
人教版数学七级下册
加减消元法
1.会用加减消元法解二元一次方程组,并掌握加减法解二元一次方程组的步骤.
2.经历探索加减消元法解二元一次方程组的过程,领会消元法所体现的思想方法.
学习目标
消元: 二元
一元
回代
求解
代入
变形
2.用代入法解方程的步骤是什么?
1.解二元一次方程组的基本思想是什么?
写解
用一个未知数的代数式
表示另一个未知数
一、复习回顾
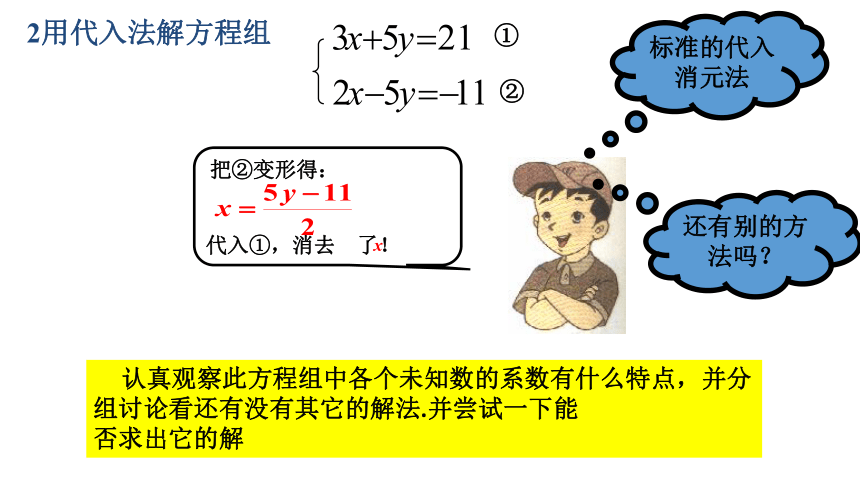
2用代入法解方程组
代入①,消去 了!
把②变形得:
标准的代入消元法
②
①
认真观察此方程组中各个未知数的系数有什么特点,并分组讨论看还有没有其它的解法.并尝试一下能
否求出它的解
还有别的方法吗?
2x -3y=-2 ①
5x+3y=16 ②
变式训练
2x-3y=-2 ①
5x-3y=16 ②
归纳:
系数相反就用加
系数相同就用减
归纳定义:
从上面两个方程组的解法看出,当二元一次方程组中两个方程中同一未知数的系数 相反 或 相等时,把这两个方程组的两边分别 相加 或 相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法。
观察方程组:
9 x - 2 y =15 ①
3 x +4 y =10 ②
①×2 得: 18x-4y=30 ③ ② ×3 得: 9x+12y=30 ③
③+②得: 21x=40 ③ - ①得: 14y=15
方程两边能乘以同一个数的依据是什么?
你发现了什么特点?怎样消元?
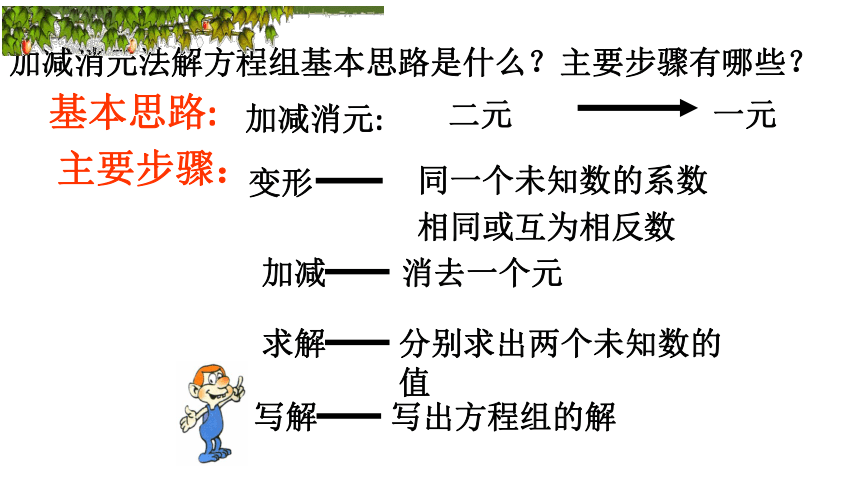
基本思路:
主要步骤:
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
加减消元法解方程组基本思路是什么?主要步骤有哪些?
变形
同一个未知数的系数
相同或互为相反数
写解
写出方程组的解
5x+3y=21 ①
3x+2y=13 ②
例
解:① ×2 得:10x+6y=42 ③ 解:① ×3 得: 15x+9y=63 ③
② ×3 得: 9x+6y=39 ④ ② ×5 得:15x+10y=65④
③ - ④得: x=3 ④ - ③得: y=2
把 x=3 代入②得: 把 y=2 代入②得:
9+2y=13 3 x +4=13
y=2 x =3
∴ x=3 ∴ x =3
y=2 y=2
①
②
下列方程组用什么方法消元比较简便?
2x-7y=16 ①
3x+6y=10 ②
x+3y=17 ①
2x-3y=6 ②
y=2x ①
6x-5y=17 ②
2、若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
1、加减消元法:两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,
小结:学习了本节课你有哪些收获?
2、加减消元法解方程组的主要步骤:
加减
消去一个元
求解
分别求出两个未知数的值
变形
同一个未知数的系数相同或互为相反数
写解
写出方程组的解
解二元一次方程组的强化训练
回顾:
1、解二元一次方程组的基本思路是什么?
解二元一次方程组的基本思路是消元.
2、二元一次方程组有哪两种解法?
代入消元法和加减消元法.
3、解二元一次方程组中“代入”与“加减”的目的是什么?
消去两个未知数中的一个.
解法1:
代入
消元法
解法2:
加减
消元法
解法3:
整体思想
练习1、用带入消元法解方程组
练习2、用加减消元法解方程组
解:
令m=2x+3y,n=2x-3y,则方程组转化为:
换元法解放程组
巩固提升
5
巩固提升
2、某步行街摆放若干盆甲、乙、丙三种造型得盆景。甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成。这些盆景一共用了2900朵红花,3750朵紫花,则黄花一共用 朵。
4380
归纳小结
1、解一元二次方程组的基本方法有代入消元法和加减消元法。
2、解二元一次方程组的思想是“消元思想”。
3、二元一次方程组的特殊解法:换元法、整体代入法、参数法等。
感 谢 聆 听
8.2 消元——解二元一次方程组
(1)加减消元法
(2)解二元一次方程组的强化训练
人教版数学七级下册
加减消元法
1.会用加减消元法解二元一次方程组,并掌握加减法解二元一次方程组的步骤.
2.经历探索加减消元法解二元一次方程组的过程,领会消元法所体现的思想方法.
学习目标
消元: 二元
一元
回代
求解
代入
变形
2.用代入法解方程的步骤是什么?
1.解二元一次方程组的基本思想是什么?
写解
用一个未知数的代数式
表示另一个未知数
一、复习回顾
2用代入法解方程组
代入①,消去 了!
把②变形得:
标准的代入消元法
②
①
认真观察此方程组中各个未知数的系数有什么特点,并分组讨论看还有没有其它的解法.并尝试一下能
否求出它的解
还有别的方法吗?
2x -3y=-2 ①
5x+3y=16 ②
变式训练
2x-3y=-2 ①
5x-3y=16 ②
归纳:
系数相反就用加
系数相同就用减
归纳定义:
从上面两个方程组的解法看出,当二元一次方程组中两个方程中同一未知数的系数 相反 或 相等时,把这两个方程组的两边分别 相加 或 相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法。
观察方程组:
9 x - 2 y =15 ①
3 x +4 y =10 ②
①×2 得: 18x-4y=30 ③ ② ×3 得: 9x+12y=30 ③
③+②得: 21x=40 ③ - ①得: 14y=15
方程两边能乘以同一个数的依据是什么?
你发现了什么特点?怎样消元?
基本思路:
主要步骤:
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
加减消元法解方程组基本思路是什么?主要步骤有哪些?
变形
同一个未知数的系数
相同或互为相反数
写解
写出方程组的解
5x+3y=21 ①
3x+2y=13 ②
例
解:① ×2 得:10x+6y=42 ③ 解:① ×3 得: 15x+9y=63 ③
② ×3 得: 9x+6y=39 ④ ② ×5 得:15x+10y=65④
③ - ④得: x=3 ④ - ③得: y=2
把 x=3 代入②得: 把 y=2 代入②得:
9+2y=13 3 x +4=13
y=2 x =3
∴ x=3 ∴ x =3
y=2 y=2
①
②
下列方程组用什么方法消元比较简便?
2x-7y=16 ①
3x+6y=10 ②
x+3y=17 ①
2x-3y=6 ②
y=2x ①
6x-5y=17 ②
2、若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
1、加减消元法:两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,
小结:学习了本节课你有哪些收获?
2、加减消元法解方程组的主要步骤:
加减
消去一个元
求解
分别求出两个未知数的值
变形
同一个未知数的系数相同或互为相反数
写解
写出方程组的解
解二元一次方程组的强化训练
回顾:
1、解二元一次方程组的基本思路是什么?
解二元一次方程组的基本思路是消元.
2、二元一次方程组有哪两种解法?
代入消元法和加减消元法.
3、解二元一次方程组中“代入”与“加减”的目的是什么?
消去两个未知数中的一个.
解法1:
代入
消元法
解法2:
加减
消元法
解法3:
整体思想
练习1、用带入消元法解方程组
练习2、用加减消元法解方程组
解:
令m=2x+3y,n=2x-3y,则方程组转化为:
换元法解放程组
巩固提升
5
巩固提升
2、某步行街摆放若干盆甲、乙、丙三种造型得盆景。甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成。这些盆景一共用了2900朵红花,3750朵紫花,则黄花一共用 朵。
4380
归纳小结
1、解一元二次方程组的基本方法有代入消元法和加减消元法。
2、解二元一次方程组的思想是“消元思想”。
3、二元一次方程组的特殊解法:换元法、整体代入法、参数法等。
感 谢 聆 听
