第一章 碰撞与动量守恒 综合训练(Word版含解析)
文档属性
| 名称 | 第一章 碰撞与动量守恒 综合训练(Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 261.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-23 19:43:29 | ||
图片预览




文档简介
第1章碰撞与动量守恒
一、选择题(共15题)
1.如图,在光滑水平面上,轨道ABCD的质量M =0.4 kg,其中AB段是半径R=0.4 m的光滑弧,在B点与水平轨道BD相切,水平轨道的BC段粗糙,动摩擦因数μ=0.4,长L=3.5 m,C点右侧的轨道光滑,轨道的右端连接一轻质弹簧。 现有一质量m=0.1kg的小物体在A点正上方高为H=3.6m处由静止自由落下,恰沿A点切线滑入圆弧轨道,重力加速度g=10 m/s2。下列说法正确的是( )
A.小物体和轨道组成的系统在全过程中动量守恒
B.小物体第一次返回到A点时的速度为m/s
C.小物体第一次返回到A点时的速度为0
D.轨道M在水平面上运动的最大速率为2.0 m/s.
2.如图所示,大气球质量为100kg,载有质量为50kg的人(可以把人看做质点),静止在空气中距地面20m高的地方,气球下方悬一根质量可忽略不计的绳子,此人想从气球上沿绳慢慢下滑至地面,为了安全到达地面,则这绳长至少应为( )
A.20m B.30m C.40m D.50m
3.如图所示,甲木块的质量为 ,以速度 沿光滑水平地面向前运动,正前方有一静止的、质量为 的乙木块,乙上连有一轻质弹簧,甲木块与弹簧接触后( )
A.甲木块的动量守恒
B.乙木块的动量守恒
C.甲、乙两木块所组成的系统的动量守恒
D.甲、乙两木块所组成的系统的动能守恒
4.在光滑水平直路上停着一辆较长的木板车,车的左端站立一个大人,车的右端站立一个小孩.如果大人向右走,小孩(质量比大人小)向左走.他们的速度大小相同,则在他们走动过程中( )
A.车可能向右运动 B.车一定向左运动
C.车可能保持静止 D.无法确定
5.如图所示,A、B两物体的质量比mA:mB=4:3,它们原来静止在足够长的平板车C上,A、B间有一根被压缩了的弹簧,地面光滑。当弹簧突然释放后,且已知A、B组成的系统动量守恒。则有
A.A,B与C的动摩擦因数相等 B.A,B与C的动摩擦因数不相等
C.最终稳定时小车向右运动 D.A,B,C系统动量不守恒
6.关于物体的动量和冲量,下列说法不正确的是( )
A.物体所受合外力的冲量越大,它的动量也越大
B.物体所受合外力的冲量不为零,它的动量一定要改变
C.物体的动量增量的方向,就是它所受合外力的冲量的方向
D.物体所受合外力越大,它的动量变化就越快
7.如图所示,有一子弹穿过三块静止放置在光滑水平面上的相互接触质量分别为 m、2m、3m 的木块 A、B、C,设子弹穿过木块 A、B 、C 的时间分别为 t1、t2、t3,木块对子弹的阻力恒为 f,则子弹穿过三木块后,木块 A 的速度大小是( )
A. B.
C. D.
8.如图所示,站在车上的人,用锤子连续敲打小车。初始时,人、车、锤都静止。假设水平地面光滑,关于这一物理过程,下列说法正确的是( )
A.连续敲打可使小车持续向右运动
B.人、车和锤组成的系统机械能守恒
C.当锤子速度方向竖直向下时,人和车水平方向的总动量为零
D.人、车和锤组成的系统动量守恒
9.下列说法中正确的是( )
A.由 可知物体动量的变化率等于它受的合外力
B.冲量反映了力的作用对时间的累积效应,是一个标量
C.易碎品运输时要用柔软材料包装是为了减小冲量
D.玻璃杯掉在水泥地上易碎,是因为受到的冲量太大
10.如图,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触,现将摆球a向左拉开一小角度后释放。若两球的碰撞是弹性的,下列判断正确的是( )
A.第一次碰撞后的瞬间,两球的动能大小相等
B.第一次碰撞后的瞬间,两球的动量大小相等
C.第一次碰撞后的瞬间,两球的速度大小相等
D.第一次碰撞后,两球的最大摆角不相同
11.物体在恒定的合外力F作用下做直线运动,在时间Δt1内速度由0增大到v,在时间Δt2内速度由v增大到2v.设F在Δt1内做的功是W1,冲量是I1;在Δt2内做的功是W2,冲量是I2.那么( )
A.I2 = I1 W2 > W1 B.I2 < I1 W2 < W1
C.I2 > I1 W2 > W1 D.I2 = I1 W2 < W1
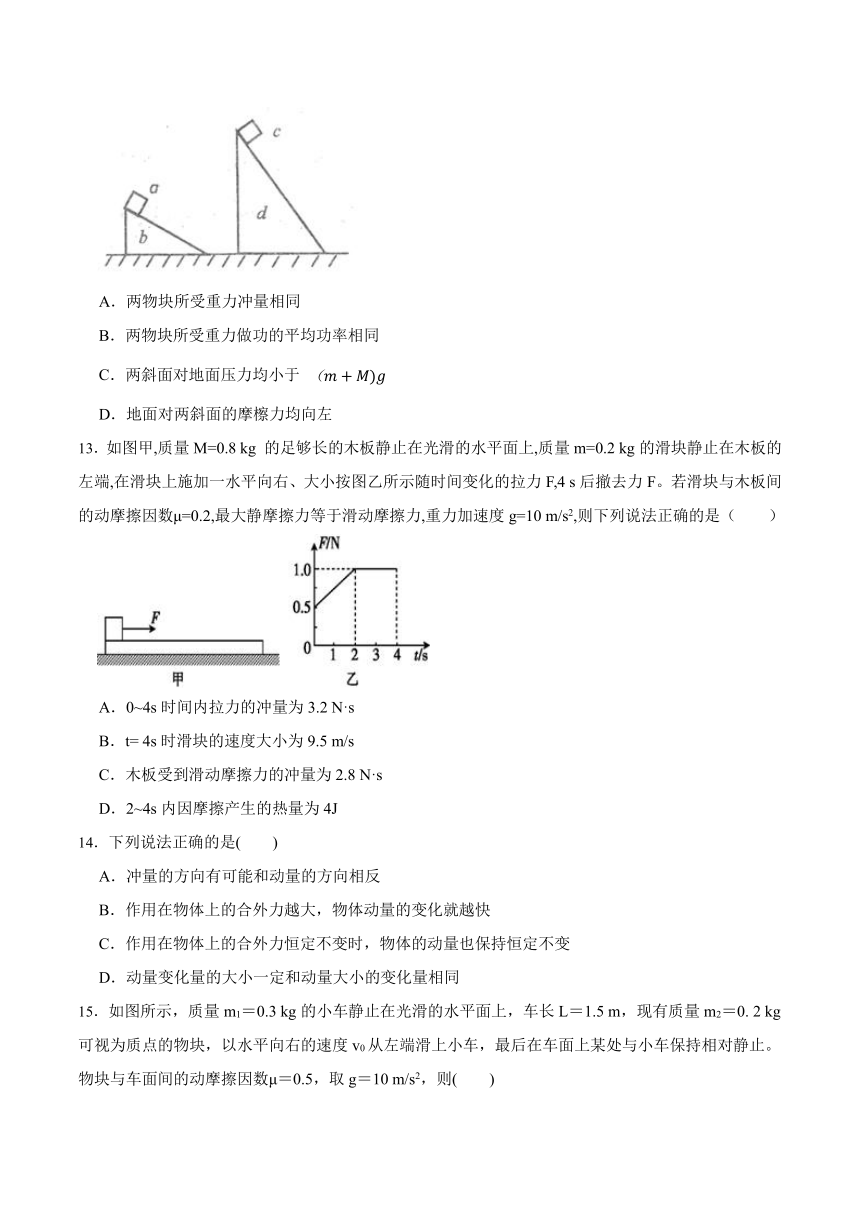
12.如图所示,质量均为M的b、d两个光滑斜面静止于水平面上,底边长度相等,b斜面倾角为30°,d斜面倾角为60°.质量均为m的小物块a和c分别从两个斜面顶端由静止自甶滑下,下滑过程中两斜面始终静止.小物块到达斜面底端的过程中,下列说法正确的是( )
A.两物块所受重力冲量相同
B.两物块所受重力做功的平均功率相同
C.两斜面对地面压力均小于
D.地面对两斜面的摩檫力均向左
13.如图甲,质量M=0.8 kg 的足够长的木板静止在光滑的水平面上,质量m=0.2 kg的滑块静止在木板的左端,在滑块上施加一水平向右、大小按图乙所示随时间变化的拉力F,4 s后撤去力F。若滑块与木板间的动摩擦因数μ=0.2,最大静摩擦力等于滑动摩擦力,重力加速度g=10 m/s2,则下列说法正确的是( )
A.0~4s时间内拉力的冲量为3.2 N·s
B.t= 4s时滑块的速度大小为9.5 m/s
C.木板受到滑动摩擦力的冲量为2.8 N·s
D.2~4s内因摩擦产生的热量为4J
14.下列说法正确的是( )
A.冲量的方向有可能和动量的方向相反
B.作用在物体上的合外力越大,物体动量的变化就越快
C.作用在物体上的合外力恒定不变时,物体的动量也保持恒定不变
D.动量变化量的大小一定和动量大小的变化量相同
15.如图所示,质量m1=0.3 kg的小车静止在光滑的水平面上,车长L=1.5 m,现有质量m2=0. 2 kg可视为质点的物块,以水平向右的速度v0从左端滑上小车,最后在车面上某处与小车保持相对静止。物块与车面间的动摩擦因数μ=0.5,取g=10 m/s2,则( )
A.物块滑上小车后,滑块和小车构成的系统动量守恒。
B.物块滑上小车后,滑块和小车构成的系统机械能守恒。
C.若v0=2m/s,则物块在车面上滑行的时间为0.24s;
D.若要保证物块不从小车右端滑出,则v0不得大于5m/s
二、填空题
16.一个物体静置于光滑水平面上,外面扣一质量为M的盒子,如图甲所示。现给盒子一初速度v0,此后,盒子运动的v-t图象呈周期性变化,如图乙所示,据此可知盒内物体的质量是 。
17.某同学用图所示的 “碰撞实验装置”研究直径相同的两个小球在轨道水平部分碰撞前后的动量关系。
①在实验中小球速度不易测量,可通过仅测量 解决这一问题。
A.小球做平抛运动的时间
B.小球做平抛运动的水平距离
C.小球做平抛运动的初始高度
D.小球释放时的高度
②图中PQ是斜槽,QR为水平槽,R为水平槽末端。利用铅垂线在记录纸上确定R的投影点O。实验时先使A球从斜槽上G处由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹;此后,再把B球放在R处,将A球再从G处由静止释放,与B球碰撞后在记录纸上分别留下A、B两球落点痕迹。由测量可知,碰撞前A球做平抛运动的水平距离为x0;碰撞后,A、B两球做平抛运动的水平距离分别为x1、x2。用天平称量A、B两球的质量分别为mA、mB。若两球相碰前后的动量守恒,其表达式可表示为 (用题目给出的物理量符号表示)。
18.如图甲所示,在探究碰撞中的不变量实验时,长木板光滑且处于水平,小车A的前端粘有橡皮泥,用手推动一下小车A,放手后小车A做匀速运动,然后与原来諍止在前方的小车B相碰并粘合在一起,之后继续匀速运动,在小车A后连着纸带,打点计时器电源周期为0.02s。
①若获得纸带如图乙所示,a为运动的起始点,从a点开始,每5个点取一个计数点,其中a、b、c、d、e都为计数点,并测得相邻计数点间距(已标在图上),则应选 段来计算A的碰前速度,应选 段来计算A和B碰后的共同速度(填ab、bc、cd或de)。
②已测得小车A(含橡皮泥)的质量mA=0.30kg,小车B(含撞针)的质量为mB=0.20kg,由以上测量结果可得碰前系统总动量为 kg·m/s,碰后系统总动量为 kg·m/s。(结果均保留三位有效数字)
19.光滑水平面上两小球a、b用不可伸长的松弛细绳相连。开始时a球静止,b球以一定速度运动直至绳被拉紧,然后两球一起运动,在此过程中两球的总动量 (填“守恒”或“不守恒”);机械能 (填“守恒”或“不守恒”)。
三、综合题
20.如图所示,质量M= 1kg的木板静止在足够长的固定光滑斜面上,斜面倾角 ,木板下端上表面恰与整直面内的光滑圆弧轨道BCD在D点相切,圆弧半径为R=11m,半径OB与竖直方向夹角为a=53°。一质量m=2kg(可视为质点)的小滑块以v0=6m/s的初速度从左侧水平桌面飞出,并恰好从B点沿切线进入圆弧轨道。已知滑块和木板之间的动摩擦因数μ=0.5,滑块不会从木板上端滑出,重力加速度g= 10m/s2,求∶
(1)滑块经过圆弧轨道上D点,圆弧轨道对它的弹力;
(2)木板上升过程中因摩擦产生的热量Q;
(3)木板下端第一次返回D点时,木板在斜面上运动的时间t。
21.如图所示,在倾角为30°的光滑斜面上放置一质量为m的物块B,B的下端连接一轻质弹簧,弹簧下端与挡板相连接,B平衡时,弹簧的压缩量为x0,O点为弹簧的原长位置。在斜面顶端另有一质量也为m的物块A,距物块B为3x0,现让A从静止开始沿斜面下滑,A与B相碰后立即一起沿斜面向下运动,但不粘连,它们到达最低点后又一起向上运动,并恰好回到O点(A、B均视为质点)。试求:
(1)A、B相碰后瞬间的共同速度的大小;
(2)A、B相碰前弹簧具有的弹性势能;
(3)若在斜面顶端再连接一光滑的半径R=x0的半圆轨道PQ,圆弧轨道与斜面相切于最高点P,现让物块A以初速度v从P点沿斜面下滑,与B碰后返回到P点还具有向上的速度,则v为多大时物块A恰能通过圆弧轨道的最高点?
22.如图所示,光滑的四分之一圆弧与光滑水平轨道在最低平滑连接。现有一质量为m的小球P沿光滑的四分之一圆弧上由静止开始下滑,与一质量为km(k>0,未知)的静止在光滑水平地面上的等大的小球Q发生正碰撞。设碰撞是弹性的,且一切摩擦不计。
(1)为使二者能且只能发生一次碰撞,则k的值应满足什么条件?
(2)为使二者能且只能发生两次碰撞,则k的值应满足什么条件?
23.如图甲所示的一种离子推进器,由离子源、间距为的平行金属板、和边长为的立方体构成,其中、正中间各有一个小孔且两小孔正对,工作原理简化图如图乙所示。氙离子从腔室中飘移过栅电极的速度大小可忽略不计,在栅电极、之间的匀强电场中加速,并从栅电极喷出,在加速氙离子(质量为、电荷量为)的过程中飞船获得推力,不计氙离子间的相互作用及重力影响。
(1)若该离子推进器固定在地面上实验时,在的右侧立方体间加垂直向里的匀强磁场,从电极中央射入的离子加速后经电板的中央点进入磁场,恰好打在立方体棱边的中点上。求、之间的电压与磁感应强度的关系式。
(2)若宇宙飞船处于悬浮状态(离子推进器停止工作),宇航员在飞船内从静止经多次往复运动后回到原位置不动,判断飞船最终是否偏离原位置?若偏离,请计算相对原位置的距离;若不偏离,请说明理由。
(3)若撤去离子推进器中的磁场,悬浮状态下的推进器在某段时间内喷射的个氙离子以速度通过栅极,该过程中离子和飞船获得的总动能占发动机提供能量的倍,飞船的总质量及获得的动力保持不变,已知发动机总功率为,求动力大小。
答案部分
1.D
【解答】A.小物体和轨道组成的系统全过程中只在水平方向上合外力为零,故全过程中水平方向动量守恒,A不符合题意;
BC.由题意分析可知,小物体第一次沿轨道返回到A点时小物体与轨道在水平方向的分速度相同,设为,假设此时小物体在竖直方向的分速度为,则对小物体和轨道组成的系统,由水平方向动量守恒得
由能量守恒得
解得
即小物体第一次返回到A点时的速度为
BC不符合题意;
D.由题意分析可知,当小物体沿运动到圆弧最低点B时轨道的速率最大,设为,假设此时小物体的速度大小为,则小物体和轨道组成的系统水平方向动量守恒,以初速度的方向为正方向,由动量守恒定律可得
由机械能守恒得
解得
D符合题意。
故答案为:D。
2.B
【解答】人与气球组成的系统动量守恒,设人的速度v1,气球的速度v2,设运动时间为t,以人与气球组成的系统为研究对象,以向下为正方向,由动量守恒得:m1v1-m2v2=0,则 ,解得:
则绳子长度:L=s球+s人=10m+20m=30m
即绳子至少长30m长。
故答案为:B
3.C
【解答】甲木块与弹簧接触后,由于弹簧弹力的作用,甲、乙的动量要发生变化,即甲、乙两物体的动量均不守恒;但对于甲、乙所组成的系统因所受合力的冲量为零,故动量守恒,AB不符合题意,C符合题意;甲、乙两木块所组成系统的动能,一部分转化为弹簧的势能,故系统动能不守恒,D不符合题意.
故答案为:C
4.B
【解答】系统动量守恒,且总动量为零,由于大人质量大于小孩,速度相同,因此大人与小孩的总动量向右,为满足动量守恒,车一定向左运动,ACD不符合题意,B符合题意.
故答案为:B.
5.B
【解答】AB.A、B组成的系统动量守恒,则AB两物体所受的摩擦力应该大小相等方向相反,系统所受合外力才为0,因为AB质量不相等所以动摩擦因数不相等,A不符合题意,B符合题意。
CD.ABC三物体所组成的系统动所受合外力为0,动量守恒。最终稳定时,三个物体应该都处于静止状态,CD不符合题意。
故答案为:B。
6.A
【解答】A.物体所受合外力的冲量越大,它的动量变化量越大,并不是动量越大,A错误,符合题意;
B.物体所受合外力的冲量不为零,它的动量一定要改变,B正确,不符合题意;
C.物体的动量增量的方向,就是它所受合外力的冲量的方向,C正确,不符合题意;
D.根据动量定理和牛顿第二定律可知,物体所受合外力等于动量的变化率,所以合外力越大,动量变化就越快,D正确,不符合题意。
故答案为:A。
7.C
【解答】A与B分离时三者的速度是相等的,分离后,A的速度不变,在分离前子弹对系统的作用力使A、B与C的速度增大,由动量定理得
所以
故答案为:C。
8.C
【解答】A.人、车和锤看做一个系统处在光滑水平地面上,水平方向所受合外力为零,故水平方向动量守恒,总动量始终为零,当大锤有相对大地向左的速度时,车有向右的速度,当大锤有相对大地向右的速度时,车有向左的速度,故车来回运动,A不符合题意;B.大锤击打小车时,发生的不是完全弹性碰撞,系统机械能有损耗,B不符合题意;C.大锤的速度竖直向下时,没有水平方向的速度,因为水平方向总动量恒为零,故人和车的总动量也为零,C符合题意;D.人、车和锤水平方向动量守恒,因为大锤会有竖直方向的加速度,故竖直方向合外力不为零,竖直动量不守恒,系统总动量不守恒,D不符合题意。
故答案为:C
9.A
【解答】A.由 可知物体动量的变化率等于它受的合外力,所以A符合题意;
B.冲量反映了力的作用对时间的累积效应,是一个矢量,所以B不符合题意;
C.易碎品运输时要用柔软材料包装是为了延长作用时间,减小冲击力,所以C不符合题意;
D.玻璃杯掉在水泥地上易碎,是因为作用时间短,受到的冲击力太大,所以D不符合题意;
故答案为:A。
10.C
【解答】两球在碰撞前后,水平方向不受外力,故水平方向两球组成的系统动量守恒,由动量守恒定律有:mv0=mv1+3mv2,两球碰撞是弹性的,故机械能守恒,即: mv02= mv12+ 3mv22,解两式得:v1=- ,v2= ,可见第一次碰撞后的瞬间,两球的速度大小相等;因两球质量不相等,故两球碰后的动量大小不相等,方向相反,动能也不相等,AB不符合题意,C符合题意;两球碰后上摆过程,机械能守恒,故上升的最大高度相等,另摆长相等,故两球碰后的最大摆角相同,D不符合题意。 故答案为:C
11.A
【解答】根据动能定理得:
则W1<W2。
根据动量定理得,I1=mv-0=mv
I2=2mv-mv=mv
知I1=I2.
故答案为:A。
12.A,C
【解答】设斜面的倾角为 时下滑的时间为 ,设斜面底端长度为 ,则斜面长为 ,根据牛顿第二定律可得加速度为: ,根据运动学公式可得: ,解得: ,由于两个斜面的倾角分别为 和 ,则可知 、 沿斜面下滑的时间相等;
A、两物块所受重力冲量 相同, A符合题意;
B、重力做功的平均功率为 ,由于 不同,所以两物块所受重力做功的平均功率不相同, B不符合题意;
C、小物块加速下滑过程中在竖直方向的加速度方向向下,处于失重状态,以整体为研究对象,两斜面对地面压力均小于 ,C符合题意;
D、以整体为研究对象,小物块水平方向的加速度方向都向右,而斜面的加速度为零,根据 可知地面对两斜面的摩擦力均向右,D不符合题意.
故答案为:AC
13.B,C,D
【解答】A.冲量的定义式: ,所以F-t图像面积代表冲量,所以0-4 s时间内拉力的冲量为
A不符合题意;
B.木块相对木板滑动时:对木板:
对木块:
联立解得: ,
所以0时刻,即相对滑动,对滑块:
解得4s时滑块速度大小: B符合题意;
C.4s时,木板的速度
撤去外力后,木板加速,滑块减速,直到共速,根据动量守恒:
解得: ,
对木板根据动量定理可得:
C符合题意;
D.0-2s内,对m:
解得:
对M
解得v2=1m/s
2-4s内:对m
;
对M
所以
D符合题意。
故答案为:BCD
14.A,B
【解答】冲量的方向与动量变化的方向相同,有可能和动量的方向相反,A符合题意;根据动量定理可知,合外力等于动量的变化率,则作用在物体上的合外力越大,物体动量的变化就越快,B符合题意;作用在物体上的合外力恒定不变时,合外力的冲量不为零,则物体的动量要发生变化,C不符合题意;当物体做曲线运动时,动量变化量的大小和动量大小的变化量不相同,D不符合题意.
故答案为:AB
15.A,C,D
【解答】由于地面光滑,所以物块和小车构成的系统动量守恒,A符合题意;由于物块和小车之间有摩擦力,所以系统机械能不守恒,B不符合题意;设物块与小车的共同速度为v,以水平向右的方向为正方向,根据动量守恒定律有 ,设物块与车面间的滑动摩擦力为 ,则 对物块应用动量定理有 ,解得 ,代入数据得 ,C符合题意;要使物块恰好不从车面上滑出,须物块到车面最右端时与小车有共同的速度,设其为v′,则 ,由功能关系有 ,代入数据解得 ,D符合题意;
故答案为:ACD
16.M
【解答】设物体的质量为m,t0时刻受盒子碰撞获得速度v,根据动量守恒定律得:Mv0=mv①
3t0时刻物体与盒子右壁碰撞使盒子速度又变为v0,说明物体速度变为零,且碰撞是弹性碰撞,由机械能守恒有: M = mv2②
联立①②解得m=M
17.B; ;
【解答】(1)因为平抛运动的速度等于射程与落地时间的比值,而当高度一定时,落地时间一定,所以可以测量射程代替速度,故答案为:B;(2) 要验证动量守恒定律定律,即验证: ,小球离开轨道后做平抛运动,它们抛出点的高度相等,在空中的运动时间t相等,上式两边同时乘以t得, ,若两球相碰前后的动量守恒,得:
18.bc;de;1.04;1.03
【解答】①推动小车由静止开始运动,故小车有个加速过程,在碰撞前做匀速直线运动,即在相同的时间内通过的位移相同,Bc段为匀速运动的阶段,故答案为:bc计算碰前的速度;碰撞过程是一个变速运动的过程,而A和B碰后的共同运动时做匀速直线运动,故在相同的时间内通过相同的位移,故应选de段来计算碰后共同的速度;②A碰前的速度
碰后共同速度
碰前系统总动量
碰后系统总动量
19.守恒;不守恒
【解答】将a b组成系统,对系统受力分析知合外力为零,故系统动量守恒;而在此过程拉力对b做负功,机械能不守恒。
20.(1)由几何关系知滑块经过B点时
滑块在B到D的过程由动能定理得
解得
滑块在D点由牛顿第二定律
解得
方向垂直与斜面向上;
(2)滑块冲上木板后,设经过 时间达到共同速度 ,则在这个过程中
取沿斜面向上为正方向,对滑块有
对木板有
解得
此过程中,滑块的位移
木板的位移
此后过程中滑块与木板保持相对静止,所以上升过程中摩擦生热为
(3)设木板下端返回D点时速度为 ,共速后对整体有
解得
取沿斜面向下为正方向有
解得
所以木板在斜面上运动的时间为
21.(1)解:A与B碰撞前后,设A的速度分别是 和
A下滑过程中,机械能守恒,有:
解得: ①
又因A与B碰撞过程中,动量守恒,有:
②
联立①②得
(2)解:碰后,A、B和弹簧组成的系统在运动过程中,机械能守恒。
则有:
又由(1)得
代入解得: ③
(3)解:设物块A在最高点C的速度是
物块A恰能通过圆弧轨道的最高点C点时,重力提供向心力,得:
C点相对于O点的高度,如图所示:
物块从O到C的过程中机械能守恒,得:
设A与B碰撞后共同的速度为 ,碰撞前A的速度为 ,
物块A从P到与B碰撞前的过程中机械能守恒,得:
A与B碰撞的过程中动量守恒,得:
A与B碰撞结束后到O的过程中机械能守恒,得: ⑩
由于A与B不粘连,到达O点时,滑块B开始受到弹簧的拉力,A与B分离。
综合上述式子解得:
22.(1)解:设P与Q碰撞前P的速度为 ,碰后P与Q的速度分别为 与 ,由动量守恒及机械能守恒定律有
由此解得
若
则
P、Q不可能发生第二次碰撞;
若
为使P从坡上滑下后再不能追上Q,应有
即
这导致
P、Q不可能发生第二次碰撞;为使二者能且只能发生一次碰撞,则k的值应满足的条件是
(2)解:为使P、Q能发生第二次碰撞,要求
对于第二次碰撞,令 和 分别表示碰后P和Q的速度,同样由动量守恒及机械能守恒定律有
由此解得 ,
若
则一定不会发生第三次碰撞,若
且
则会发生第三次碰撞,故为使第三次碰撞不会发生,要求P第三次从坡上滑下后速度的大小 不大于Q速度的大小 ,即
联立解得
由
可求得
解得
求交集即为所求
23.(1)解:根据动能定理
电极中央射入的离子在磁场中做匀速圆周运动,洛伦兹力提供向心力
得
根据几何关系,有得
联立得
(2)解:对人和宇宙飞船组成的系统,人往复运动对于系统而言合外力仍为0,由动量守恒知不会偏离。
(3)解:根据动量守恒
由动能定理
对时间内的飞船运用动量定理
联立,得
一、选择题(共15题)
1.如图,在光滑水平面上,轨道ABCD的质量M =0.4 kg,其中AB段是半径R=0.4 m的光滑弧,在B点与水平轨道BD相切,水平轨道的BC段粗糙,动摩擦因数μ=0.4,长L=3.5 m,C点右侧的轨道光滑,轨道的右端连接一轻质弹簧。 现有一质量m=0.1kg的小物体在A点正上方高为H=3.6m处由静止自由落下,恰沿A点切线滑入圆弧轨道,重力加速度g=10 m/s2。下列说法正确的是( )
A.小物体和轨道组成的系统在全过程中动量守恒
B.小物体第一次返回到A点时的速度为m/s
C.小物体第一次返回到A点时的速度为0
D.轨道M在水平面上运动的最大速率为2.0 m/s.
2.如图所示,大气球质量为100kg,载有质量为50kg的人(可以把人看做质点),静止在空气中距地面20m高的地方,气球下方悬一根质量可忽略不计的绳子,此人想从气球上沿绳慢慢下滑至地面,为了安全到达地面,则这绳长至少应为( )
A.20m B.30m C.40m D.50m
3.如图所示,甲木块的质量为 ,以速度 沿光滑水平地面向前运动,正前方有一静止的、质量为 的乙木块,乙上连有一轻质弹簧,甲木块与弹簧接触后( )
A.甲木块的动量守恒
B.乙木块的动量守恒
C.甲、乙两木块所组成的系统的动量守恒
D.甲、乙两木块所组成的系统的动能守恒
4.在光滑水平直路上停着一辆较长的木板车,车的左端站立一个大人,车的右端站立一个小孩.如果大人向右走,小孩(质量比大人小)向左走.他们的速度大小相同,则在他们走动过程中( )
A.车可能向右运动 B.车一定向左运动
C.车可能保持静止 D.无法确定
5.如图所示,A、B两物体的质量比mA:mB=4:3,它们原来静止在足够长的平板车C上,A、B间有一根被压缩了的弹簧,地面光滑。当弹簧突然释放后,且已知A、B组成的系统动量守恒。则有
A.A,B与C的动摩擦因数相等 B.A,B与C的动摩擦因数不相等
C.最终稳定时小车向右运动 D.A,B,C系统动量不守恒
6.关于物体的动量和冲量,下列说法不正确的是( )
A.物体所受合外力的冲量越大,它的动量也越大
B.物体所受合外力的冲量不为零,它的动量一定要改变
C.物体的动量增量的方向,就是它所受合外力的冲量的方向
D.物体所受合外力越大,它的动量变化就越快
7.如图所示,有一子弹穿过三块静止放置在光滑水平面上的相互接触质量分别为 m、2m、3m 的木块 A、B、C,设子弹穿过木块 A、B 、C 的时间分别为 t1、t2、t3,木块对子弹的阻力恒为 f,则子弹穿过三木块后,木块 A 的速度大小是( )
A. B.
C. D.
8.如图所示,站在车上的人,用锤子连续敲打小车。初始时,人、车、锤都静止。假设水平地面光滑,关于这一物理过程,下列说法正确的是( )
A.连续敲打可使小车持续向右运动
B.人、车和锤组成的系统机械能守恒
C.当锤子速度方向竖直向下时,人和车水平方向的总动量为零
D.人、车和锤组成的系统动量守恒
9.下列说法中正确的是( )
A.由 可知物体动量的变化率等于它受的合外力
B.冲量反映了力的作用对时间的累积效应,是一个标量
C.易碎品运输时要用柔软材料包装是为了减小冲量
D.玻璃杯掉在水泥地上易碎,是因为受到的冲量太大
10.如图,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触,现将摆球a向左拉开一小角度后释放。若两球的碰撞是弹性的,下列判断正确的是( )
A.第一次碰撞后的瞬间,两球的动能大小相等
B.第一次碰撞后的瞬间,两球的动量大小相等
C.第一次碰撞后的瞬间,两球的速度大小相等
D.第一次碰撞后,两球的最大摆角不相同
11.物体在恒定的合外力F作用下做直线运动,在时间Δt1内速度由0增大到v,在时间Δt2内速度由v增大到2v.设F在Δt1内做的功是W1,冲量是I1;在Δt2内做的功是W2,冲量是I2.那么( )
A.I2 = I1 W2 > W1 B.I2 < I1 W2 < W1
C.I2 > I1 W2 > W1 D.I2 = I1 W2 < W1
12.如图所示,质量均为M的b、d两个光滑斜面静止于水平面上,底边长度相等,b斜面倾角为30°,d斜面倾角为60°.质量均为m的小物块a和c分别从两个斜面顶端由静止自甶滑下,下滑过程中两斜面始终静止.小物块到达斜面底端的过程中,下列说法正确的是( )
A.两物块所受重力冲量相同
B.两物块所受重力做功的平均功率相同
C.两斜面对地面压力均小于
D.地面对两斜面的摩檫力均向左
13.如图甲,质量M=0.8 kg 的足够长的木板静止在光滑的水平面上,质量m=0.2 kg的滑块静止在木板的左端,在滑块上施加一水平向右、大小按图乙所示随时间变化的拉力F,4 s后撤去力F。若滑块与木板间的动摩擦因数μ=0.2,最大静摩擦力等于滑动摩擦力,重力加速度g=10 m/s2,则下列说法正确的是( )
A.0~4s时间内拉力的冲量为3.2 N·s
B.t= 4s时滑块的速度大小为9.5 m/s
C.木板受到滑动摩擦力的冲量为2.8 N·s
D.2~4s内因摩擦产生的热量为4J
14.下列说法正确的是( )
A.冲量的方向有可能和动量的方向相反
B.作用在物体上的合外力越大,物体动量的变化就越快
C.作用在物体上的合外力恒定不变时,物体的动量也保持恒定不变
D.动量变化量的大小一定和动量大小的变化量相同
15.如图所示,质量m1=0.3 kg的小车静止在光滑的水平面上,车长L=1.5 m,现有质量m2=0. 2 kg可视为质点的物块,以水平向右的速度v0从左端滑上小车,最后在车面上某处与小车保持相对静止。物块与车面间的动摩擦因数μ=0.5,取g=10 m/s2,则( )
A.物块滑上小车后,滑块和小车构成的系统动量守恒。
B.物块滑上小车后,滑块和小车构成的系统机械能守恒。
C.若v0=2m/s,则物块在车面上滑行的时间为0.24s;
D.若要保证物块不从小车右端滑出,则v0不得大于5m/s
二、填空题
16.一个物体静置于光滑水平面上,外面扣一质量为M的盒子,如图甲所示。现给盒子一初速度v0,此后,盒子运动的v-t图象呈周期性变化,如图乙所示,据此可知盒内物体的质量是 。
17.某同学用图所示的 “碰撞实验装置”研究直径相同的两个小球在轨道水平部分碰撞前后的动量关系。
①在实验中小球速度不易测量,可通过仅测量 解决这一问题。
A.小球做平抛运动的时间
B.小球做平抛运动的水平距离
C.小球做平抛运动的初始高度
D.小球释放时的高度
②图中PQ是斜槽,QR为水平槽,R为水平槽末端。利用铅垂线在记录纸上确定R的投影点O。实验时先使A球从斜槽上G处由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹;此后,再把B球放在R处,将A球再从G处由静止释放,与B球碰撞后在记录纸上分别留下A、B两球落点痕迹。由测量可知,碰撞前A球做平抛运动的水平距离为x0;碰撞后,A、B两球做平抛运动的水平距离分别为x1、x2。用天平称量A、B两球的质量分别为mA、mB。若两球相碰前后的动量守恒,其表达式可表示为 (用题目给出的物理量符号表示)。
18.如图甲所示,在探究碰撞中的不变量实验时,长木板光滑且处于水平,小车A的前端粘有橡皮泥,用手推动一下小车A,放手后小车A做匀速运动,然后与原来諍止在前方的小车B相碰并粘合在一起,之后继续匀速运动,在小车A后连着纸带,打点计时器电源周期为0.02s。
①若获得纸带如图乙所示,a为运动的起始点,从a点开始,每5个点取一个计数点,其中a、b、c、d、e都为计数点,并测得相邻计数点间距(已标在图上),则应选 段来计算A的碰前速度,应选 段来计算A和B碰后的共同速度(填ab、bc、cd或de)。
②已测得小车A(含橡皮泥)的质量mA=0.30kg,小车B(含撞针)的质量为mB=0.20kg,由以上测量结果可得碰前系统总动量为 kg·m/s,碰后系统总动量为 kg·m/s。(结果均保留三位有效数字)
19.光滑水平面上两小球a、b用不可伸长的松弛细绳相连。开始时a球静止,b球以一定速度运动直至绳被拉紧,然后两球一起运动,在此过程中两球的总动量 (填“守恒”或“不守恒”);机械能 (填“守恒”或“不守恒”)。
三、综合题
20.如图所示,质量M= 1kg的木板静止在足够长的固定光滑斜面上,斜面倾角 ,木板下端上表面恰与整直面内的光滑圆弧轨道BCD在D点相切,圆弧半径为R=11m,半径OB与竖直方向夹角为a=53°。一质量m=2kg(可视为质点)的小滑块以v0=6m/s的初速度从左侧水平桌面飞出,并恰好从B点沿切线进入圆弧轨道。已知滑块和木板之间的动摩擦因数μ=0.5,滑块不会从木板上端滑出,重力加速度g= 10m/s2,求∶
(1)滑块经过圆弧轨道上D点,圆弧轨道对它的弹力;
(2)木板上升过程中因摩擦产生的热量Q;
(3)木板下端第一次返回D点时,木板在斜面上运动的时间t。
21.如图所示,在倾角为30°的光滑斜面上放置一质量为m的物块B,B的下端连接一轻质弹簧,弹簧下端与挡板相连接,B平衡时,弹簧的压缩量为x0,O点为弹簧的原长位置。在斜面顶端另有一质量也为m的物块A,距物块B为3x0,现让A从静止开始沿斜面下滑,A与B相碰后立即一起沿斜面向下运动,但不粘连,它们到达最低点后又一起向上运动,并恰好回到O点(A、B均视为质点)。试求:
(1)A、B相碰后瞬间的共同速度的大小;
(2)A、B相碰前弹簧具有的弹性势能;
(3)若在斜面顶端再连接一光滑的半径R=x0的半圆轨道PQ,圆弧轨道与斜面相切于最高点P,现让物块A以初速度v从P点沿斜面下滑,与B碰后返回到P点还具有向上的速度,则v为多大时物块A恰能通过圆弧轨道的最高点?
22.如图所示,光滑的四分之一圆弧与光滑水平轨道在最低平滑连接。现有一质量为m的小球P沿光滑的四分之一圆弧上由静止开始下滑,与一质量为km(k>0,未知)的静止在光滑水平地面上的等大的小球Q发生正碰撞。设碰撞是弹性的,且一切摩擦不计。
(1)为使二者能且只能发生一次碰撞,则k的值应满足什么条件?
(2)为使二者能且只能发生两次碰撞,则k的值应满足什么条件?
23.如图甲所示的一种离子推进器,由离子源、间距为的平行金属板、和边长为的立方体构成,其中、正中间各有一个小孔且两小孔正对,工作原理简化图如图乙所示。氙离子从腔室中飘移过栅电极的速度大小可忽略不计,在栅电极、之间的匀强电场中加速,并从栅电极喷出,在加速氙离子(质量为、电荷量为)的过程中飞船获得推力,不计氙离子间的相互作用及重力影响。
(1)若该离子推进器固定在地面上实验时,在的右侧立方体间加垂直向里的匀强磁场,从电极中央射入的离子加速后经电板的中央点进入磁场,恰好打在立方体棱边的中点上。求、之间的电压与磁感应强度的关系式。
(2)若宇宙飞船处于悬浮状态(离子推进器停止工作),宇航员在飞船内从静止经多次往复运动后回到原位置不动,判断飞船最终是否偏离原位置?若偏离,请计算相对原位置的距离;若不偏离,请说明理由。
(3)若撤去离子推进器中的磁场,悬浮状态下的推进器在某段时间内喷射的个氙离子以速度通过栅极,该过程中离子和飞船获得的总动能占发动机提供能量的倍,飞船的总质量及获得的动力保持不变,已知发动机总功率为,求动力大小。
答案部分
1.D
【解答】A.小物体和轨道组成的系统全过程中只在水平方向上合外力为零,故全过程中水平方向动量守恒,A不符合题意;
BC.由题意分析可知,小物体第一次沿轨道返回到A点时小物体与轨道在水平方向的分速度相同,设为,假设此时小物体在竖直方向的分速度为,则对小物体和轨道组成的系统,由水平方向动量守恒得
由能量守恒得
解得
即小物体第一次返回到A点时的速度为
BC不符合题意;
D.由题意分析可知,当小物体沿运动到圆弧最低点B时轨道的速率最大,设为,假设此时小物体的速度大小为,则小物体和轨道组成的系统水平方向动量守恒,以初速度的方向为正方向,由动量守恒定律可得
由机械能守恒得
解得
D符合题意。
故答案为:D。
2.B
【解答】人与气球组成的系统动量守恒,设人的速度v1,气球的速度v2,设运动时间为t,以人与气球组成的系统为研究对象,以向下为正方向,由动量守恒得:m1v1-m2v2=0,则 ,解得:
则绳子长度:L=s球+s人=10m+20m=30m
即绳子至少长30m长。
故答案为:B
3.C
【解答】甲木块与弹簧接触后,由于弹簧弹力的作用,甲、乙的动量要发生变化,即甲、乙两物体的动量均不守恒;但对于甲、乙所组成的系统因所受合力的冲量为零,故动量守恒,AB不符合题意,C符合题意;甲、乙两木块所组成系统的动能,一部分转化为弹簧的势能,故系统动能不守恒,D不符合题意.
故答案为:C
4.B
【解答】系统动量守恒,且总动量为零,由于大人质量大于小孩,速度相同,因此大人与小孩的总动量向右,为满足动量守恒,车一定向左运动,ACD不符合题意,B符合题意.
故答案为:B.
5.B
【解答】AB.A、B组成的系统动量守恒,则AB两物体所受的摩擦力应该大小相等方向相反,系统所受合外力才为0,因为AB质量不相等所以动摩擦因数不相等,A不符合题意,B符合题意。
CD.ABC三物体所组成的系统动所受合外力为0,动量守恒。最终稳定时,三个物体应该都处于静止状态,CD不符合题意。
故答案为:B。
6.A
【解答】A.物体所受合外力的冲量越大,它的动量变化量越大,并不是动量越大,A错误,符合题意;
B.物体所受合外力的冲量不为零,它的动量一定要改变,B正确,不符合题意;
C.物体的动量增量的方向,就是它所受合外力的冲量的方向,C正确,不符合题意;
D.根据动量定理和牛顿第二定律可知,物体所受合外力等于动量的变化率,所以合外力越大,动量变化就越快,D正确,不符合题意。
故答案为:A。
7.C
【解答】A与B分离时三者的速度是相等的,分离后,A的速度不变,在分离前子弹对系统的作用力使A、B与C的速度增大,由动量定理得
所以
故答案为:C。
8.C
【解答】A.人、车和锤看做一个系统处在光滑水平地面上,水平方向所受合外力为零,故水平方向动量守恒,总动量始终为零,当大锤有相对大地向左的速度时,车有向右的速度,当大锤有相对大地向右的速度时,车有向左的速度,故车来回运动,A不符合题意;B.大锤击打小车时,发生的不是完全弹性碰撞,系统机械能有损耗,B不符合题意;C.大锤的速度竖直向下时,没有水平方向的速度,因为水平方向总动量恒为零,故人和车的总动量也为零,C符合题意;D.人、车和锤水平方向动量守恒,因为大锤会有竖直方向的加速度,故竖直方向合外力不为零,竖直动量不守恒,系统总动量不守恒,D不符合题意。
故答案为:C
9.A
【解答】A.由 可知物体动量的变化率等于它受的合外力,所以A符合题意;
B.冲量反映了力的作用对时间的累积效应,是一个矢量,所以B不符合题意;
C.易碎品运输时要用柔软材料包装是为了延长作用时间,减小冲击力,所以C不符合题意;
D.玻璃杯掉在水泥地上易碎,是因为作用时间短,受到的冲击力太大,所以D不符合题意;
故答案为:A。
10.C
【解答】两球在碰撞前后,水平方向不受外力,故水平方向两球组成的系统动量守恒,由动量守恒定律有:mv0=mv1+3mv2,两球碰撞是弹性的,故机械能守恒,即: mv02= mv12+ 3mv22,解两式得:v1=- ,v2= ,可见第一次碰撞后的瞬间,两球的速度大小相等;因两球质量不相等,故两球碰后的动量大小不相等,方向相反,动能也不相等,AB不符合题意,C符合题意;两球碰后上摆过程,机械能守恒,故上升的最大高度相等,另摆长相等,故两球碰后的最大摆角相同,D不符合题意。 故答案为:C
11.A
【解答】根据动能定理得:
则W1<W2。
根据动量定理得,I1=mv-0=mv
I2=2mv-mv=mv
知I1=I2.
故答案为:A。
12.A,C
【解答】设斜面的倾角为 时下滑的时间为 ,设斜面底端长度为 ,则斜面长为 ,根据牛顿第二定律可得加速度为: ,根据运动学公式可得: ,解得: ,由于两个斜面的倾角分别为 和 ,则可知 、 沿斜面下滑的时间相等;
A、两物块所受重力冲量 相同, A符合题意;
B、重力做功的平均功率为 ,由于 不同,所以两物块所受重力做功的平均功率不相同, B不符合题意;
C、小物块加速下滑过程中在竖直方向的加速度方向向下,处于失重状态,以整体为研究对象,两斜面对地面压力均小于 ,C符合题意;
D、以整体为研究对象,小物块水平方向的加速度方向都向右,而斜面的加速度为零,根据 可知地面对两斜面的摩擦力均向右,D不符合题意.
故答案为:AC
13.B,C,D
【解答】A.冲量的定义式: ,所以F-t图像面积代表冲量,所以0-4 s时间内拉力的冲量为
A不符合题意;
B.木块相对木板滑动时:对木板:
对木块:
联立解得: ,
所以0时刻,即相对滑动,对滑块:
解得4s时滑块速度大小: B符合题意;
C.4s时,木板的速度
撤去外力后,木板加速,滑块减速,直到共速,根据动量守恒:
解得: ,
对木板根据动量定理可得:
C符合题意;
D.0-2s内,对m:
解得:
对M
解得v2=1m/s
2-4s内:对m
;
对M
所以
D符合题意。
故答案为:BCD
14.A,B
【解答】冲量的方向与动量变化的方向相同,有可能和动量的方向相反,A符合题意;根据动量定理可知,合外力等于动量的变化率,则作用在物体上的合外力越大,物体动量的变化就越快,B符合题意;作用在物体上的合外力恒定不变时,合外力的冲量不为零,则物体的动量要发生变化,C不符合题意;当物体做曲线运动时,动量变化量的大小和动量大小的变化量不相同,D不符合题意.
故答案为:AB
15.A,C,D
【解答】由于地面光滑,所以物块和小车构成的系统动量守恒,A符合题意;由于物块和小车之间有摩擦力,所以系统机械能不守恒,B不符合题意;设物块与小车的共同速度为v,以水平向右的方向为正方向,根据动量守恒定律有 ,设物块与车面间的滑动摩擦力为 ,则 对物块应用动量定理有 ,解得 ,代入数据得 ,C符合题意;要使物块恰好不从车面上滑出,须物块到车面最右端时与小车有共同的速度,设其为v′,则 ,由功能关系有 ,代入数据解得 ,D符合题意;
故答案为:ACD
16.M
【解答】设物体的质量为m,t0时刻受盒子碰撞获得速度v,根据动量守恒定律得:Mv0=mv①
3t0时刻物体与盒子右壁碰撞使盒子速度又变为v0,说明物体速度变为零,且碰撞是弹性碰撞,由机械能守恒有: M = mv2②
联立①②解得m=M
17.B; ;
【解答】(1)因为平抛运动的速度等于射程与落地时间的比值,而当高度一定时,落地时间一定,所以可以测量射程代替速度,故答案为:B;(2) 要验证动量守恒定律定律,即验证: ,小球离开轨道后做平抛运动,它们抛出点的高度相等,在空中的运动时间t相等,上式两边同时乘以t得, ,若两球相碰前后的动量守恒,得:
18.bc;de;1.04;1.03
【解答】①推动小车由静止开始运动,故小车有个加速过程,在碰撞前做匀速直线运动,即在相同的时间内通过的位移相同,Bc段为匀速运动的阶段,故答案为:bc计算碰前的速度;碰撞过程是一个变速运动的过程,而A和B碰后的共同运动时做匀速直线运动,故在相同的时间内通过相同的位移,故应选de段来计算碰后共同的速度;②A碰前的速度
碰后共同速度
碰前系统总动量
碰后系统总动量
19.守恒;不守恒
【解答】将a b组成系统,对系统受力分析知合外力为零,故系统动量守恒;而在此过程拉力对b做负功,机械能不守恒。
20.(1)由几何关系知滑块经过B点时
滑块在B到D的过程由动能定理得
解得
滑块在D点由牛顿第二定律
解得
方向垂直与斜面向上;
(2)滑块冲上木板后,设经过 时间达到共同速度 ,则在这个过程中
取沿斜面向上为正方向,对滑块有
对木板有
解得
此过程中,滑块的位移
木板的位移
此后过程中滑块与木板保持相对静止,所以上升过程中摩擦生热为
(3)设木板下端返回D点时速度为 ,共速后对整体有
解得
取沿斜面向下为正方向有
解得
所以木板在斜面上运动的时间为
21.(1)解:A与B碰撞前后,设A的速度分别是 和
A下滑过程中,机械能守恒,有:
解得: ①
又因A与B碰撞过程中,动量守恒,有:
②
联立①②得
(2)解:碰后,A、B和弹簧组成的系统在运动过程中,机械能守恒。
则有:
又由(1)得
代入解得: ③
(3)解:设物块A在最高点C的速度是
物块A恰能通过圆弧轨道的最高点C点时,重力提供向心力,得:
C点相对于O点的高度,如图所示:
物块从O到C的过程中机械能守恒,得:
设A与B碰撞后共同的速度为 ,碰撞前A的速度为 ,
物块A从P到与B碰撞前的过程中机械能守恒,得:
A与B碰撞的过程中动量守恒,得:
A与B碰撞结束后到O的过程中机械能守恒,得: ⑩
由于A与B不粘连,到达O点时,滑块B开始受到弹簧的拉力,A与B分离。
综合上述式子解得:
22.(1)解:设P与Q碰撞前P的速度为 ,碰后P与Q的速度分别为 与 ,由动量守恒及机械能守恒定律有
由此解得
若
则
P、Q不可能发生第二次碰撞;
若
为使P从坡上滑下后再不能追上Q,应有
即
这导致
P、Q不可能发生第二次碰撞;为使二者能且只能发生一次碰撞,则k的值应满足的条件是
(2)解:为使P、Q能发生第二次碰撞,要求
对于第二次碰撞,令 和 分别表示碰后P和Q的速度,同样由动量守恒及机械能守恒定律有
由此解得 ,
若
则一定不会发生第三次碰撞,若
且
则会发生第三次碰撞,故为使第三次碰撞不会发生,要求P第三次从坡上滑下后速度的大小 不大于Q速度的大小 ,即
联立解得
由
可求得
解得
求交集即为所求
23.(1)解:根据动能定理
电极中央射入的离子在磁场中做匀速圆周运动,洛伦兹力提供向心力
得
根据几何关系,有得
联立得
(2)解:对人和宇宙飞船组成的系统,人往复运动对于系统而言合外力仍为0,由动量守恒知不会偏离。
(3)解:根据动量守恒
由动能定理
对时间内的飞船运用动量定理
联立,得
同课章节目录
- 第1章 碰撞与动量守恒
- 1.1 动量变化与冲量的关系
- 1.2 动量守恒定律
- 1.3 动量守恒定律的案例分析
- 1.4 美妙的守恒定律
- 第2章 机械振动
- 2.1 简谐运动
- 2.2 物体做简谐运动的原因
- 2.3 摆钟的物理原理
- 2.4 单摆振动的周期
- 2.5 受迫振动与共振
- 第3章 机械波
- 3.1 机械波的产生
- 3.2 机械波的描述
- 3.3 机械波案例分析
- 3.4 惠更斯原理 波的反射与折射
- 3.5 波的干涉与衍射
- 3.6 多普勒效应
- 第4章 光及其应用
- 4.1 光的折射
- 4.2 全反射与光导纤维
- 4.3 光的干涉
- 4.4 用双缝干涉仪测量光的波长
- 4.5 光的衍射
- 4.6 光的偏振与立体电影
- 4.7 激光
