4.1.3 三角形的中线、角平分线基础训练(含答案)
文档属性
| 名称 | 4.1.3 三角形的中线、角平分线基础训练(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《4.1.3 三角形的中线、角平分线》
知识点一 三角形的中线
1.如图,若AD是的中线,则下列结论错误的是( )
A.AD平分
B.
C.AD平分BC
D.
2.如图,,则中EC边上的中线是( )
A.AD
B.AE
C.AF
D.无法确定
3.三角形的三条中线相交于一点,这个点一定在三角形的___________,这个点叫做三角形的___________.
4.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
5.如图,BD=DE=EC,则线段AE是 的中线.
6.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是 .
7.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
知识点二 三角形的重心
8.三角形的角平分线是( )
A.射线
B.线段
C.直线
D.以上都有可能
9.如图,如果,则AM为___________的角平分线,AN为__________的角平分线.
10.如图,已知P是△ABC的重心,连接AP并延长交BC于点D,若△ABC的面积为20,则△ADC的面积为( )
A.10
B.8
C.6
D.5
11.有一质地均匀的三角形铁皮,若阿龙想用一根木棒撑住此铁皮,则支撑点应设在该三角形的 处最恰当.
知识点三 三角形的角平分线
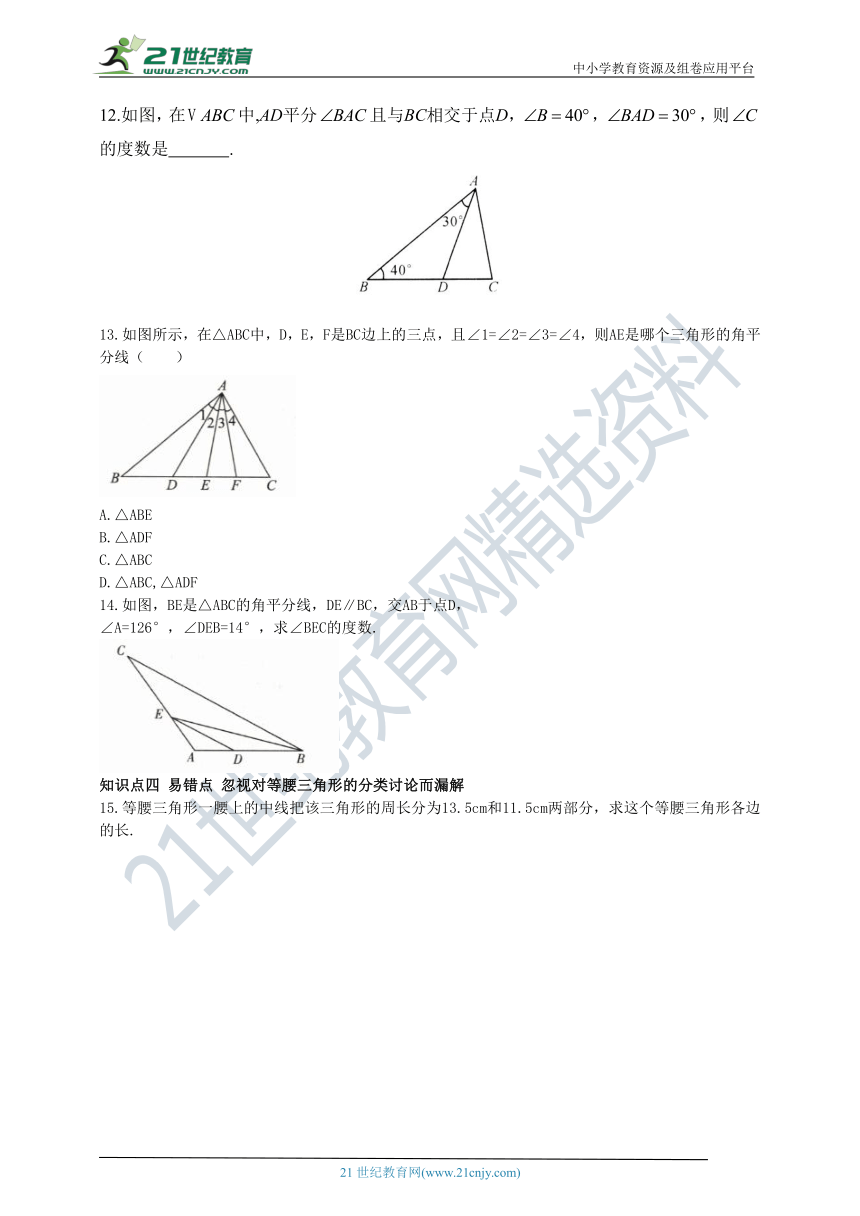
12.如图,在中,AD平分且与BC相交于点D,,,则的度数是 .
13.如图所示,在△ABC中,D,E,F是BC边上的三点,且∠1=∠2=∠3=∠4,则AE是哪个三角形的角平分线( )
A.△ABE
B.△ADF
C.△ABC
D.△ABC,△ADF
14.如图,BE是△ABC的角平分线,DE∥BC,交AB于点D,
∠A=126°,∠DEB=14°,求∠BEC的度数.
知识点四 易错点 忽视对等腰三角形的分类讨论而漏解
15.等腰三角形一腰上的中线把该三角形的周长分为13.5cm和11.5cm两部分,求这个等腰三角形各边的长.
参考答案
1.A 2.C 3.内部 重心
4.答案:B
解析:根据三角形的面积公式以及三角形的中线定义知,三角形一边上的中线把三角形分成了等底同高的两个三角形,所以它们的面积相等.
5.答案:△ADC
解析:BD=DE=EC,则E是CD的中点,则AE是△ADC的中线.
6.答案:9
解析:因为BD是△ABC的中线,所以AD=CD.因为△ABD的周长为11,AB=5,BC=3,所以△BCD的周长是11-(5-3)=9.故答案为9.
7.答案:因为AD是BC边上的中线,所以BD=CD.因为△ADC的周长比△ABD的周长多5cm,所以(AC+AD+CD)-(AB+AD+BD)=5cm.所以AC-AB=5cm.即AB=(AC-5)cm.因为AB+AC=13cm,所以AC=9cm.
解析:
8.B 9.ABN
10.答案:A
解析:因为P是△ABC的重心,所以AD是△ABC的中线,所以△ADC的面积等于△ABC面积的一半.又因为△ABC的面积为20,所以△ADC的面积为10.故选A.
11.答案:重心
解析:阿龙想用一根木棒撑住此铁皮,则支撑点应设在该三角形的重心处,故答案为重心.
12.80°
13.答案:D
解析:因为∠2=∠3,所以AE是△ADF的角平分线;因为∠1=∠2=∠3=∠4,所以∠1+∠2=∠3+∠4,即∠BAE=∠CAE,所以AE是△ABC的角平分线.
14.答案:因为BE是△ABC的角平分线,所以∠CBE=∠ABE.因为DE∥BC,∠DEB=14°,所以∠DEB=∠CBE=14°,所以∠ABE=14°.因为∠A=126°,∠A+∠ABE+∠AEB=80°,∠BEC+∠AEB=180°,所以∠BEC=∠A+∠ABE=126°+14°=140°.
解析:
15.答案:设在△ABC中,AB=AC,BD是AC边上的中线,依题意,当AB>BC时,AB-BC=13.5-11.5=2,即AB=BC+2,所以2(BC+2)+BC=13.5+11.5,解得BC=7,AB=AC=BC+2=9.
当AB综上,这个等腰三角形三边的长分别为9cm,9cm,7cm或cm, cm,cm.
解析:易错警示 这道题是以文字叙述的形式给出的,没有图形,也没有字母.因此,可以先根据文字叙述画出图形,标注字母,利用图形减小题目难度.由于腰和底边不相等造成的中线把三角形的周长分成不相等的两部分,因此既要考虑到腰比底边长,又要考虑到底边比腰长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
《4.1.3 三角形的中线、角平分线》
知识点一 三角形的中线
1.如图,若AD是的中线,则下列结论错误的是( )
A.AD平分
B.
C.AD平分BC
D.
2.如图,,则中EC边上的中线是( )
A.AD
B.AE
C.AF
D.无法确定
3.三角形的三条中线相交于一点,这个点一定在三角形的___________,这个点叫做三角形的___________.
4.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
5.如图,BD=DE=EC,则线段AE是 的中线.
6.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是 .
7.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
知识点二 三角形的重心
8.三角形的角平分线是( )
A.射线
B.线段
C.直线
D.以上都有可能
9.如图,如果,则AM为___________的角平分线,AN为__________的角平分线.
10.如图,已知P是△ABC的重心,连接AP并延长交BC于点D,若△ABC的面积为20,则△ADC的面积为( )
A.10
B.8
C.6
D.5
11.有一质地均匀的三角形铁皮,若阿龙想用一根木棒撑住此铁皮,则支撑点应设在该三角形的 处最恰当.
知识点三 三角形的角平分线
12.如图,在中,AD平分且与BC相交于点D,,,则的度数是 .
13.如图所示,在△ABC中,D,E,F是BC边上的三点,且∠1=∠2=∠3=∠4,则AE是哪个三角形的角平分线( )
A.△ABE
B.△ADF
C.△ABC
D.△ABC,△ADF
14.如图,BE是△ABC的角平分线,DE∥BC,交AB于点D,
∠A=126°,∠DEB=14°,求∠BEC的度数.
知识点四 易错点 忽视对等腰三角形的分类讨论而漏解
15.等腰三角形一腰上的中线把该三角形的周长分为13.5cm和11.5cm两部分,求这个等腰三角形各边的长.
参考答案
1.A 2.C 3.内部 重心
4.答案:B
解析:根据三角形的面积公式以及三角形的中线定义知,三角形一边上的中线把三角形分成了等底同高的两个三角形,所以它们的面积相等.
5.答案:△ADC
解析:BD=DE=EC,则E是CD的中点,则AE是△ADC的中线.
6.答案:9
解析:因为BD是△ABC的中线,所以AD=CD.因为△ABD的周长为11,AB=5,BC=3,所以△BCD的周长是11-(5-3)=9.故答案为9.
7.答案:因为AD是BC边上的中线,所以BD=CD.因为△ADC的周长比△ABD的周长多5cm,所以(AC+AD+CD)-(AB+AD+BD)=5cm.所以AC-AB=5cm.即AB=(AC-5)cm.因为AB+AC=13cm,所以AC=9cm.
解析:
8.B 9.ABN
10.答案:A
解析:因为P是△ABC的重心,所以AD是△ABC的中线,所以△ADC的面积等于△ABC面积的一半.又因为△ABC的面积为20,所以△ADC的面积为10.故选A.
11.答案:重心
解析:阿龙想用一根木棒撑住此铁皮,则支撑点应设在该三角形的重心处,故答案为重心.
12.80°
13.答案:D
解析:因为∠2=∠3,所以AE是△ADF的角平分线;因为∠1=∠2=∠3=∠4,所以∠1+∠2=∠3+∠4,即∠BAE=∠CAE,所以AE是△ABC的角平分线.
14.答案:因为BE是△ABC的角平分线,所以∠CBE=∠ABE.因为DE∥BC,∠DEB=14°,所以∠DEB=∠CBE=14°,所以∠ABE=14°.因为∠A=126°,∠A+∠ABE+∠AEB=80°,∠BEC+∠AEB=180°,所以∠BEC=∠A+∠ABE=126°+14°=140°.
解析:
15.答案:设在△ABC中,AB=AC,BD是AC边上的中线,依题意,当AB>BC时,AB-BC=13.5-11.5=2,即AB=BC+2,所以2(BC+2)+BC=13.5+11.5,解得BC=7,AB=AC=BC+2=9.
当AB
解析:易错警示 这道题是以文字叙述的形式给出的,没有图形,也没有字母.因此,可以先根据文字叙述画出图形,标注字母,利用图形减小题目难度.由于腰和底边不相等造成的中线把三角形的周长分成不相等的两部分,因此既要考虑到腰比底边长,又要考虑到底边比腰长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
