2021-2022学年人教版数学七年级下册5.2.2 平行线的判定 课件(21张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册5.2.2 平行线的判定 课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 769.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
5.2.2 平行线的判定
同位角相等,两直线平行
内错角相等,两直线平行
人教版数学七级下册
同位角相等,两直线平行
观察下面每幅图中的直线a,b,它们分别平行吗?你能验证吗?
导入
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.
做一做
知识讲解
难点突破
同学们利用手中提前准备好的教具,分小组讨论并回答以下问题:
1、在转动木条a的过程中, ∠1, ∠2 的大小关系分为哪几种情况?
2、木条a、 b位置关系有哪些?
知识讲解
同学们,在转动木条a的过程中, ∠1, ∠2 的大小关系分为哪几种情况?
通过观察,在转动木条a的过程中, ∠1, ∠2 的大小关系分为∠1<∠2, ∠1= ∠2 ,∠1> ∠2 三种情况
那么同学们,木条a、 b位置关系有哪些?
分组汇报中
第三小组很认真
木条a、 b位置关系两种:相交和平行
第五小组积极主动:
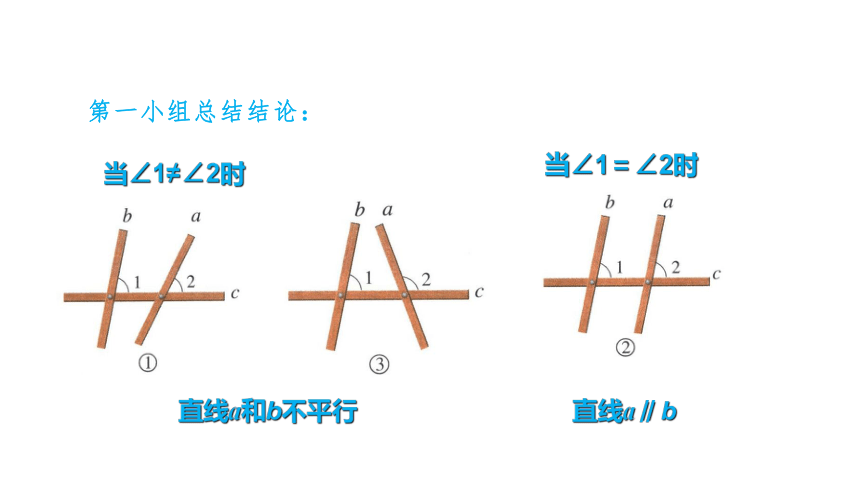
第一小组总结结论:
当∠1=∠2时
当∠1≠∠2时
直线a和b不平行
直线a∥b
判断两条直线平行的方法:
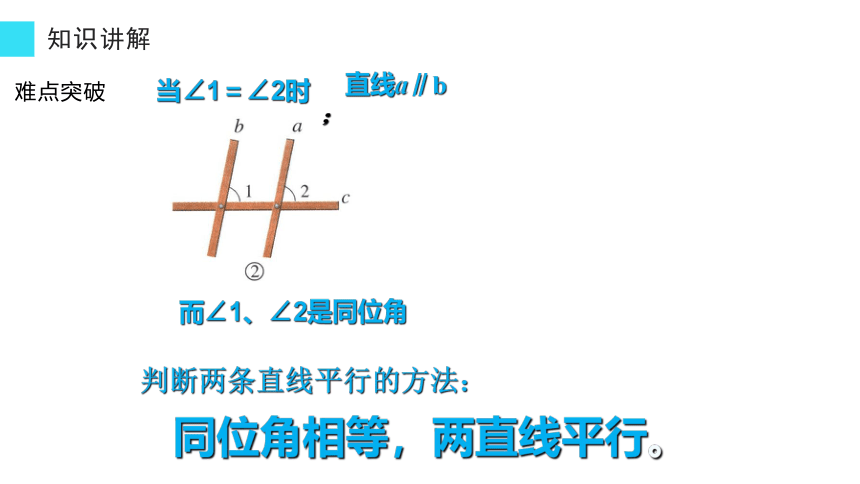
当∠1=∠2时
直线a∥b
;
同位角相等,两直线平行。
而∠1、∠2是同位角
知识讲解
难点突破
例1:如图,在屋架上要加一根横梁DE,已知∠B=32°,要使DE∥BC,则∠ADE必须等于多少度?为什么?
A
D
E
F
C
B
知识讲解
难点突破
答: ∠ADE =32°,理由如下。
因为同位角相等,两直线平行。 而∠ADE 和∠B是同位角, ∠B=32°,所以要使DE∥BC,则∠ADE必须等于32°,
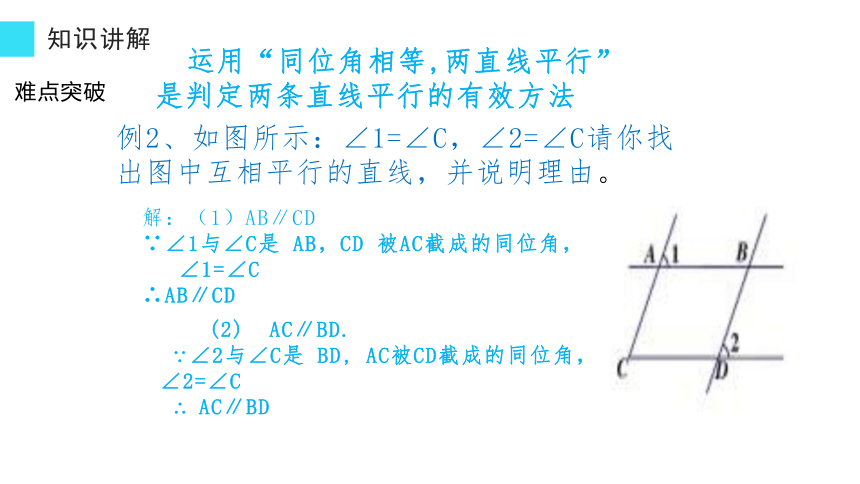
例2、如图所示:∠1=∠C,∠2=∠C请你找出图中互相平行的直线,并说明理由。
(2) AC∥BD.
∵∠2与∠C是 BD, AC被CD截成的同位角,
∠2=∠C
∴ AC∥BD
解:(1)AB∥CD
∵∠1与∠C是 AB,CD 被AC截成的同位角,
∠1=∠C
∴AB∥CD
运用“同位角相等,两直线平行”
是判定两条直线平行的有效方法
知识讲解
难点突破
1、如图,一张纸上画有a、b两条线段,请你设计一个方案,判断这两条线段是否平行?
课堂练习
难点巩固
a
b
c
有同学说了,可以添加一条截线c,测量同位角是不是相等,如果相等,就有两条线段平行。
2、如图,在同一平面内,如果两条直线b、c都垂直于同一条直线a,那么这两条直线平行吗 为什么
解: ∵ a⊥b,c⊥a(已知)
∴ ∠1=90°,∠2=90°(垂直定义).
∴ ∠1=∠2=90°(等量代换)
∵ ∠1=∠2, ∠1和∠2是同位角
∴ b∥c (同位角相等,两直线平行).
课堂练习
难点巩固
【课堂小结】
小结
1、判断两条直线平行的方法:同位角相等,两直线平行
2、同位角相等,两直线平行在生产生活和数学分析中都 有广泛的应用。
内错角相等,两直线平行
导入
14
回顾 & 思考
1、同位角相等,两直线平行。
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
同位角相等,两直线平行。
即∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
下图中,如果∠1=∠7,
能得出AB∥CD吗
思考
解:∵∠1=∠7(已知)
∠1=∠3(对顶角相等)
∴ ∠7=∠3(等量代换)
∴ AB∥CD(同位角相等,
两直线平行)
D
F
C
7
3
E
1
B
A
5
知识讲解
难点突破
2.内错角相等,两直线平行。
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
内错角相等,两直线平行。
即∵∠1=∠3(已知)
∴a∥b(内错角相等,两直线平行)
课堂练习
17
难点巩固
1.如下图.
(1)如果∠B =∠1,那么根据____________________,可得AD∥BC;
(2)如果∠D =∠1,那么根据____________________,可得AB∥CD。
同位角相等,两直线平行
内错角相等,两直线平行
(第1题)
(第1题)
2.如图:在四边形ABCD中,∠1=40°,∠2=40°,AD与BC平行吗?为什么?
解:∵ ∠1=40°,∠2=40°(已知)
∴∠1=∠2
∴AD∥BC(内错角相等,两直线平行)
1.如图,
(1)从∠1=∠2,可以推 ∥ ,
考考你
d
b
a
内错角相等,两直线平行
同位角相等,两直线平行.
3
3
a
b
1
2
5
4
c
(2)从∠2=∠ , 可以推出 c∥d ,
理由是
理由是
【课堂小结】
小结
通过这节课的学习,
你有哪些收获
议一议
判定方法:内错角相等, 两直线平行.
感 谢 聆 听
5.2.2 平行线的判定
同位角相等,两直线平行
内错角相等,两直线平行
人教版数学七级下册
同位角相等,两直线平行
观察下面每幅图中的直线a,b,它们分别平行吗?你能验证吗?
导入
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.
做一做
知识讲解
难点突破
同学们利用手中提前准备好的教具,分小组讨论并回答以下问题:
1、在转动木条a的过程中, ∠1, ∠2 的大小关系分为哪几种情况?
2、木条a、 b位置关系有哪些?
知识讲解
同学们,在转动木条a的过程中, ∠1, ∠2 的大小关系分为哪几种情况?
通过观察,在转动木条a的过程中, ∠1, ∠2 的大小关系分为∠1<∠2, ∠1= ∠2 ,∠1> ∠2 三种情况
那么同学们,木条a、 b位置关系有哪些?
分组汇报中
第三小组很认真
木条a、 b位置关系两种:相交和平行
第五小组积极主动:
第一小组总结结论:
当∠1=∠2时
当∠1≠∠2时
直线a和b不平行
直线a∥b
判断两条直线平行的方法:
当∠1=∠2时
直线a∥b
;
同位角相等,两直线平行。
而∠1、∠2是同位角
知识讲解
难点突破
例1:如图,在屋架上要加一根横梁DE,已知∠B=32°,要使DE∥BC,则∠ADE必须等于多少度?为什么?
A
D
E
F
C
B
知识讲解
难点突破
答: ∠ADE =32°,理由如下。
因为同位角相等,两直线平行。 而∠ADE 和∠B是同位角, ∠B=32°,所以要使DE∥BC,则∠ADE必须等于32°,
例2、如图所示:∠1=∠C,∠2=∠C请你找出图中互相平行的直线,并说明理由。
(2) AC∥BD.
∵∠2与∠C是 BD, AC被CD截成的同位角,
∠2=∠C
∴ AC∥BD
解:(1)AB∥CD
∵∠1与∠C是 AB,CD 被AC截成的同位角,
∠1=∠C
∴AB∥CD
运用“同位角相等,两直线平行”
是判定两条直线平行的有效方法
知识讲解
难点突破
1、如图,一张纸上画有a、b两条线段,请你设计一个方案,判断这两条线段是否平行?
课堂练习
难点巩固
a
b
c
有同学说了,可以添加一条截线c,测量同位角是不是相等,如果相等,就有两条线段平行。
2、如图,在同一平面内,如果两条直线b、c都垂直于同一条直线a,那么这两条直线平行吗 为什么
解: ∵ a⊥b,c⊥a(已知)
∴ ∠1=90°,∠2=90°(垂直定义).
∴ ∠1=∠2=90°(等量代换)
∵ ∠1=∠2, ∠1和∠2是同位角
∴ b∥c (同位角相等,两直线平行).
课堂练习
难点巩固
【课堂小结】
小结
1、判断两条直线平行的方法:同位角相等,两直线平行
2、同位角相等,两直线平行在生产生活和数学分析中都 有广泛的应用。
内错角相等,两直线平行
导入
14
回顾 & 思考
1、同位角相等,两直线平行。
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
同位角相等,两直线平行。
即∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
下图中,如果∠1=∠7,
能得出AB∥CD吗
思考
解:∵∠1=∠7(已知)
∠1=∠3(对顶角相等)
∴ ∠7=∠3(等量代换)
∴ AB∥CD(同位角相等,
两直线平行)
D
F
C
7
3
E
1
B
A
5
知识讲解
难点突破
2.内错角相等,两直线平行。
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
内错角相等,两直线平行。
即∵∠1=∠3(已知)
∴a∥b(内错角相等,两直线平行)
课堂练习
17
难点巩固
1.如下图.
(1)如果∠B =∠1,那么根据____________________,可得AD∥BC;
(2)如果∠D =∠1,那么根据____________________,可得AB∥CD。
同位角相等,两直线平行
内错角相等,两直线平行
(第1题)
(第1题)
2.如图:在四边形ABCD中,∠1=40°,∠2=40°,AD与BC平行吗?为什么?
解:∵ ∠1=40°,∠2=40°(已知)
∴∠1=∠2
∴AD∥BC(内错角相等,两直线平行)
1.如图,
(1)从∠1=∠2,可以推 ∥ ,
考考你
d
b
a
内错角相等,两直线平行
同位角相等,两直线平行.
3
3
a
b
1
2
5
4
c
(2)从∠2=∠ , 可以推出 c∥d ,
理由是
理由是
【课堂小结】
小结
通过这节课的学习,
你有哪些收获
议一议
判定方法:内错角相等, 两直线平行.
感 谢 聆 听
