18.2.1矩形的判定 课件(共17张PPT)
文档属性
| 名称 | 18.2.1矩形的判定 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 20:46:29 | ||
图片预览




文档简介
(共17张PPT)
18.2.1 矩形
( 第2课时)
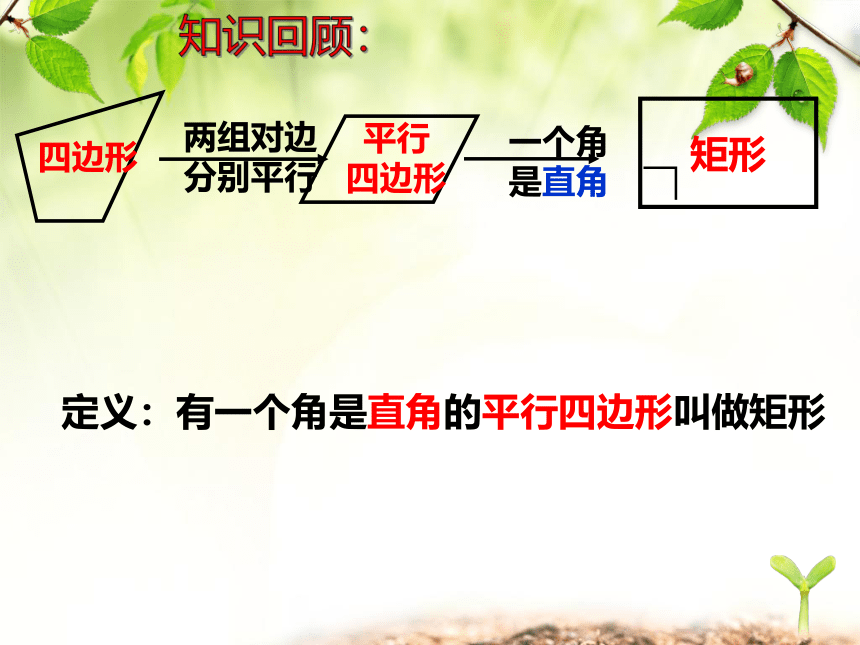
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
定义:有一个角是直角的平行四边形叫做矩形
∵在□ABCD中,∠A=90°
∴四边形ABCD是矩形
定义:有一个角是直角的平行四边形叫做矩形.
数学语言:
判定1
A
B
C
D
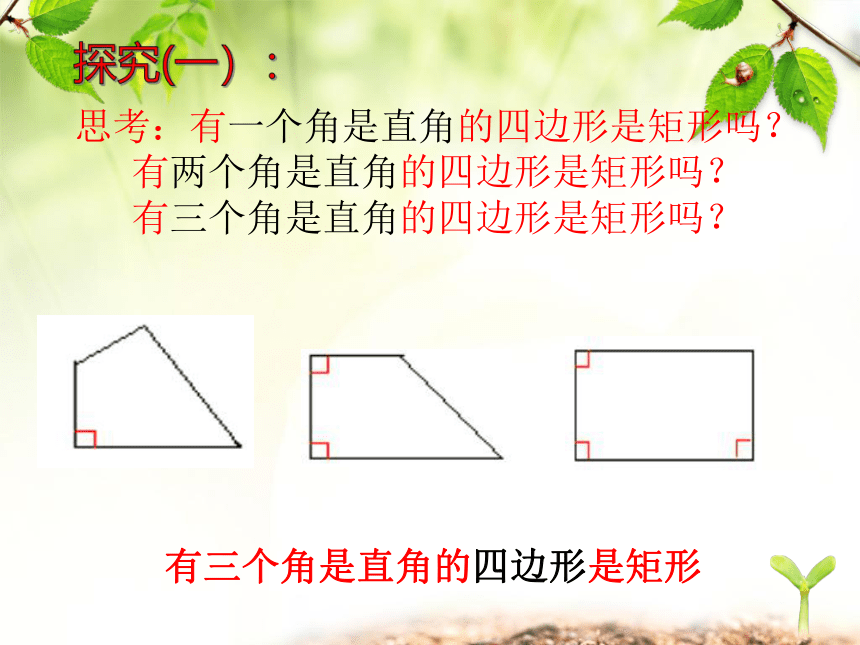
有三个角是直角的四边形是矩形
思考:有一个角是直角的四边形是矩形吗?
有两个角是直角的四边形是矩形吗?
有三个角是直角的四边形是矩形吗?
命题1 有三个角是直角的四边形是矩形
A
B
C
D
已知:在四边形ABCD中,
∠A= ∠B= ∠C=90°
求证:四边形ABCD是矩形
证明:∵ ∠A= ∠B= ∠C=90°
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
∴四边形ABCD是矩形
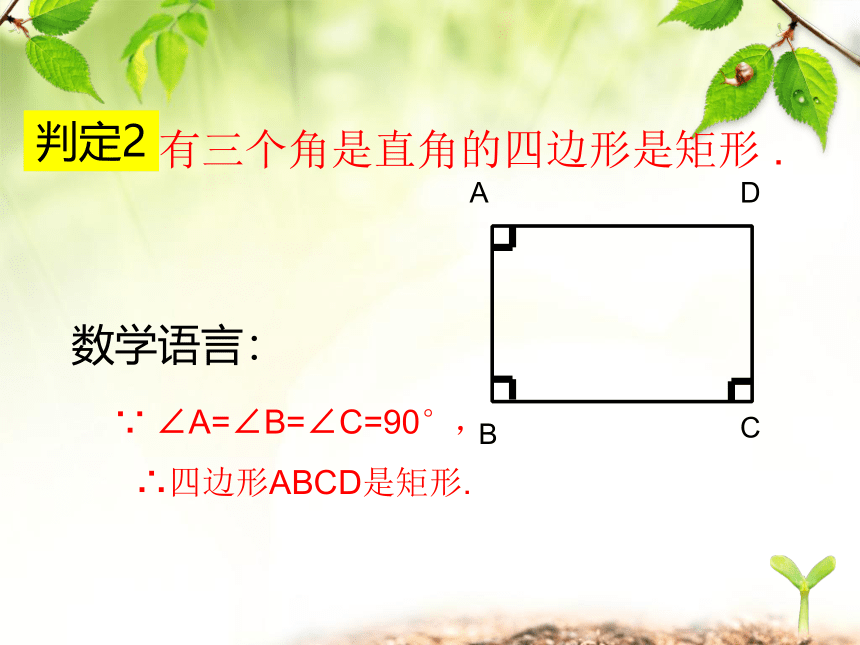
有三个角是直角的四边形是矩形 .
A
B
C
D
∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
数学语言:
判定2
情境:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:
对角线相等的平行四边形是矩形 。
已知:四边形ABCD是矩形,求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌ △DCB
∴AC = BD
2:矩形的对角线相等.
命题
∵四边形 ABCD是矩形, ∴AB=DC
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
∴ ∠ABC=∠DCB
命题2:对角线相等的平行四边形是矩形。
已知:在□ ABCD,AC=BD
求证:□ ABCD是矩形
A
B
C
D
证明:
又∵BC=CB, 且AC=DB
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
(有一个角是直角的平行四边形是矩形)
A
B
C
D
O
∵四边形ABCD是平行四边形且AC=BD
∴四边形ABCD是矩形
对角线相等的平行四边形是矩形
几何语言:
判定3
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
(对角线相等且互相平分的四边形是矩形)
有三个角是直角的四边形是矩形
方法1:(定义法)
方法3:
方法2:
例2:如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°,求∠OAB的度数.
A
B
C
D
O
证明:
∵ 四边形ABCD是平行四边形
∴ AC=2OA,BD=2OD
∴ ∠DAB=90°
又∵ OA=OD
∴ AC=BD
∴ 四边形ABCD是矩形
又∵ ∠OAD=50°
∴ ∠OAB=90-50°= 40°
∵ 四边形ABCD是矩形
练习:如图,M为 ABCD边AD的中点MB=MC,
求证:四边形ABCD是矩形。
A
B
C
D
M
证明:∵ 四边形ABCD是平行四边形
∴ AB∥CD,AB=CD
∴ ∠A+ ∠D=180°
∵M是AD的中点
∴AM=DM
∵MB=MC
∴ △ABM≌△DCM(SSS)
∴∠A=∠D=90°
∴ 四边形ABCD是矩形
1、能够判断一个四边形是矩形的条件是( )
A、 对角线相等 B、 对角线垂直
C、对角线互相平分且相等 D、对角线垂直且相等
2、矩形的一组邻边长分别是3cm和4cm,则它的对角线
长是 cm。
3、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是( )
A 菱形 B 平行四边形
C 矩形 D 不能确定
C
5
C
反馈检测
4、已知:如图, ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
(对角线相等且互相平分的四边形是矩形)
有三个角是直角的四边形是矩形
方法1:(定义法)
方法3:
方法2:
18.2.1 矩形
( 第2课时)
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
定义:有一个角是直角的平行四边形叫做矩形
∵在□ABCD中,∠A=90°
∴四边形ABCD是矩形
定义:有一个角是直角的平行四边形叫做矩形.
数学语言:
判定1
A
B
C
D
有三个角是直角的四边形是矩形
思考:有一个角是直角的四边形是矩形吗?
有两个角是直角的四边形是矩形吗?
有三个角是直角的四边形是矩形吗?
命题1 有三个角是直角的四边形是矩形
A
B
C
D
已知:在四边形ABCD中,
∠A= ∠B= ∠C=90°
求证:四边形ABCD是矩形
证明:∵ ∠A= ∠B= ∠C=90°
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
∴四边形ABCD是矩形
有三个角是直角的四边形是矩形 .
A
B
C
D
∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
数学语言:
判定2
情境:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:
对角线相等的平行四边形是矩形 。
已知:四边形ABCD是矩形,求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌ △DCB
∴AC = BD
2:矩形的对角线相等.
命题
∵四边形 ABCD是矩形, ∴AB=DC
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
∴ ∠ABC=∠DCB
命题2:对角线相等的平行四边形是矩形。
已知:在□ ABCD,AC=BD
求证:□ ABCD是矩形
A
B
C
D
证明:
又∵BC=CB, 且AC=DB
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
(有一个角是直角的平行四边形是矩形)
A
B
C
D
O
∵四边形ABCD是平行四边形且AC=BD
∴四边形ABCD是矩形
对角线相等的平行四边形是矩形
几何语言:
判定3
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
(对角线相等且互相平分的四边形是矩形)
有三个角是直角的四边形是矩形
方法1:(定义法)
方法3:
方法2:
例2:如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°,求∠OAB的度数.
A
B
C
D
O
证明:
∵ 四边形ABCD是平行四边形
∴ AC=2OA,BD=2OD
∴ ∠DAB=90°
又∵ OA=OD
∴ AC=BD
∴ 四边形ABCD是矩形
又∵ ∠OAD=50°
∴ ∠OAB=90-50°= 40°
∵ 四边形ABCD是矩形
练习:如图,M为 ABCD边AD的中点MB=MC,
求证:四边形ABCD是矩形。
A
B
C
D
M
证明:∵ 四边形ABCD是平行四边形
∴ AB∥CD,AB=CD
∴ ∠A+ ∠D=180°
∵M是AD的中点
∴AM=DM
∵MB=MC
∴ △ABM≌△DCM(SSS)
∴∠A=∠D=90°
∴ 四边形ABCD是矩形
1、能够判断一个四边形是矩形的条件是( )
A、 对角线相等 B、 对角线垂直
C、对角线互相平分且相等 D、对角线垂直且相等
2、矩形的一组邻边长分别是3cm和4cm,则它的对角线
长是 cm。
3、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是( )
A 菱形 B 平行四边形
C 矩形 D 不能确定
C
5
C
反馈检测
4、已知:如图, ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
(对角线相等且互相平分的四边形是矩形)
有三个角是直角的四边形是矩形
方法1:(定义法)
方法3:
方法2:
