柱、锥的体积
图片预览



文档简介
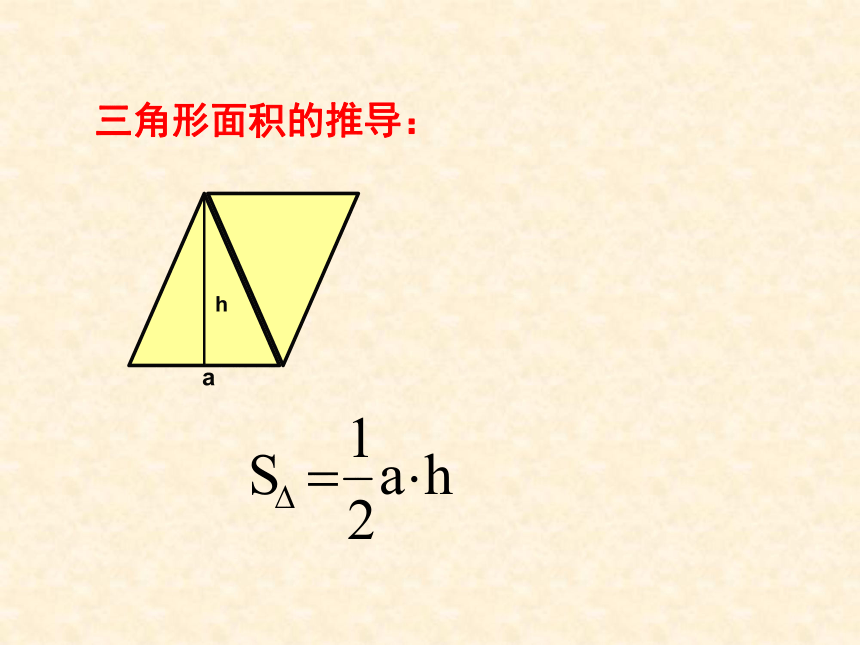
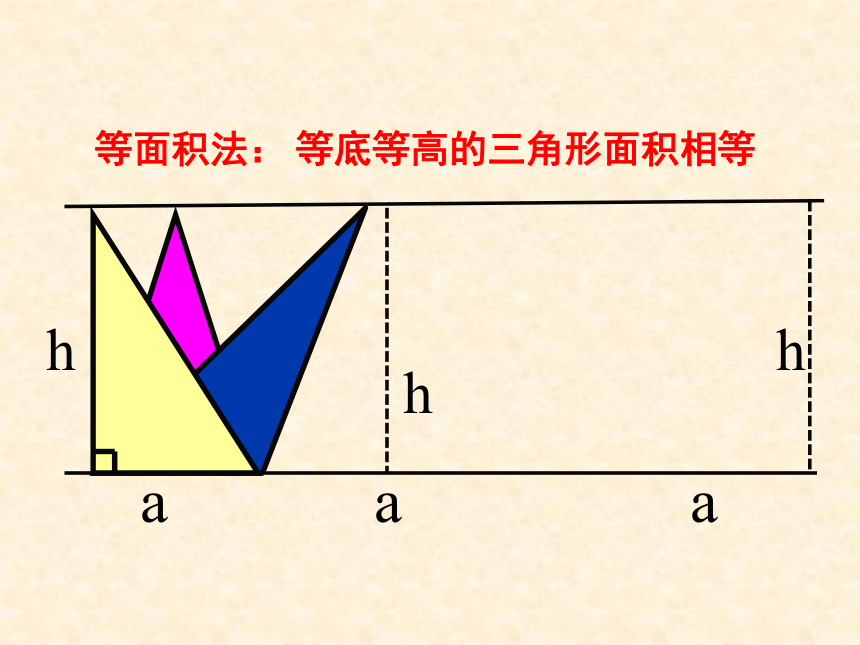
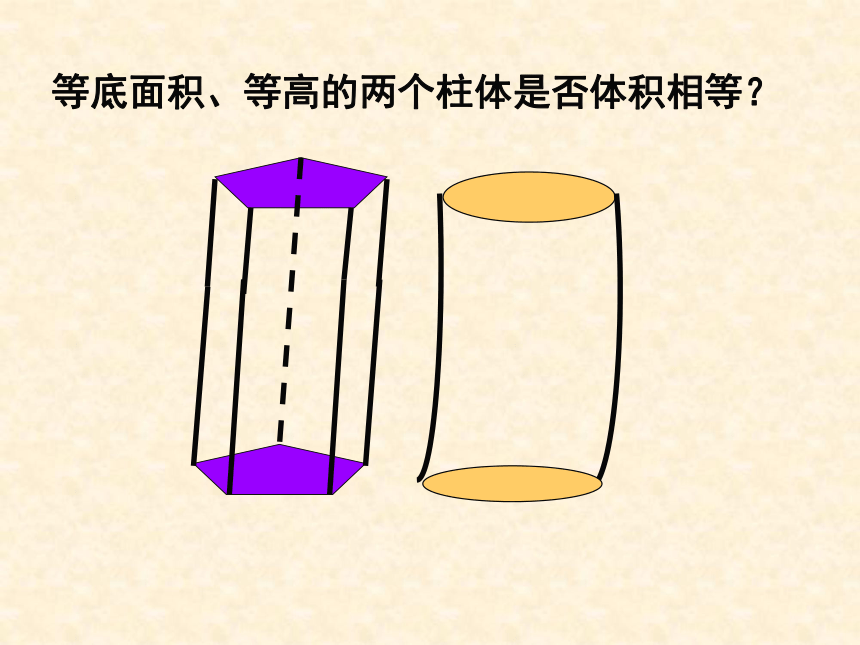
课件20张PPT。1.1.7 柱、锥的体积ah三角形面积的推导:等底等高的三角形面积相等等面积法:等底面积、等高的两个柱体是否体积相等?一. 祖暅原理 祖暅原理:幂势既同,则积不容异. 也就是说,夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等. 祖暅原理是推导柱、锥、台和球体积公式的基础和纽带,原理中含有三个条件:
条件一是两个几何体夹在两个平行平面之间;
条件二是用平行于两个平行平面的任何一平面可截得两个平面;
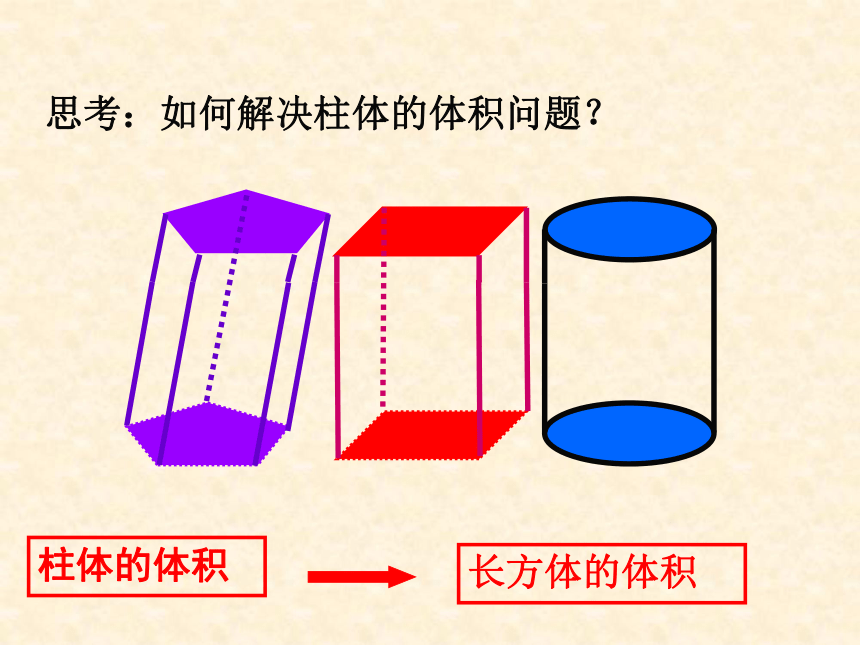
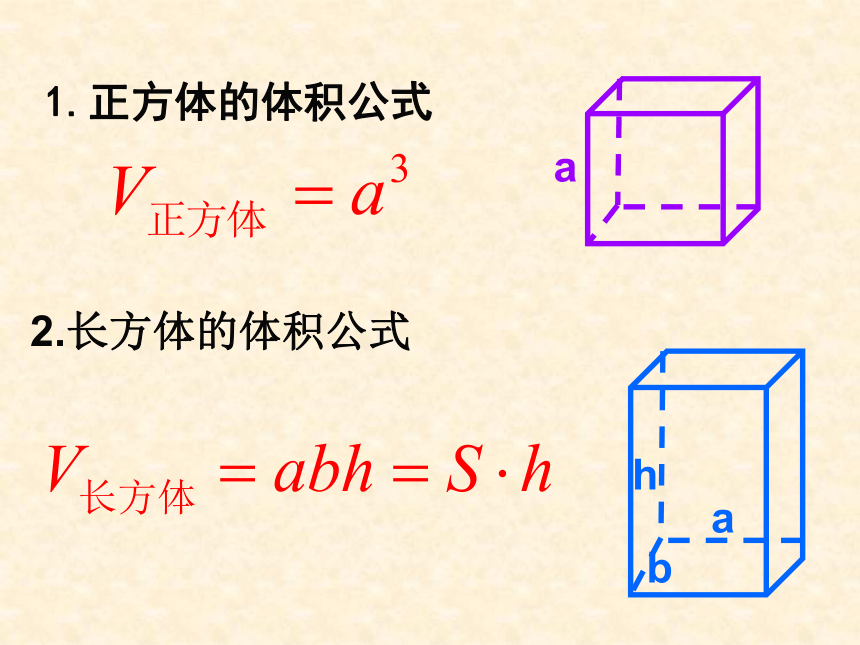
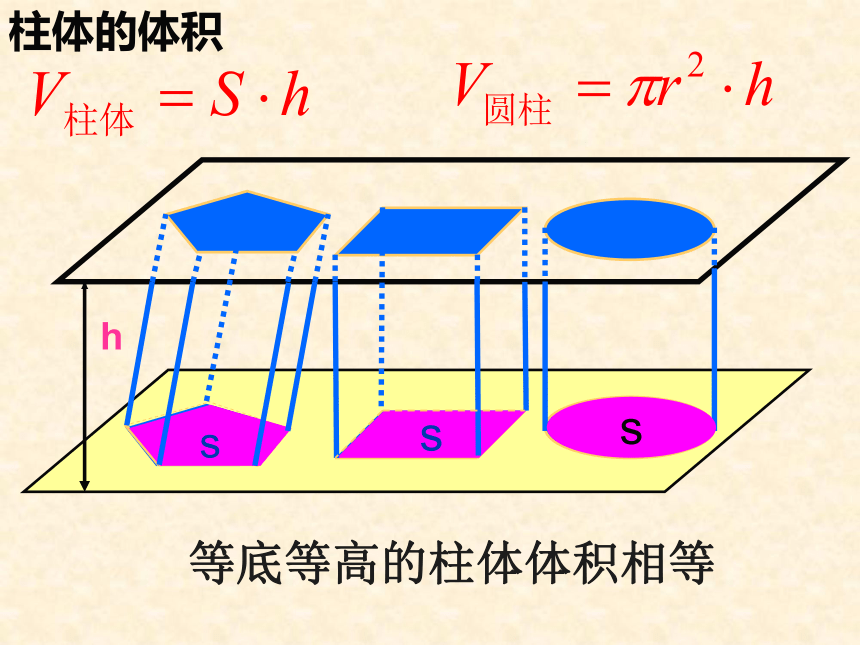
条件三是两个截面的面积总相等,这三个条件缺一不可,否则结论不成立.思考:如何解决柱体的体积问题?柱体的体积长方体的体积1.正方体的体积公式2.长方体的体积公式ahab柱体的体积sSS等底等高的柱体体积相等sS’S’ssh锥体的体积V柱=shV锥=?祖暅原理例1、在长方体ABCD-A/B/C/D/中,用截面截下一个棱锥C-A/DD/,求棱锥C-A/DD/的体积与剩余部分的体积之比。ADCBC/D/B/A/Sh练习1、已知直三棱柱底面的一边长为2cm,另两边长都为3cm,侧棱长为4cm,求它的体积。例2、(1)如果圆柱的底面半径不变,要使它的体积扩大到原来的5倍,那么需要把它的高扩大到原来的多少倍?
(2) 如果圆柱的高不变,半径扩大到原来的多少倍才能使它的体积扩大到原来的5倍。思考题如图,三棱柱 ,棱 到面 的距离是a,求
祖暅原理:幂势既同,则积不容异。水平截面面积高体积+说明:
等底面积、等高的两个柱体或锥体的体积相等。祖暅原理柱、锥的体积
条件一是两个几何体夹在两个平行平面之间;
条件二是用平行于两个平行平面的任何一平面可截得两个平面;
条件三是两个截面的面积总相等,这三个条件缺一不可,否则结论不成立.思考:如何解决柱体的体积问题?柱体的体积长方体的体积1.正方体的体积公式2.长方体的体积公式ahab柱体的体积sSS等底等高的柱体体积相等sS’S’ssh锥体的体积V柱=shV锥=?祖暅原理例1、在长方体ABCD-A/B/C/D/中,用截面截下一个棱锥C-A/DD/,求棱锥C-A/DD/的体积与剩余部分的体积之比。ADCBC/D/B/A/Sh练习1、已知直三棱柱底面的一边长为2cm,另两边长都为3cm,侧棱长为4cm,求它的体积。例2、(1)如果圆柱的底面半径不变,要使它的体积扩大到原来的5倍,那么需要把它的高扩大到原来的多少倍?
(2) 如果圆柱的高不变,半径扩大到原来的多少倍才能使它的体积扩大到原来的5倍。思考题如图,三棱柱 ,棱 到面 的距离是a,求
祖暅原理:幂势既同,则积不容异。水平截面面积高体积+说明:
等底面积、等高的两个柱体或锥体的体积相等。祖暅原理柱、锥的体积
