2021-2022学年湘教版八年级数学下册2.7正方形同步优生辅导测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学下册2.7正方形同步优生辅导测评(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 360.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 16:15:10 | ||
图片预览




文档简介
2021-2022学年湘教版八年级数学下册《2-7正方形》同步优生辅导测评(附答案)
一.选择题(共8小题,满分40分)
1.如图,在正方形ABCD中,AB=4,点E在对角线AC上,若S△ABE=5,则△CDE的面积为( )
A.3 B.4 C.5 D.6
2.如图,在边长为4的正方形ABCD中,点E、点F分别是BC、AB上的点,连接DE、DF、EF,满足∠DEF=∠DEC.若AF=1,则EF的长为( )
A.2.4 B.3.4 C. D.
3.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(0,2),点B的坐标为(﹣3,0),则点C到y轴的距离是( )
A.6 B.5 C.4 D.3
4.如图,在正方形ABCD中,点E在对角线AC上,EF⊥AB于点F,EG⊥BC于点G,连接DE,若AB=10,AE=3,则ED的长度为( )
A.7 B.2 C. D.
5.如图,在正方形ABCD中,动点E在BC边上(点E与点B不重合),∠DAE的平分线AF与CD边交于点M,与BC边的延长线交于点F,连接EM.对于下列四个结论:①AE=EF;②若CM=CE,则AF=2BC;③若EM⊥AF,则CM=DM;④存在点E,使点E与点D关于直线AF对称.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
6.如图所示,O为正方形ABCD的中点,BE平分∠DBC,交DC于点E,延长BC到F,使FC=EC,连结DF交B的延长线于点H,连结OH交DC于点G,连结HC,则下列结论:①OH∥BF;②∠CHF=45°;③GH=BC;④三角形BDF是直角三角形.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
7.如图,点E在正方形ABCD的对角线AC上,且EC=AE,Rt△FEG的两直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD边长为4,则重叠部分四边形EMCN的面积为( )
A.2 B.4 C.6 D.8
8.如图,正方形ABCO和正方形DEFO的顶点A,O,E在同一直线l上,且EF=,AB=3,给出下列结论:①∠COD=45°;②AE=6;③CF=BD=;④△COF的面积是.其中正确的结论为( )
A.①③ B.①④ C.②③ D.①③④
二.填空题(共8小题,满分40分)
9.如图,点E,F在正方形ABCD的对角线AC上,AC=10,AE=CF=3,则四边形BFDE的面积为 .
10.如图,两个正方形边长分别为2、a(a>2),图中阴影部分的面积为 .
11.如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的度数是 度.
12.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为 .
13.如图,在正方形ABCD中,,E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN.则MN的长为 .
14.如图,已知正方形ABCD的边长为6,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=2,则FM的长为 .
15.如图,AD是△ABC的高,∠BAC=45°,若BD=10,DC=3,则高AD的长度为 .
16.如图,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,DE=10,则AD的长为 .
三.解答题(共5小题,满分40分)
17.如图,矩形ABCD对角线AC,BD相交于O,OE⊥BC,垂足为E.
(1)求证:OE=CD;
(2)若点F是OD的中点,连接EF交OC于点G,连接AF.
①求证:GE=GF.
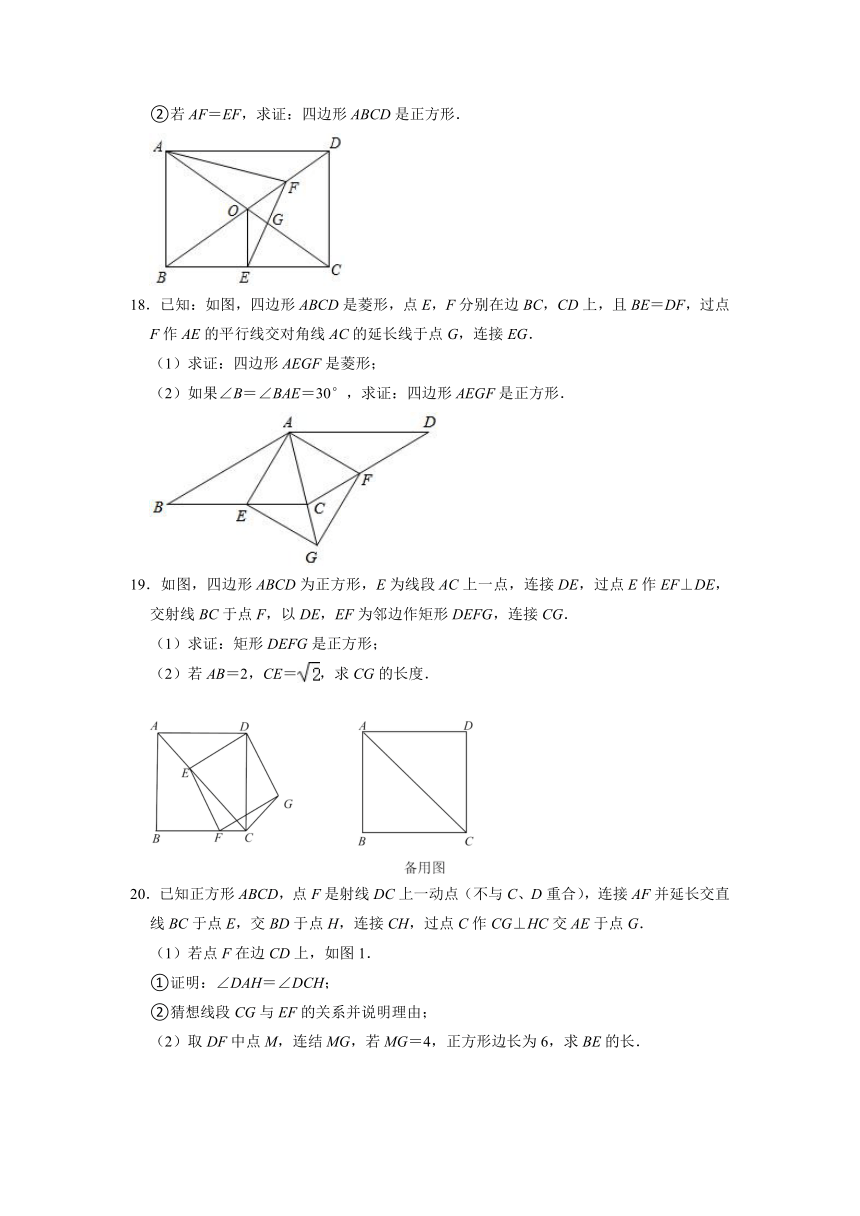
②若AF=EF,求证:四边形ABCD是正方形.
18.已知:如图,四边形ABCD是菱形,点E,F分别在边BC,CD上,且BE=DF,过点F作AE的平行线交对角线AC的延长线于点G,连接EG.
(1)求证:四边形AEGF是菱形;
(2)如果∠B=∠BAE=30°,求证:四边形AEGF是正方形.
19.如图,四边形ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度.
20.已知正方形ABCD,点F是射线DC上一动点(不与C、D重合),连接AF并延长交直线BC于点E,交BD于点H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想线段CG与EF的关系并说明理由;
(2)取DF中点M,连结MG,若MG=4,正方形边长为6,求BE的长.
21.如图所示,在正方形ABCD中,AB=10,点O为对角线交点,BE=CF,连接EF,过点O作OG⊥EF交BC边于G,点G始终在BC边上,并且不与点B、点C重合,连接OE、OF、EG.
(1)求证:OE=OF;
(2)请求出∠EOG的度数?
(3)试求出△BEG的周长;
(4)若AE=AO,请直接写出四边形BEOG的面积.
参考答案
一.选择题(共8小题,满分40分)
1.解:过点E作MN∥AD,交AB于点M,CD于点N,
∵四边形ABCD是正方形,
∴AD⊥AB,AD⊥CD,AB=BC=CD=DA=4,
∵MN∥AD,
∴MN⊥AB,MN⊥CD,
∵S△ABE=AB EM=×4×EM=2EM=5,
∴EM=,
∴EN=AD﹣EM=AB﹣EM=4﹣=,
∴S△CDE=CD EN=×4×=3,
故选:A.
2.解:如图,在EF上截取EG=EC,连接DG,
∵四边形ABCD是正方形,
∴∠A=∠C=90°,AB=BC=4,
在△DCE和△DGE中,
,
∴△DCE≌△DGE(SAS),
∴∠DGE=∠C=90°,DG=DC,
∵∠A=∠C=90°,AB=BC=4,
∴∠DGF=∠A=90°,DG=DA,
在Rt△DAF和Rt△DGF中,
,
∴Rt△DAF≌Rt△DGF(HL),
∴AF=GF=1,
∵EG=EC,
∴BE=BC﹣EC=4﹣EG,EF=EG+FG=EG+1,BF=AB﹣AF=4﹣1=3,
在Rt△BEF中,根据勾股定理,得
BE2+BF2=EF2,
∴(4﹣EG)2+32=(EG+1)2,
解得EG=2.4,
∴EF=EG+FG=2.4+1=3.4.
∴EF的长为3.4.
故选:B.
3.解:过点C作CE⊥x轴于点E,如图,
则点C到y轴的距离为OE.
∵点A的坐标为(0,2),点B的坐标为(﹣3,0),
∴OA=2,OB=3.
∵CE⊥x轴,
∴∠CEB=90°.
∴∠ECB+∠EBC=90°.
∵四边形ABCD是正方形,
∴BC=AB,∠CBA=90°.
∴∠EBC+∠ABO=90°.
∴∠ECB=∠ABO.
在△CBE和△BAO中,
,
∴△CBE≌△BAO(AAS).
∴EB=OA=2.
∴OE=OB+BE=3+2=5.
∴点C到y轴的距离是5.
故选:B.
4.解:如图,连接BE,
∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,AB=AD,
∵AE=AE,
∴△ABE≌△ADE(SAS),
∴BE=DE,
∵EF⊥AB于点F,AE=3,
∴AF=EF=3,
∵AB=10,
∴BF=7,
∴BE==,
∴ED=.
故选:C.
5.解:∵AF平分∠DAE,
∴∠DAF=∠EAF,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAF=∠EFA,
∴∠EFA=∠EAF,
∴AE=EF,故①正确;
若CM=CE,
则DM=BE,
∵∠B=∠D=90°,AB=AD,
在△ABE和△ADM中,
,
∴△ABE≌△ADM(SAS),
∴∠BAE=∠DAM=∠EAF=30°,
∴∠F=30°,
∴AF=2AB,
∴AF=2BC,故②正确;
若EM⊥AF,
∴M是AF的中点,
∴AM=FM,
在△ADM和△FMC中,
,
∴△ADM≌△FMC(AAS),
∴CM=DM,故③正确;
只有当点E和点D重合时,
才有点E与点D关于直线AF对称.
与题意不符,故④错误.
综上所述:其中正确结论有①②③,共3个,
故选:C.
6.解:∵四边形ABCD是正方形,
∴∠BDC=∠DBC=45°,∠BCE=∠DCF=90°,BC=DC,
∵EC=FC,
∴△BCE≌△DCF(SAS),
∴∠EBC=∠FDC,∠BEC=∠F,
∵BE平分∠DBC,
∴∠DBH=∠FBH=∠FDC=22.5°,
∴∠BDF=∠BDC+∠FDC=45°+22.5°=67.5°,∠F=∠BEC=90°﹣∠EBC=90°﹣22.5°=67.5°,故④错误,不符合题意;
∴∠BDF=∠F,
∴BD=BF,△BDF是等腰三角形,
∴DH=HF,即点H是DF的中点,
∴CH=HF,
∴∠HCF=∠F=67.5°,
∴∠CHF=180°﹣∠HCF﹣∠F=45°,故②正确,符合题意;
∵O为BD的中点,
∴OH是三角形BDF的中位线,
∴OH∥BF,故①正确,符合题意;
∴GH=CF,
在正方形ABCD中,BD=BC,
∴BC=BD,
∵BF=BD,CF=BF﹣BC,
∴CF=BD﹣BD=BD,
∴GH=BD=×BC=BC,故③错误,不符合题意;
∴正确的有①②两个,
故选:B.
7.解:连接ED,
∵AE=EC,
∴点E是AC的中点,
∵四边形ABCD是正方形,
∴∠DEC=90°,DE=EC,∠EDN=∠ECM=45°,
∴∠DEN+∠NEC=90°,
∵EF⊥EG,
∴∠MEC+∠NEC=90°,
∴∠DEN=∠CEM,
∴△MEC≌△NED(ASA),
∴S△MEC=S△NED,
∴S四边形EMCN=S△MEC+S△NEC=S△NED+S△NEC=S△DEC,
∵正方形ABCD的边长为4,
∴AC=4,
∴ED=EC=2,
∴S△DEC==×2×2=4,
∴重叠部分四边形EMCN的面积为4.
故选:B.
8.解:①∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,
故正确;
②∵EF=,
∴OE=2,
∵AO=AB=3,
∴AE=AO+OE=2+3=5,
故错误;
③作DH⊥AB于H,作FG⊥CO交CO的延长线于G,
则FG=1,
CF===,
BH=3﹣1=2,
DH=3+1=4,
BD===2,
故错误;
④△COF的面积S△COF=×3×1=,
故正确;
∴其中正确的结论为①④,
故选:B.
二.填空题(共8小题,满分40分)
9.解:连接BD交AC于点O,
∵四边形ABCD为正方形,
∴OA=OB=OC=OD,AC⊥BD,
又∵AE=CF,
∴OE=OF,
∴四边形BEDF为平行四边形,
∵EF垂直平分BD,
∴EB=ED,
∴四边形BEDF是菱形,
∴BD=AC=10,
∵AE=CF=3,
∴EF=4,
∴四边形BFDE的面积为BD EF=×10×4=20.
故答案为:20.
10.解:阴影部分的面积=
11.解:∵四边形ABCD是正方形,
∴AB=BC=AD=CD,∠ABC=90°,∠ADG=∠CDG,∠ABD=45°,
∵GD=GD,
∴△ADG≌△CDG,
∴∠AGD=∠CGD,
∵∠CGD=∠EGB,
∴∠AGD=∠EGB,
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,
∴BE=BC,∠EBC=150°,
∴∠BEC=∠ECB=15°,
∴∠BGE=180°﹣∠BEC﹣∠EBG=180°﹣15°﹣60°﹣45°=60°,
∴∠AGD=60°
故答案为60.
12.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∴AB2=4,
∴AB=2,
故答案为:2.
13.解:连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴AB=CD=BC=2,AB∥CD,∠C=90°,
∴∠AEM=∠GDM,∠EAM=∠DGM,
∵M为DE的中点,
∴ME=MD,
在△AEM和GDM中,
,
∴△AEM≌△GDM(AAS),
∴AM=MG,AE=DG=AB=CD,
∴CG=CD=,
∵点N为AF的中点,
∴MN=FG,
∵F为BC的中点,
∴CF=BC=,
∴FG==2,
∴MN=1,
故答案为:1.
14.解:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
,
∴△DEF≌△DMF(SAS),
∴EF=MF,
设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
∴FM=5.
故答案为:5.
15.解:以AD为边作正方形ADEF,在EF上截取FQ=BD=10.
在△ABD和△AQF中,
,
∴△ABD≌△AQF(SAS),
∴AB=AQ,∠BAD=∠FAQ,
∵∠BAC=45°,
∴∠BAD+∠DAC=45°,
∴∠DAC+∠FAQ=45°,
即∠CAQ=45°,
∴∠BAC=∠CAQ.
在△BAC和△QAC中,
,
∴△BAC≌△QAC(SAS),
∴BC=CQ=BD+CD=13.
设AD=x,则QE=x﹣10,CE=x﹣3.
在Rt△CQE中,∠E=90°,
∵CE2+QE2=CQ2,
∴(x﹣3)2+(x﹣10)2=132,
解得:x1=15,x2=﹣2(不合舍去),
∴AD=15.
故答案为:15.
16.解:过C作CG⊥AD于G,并延长DG,使GF=BE,
在直角梯形ABCD中∵AD∥BC,∠A=∠B=90°,∠CGA=90°,AB=BC,
∴四边形ABCG为正方形,
∴AG=BC=12,
∵∠DCE=45°,
∵CE=CF,∠DCF=∠DCE,DC=DC,
∴△ECD≌△FCD(SAS).
∴ED=DF=10,
∴DE=DF+DG=BE+GD,
设AD=x,则DG=12﹣x,
∴AE=14﹣x,
在Rt△AED中,∵DE2=AD2+AE2,
∴102=(14﹣x)2+x2
∴x=8,x=6
即AD=8或6.
故答案为:8或6.
三.解答题(共5小题,满分40分)
17.(1)证明:∵矩形ABCD对角线AC,BD相交于O,
∴O是BD的中点,
∵OE⊥BC,DC⊥BC,
∴OE∥DC,
∴E是BC的中点,
∴OE是△BCD的中位线,
∴OE=CD;
(2)①证明:如图,取OB的中点H,连接EH,
∵点E是BC边的中点,
∴EH∥OC,
∴=,
∵四边形ABCD为矩形,
∴OB=OD,
∵点F是线段OD的中点,
∴OF=OH,
∴GE=GF;
②证明:如图,过点F作FM⊥BC于M,连接FC,
∵OB=OC,
∵点E是BC边的中点,
∴OE⊥BC,
∴OE∥FM∥CD,
∵点F是线段OD的中点,
∴点M是线段EC的中点,
∴FE=FC,
∵AF=FE,
∴AF=CF,
∵OA=OC,
∴OF所在直线是AC的垂直平分线,
∴DA=DC,
∴矩形ABCD为正方形.
18.(1)证明:∵菱形ABCD,
∴AB=AD,∠B=∠D,∠BAC=∠DAC,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,∠BAE=∠DAF,
∴∠EAG=∠FAG,
∵FG∥AE,
∴∠EAG=∠FGA,
∴∠FAG=∠FGA,
∴FG=AF=AE,
∵FG∥AE,
∴四边形AEGF是平行四边形,
又∵AF=AE,
∴四边形AEGF是菱形;
(2)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠B+∠BAD=180°,
∵∠B=∠BAE=30°,
∵△ABE≌△ADF,
∴∠BAE=∠DAF=30°,
∴∠BAD=180°﹣∠B=150°,
∴∠EAF=∠BAD﹣∠BAE﹣∠DAF=150°﹣30°﹣30°=90°,
∵四边形AEGF是菱形,
∴四边形AEGF是正方形.
19.(1)证明:如图1,作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED,
在△EQF和△EPD中,
,
∴△EQF≌△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2中,在Rt△ABC中,AC=AB=2,
∵CE=,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,
∴四边形DECG是正方形,
∴CG=CE=.
20.证明:(1)①∵四边形ABCD是正方形,
∴∠ADB=∠CDB=45°,AD=DC,
在△ADH和△CDH中,
,
∴△ADH≌△CDH(SAS),
∴∠DAH=∠DCH;
②结论:EF=2CG,理由如下:
∵△DAH≌△DCH,
∴∠DAF=∠DCH,
∵CG⊥HC,
∴∠FCG+∠DCH=90°,
∴∠FCG+∠DAF=90°,
∵∠DFA+∠DAF=90°,∠DFA=∠CFG,
∴∠CFG=∠FCG,
∴GF=GC,
∵∠GCE+∠GCF=90°,∠CFG+∠E=90°,
∴∠GCE=∠GCF,
∴CG=GE,
∴EF=2CG;
(2)①如图,当点F在线段CD上时,连接DE.
∵∠GFC=∠GCF,∠GEC+∠GFC=90°,∠GCF+∠GCE=90°,
∴∠GCE=∠GEC,
∴EG=GC=FG,
∵FG=GE,FM=MD,
∴DE=2MG=8,
在Rt△DCE中,CE===2,
∴BE=BC+CE=6+2;
②如图,当点F在线段DC的延长线上时,连接DE.
同法可知GM是△DEC的中位线,
∴DE=2GM=6,
在Rt△DCE中,CE=2,
∴BE=BC﹣CE=6﹣2
综上所述,BE的长为 6+2或6﹣2.
21.(1)证明:∵点O是正方形对角线交点,
∴OB=OC,∠OBE=∠OCF=45°,
在△EBO和△FCO中,
,
∴△EBO≌△FCO(SAS),
∴OE=OF,
(2)解:由(1)可知,△EBO≌△FCO,
∴∠BOE=∠COF,
∵∠BOF+∠COF=∠BOE+∠COF=90°,
∴∠EOF=90°,
∵OE=OF,OG⊥EF,
∴OG垂直平分EF,OG平分∠EOF,
∴∠EOG=45°,
(3)解:∵OG垂直平分EF,
∴EG=GF,
∴△BEG的周长为BE+EG+BG=CF+GF+BG=BC,
∵BC=AB=10,
∴△BEG的周长为10,
(4)∵AC==10,
∴AO=AC=5,
∵AE=AO,
∴BE=AB﹣AE=10﹣5,
在△AED中,∠AOE=(180°﹣∠EAO)=67.5°,
∴∠BOE=∠AOB﹣∠AOE=22.5°,
∴∠BOG=∠EOG﹣∠BOE=22.5°,
∴OB为∠EOG的角平分线,
∵BO为∠EBG的角平分线,
∴∠OBG=∠OBE,
∴△OBG≌△OBE(ASA),
∴BE=BG,OE=OG,
∴OB⊥EG,
在△EBG中,EG==10﹣10,
∴S四边形BEOG=2S△OBG=×EG OB=50﹣25.
一.选择题(共8小题,满分40分)
1.如图,在正方形ABCD中,AB=4,点E在对角线AC上,若S△ABE=5,则△CDE的面积为( )
A.3 B.4 C.5 D.6
2.如图,在边长为4的正方形ABCD中,点E、点F分别是BC、AB上的点,连接DE、DF、EF,满足∠DEF=∠DEC.若AF=1,则EF的长为( )
A.2.4 B.3.4 C. D.
3.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(0,2),点B的坐标为(﹣3,0),则点C到y轴的距离是( )
A.6 B.5 C.4 D.3
4.如图,在正方形ABCD中,点E在对角线AC上,EF⊥AB于点F,EG⊥BC于点G,连接DE,若AB=10,AE=3,则ED的长度为( )
A.7 B.2 C. D.
5.如图,在正方形ABCD中,动点E在BC边上(点E与点B不重合),∠DAE的平分线AF与CD边交于点M,与BC边的延长线交于点F,连接EM.对于下列四个结论:①AE=EF;②若CM=CE,则AF=2BC;③若EM⊥AF,则CM=DM;④存在点E,使点E与点D关于直线AF对称.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
6.如图所示,O为正方形ABCD的中点,BE平分∠DBC,交DC于点E,延长BC到F,使FC=EC,连结DF交B的延长线于点H,连结OH交DC于点G,连结HC,则下列结论:①OH∥BF;②∠CHF=45°;③GH=BC;④三角形BDF是直角三角形.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
7.如图,点E在正方形ABCD的对角线AC上,且EC=AE,Rt△FEG的两直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD边长为4,则重叠部分四边形EMCN的面积为( )
A.2 B.4 C.6 D.8
8.如图,正方形ABCO和正方形DEFO的顶点A,O,E在同一直线l上,且EF=,AB=3,给出下列结论:①∠COD=45°;②AE=6;③CF=BD=;④△COF的面积是.其中正确的结论为( )
A.①③ B.①④ C.②③ D.①③④
二.填空题(共8小题,满分40分)
9.如图,点E,F在正方形ABCD的对角线AC上,AC=10,AE=CF=3,则四边形BFDE的面积为 .
10.如图,两个正方形边长分别为2、a(a>2),图中阴影部分的面积为 .
11.如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的度数是 度.
12.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为 .
13.如图,在正方形ABCD中,,E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN.则MN的长为 .
14.如图,已知正方形ABCD的边长为6,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=2,则FM的长为 .
15.如图,AD是△ABC的高,∠BAC=45°,若BD=10,DC=3,则高AD的长度为 .
16.如图,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,DE=10,则AD的长为 .
三.解答题(共5小题,满分40分)
17.如图,矩形ABCD对角线AC,BD相交于O,OE⊥BC,垂足为E.
(1)求证:OE=CD;
(2)若点F是OD的中点,连接EF交OC于点G,连接AF.
①求证:GE=GF.
②若AF=EF,求证:四边形ABCD是正方形.
18.已知:如图,四边形ABCD是菱形,点E,F分别在边BC,CD上,且BE=DF,过点F作AE的平行线交对角线AC的延长线于点G,连接EG.
(1)求证:四边形AEGF是菱形;
(2)如果∠B=∠BAE=30°,求证:四边形AEGF是正方形.
19.如图,四边形ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度.
20.已知正方形ABCD,点F是射线DC上一动点(不与C、D重合),连接AF并延长交直线BC于点E,交BD于点H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想线段CG与EF的关系并说明理由;
(2)取DF中点M,连结MG,若MG=4,正方形边长为6,求BE的长.
21.如图所示,在正方形ABCD中,AB=10,点O为对角线交点,BE=CF,连接EF,过点O作OG⊥EF交BC边于G,点G始终在BC边上,并且不与点B、点C重合,连接OE、OF、EG.
(1)求证:OE=OF;
(2)请求出∠EOG的度数?
(3)试求出△BEG的周长;
(4)若AE=AO,请直接写出四边形BEOG的面积.
参考答案
一.选择题(共8小题,满分40分)
1.解:过点E作MN∥AD,交AB于点M,CD于点N,
∵四边形ABCD是正方形,
∴AD⊥AB,AD⊥CD,AB=BC=CD=DA=4,
∵MN∥AD,
∴MN⊥AB,MN⊥CD,
∵S△ABE=AB EM=×4×EM=2EM=5,
∴EM=,
∴EN=AD﹣EM=AB﹣EM=4﹣=,
∴S△CDE=CD EN=×4×=3,
故选:A.
2.解:如图,在EF上截取EG=EC,连接DG,
∵四边形ABCD是正方形,
∴∠A=∠C=90°,AB=BC=4,
在△DCE和△DGE中,
,
∴△DCE≌△DGE(SAS),
∴∠DGE=∠C=90°,DG=DC,
∵∠A=∠C=90°,AB=BC=4,
∴∠DGF=∠A=90°,DG=DA,
在Rt△DAF和Rt△DGF中,
,
∴Rt△DAF≌Rt△DGF(HL),
∴AF=GF=1,
∵EG=EC,
∴BE=BC﹣EC=4﹣EG,EF=EG+FG=EG+1,BF=AB﹣AF=4﹣1=3,
在Rt△BEF中,根据勾股定理,得
BE2+BF2=EF2,
∴(4﹣EG)2+32=(EG+1)2,
解得EG=2.4,
∴EF=EG+FG=2.4+1=3.4.
∴EF的长为3.4.
故选:B.
3.解:过点C作CE⊥x轴于点E,如图,
则点C到y轴的距离为OE.
∵点A的坐标为(0,2),点B的坐标为(﹣3,0),
∴OA=2,OB=3.
∵CE⊥x轴,
∴∠CEB=90°.
∴∠ECB+∠EBC=90°.
∵四边形ABCD是正方形,
∴BC=AB,∠CBA=90°.
∴∠EBC+∠ABO=90°.
∴∠ECB=∠ABO.
在△CBE和△BAO中,
,
∴△CBE≌△BAO(AAS).
∴EB=OA=2.
∴OE=OB+BE=3+2=5.
∴点C到y轴的距离是5.
故选:B.
4.解:如图,连接BE,
∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,AB=AD,
∵AE=AE,
∴△ABE≌△ADE(SAS),
∴BE=DE,
∵EF⊥AB于点F,AE=3,
∴AF=EF=3,
∵AB=10,
∴BF=7,
∴BE==,
∴ED=.
故选:C.
5.解:∵AF平分∠DAE,
∴∠DAF=∠EAF,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAF=∠EFA,
∴∠EFA=∠EAF,
∴AE=EF,故①正确;
若CM=CE,
则DM=BE,
∵∠B=∠D=90°,AB=AD,
在△ABE和△ADM中,
,
∴△ABE≌△ADM(SAS),
∴∠BAE=∠DAM=∠EAF=30°,
∴∠F=30°,
∴AF=2AB,
∴AF=2BC,故②正确;
若EM⊥AF,
∴M是AF的中点,
∴AM=FM,
在△ADM和△FMC中,
,
∴△ADM≌△FMC(AAS),
∴CM=DM,故③正确;
只有当点E和点D重合时,
才有点E与点D关于直线AF对称.
与题意不符,故④错误.
综上所述:其中正确结论有①②③,共3个,
故选:C.
6.解:∵四边形ABCD是正方形,
∴∠BDC=∠DBC=45°,∠BCE=∠DCF=90°,BC=DC,
∵EC=FC,
∴△BCE≌△DCF(SAS),
∴∠EBC=∠FDC,∠BEC=∠F,
∵BE平分∠DBC,
∴∠DBH=∠FBH=∠FDC=22.5°,
∴∠BDF=∠BDC+∠FDC=45°+22.5°=67.5°,∠F=∠BEC=90°﹣∠EBC=90°﹣22.5°=67.5°,故④错误,不符合题意;
∴∠BDF=∠F,
∴BD=BF,△BDF是等腰三角形,
∴DH=HF,即点H是DF的中点,
∴CH=HF,
∴∠HCF=∠F=67.5°,
∴∠CHF=180°﹣∠HCF﹣∠F=45°,故②正确,符合题意;
∵O为BD的中点,
∴OH是三角形BDF的中位线,
∴OH∥BF,故①正确,符合题意;
∴GH=CF,
在正方形ABCD中,BD=BC,
∴BC=BD,
∵BF=BD,CF=BF﹣BC,
∴CF=BD﹣BD=BD,
∴GH=BD=×BC=BC,故③错误,不符合题意;
∴正确的有①②两个,
故选:B.
7.解:连接ED,
∵AE=EC,
∴点E是AC的中点,
∵四边形ABCD是正方形,
∴∠DEC=90°,DE=EC,∠EDN=∠ECM=45°,
∴∠DEN+∠NEC=90°,
∵EF⊥EG,
∴∠MEC+∠NEC=90°,
∴∠DEN=∠CEM,
∴△MEC≌△NED(ASA),
∴S△MEC=S△NED,
∴S四边形EMCN=S△MEC+S△NEC=S△NED+S△NEC=S△DEC,
∵正方形ABCD的边长为4,
∴AC=4,
∴ED=EC=2,
∴S△DEC==×2×2=4,
∴重叠部分四边形EMCN的面积为4.
故选:B.
8.解:①∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,
故正确;
②∵EF=,
∴OE=2,
∵AO=AB=3,
∴AE=AO+OE=2+3=5,
故错误;
③作DH⊥AB于H,作FG⊥CO交CO的延长线于G,
则FG=1,
CF===,
BH=3﹣1=2,
DH=3+1=4,
BD===2,
故错误;
④△COF的面积S△COF=×3×1=,
故正确;
∴其中正确的结论为①④,
故选:B.
二.填空题(共8小题,满分40分)
9.解:连接BD交AC于点O,
∵四边形ABCD为正方形,
∴OA=OB=OC=OD,AC⊥BD,
又∵AE=CF,
∴OE=OF,
∴四边形BEDF为平行四边形,
∵EF垂直平分BD,
∴EB=ED,
∴四边形BEDF是菱形,
∴BD=AC=10,
∵AE=CF=3,
∴EF=4,
∴四边形BFDE的面积为BD EF=×10×4=20.
故答案为:20.
10.解:阴影部分的面积=
11.解:∵四边形ABCD是正方形,
∴AB=BC=AD=CD,∠ABC=90°,∠ADG=∠CDG,∠ABD=45°,
∵GD=GD,
∴△ADG≌△CDG,
∴∠AGD=∠CGD,
∵∠CGD=∠EGB,
∴∠AGD=∠EGB,
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,
∴BE=BC,∠EBC=150°,
∴∠BEC=∠ECB=15°,
∴∠BGE=180°﹣∠BEC﹣∠EBG=180°﹣15°﹣60°﹣45°=60°,
∴∠AGD=60°
故答案为60.
12.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∴AB2=4,
∴AB=2,
故答案为:2.
13.解:连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴AB=CD=BC=2,AB∥CD,∠C=90°,
∴∠AEM=∠GDM,∠EAM=∠DGM,
∵M为DE的中点,
∴ME=MD,
在△AEM和GDM中,
,
∴△AEM≌△GDM(AAS),
∴AM=MG,AE=DG=AB=CD,
∴CG=CD=,
∵点N为AF的中点,
∴MN=FG,
∵F为BC的中点,
∴CF=BC=,
∴FG==2,
∴MN=1,
故答案为:1.
14.解:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
,
∴△DEF≌△DMF(SAS),
∴EF=MF,
设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
∴FM=5.
故答案为:5.
15.解:以AD为边作正方形ADEF,在EF上截取FQ=BD=10.
在△ABD和△AQF中,
,
∴△ABD≌△AQF(SAS),
∴AB=AQ,∠BAD=∠FAQ,
∵∠BAC=45°,
∴∠BAD+∠DAC=45°,
∴∠DAC+∠FAQ=45°,
即∠CAQ=45°,
∴∠BAC=∠CAQ.
在△BAC和△QAC中,
,
∴△BAC≌△QAC(SAS),
∴BC=CQ=BD+CD=13.
设AD=x,则QE=x﹣10,CE=x﹣3.
在Rt△CQE中,∠E=90°,
∵CE2+QE2=CQ2,
∴(x﹣3)2+(x﹣10)2=132,
解得:x1=15,x2=﹣2(不合舍去),
∴AD=15.
故答案为:15.
16.解:过C作CG⊥AD于G,并延长DG,使GF=BE,
在直角梯形ABCD中∵AD∥BC,∠A=∠B=90°,∠CGA=90°,AB=BC,
∴四边形ABCG为正方形,
∴AG=BC=12,
∵∠DCE=45°,
∵CE=CF,∠DCF=∠DCE,DC=DC,
∴△ECD≌△FCD(SAS).
∴ED=DF=10,
∴DE=DF+DG=BE+GD,
设AD=x,则DG=12﹣x,
∴AE=14﹣x,
在Rt△AED中,∵DE2=AD2+AE2,
∴102=(14﹣x)2+x2
∴x=8,x=6
即AD=8或6.
故答案为:8或6.
三.解答题(共5小题,满分40分)
17.(1)证明:∵矩形ABCD对角线AC,BD相交于O,
∴O是BD的中点,
∵OE⊥BC,DC⊥BC,
∴OE∥DC,
∴E是BC的中点,
∴OE是△BCD的中位线,
∴OE=CD;
(2)①证明:如图,取OB的中点H,连接EH,
∵点E是BC边的中点,
∴EH∥OC,
∴=,
∵四边形ABCD为矩形,
∴OB=OD,
∵点F是线段OD的中点,
∴OF=OH,
∴GE=GF;
②证明:如图,过点F作FM⊥BC于M,连接FC,
∵OB=OC,
∵点E是BC边的中点,
∴OE⊥BC,
∴OE∥FM∥CD,
∵点F是线段OD的中点,
∴点M是线段EC的中点,
∴FE=FC,
∵AF=FE,
∴AF=CF,
∵OA=OC,
∴OF所在直线是AC的垂直平分线,
∴DA=DC,
∴矩形ABCD为正方形.
18.(1)证明:∵菱形ABCD,
∴AB=AD,∠B=∠D,∠BAC=∠DAC,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,∠BAE=∠DAF,
∴∠EAG=∠FAG,
∵FG∥AE,
∴∠EAG=∠FGA,
∴∠FAG=∠FGA,
∴FG=AF=AE,
∵FG∥AE,
∴四边形AEGF是平行四边形,
又∵AF=AE,
∴四边形AEGF是菱形;
(2)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠B+∠BAD=180°,
∵∠B=∠BAE=30°,
∵△ABE≌△ADF,
∴∠BAE=∠DAF=30°,
∴∠BAD=180°﹣∠B=150°,
∴∠EAF=∠BAD﹣∠BAE﹣∠DAF=150°﹣30°﹣30°=90°,
∵四边形AEGF是菱形,
∴四边形AEGF是正方形.
19.(1)证明:如图1,作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED,
在△EQF和△EPD中,
,
∴△EQF≌△EPD(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2中,在Rt△ABC中,AC=AB=2,
∵CE=,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,
∴四边形DECG是正方形,
∴CG=CE=.
20.证明:(1)①∵四边形ABCD是正方形,
∴∠ADB=∠CDB=45°,AD=DC,
在△ADH和△CDH中,
,
∴△ADH≌△CDH(SAS),
∴∠DAH=∠DCH;
②结论:EF=2CG,理由如下:
∵△DAH≌△DCH,
∴∠DAF=∠DCH,
∵CG⊥HC,
∴∠FCG+∠DCH=90°,
∴∠FCG+∠DAF=90°,
∵∠DFA+∠DAF=90°,∠DFA=∠CFG,
∴∠CFG=∠FCG,
∴GF=GC,
∵∠GCE+∠GCF=90°,∠CFG+∠E=90°,
∴∠GCE=∠GCF,
∴CG=GE,
∴EF=2CG;
(2)①如图,当点F在线段CD上时,连接DE.
∵∠GFC=∠GCF,∠GEC+∠GFC=90°,∠GCF+∠GCE=90°,
∴∠GCE=∠GEC,
∴EG=GC=FG,
∵FG=GE,FM=MD,
∴DE=2MG=8,
在Rt△DCE中,CE===2,
∴BE=BC+CE=6+2;
②如图,当点F在线段DC的延长线上时,连接DE.
同法可知GM是△DEC的中位线,
∴DE=2GM=6,
在Rt△DCE中,CE=2,
∴BE=BC﹣CE=6﹣2
综上所述,BE的长为 6+2或6﹣2.
21.(1)证明:∵点O是正方形对角线交点,
∴OB=OC,∠OBE=∠OCF=45°,
在△EBO和△FCO中,
,
∴△EBO≌△FCO(SAS),
∴OE=OF,
(2)解:由(1)可知,△EBO≌△FCO,
∴∠BOE=∠COF,
∵∠BOF+∠COF=∠BOE+∠COF=90°,
∴∠EOF=90°,
∵OE=OF,OG⊥EF,
∴OG垂直平分EF,OG平分∠EOF,
∴∠EOG=45°,
(3)解:∵OG垂直平分EF,
∴EG=GF,
∴△BEG的周长为BE+EG+BG=CF+GF+BG=BC,
∵BC=AB=10,
∴△BEG的周长为10,
(4)∵AC==10,
∴AO=AC=5,
∵AE=AO,
∴BE=AB﹣AE=10﹣5,
在△AED中,∠AOE=(180°﹣∠EAO)=67.5°,
∴∠BOE=∠AOB﹣∠AOE=22.5°,
∴∠BOG=∠EOG﹣∠BOE=22.5°,
∴OB为∠EOG的角平分线,
∵BO为∠EBG的角平分线,
∴∠OBG=∠OBE,
∴△OBG≌△OBE(ASA),
∴BE=BG,OE=OG,
∴OB⊥EG,
在△EBG中,EG==10﹣10,
∴S四边形BEOG=2S△OBG=×EG OB=50﹣25.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
