8.2整式乘法练习题(安徽地区专用)2021-2022学年下学期安徽省各地沪科版七年级数学期中复习(Word版含答案)
文档属性
| 名称 | 8.2整式乘法练习题(安徽地区专用)2021-2022学年下学期安徽省各地沪科版七年级数学期中复习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 319.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 16:24:46 | ||
图片预览




文档简介
8.2整式乘法练习题
一、单选题
1.(2021·安徽·马鞍山八中七年级期中)已知,则的值是( )
A.-2 B.0 C.2 D.4
2.(2021·安徽合肥·七年级期中)若(x+8)(x-1)=x2+mx+n任意x都成立,则m+n=( )
A.-8 B.-1 C.1 D.8
3.(2021·安徽·淮南市田家庵区教育体育局教研室七年级期中)如图所示,一块“L”型菜地,小新在求菜地面积的面积时,列出了下列4个式子,其中错误的是( )
A. B.
C. D.
4.(2021·安徽·利辛县第四中学七年级期中)如果(x-2)(x+3)=x2+px+q,那么p、q的值是( )
A.p=5,q=6 B.p=1,q=6 C.p=5,q=-6 D.p=1,q=-6
5.(2021·安徽·安庆市第十四中学七年级期中)如果□×3ab=3a2b,那么□内应填的代数式是 ( )
A.ab B.3ab C.a D.3a
6.(2021·安徽·合肥市第四十五中学七年级期中)要使展开式中不含项,则的值等于( )
A. B. C. D.
7.(2021·安徽合肥·七年级期中)已知(x﹣2)(x2+mx+n)的乘积项中不含x2和x项,则m,n的值分别为( )
A.m=2,n=4 B.m=3,n=6 C.m=﹣2,n=﹣4 D.m=﹣3,n=﹣6
二、填空题
8.(2021·安徽·安庆市第十四中学七年级期中)若化简的结果中不含的一次项,则常数的值为______.
9.(2021·安徽合肥·七年级期中)如图,将从1开始的连续奇数按如图所示的规律排列,例如,位于第3行第4列的数为23,则位于第25行第11列的数是 .
10.(2021·安徽合肥·七年级期中)已知有甲、乙两个长方形,它们的边长如图所示(为正整数),面积分别为、.
(1)请比较与的大小:________.
(2)满足条件的整数有且只有4个,则________.
三、解答题
11.(2021·安徽·淮南市田家庵区教育体育局教研室七年级期中)先化简,再求值.,其中,.
12.(2021·安徽·利辛县第四中学七年级期中)先化简,再求值.,其中.
13.(2021·安徽·利辛县第四中学七年级期中)(1)计算:
;
;
猜想:;
(2)请你利用上式的结论,求的值;
(3)请直接写出的值.
14.(2021·安徽·安庆市第四中学七年级期中)观察下列等式:
第1个等式:12=13;
第2个等式:(1+2)2=13+23;
第3个等式:(1+2+3)2=13+23+33;
第4个等式:(1+2+3+4)2=13+23+33+43
……
按照以上规律,解决下列问题:
(1)写出第5个等式: ;
(2)写出第n(n为正整数)个等式: (用含n的等式表示);
(3)利用你发现的规律求113+123+133+…+1003值.
15.(2021·安徽合肥·七年级期中)观察下列各式:
①1×2-0×3=2;②2×3-1×4=2;③3×4-2×5=2;④4×5-3×6=2;……
(1)请按上述规律写出第⑤个式子:________;
(2)请按上述规律写出第n个等式(用含字母的式子表示);
(3)你认为(2)中所写的等式一定成立吗?请说明理由.
16.(2021·安徽合肥·七年级期中)芳芳计算一道整式乘法的题:(2x +m)(5x-4),由于芳芳将第一个多项式中的“+ m”抄成“-m”,得到的结果为10x2 - 33x + 20.
(1)求m的值;
(2)请解出这道题的正确结果.
17.(2021·安徽·合肥市第四十二中学七年级期中)在长方形ABCD内,将两张边长分别为a和b()的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为,图2中阴影部分的面积为,当时求的值(用含a、b的代数式表示).
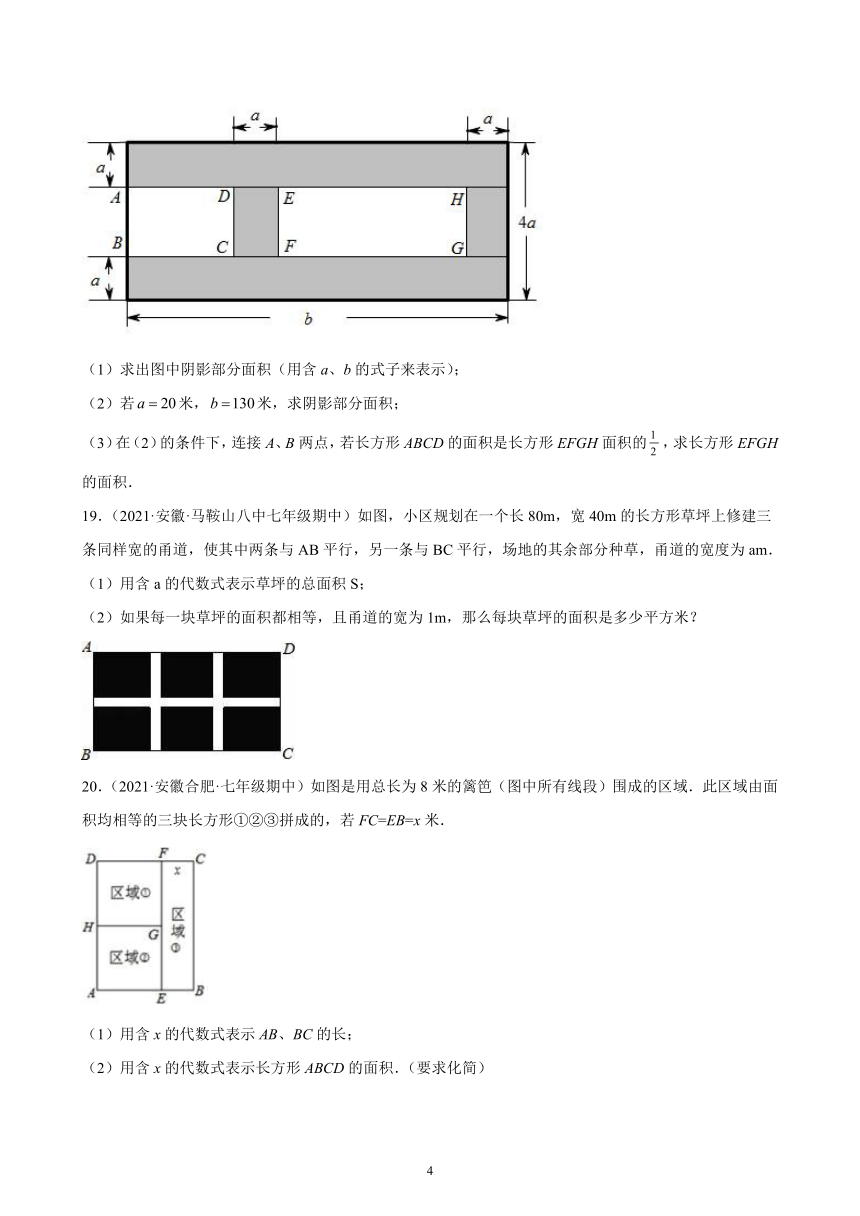
18.(2021·安徽·合肥市五十中学西校七年级期中)下图为某校教学楼的俯视图,根据图中信息,解决下列问题:
(1)求出图中阴影部分面积(用含a、b的式子来表示);
(2)若米,米,求阴影部分面积;
(3)在(2)的条件下,连接A、B两点,若长方形ABCD的面积是长方形EFGH面积的,求长方形EFGH的面积.
19.(2021·安徽·马鞍山八中七年级期中)如图,小区规划在一个长80m,宽40m的长方形草坪上修建三条同样宽的甬道,使其中两条与AB平行,另一条与BC平行,场地的其余部分种草,甬道的宽度为am.
(1)用含a的代数式表示草坪的总面积S;
(2)如果每一块草坪的面积都相等,且甬道的宽为1m,那么每块草坪的面积是多少平方米?
20.(2021·安徽合肥·七年级期中)如图是用总长为8米的篱笆(图中所有线段)围成的区域.此区域由面积均相等的三块长方形①②③拼成的,若FC=EB=x米.
(1)用含x的代数式表示AB、BC的长;
(2)用含x的代数式表示长方形ABCD的面积.(要求化简)
试卷第1页,共3页
参考答案:
1.B
【解析】
先根据,得到,再由即可得到答案.
解:∵,
∴
∴
,
故选B.
本题主要考查了整式的混合计算和代数式求值,解题的关键在于能够熟知相关计算法则和利用整体代入的思想求解.
2.B
【解析】
已知等式左边利用多项式乘多项式法则计算,根据多项式相等的条件即可求出、的值,相加即可求解.
解:,
,,
.
故选:.
此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
3.C
【解析】
题目主要考查利用代数式表示不规则图形的面积,根据题意,作出辅助线求解即可得.
解:A选项如图所示:将不规则图形分为两个长方形,
∴面积为:,A选项正确;
B选项如图所示:将不规则图形分为两个长方形,
面积为:,B选项正确;
D选项如图所示:将不规则图形补全,
面积为:,D选项正确;
C选项不能表示图形面积,错误;
故选:C.
题目主要考查利用代数式表示不规则图形的面积,理解题意,作出相应辅助线是解题关键.
4.D
【解析】
先根据多项式乘以多项式的法则,将(x-2)(x+3)展开,再根据两个多项式相等的条件即可确定p、q的值.
解:∵(x-2)(x+3)=x2+x-6,
又∵(x-2)(x+3)=x2+px+q,
∴x2+px+q=x2+x-6,
∴p=1,q=-6.
故选:D.
本题主要考查多项式乘以多项式的法则及两个多项式相等的条件.多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.两个多项式相等时,它们同类项的系数对应相等.
5.C
【解析】
已知积和其中一个因式,求另外一个因式,可用积除以已知因式,得所求因式.
解:∵3a2b÷3ab=a,
∴□=a.
故选C.
6.A
【解析】
根据多项式乘以多项式的法则进行展开,然后按照x的降序排列,使x的二次项的系数为0即可.
解:(x2-x+5)(2x2-ax-4)
=2x4-ax3-4x2-2x3+ax2+4x+10x2-5ax-20
=2x4-(a+2)x3+(a+6)x2+(4-5a)x-20,
∵展开式中不含x2项,
∴a+6=0,
∴a=-6,
故选:A.
本题考查多项式乘以多项式,掌握多项式乘以多项式的计算法则是正确解答的前提,令x的二次项的系数为0是正确解答的关键.
7.A
【解析】
先根据多项式的乘法法则计算,合并同类项后根据乘积项中不含x2和x项可得这两项的系数为0,进一步即可求出答案.
解:原式=x3+(m﹣2)x2+(n﹣2m)x﹣2n,
∵乘积项中不含x2和x项,
∴m﹣2=0,n﹣2m=0,
解得:m=2,n=4.
故选:A.
本题主要考查了多项式的乘法,属于常考题型,正确理解题意、熟练掌握多项式乘以多项式的运算法则是关键.
8.2021
【解析】
先用多项式乘以多项式的法则展开,然后合并同类项,不含x的一次项,就让x的一次项的系数等于0.
解:
=
=
∵不含的一次项,
∴,
∴.
故答案为:2021.
本题考查了多项式乘以多项式法则,考核学生的计算能力,解决这类问题的方法是:不含哪一项,就合并同类项后让这一项的系数等于0.
9.1173
【解析】
根据数字的变化关系发现规律第n行,第n列的数据为:2×n×(n-1)+1,即可得第25行第25列的数据为:1201,再依次减2,到第25行第11列的数据,即可.
解:第1行第1列的数是1,这里,
1=2×1×(1-1)+1,
第2行第2列的数是5,这里,
5=2×2×(2-1)+1,
第3行第3列的数是13,这里,
13=2×3×(3-1)+1,
第4行第4列的数是25,这里,
25=2×4×(4-1)+1,
……
∴第n行第n列的数是2×n×(n-1)+1,
第25行第25列的数是
2×25×(25-1)+1=50×24+1=1201,
观察数据的排列,发现排列规律:第奇数行从右往左的数据依次减少2,
第25行最右边的数是1201,这里,1201位于第25行第25列,
从第25列到第11列需要移动的列数为:25-11=14(列),
从右往左的数据每移动1列,数据就减少2,
∴第25行第11列的数是:
1201-14×2=1173.
故答案为:1173.
本题考查了数字的变化类,解决本题的关键是观察数字的变化寻找探究规律,利用规律解决问题.
10. > 2
【解析】
(1)根据矩形的面积公式计算出和,再求出差即可比较出大小;
(2)根据题意得出关于m的不等式,解之即可得到结论.
解:(1),
,
为正整数,
,
故答案为:;
(2)由(1)得,,
有4个整数解
这4个整数为5,6,7,8,
为正整数,
,
故答案为:2.
本题主要考查整式的混合运算、一元一次不等式的应用,解题的关键是掌握多项式乘多项式、矩形的性质、正方形的性质等知识.
11.,68
【解析】
先去括号,合并同类项,然后将已知值代入代数式求解即可.
解:
当,时,
原式,
,
.
题目主要考查整式的混合运算化简求值,熟练掌握整式的运算法则是解题关键.
12.,.
【解析】
先根据整式的混合运算计算法则化简,然后代值计算即可.
解:
,
当时,原式.
本题主要考查了整式的化简求值,解题的关键在于能够熟练掌握整式的混合运算计算法则.
13.(1);(2);(3).
【解析】
(1)根据多项式乘多项式可进行求解;
(2)由2-1=1及(1)中结论可直接进行求解;
(3)根据(1)中结论可进行求解.
解:(1)由题意得:
,
,
……
猜想:;
故答案为;
(2)由(1)可得:
原式=
(3)由(1)的结论可得:
原式=.
本题主要考查多项式乘多项式的应用,熟练掌握多项式乘多项式是解题的关键.
14.(1);(2);(3)25499475.
【解析】
(1)根据题干即可直接写出第5个等式.
(2)利用前几个等式可总结出规律:从1开始连续几个整数的和的平方等于这些数的立方的和”即可写出第n(n为正整数)个等式.
(3)根据,结合(2)总结的规律,可得:,即可求出结果.
(1)根据题干可知第5个等式为:.
(2)根据前面等式即可总结出规律,第n(n为正整数)个等式为:
(3) ,
.
本题考查多项式乘法中的规律性问题.根据题干总结出等式的规律是解答本题的关键.
15.(1)5×6-4×7=2;(2)n(n+1)-(n-1)(n+2)=2;(3)成立,理由见解析
【解析】
(1)观察各式,发现规律即可得到第⑤个式子;
(2)从特殊到一般,用表示出各式规律即可;
(3)根据整数的运算求证(2)中的等式即可.
解:(1)5×6-4×7=2;
(2)n(n+1)-(n-1)(n+2)=2;
(3)一定成立;理由如下:
n(n+1)-(n-1)(n+2)=n2+n-n2-2n+n+2=2
本题考查规律探究及整式乘法的混合运算,观察已知等式找到变化规律是关键.
16.(1)m=5;(2)
【解析】
(1)化简,根据一次项的系数和常数项即可求出m的值;
(2)将代入原式求解即可.
(1).
∴
解得
(2)将代入原式中
原式
.
本题考查了整式的运算问题,掌握整式混合运算法则是解题的关键.
17.
【解析】
设,则,根据图形得出,再根据整式的运算法则即可求出答案.
解:设,则,
本题考查了列代数式和整式的混合运算,解题的关键是:能灵活运用整式的运算法则进行计算.
18.(1)2ab+4a ;(2)6800平方米;(3)2400平方米.
【解析】
(1)观察图形很容易得出阴影部分的面积为4ab-(4a-2a)(b-2a),化简即可;
(2)把米,米,代入求解即可;
(3)根据长方形ABCD的面积是长方形EFGH面积的,列出关系式求解即可.
解:(1)根据图形可观察出:4ab-(4a-2a)(b-2a)=2ab+4a ;
(2)当米,米时,
阴影部分面积为:2ab+4a =2×20×130+4×20 =6800(平方米);
(3)长方形EFGH的面积为:(4a-2a)(b-2a)×=2400(平方米).
本题考查了列代数式及代数式求值,解题的关键是理解题意,找出等量关系.
19.(1)S=2a2﹣160a+3200;(2)每一块草坪的面积是507m2.
【解析】
试题分析:(1)利用平移思想,计算长方形的面积即可;
(2)把x=1代入(1)式求出数值即可.
解:(1)S=(80﹣2a)(40﹣a)=2a2﹣160a+3200;
(2)当a=1时,s=2×12﹣160×1+3200=3042m2
所以每一块草坪的面积为3042÷6=507m2
答:每一块草坪的面积是507m2.
考点:列代数式;代数式求值.
20.(1);(2)
【解析】
(1)根据长方形的性质即可得到AE=DF=HG=2x,DH=HA=GE=FG,根据线段的和差关系可用含x的代数式表示AB和BC的长度;
(2)根据长方形的面积公式求出答案即可
(1)解: 根据题意可得,AE=DF=GH=2x,DH=HA=GE=FG
∴AB=2x+x=3x
BC=AD=EF=;
(2)解: S长方形ABCD=AB×BC=3x×=8x-8x2
本题主要考查了列式表示数量关系,长方形的面积公式,解题的关键在于能够熟练掌握相关知识进行求解.
答案第1页,共2页
一、单选题
1.(2021·安徽·马鞍山八中七年级期中)已知,则的值是( )
A.-2 B.0 C.2 D.4
2.(2021·安徽合肥·七年级期中)若(x+8)(x-1)=x2+mx+n任意x都成立,则m+n=( )
A.-8 B.-1 C.1 D.8
3.(2021·安徽·淮南市田家庵区教育体育局教研室七年级期中)如图所示,一块“L”型菜地,小新在求菜地面积的面积时,列出了下列4个式子,其中错误的是( )
A. B.
C. D.
4.(2021·安徽·利辛县第四中学七年级期中)如果(x-2)(x+3)=x2+px+q,那么p、q的值是( )
A.p=5,q=6 B.p=1,q=6 C.p=5,q=-6 D.p=1,q=-6
5.(2021·安徽·安庆市第十四中学七年级期中)如果□×3ab=3a2b,那么□内应填的代数式是 ( )
A.ab B.3ab C.a D.3a
6.(2021·安徽·合肥市第四十五中学七年级期中)要使展开式中不含项,则的值等于( )
A. B. C. D.
7.(2021·安徽合肥·七年级期中)已知(x﹣2)(x2+mx+n)的乘积项中不含x2和x项,则m,n的值分别为( )
A.m=2,n=4 B.m=3,n=6 C.m=﹣2,n=﹣4 D.m=﹣3,n=﹣6
二、填空题
8.(2021·安徽·安庆市第十四中学七年级期中)若化简的结果中不含的一次项,则常数的值为______.
9.(2021·安徽合肥·七年级期中)如图,将从1开始的连续奇数按如图所示的规律排列,例如,位于第3行第4列的数为23,则位于第25行第11列的数是 .
10.(2021·安徽合肥·七年级期中)已知有甲、乙两个长方形,它们的边长如图所示(为正整数),面积分别为、.
(1)请比较与的大小:________.
(2)满足条件的整数有且只有4个,则________.
三、解答题
11.(2021·安徽·淮南市田家庵区教育体育局教研室七年级期中)先化简,再求值.,其中,.
12.(2021·安徽·利辛县第四中学七年级期中)先化简,再求值.,其中.
13.(2021·安徽·利辛县第四中学七年级期中)(1)计算:
;
;
猜想:;
(2)请你利用上式的结论,求的值;
(3)请直接写出的值.
14.(2021·安徽·安庆市第四中学七年级期中)观察下列等式:
第1个等式:12=13;
第2个等式:(1+2)2=13+23;
第3个等式:(1+2+3)2=13+23+33;
第4个等式:(1+2+3+4)2=13+23+33+43
……
按照以上规律,解决下列问题:
(1)写出第5个等式: ;
(2)写出第n(n为正整数)个等式: (用含n的等式表示);
(3)利用你发现的规律求113+123+133+…+1003值.
15.(2021·安徽合肥·七年级期中)观察下列各式:
①1×2-0×3=2;②2×3-1×4=2;③3×4-2×5=2;④4×5-3×6=2;……
(1)请按上述规律写出第⑤个式子:________;
(2)请按上述规律写出第n个等式(用含字母的式子表示);
(3)你认为(2)中所写的等式一定成立吗?请说明理由.
16.(2021·安徽合肥·七年级期中)芳芳计算一道整式乘法的题:(2x +m)(5x-4),由于芳芳将第一个多项式中的“+ m”抄成“-m”,得到的结果为10x2 - 33x + 20.
(1)求m的值;
(2)请解出这道题的正确结果.
17.(2021·安徽·合肥市第四十二中学七年级期中)在长方形ABCD内,将两张边长分别为a和b()的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为,图2中阴影部分的面积为,当时求的值(用含a、b的代数式表示).
18.(2021·安徽·合肥市五十中学西校七年级期中)下图为某校教学楼的俯视图,根据图中信息,解决下列问题:
(1)求出图中阴影部分面积(用含a、b的式子来表示);
(2)若米,米,求阴影部分面积;
(3)在(2)的条件下,连接A、B两点,若长方形ABCD的面积是长方形EFGH面积的,求长方形EFGH的面积.
19.(2021·安徽·马鞍山八中七年级期中)如图,小区规划在一个长80m,宽40m的长方形草坪上修建三条同样宽的甬道,使其中两条与AB平行,另一条与BC平行,场地的其余部分种草,甬道的宽度为am.
(1)用含a的代数式表示草坪的总面积S;
(2)如果每一块草坪的面积都相等,且甬道的宽为1m,那么每块草坪的面积是多少平方米?
20.(2021·安徽合肥·七年级期中)如图是用总长为8米的篱笆(图中所有线段)围成的区域.此区域由面积均相等的三块长方形①②③拼成的,若FC=EB=x米.
(1)用含x的代数式表示AB、BC的长;
(2)用含x的代数式表示长方形ABCD的面积.(要求化简)
试卷第1页,共3页
参考答案:
1.B
【解析】
先根据,得到,再由即可得到答案.
解:∵,
∴
∴
,
故选B.
本题主要考查了整式的混合计算和代数式求值,解题的关键在于能够熟知相关计算法则和利用整体代入的思想求解.
2.B
【解析】
已知等式左边利用多项式乘多项式法则计算,根据多项式相等的条件即可求出、的值,相加即可求解.
解:,
,,
.
故选:.
此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
3.C
【解析】
题目主要考查利用代数式表示不规则图形的面积,根据题意,作出辅助线求解即可得.
解:A选项如图所示:将不规则图形分为两个长方形,
∴面积为:,A选项正确;
B选项如图所示:将不规则图形分为两个长方形,
面积为:,B选项正确;
D选项如图所示:将不规则图形补全,
面积为:,D选项正确;
C选项不能表示图形面积,错误;
故选:C.
题目主要考查利用代数式表示不规则图形的面积,理解题意,作出相应辅助线是解题关键.
4.D
【解析】
先根据多项式乘以多项式的法则,将(x-2)(x+3)展开,再根据两个多项式相等的条件即可确定p、q的值.
解:∵(x-2)(x+3)=x2+x-6,
又∵(x-2)(x+3)=x2+px+q,
∴x2+px+q=x2+x-6,
∴p=1,q=-6.
故选:D.
本题主要考查多项式乘以多项式的法则及两个多项式相等的条件.多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.两个多项式相等时,它们同类项的系数对应相等.
5.C
【解析】
已知积和其中一个因式,求另外一个因式,可用积除以已知因式,得所求因式.
解:∵3a2b÷3ab=a,
∴□=a.
故选C.
6.A
【解析】
根据多项式乘以多项式的法则进行展开,然后按照x的降序排列,使x的二次项的系数为0即可.
解:(x2-x+5)(2x2-ax-4)
=2x4-ax3-4x2-2x3+ax2+4x+10x2-5ax-20
=2x4-(a+2)x3+(a+6)x2+(4-5a)x-20,
∵展开式中不含x2项,
∴a+6=0,
∴a=-6,
故选:A.
本题考查多项式乘以多项式,掌握多项式乘以多项式的计算法则是正确解答的前提,令x的二次项的系数为0是正确解答的关键.
7.A
【解析】
先根据多项式的乘法法则计算,合并同类项后根据乘积项中不含x2和x项可得这两项的系数为0,进一步即可求出答案.
解:原式=x3+(m﹣2)x2+(n﹣2m)x﹣2n,
∵乘积项中不含x2和x项,
∴m﹣2=0,n﹣2m=0,
解得:m=2,n=4.
故选:A.
本题主要考查了多项式的乘法,属于常考题型,正确理解题意、熟练掌握多项式乘以多项式的运算法则是关键.
8.2021
【解析】
先用多项式乘以多项式的法则展开,然后合并同类项,不含x的一次项,就让x的一次项的系数等于0.
解:
=
=
∵不含的一次项,
∴,
∴.
故答案为:2021.
本题考查了多项式乘以多项式法则,考核学生的计算能力,解决这类问题的方法是:不含哪一项,就合并同类项后让这一项的系数等于0.
9.1173
【解析】
根据数字的变化关系发现规律第n行,第n列的数据为:2×n×(n-1)+1,即可得第25行第25列的数据为:1201,再依次减2,到第25行第11列的数据,即可.
解:第1行第1列的数是1,这里,
1=2×1×(1-1)+1,
第2行第2列的数是5,这里,
5=2×2×(2-1)+1,
第3行第3列的数是13,这里,
13=2×3×(3-1)+1,
第4行第4列的数是25,这里,
25=2×4×(4-1)+1,
……
∴第n行第n列的数是2×n×(n-1)+1,
第25行第25列的数是
2×25×(25-1)+1=50×24+1=1201,
观察数据的排列,发现排列规律:第奇数行从右往左的数据依次减少2,
第25行最右边的数是1201,这里,1201位于第25行第25列,
从第25列到第11列需要移动的列数为:25-11=14(列),
从右往左的数据每移动1列,数据就减少2,
∴第25行第11列的数是:
1201-14×2=1173.
故答案为:1173.
本题考查了数字的变化类,解决本题的关键是观察数字的变化寻找探究规律,利用规律解决问题.
10. > 2
【解析】
(1)根据矩形的面积公式计算出和,再求出差即可比较出大小;
(2)根据题意得出关于m的不等式,解之即可得到结论.
解:(1),
,
为正整数,
,
故答案为:;
(2)由(1)得,,
有4个整数解
这4个整数为5,6,7,8,
为正整数,
,
故答案为:2.
本题主要考查整式的混合运算、一元一次不等式的应用,解题的关键是掌握多项式乘多项式、矩形的性质、正方形的性质等知识.
11.,68
【解析】
先去括号,合并同类项,然后将已知值代入代数式求解即可.
解:
当,时,
原式,
,
.
题目主要考查整式的混合运算化简求值,熟练掌握整式的运算法则是解题关键.
12.,.
【解析】
先根据整式的混合运算计算法则化简,然后代值计算即可.
解:
,
当时,原式.
本题主要考查了整式的化简求值,解题的关键在于能够熟练掌握整式的混合运算计算法则.
13.(1);(2);(3).
【解析】
(1)根据多项式乘多项式可进行求解;
(2)由2-1=1及(1)中结论可直接进行求解;
(3)根据(1)中结论可进行求解.
解:(1)由题意得:
,
,
……
猜想:;
故答案为;
(2)由(1)可得:
原式=
(3)由(1)的结论可得:
原式=.
本题主要考查多项式乘多项式的应用,熟练掌握多项式乘多项式是解题的关键.
14.(1);(2);(3)25499475.
【解析】
(1)根据题干即可直接写出第5个等式.
(2)利用前几个等式可总结出规律:从1开始连续几个整数的和的平方等于这些数的立方的和”即可写出第n(n为正整数)个等式.
(3)根据,结合(2)总结的规律,可得:,即可求出结果.
(1)根据题干可知第5个等式为:.
(2)根据前面等式即可总结出规律,第n(n为正整数)个等式为:
(3) ,
.
本题考查多项式乘法中的规律性问题.根据题干总结出等式的规律是解答本题的关键.
15.(1)5×6-4×7=2;(2)n(n+1)-(n-1)(n+2)=2;(3)成立,理由见解析
【解析】
(1)观察各式,发现规律即可得到第⑤个式子;
(2)从特殊到一般,用表示出各式规律即可;
(3)根据整数的运算求证(2)中的等式即可.
解:(1)5×6-4×7=2;
(2)n(n+1)-(n-1)(n+2)=2;
(3)一定成立;理由如下:
n(n+1)-(n-1)(n+2)=n2+n-n2-2n+n+2=2
本题考查规律探究及整式乘法的混合运算,观察已知等式找到变化规律是关键.
16.(1)m=5;(2)
【解析】
(1)化简,根据一次项的系数和常数项即可求出m的值;
(2)将代入原式求解即可.
(1).
∴
解得
(2)将代入原式中
原式
.
本题考查了整式的运算问题,掌握整式混合运算法则是解题的关键.
17.
【解析】
设,则,根据图形得出,再根据整式的运算法则即可求出答案.
解:设,则,
本题考查了列代数式和整式的混合运算,解题的关键是:能灵活运用整式的运算法则进行计算.
18.(1)2ab+4a ;(2)6800平方米;(3)2400平方米.
【解析】
(1)观察图形很容易得出阴影部分的面积为4ab-(4a-2a)(b-2a),化简即可;
(2)把米,米,代入求解即可;
(3)根据长方形ABCD的面积是长方形EFGH面积的,列出关系式求解即可.
解:(1)根据图形可观察出:4ab-(4a-2a)(b-2a)=2ab+4a ;
(2)当米,米时,
阴影部分面积为:2ab+4a =2×20×130+4×20 =6800(平方米);
(3)长方形EFGH的面积为:(4a-2a)(b-2a)×=2400(平方米).
本题考查了列代数式及代数式求值,解题的关键是理解题意,找出等量关系.
19.(1)S=2a2﹣160a+3200;(2)每一块草坪的面积是507m2.
【解析】
试题分析:(1)利用平移思想,计算长方形的面积即可;
(2)把x=1代入(1)式求出数值即可.
解:(1)S=(80﹣2a)(40﹣a)=2a2﹣160a+3200;
(2)当a=1时,s=2×12﹣160×1+3200=3042m2
所以每一块草坪的面积为3042÷6=507m2
答:每一块草坪的面积是507m2.
考点:列代数式;代数式求值.
20.(1);(2)
【解析】
(1)根据长方形的性质即可得到AE=DF=HG=2x,DH=HA=GE=FG,根据线段的和差关系可用含x的代数式表示AB和BC的长度;
(2)根据长方形的面积公式求出答案即可
(1)解: 根据题意可得,AE=DF=GH=2x,DH=HA=GE=FG
∴AB=2x+x=3x
BC=AD=EF=;
(2)解: S长方形ABCD=AB×BC=3x×=8x-8x2
本题主要考查了列式表示数量关系,长方形的面积公式,解题的关键在于能够熟练掌握相关知识进行求解.
答案第1页,共2页
同课章节目录
