2021-2022学年鲁教版(五四制)六年级数学下册6.7完全平方公式同步优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学下册6.7完全平方公式同步优生辅导训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 67.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版六年级数学下册《6-7完全平方公式》同步优生辅导训练(附答案)
一.选择题
1.下列计算正确的是( )
A.(2a+b)2=4a2+b2
B.(5x﹣2y)2=25x2﹣10xy+4y2
C.(x﹣y)2=x2﹣xy+y2
D.(x+)2=x2+x+
2.已知(x﹣2020)2+(x﹣2022)2=18,则(x﹣2021)2的值是( )
A.4 B.8 C.12 D.16
3.若x2+2mx+16是完全平方式,则(m﹣1)2+2的值是( )
A.11 B.3 C.11或27 D.3或11
4.若9x2﹣(K﹣1)x+1是关于x的完全平方式,则常数K的值为( )
A.0 B.﹣5或7 C.7 D.9
5.如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为56,面积之和为58,则长方形ABCD的面积为( )
A.98 B.49 C.20 D.10
6.将四个长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=2S2,则a,b满足( )
A.a=2b B.a=3b C.2a=3b D.2a=5b
二.填空题
7.若a﹣b=5,ab=3,则a2+b2= .
8.多项式x2+2mx+64是完全平方式,则m= .
9.已知x+=3,那么= .
10.若a+b=8,ab=﹣5,则(a﹣b)2= .
11.如图,有三种卡片,其中边长为a的正方形卡片4张,边长分别为a、b的矩形卡片12张,边长为b的正方形卡片9张.用这25张卡片拼成一个正方形,则这个正方形的边长为 .
12.已知a+b=3,ab=﹣1,则a2+ab+b2= .
13.已知a+10=b+12=c+15,则a2+b2+c2﹣ab﹣bc﹣ac= .
14.已知a+b=8,ab=12,则﹣ab= .
三.解答题
15.已知x+y=7,xy=﹣8,求
(1)x2+y2的值; (2)(x﹣y)2的值.
16.已知(a+b)2=5,(a﹣b)2=3,求下列式子的值:
(1)a2+b2; (2)6ab.
17.如图,将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形.
(1)若用不同的方法计算这个边长为(a+b+c)的正方形面积,就可以得到一个等式,这个等式可以为 (只要写出一个即可);
(2)请利用(1)中的等式解答下列问题:
①若三个实数a,b,c满足a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
②若三个实数x,y,z满足2x×4y÷8z=,x2+4y2+9z2=44,求2xy﹣3xz﹣6yz的值.
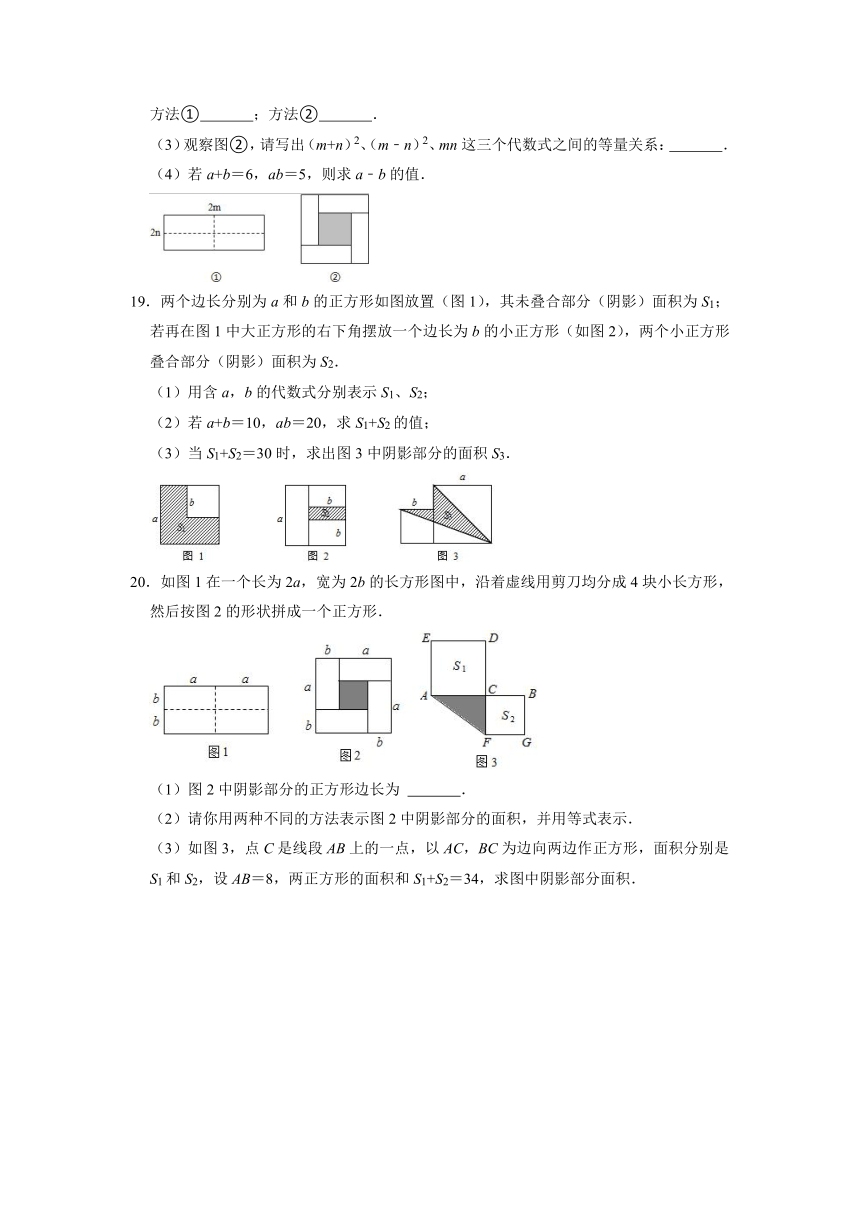
18.如图①所示是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)图②中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法表示图②中阴影部分的面积.
方法① ;方法② .
(3)观察图②,请写出(m+n)2、(m﹣n)2、mn这三个代数式之间的等量关系: .
(4)若a+b=6,ab=5,则求a﹣b的值.
19.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a,b的代数式分别表示S1、S2;
(2)若a+b=10,ab=20,求S1+S2的值;
(3)当S1+S2=30时,求出图3中阴影部分的面积S3.
20.如图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=34,求图中阴影部分面积.
参考答案
一.选择题
1.解:A、(2a+b)2=4a2+4ab+b2,原计算错误,故此选项不符合题意;
B、(5x﹣2y)2=25x2﹣20xy+4y2,原计算错误,故此选项不符合题意;
C、(x﹣y)2=x2﹣xy+y2,原计算错误,故此选项不符合题意误;
D、原计算正确,故此选项符合题意.
故选:D.
2.解:∵(x﹣2020)2+(x﹣2022)2=18,
∴[(x﹣2021)+1]2+[(x﹣2021)﹣1]2=18,
∴(x﹣2021)2+2(x﹣2021)+1+(x﹣2021)2﹣2(x﹣2021)+1=18,
∴(x﹣2021)2=8.
故选:B.
3.解:∵x2+2mx+16是完全平方式.
∴m2=16.
∴m=±4.
当m=4时,(m﹣1)2+2=9+2=11.
当m=﹣4时(m﹣1)2+2=25+2=27.
故答案为:C.
故选:C.
4.解:9x2﹣(K﹣1)x+1=(3x)2﹣(K﹣1)x+12.
∵9x2﹣(K﹣1)x+1是关于x的完全平方式,
∴9x2﹣(K﹣1)x+1=(3x)2±2 3x 1+12=(3x)2±6x+12.
∴﹣(K﹣1)=±6.
当﹣(K﹣1)=6时,K=﹣5.
当﹣(K﹣1)=﹣6时,K=7.
综上:K=﹣5或7.
故选:B.
5.解:设AB=DC=x,AD=BC=y,由题意得:
化简得:
将①两边平方再减去②得:2xy=20
∴xy=10
故选:D.
6.解:∵S1=2×b(a+b)+2×ab+2×(a﹣b)
=a2+2b2,
S2=(a+b)2﹣(a2+2b2)
=2ab﹣b2,
又∵S1=2S2,
∴a2+2b2=2(2ab﹣b2),
整理,得(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:A.
二.填空题
7.解:把a﹣b=5两边平方得:(a﹣b)2=a2+b2﹣2ab=25,
将ab=3代入得:a2+b2=31,
故答案为:31
8.解:∵x2+2mx+64是完全平方式,
∴2mx=±2 x 8,
∴m=±8.
9.解:∵x+=3,
∴x2+=(x+)2﹣2=7,
∴=(x2+)2﹣2=47.
10.解:把a+b=8两边平方得:(a+b)2=a2+b2+2ab=64,
将ab=﹣5代入得:a2+b2=74,
则原式=a2+b2﹣2ab=74+10=84,
故答案为:84
11.解:由题可知,25张卡片总面积为4a2+12ab+9b2,
∵4a2+6ab+9b2=(2a+3b)2,
∴这个正方形边长为2a+3b.
故答案为:2a+3b.
12.解:∵a+b=3,ab=﹣1,
∴a2+ab+b2
=(a+b)2﹣ab
=32﹣(﹣1)
=10,
故答案为:10.
13.解:∵a+10=b+12=c+15
∴a+10=b+12 a﹣b=2
同理得a﹣c=5,b﹣c=3
a2+b2+c2﹣ab﹣bc﹣ac=[(a2﹣2ab+b2)+(b2﹣2bc+c2)+(a2﹣2ac+c2)]=[(a﹣b)2+(b﹣c)2+(a﹣c)2]=(4+25+9)=19
故答案为19
14.解:当a+b=8、ab=12时,
原式=
=
=
=
=8,
故答案为:8.
三.解答题
15.解:(1)x2+y2=(x+y)2﹣2xy=72﹣2×(﹣8)=65.
(2)(x﹣y)2=(x+y)2﹣4xy=72﹣4×(﹣8)=81
16.解:(1)∵(a+b)2=5,(a﹣b)2=3,
∴a2+2ab+b2=5,a2﹣2ab+b2=3,
∴2(a2+b2)=8,
解得:a2+b2=4;
(2)∵a2+b2=4,
∴4+2ab=5,
解得:ab=,
∴6ab=3.
17.解:(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)①∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2
=(a+b+c)2﹣(2ab+2ac+2bc)
=112﹣2×38
=45;
②∵2x×4y÷8z=,
∴2x×22y÷23z=,
∴2x+2y﹣3z=2﹣2,
∴x+2y﹣3z=﹣2,
∵(x+2y﹣3z)2=x2+4y2+9z2+2(2xy﹣3xz﹣6yz),x2+4y2+9z2=44,
∴(﹣2)2=44+2(2xy﹣3xz﹣6yz),
∴2xy﹣3xz﹣6yz=﹣20.
18.解:(1)图②中的阴影部分的小正方形的边长=m﹣n;
(2)方法①(m+n)2﹣4mn;
方法②(m﹣n)2;
(3)这三个代数式之间的等量关系是:
(m+n)2=(m﹣n)2+4mn;
(4)(a﹣b)2=(a+b)2﹣4ab,
∵a+b=6,ab=5,
∴(a﹣b)2=36﹣20=16,
∴a﹣b=±4.
故答案为m﹣n;(m+n)2﹣4mn (m﹣n)2;(m+n)2=(m﹣n)2+4mn.
19.解:(1)由图可得,S1=a2﹣b2,
S2=a2﹣a(a﹣b)﹣b(a﹣b)﹣b(a﹣b)=2b2﹣ab;
(2)S1+S2=a2﹣b2+2b2﹣ab=a2+b2﹣ab,
∵a+b=10,ab=20,
∴S1+S2=a2+b2﹣ab=(a+b)2﹣3ab=100﹣3×20=40;
(3)由图可得,S3=a2+b2﹣b(a+b)﹣a2=(a2+b2﹣ab),
∵S1+S2=a2+b2﹣ab=30,
∴S3=×30=15.
20.解:(1)由题意得:图2中阴影部分的正方形边长为:a﹣b.
故答案为:a﹣b.
(2)图2中阴影部分面积为:(a﹣b)2,还可以表示为:(a+b)2﹣4ab.
∴(a﹣b)2=(a+b)2﹣4ab.
(3)设AC=x,BC=y,由题意得:x+y=8,x2+y2=S1+S2=34.
∵(x+y)2=x2+y2+2xy.
∴64=34+2xy.
∴xy=15.
∴S阴影=AC CF=xy=7.5.
一.选择题
1.下列计算正确的是( )
A.(2a+b)2=4a2+b2
B.(5x﹣2y)2=25x2﹣10xy+4y2
C.(x﹣y)2=x2﹣xy+y2
D.(x+)2=x2+x+
2.已知(x﹣2020)2+(x﹣2022)2=18,则(x﹣2021)2的值是( )
A.4 B.8 C.12 D.16
3.若x2+2mx+16是完全平方式,则(m﹣1)2+2的值是( )
A.11 B.3 C.11或27 D.3或11
4.若9x2﹣(K﹣1)x+1是关于x的完全平方式,则常数K的值为( )
A.0 B.﹣5或7 C.7 D.9
5.如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为56,面积之和为58,则长方形ABCD的面积为( )
A.98 B.49 C.20 D.10
6.将四个长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=2S2,则a,b满足( )
A.a=2b B.a=3b C.2a=3b D.2a=5b
二.填空题
7.若a﹣b=5,ab=3,则a2+b2= .
8.多项式x2+2mx+64是完全平方式,则m= .
9.已知x+=3,那么= .
10.若a+b=8,ab=﹣5,则(a﹣b)2= .
11.如图,有三种卡片,其中边长为a的正方形卡片4张,边长分别为a、b的矩形卡片12张,边长为b的正方形卡片9张.用这25张卡片拼成一个正方形,则这个正方形的边长为 .
12.已知a+b=3,ab=﹣1,则a2+ab+b2= .
13.已知a+10=b+12=c+15,则a2+b2+c2﹣ab﹣bc﹣ac= .
14.已知a+b=8,ab=12,则﹣ab= .
三.解答题
15.已知x+y=7,xy=﹣8,求
(1)x2+y2的值; (2)(x﹣y)2的值.
16.已知(a+b)2=5,(a﹣b)2=3,求下列式子的值:
(1)a2+b2; (2)6ab.
17.如图,将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形.
(1)若用不同的方法计算这个边长为(a+b+c)的正方形面积,就可以得到一个等式,这个等式可以为 (只要写出一个即可);
(2)请利用(1)中的等式解答下列问题:
①若三个实数a,b,c满足a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
②若三个实数x,y,z满足2x×4y÷8z=,x2+4y2+9z2=44,求2xy﹣3xz﹣6yz的值.
18.如图①所示是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)图②中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法表示图②中阴影部分的面积.
方法① ;方法② .
(3)观察图②,请写出(m+n)2、(m﹣n)2、mn这三个代数式之间的等量关系: .
(4)若a+b=6,ab=5,则求a﹣b的值.
19.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a,b的代数式分别表示S1、S2;
(2)若a+b=10,ab=20,求S1+S2的值;
(3)当S1+S2=30时,求出图3中阴影部分的面积S3.
20.如图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=34,求图中阴影部分面积.
参考答案
一.选择题
1.解:A、(2a+b)2=4a2+4ab+b2,原计算错误,故此选项不符合题意;
B、(5x﹣2y)2=25x2﹣20xy+4y2,原计算错误,故此选项不符合题意;
C、(x﹣y)2=x2﹣xy+y2,原计算错误,故此选项不符合题意误;
D、原计算正确,故此选项符合题意.
故选:D.
2.解:∵(x﹣2020)2+(x﹣2022)2=18,
∴[(x﹣2021)+1]2+[(x﹣2021)﹣1]2=18,
∴(x﹣2021)2+2(x﹣2021)+1+(x﹣2021)2﹣2(x﹣2021)+1=18,
∴(x﹣2021)2=8.
故选:B.
3.解:∵x2+2mx+16是完全平方式.
∴m2=16.
∴m=±4.
当m=4时,(m﹣1)2+2=9+2=11.
当m=﹣4时(m﹣1)2+2=25+2=27.
故答案为:C.
故选:C.
4.解:9x2﹣(K﹣1)x+1=(3x)2﹣(K﹣1)x+12.
∵9x2﹣(K﹣1)x+1是关于x的完全平方式,
∴9x2﹣(K﹣1)x+1=(3x)2±2 3x 1+12=(3x)2±6x+12.
∴﹣(K﹣1)=±6.
当﹣(K﹣1)=6时,K=﹣5.
当﹣(K﹣1)=﹣6时,K=7.
综上:K=﹣5或7.
故选:B.
5.解:设AB=DC=x,AD=BC=y,由题意得:
化简得:
将①两边平方再减去②得:2xy=20
∴xy=10
故选:D.
6.解:∵S1=2×b(a+b)+2×ab+2×(a﹣b)
=a2+2b2,
S2=(a+b)2﹣(a2+2b2)
=2ab﹣b2,
又∵S1=2S2,
∴a2+2b2=2(2ab﹣b2),
整理,得(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:A.
二.填空题
7.解:把a﹣b=5两边平方得:(a﹣b)2=a2+b2﹣2ab=25,
将ab=3代入得:a2+b2=31,
故答案为:31
8.解:∵x2+2mx+64是完全平方式,
∴2mx=±2 x 8,
∴m=±8.
9.解:∵x+=3,
∴x2+=(x+)2﹣2=7,
∴=(x2+)2﹣2=47.
10.解:把a+b=8两边平方得:(a+b)2=a2+b2+2ab=64,
将ab=﹣5代入得:a2+b2=74,
则原式=a2+b2﹣2ab=74+10=84,
故答案为:84
11.解:由题可知,25张卡片总面积为4a2+12ab+9b2,
∵4a2+6ab+9b2=(2a+3b)2,
∴这个正方形边长为2a+3b.
故答案为:2a+3b.
12.解:∵a+b=3,ab=﹣1,
∴a2+ab+b2
=(a+b)2﹣ab
=32﹣(﹣1)
=10,
故答案为:10.
13.解:∵a+10=b+12=c+15
∴a+10=b+12 a﹣b=2
同理得a﹣c=5,b﹣c=3
a2+b2+c2﹣ab﹣bc﹣ac=[(a2﹣2ab+b2)+(b2﹣2bc+c2)+(a2﹣2ac+c2)]=[(a﹣b)2+(b﹣c)2+(a﹣c)2]=(4+25+9)=19
故答案为19
14.解:当a+b=8、ab=12时,
原式=
=
=
=
=8,
故答案为:8.
三.解答题
15.解:(1)x2+y2=(x+y)2﹣2xy=72﹣2×(﹣8)=65.
(2)(x﹣y)2=(x+y)2﹣4xy=72﹣4×(﹣8)=81
16.解:(1)∵(a+b)2=5,(a﹣b)2=3,
∴a2+2ab+b2=5,a2﹣2ab+b2=3,
∴2(a2+b2)=8,
解得:a2+b2=4;
(2)∵a2+b2=4,
∴4+2ab=5,
解得:ab=,
∴6ab=3.
17.解:(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)①∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2
=(a+b+c)2﹣(2ab+2ac+2bc)
=112﹣2×38
=45;
②∵2x×4y÷8z=,
∴2x×22y÷23z=,
∴2x+2y﹣3z=2﹣2,
∴x+2y﹣3z=﹣2,
∵(x+2y﹣3z)2=x2+4y2+9z2+2(2xy﹣3xz﹣6yz),x2+4y2+9z2=44,
∴(﹣2)2=44+2(2xy﹣3xz﹣6yz),
∴2xy﹣3xz﹣6yz=﹣20.
18.解:(1)图②中的阴影部分的小正方形的边长=m﹣n;
(2)方法①(m+n)2﹣4mn;
方法②(m﹣n)2;
(3)这三个代数式之间的等量关系是:
(m+n)2=(m﹣n)2+4mn;
(4)(a﹣b)2=(a+b)2﹣4ab,
∵a+b=6,ab=5,
∴(a﹣b)2=36﹣20=16,
∴a﹣b=±4.
故答案为m﹣n;(m+n)2﹣4mn (m﹣n)2;(m+n)2=(m﹣n)2+4mn.
19.解:(1)由图可得,S1=a2﹣b2,
S2=a2﹣a(a﹣b)﹣b(a﹣b)﹣b(a﹣b)=2b2﹣ab;
(2)S1+S2=a2﹣b2+2b2﹣ab=a2+b2﹣ab,
∵a+b=10,ab=20,
∴S1+S2=a2+b2﹣ab=(a+b)2﹣3ab=100﹣3×20=40;
(3)由图可得,S3=a2+b2﹣b(a+b)﹣a2=(a2+b2﹣ab),
∵S1+S2=a2+b2﹣ab=30,
∴S3=×30=15.
20.解:(1)由题意得:图2中阴影部分的正方形边长为:a﹣b.
故答案为:a﹣b.
(2)图2中阴影部分面积为:(a﹣b)2,还可以表示为:(a+b)2﹣4ab.
∴(a﹣b)2=(a+b)2﹣4ab.
(3)设AC=x,BC=y,由题意得:x+y=8,x2+y2=S1+S2=34.
∵(x+y)2=x2+y2+2xy.
∴64=34+2xy.
∴xy=15.
∴S阴影=AC CF=xy=7.5.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
