9.1.1不等式及其解集 课件(共41张PPT)
文档属性
| 名称 | 9.1.1不等式及其解集 课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 16:49:08 | ||
图片预览









文档简介
(共41张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第九章 不等式与不等式组
9.1.1 不等式及其解集
1.了解不等式及其解的概念.
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
3.理解不等式的解集及解不等式的意义.
学习目标
如图所示,小明与小丽比身高,小丽身高为
q cm,小明身高为p cm,小丽站在20 cm高的箱子上还没有小明高,则q+20与p哪个大
想一想
情境导入
新知一 不等式的概念
如图所示,处于平衡状态的托盘天平的右盘放上一质量为 50 g 的砝码,左盘放上一个圆球后向左倾斜,问圆球的质量 x g 与质量为 50 g 的砝码之间具有怎样的关系?
x g
50 g
合作探究
我们很容易知道圆球的质量大于砝码的质量,即 x > 50.
某商场推出了购物领红包活动.顾客购物满 100 元即可获得 1 个现金红包,红包金额随机,高于 1 元,且低于 100 元.你能用关系式表示可获红包金额 x 的大小吗?
x>1 且 x<100
问题 一辆匀速行驶的汽车在 11 : 20 距离 A 地 50 千米,要在 12 : 00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从时间上看,汽车要在 12 : 00 之前驶过 A 地,
则以这个速度行驶 50 km 所用的时间不到 h,即
. ①
问题 一辆匀速行驶的汽车在 11 :20 距离 A 地 50 千米,要在 12 :00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从路程上看,汽车要在 12 : 00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即
. ②
式子①和②从不同角度表示了车速应满足的条件.
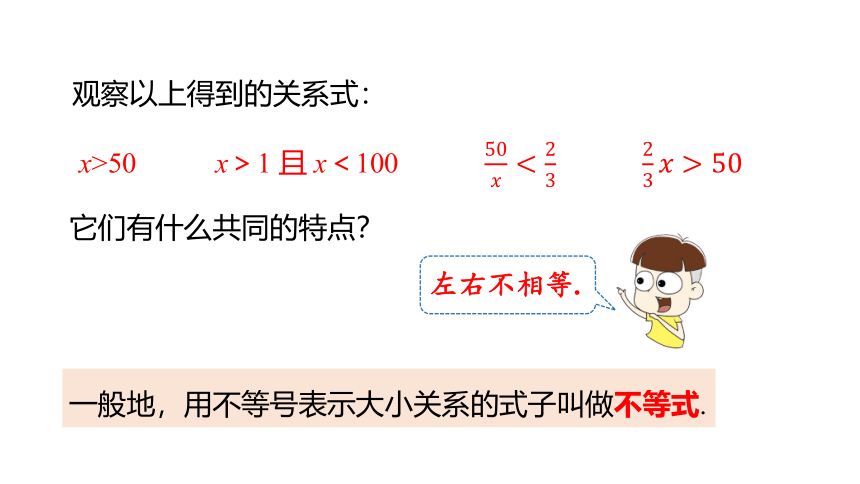
观察以上得到的关系式:
x>50 x>1 且 x<100
左右不相等.
它们有什么共同的特点?
一般地,用不等号表示大小关系的式子叫做不等式.
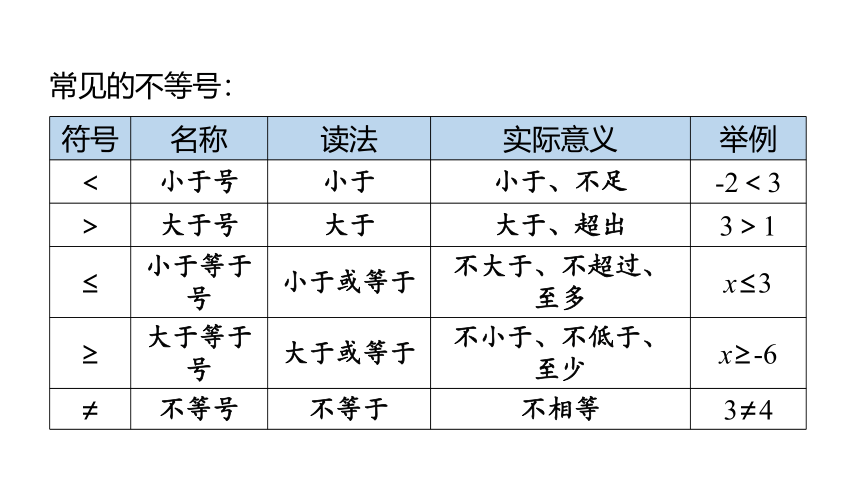
常见的不等号:
符号 名称 读法 实际意义 举例
< 小于号 小于 小于、不足 -2<3
> 大于号 大于 大于、超出 3>1
≤ 小于等于号 小于或等于 不大于、不超过、至多 x≤3
≥ 大于等于号 大于或等于 不小于、不低于、至少 x≥-6
≠ 不等号 不等于 不相等 3≠4
有些不等式中不含未知数,如 3<4;有些不等式中含有未知数,如 2x<1.对于含有未知数的不等式,当未知数取某些值时,不等式的左、右两边符合不等号所表示的大小关系,我们就说不等式成立;否则,不等式不成立.
不等号具有方向性,不等号两边的数不能随意交换.
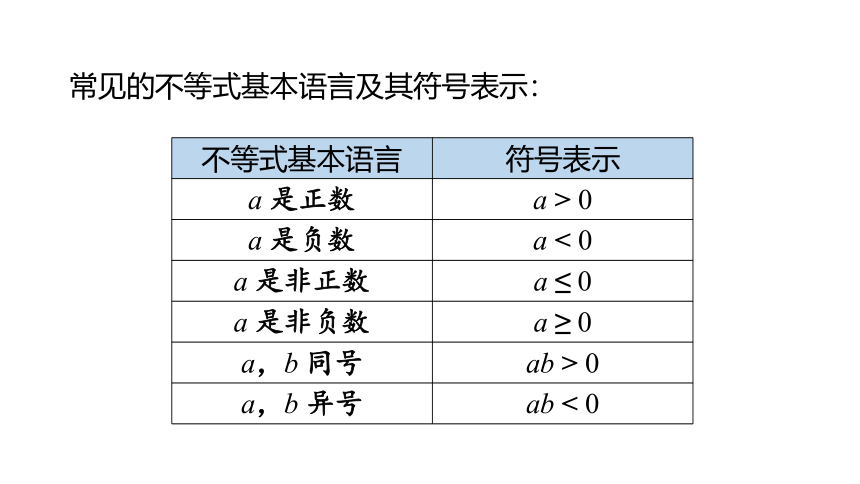
常见的不等式基本语言及其符号表示:
不等式基本语言 符号表示
a 是正数 a > 0
a 是负数 a < 0
a 是非正数 a ≤ 0
a 是非负数 a ≥ 0
a,b 同号 ab > 0
a,b 异号 ab < 0
下列式子中是不等式的有_________.(填序号)
① 3<2;
② 2x2-3>0;
③ 5y2-8;
④ 2x+3=7;
⑤ 3x+1≤7;
⑥ x≠5.
不含不等号
含等号
①②⑤⑥
巩固新知
新知二 不等式的解与解集
下面给出的数,能使不等式 x>50 成立吗?
20, 50, 100.
当x=20时,20<50,不成立.
当x=50时,50=50,不成立.
当x=100时,100>50, 成立.
合作探究
使不等式成立的未知数的值叫做不等式的解.
一般情况下,不等式的解有无数个,但不等式的特殊解可以是有限个.
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
求不等式的解集的过程叫做解不等式.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别
联系 解集包含所有的解,所有的解组成解集
能使不等式成立的未知数的值
能使不等式成立的所有未知数的值
怎样表示不等式的解集呢?
用式子:
用最简形式的不等式(如 x>a 或 x用数轴:
一般标出数轴上某一区间,其中的点对应的数值都是不等式的解.
不等式的解集 x > a x < a x ≥ a x ≤ a
数轴表示
用数轴表示不等式的解集的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点).
2.定方向:大于向右,小于向左.
0
a
0
a
0
a
0
a
常见不等式的解集在数轴上的表示:
1.在 -2,-2.5,0,1 中,是不等式 2x>1 的解的是______.
2×(-2)=-4<1
2×0=0<1
2×(-2.5)=-5<1
1
2.下列说法中,正确的是( )
A. -3 是不等式 x+4<1 的解
B. x>1 是不等式 x+1>0 的解集
C. 不等式 x≥-3 的负整数解有无数个
D. 不等式 x<5 的非正整数解有无数个
-3+4=1
0+1>0,但0<1
-3,-2,-1
D
巩固新知
用不等号表示大小关系的式子
不等式
概念
使不等式成立的未知数的值
解
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集
解集
归纳新知
1.下列式子:①a+b=b+a;②-3>-5;③x≠1;④x+3>6;⑤2m<n;⑥2x-3,其中不等式有( )
A.2个 B.3个 C.4个 D.5个
2.某市最高气温是33℃,最低气温是24℃,则该市气温t(℃)的变化范围是( )
A.t>33 B.t≤24
C.24<t<33 D.24≤t≤33
C
D
课堂练习
C
4.无论x取什么数,下列不等式总成立的是( )
A.x+5>0 B.x+5<0
C.x2<0 D.x2≥0
5.小林在水果摊上称2斤苹果,摊主称了几个苹果说:“你看秤,高高的.”如果设苹果的实际质量为x斤,用不等式把这个“高高的”的意思表示出来是( )
A.x≥2 B.x≤2
C.x>2 D.x<2
D
C
6.(2020·大庆)下列说法中,正确的是( )
A.若a≠b,则a2≠b2
B.若a>|b|,则a>b
C.若|a|=|b|,则a=b
D.若|a|>|b|,则a>b
B
7.用不等式表示:
(1)x与3的差不等于0;
解:x-3≠0.
(2)x的5倍与7的和比x的9倍大;
解:5x+7>9x.
8.下列说法中,错误的是( )
A.不等式x<2的正整数解有一个
B.-2是不等式2x-1<0的一个解
C.不等式-3x>9的解集是x>-3
D.不等式x<10的整数解有无数个
C
9.数4,5,6都是下列不等式解的是( )
A.2x+1>10 B.2x+1≥9
C.x+5≤10 D.3-x>-2
B
10.(2020·吉林)不等式x+1≥2的解集在数轴上表示正确的是( )
A
11.直接写出下列不等式的解集:
(1)x+2>6; (2)3x≤-9;
(3)3x-1>4; (4)x-2>3.
解:x>4.
解:x≤-3.
解:x>5.
12.(2020·贵阳)关于x的不等式的解集在数轴上表示如图所示,则该不等式的解集为______________.
x≤2
13.(2020·临泽县校级期末)已知两个不等式的解集在数轴上如图表示,那么这个解集为( )
A.x≥-1 B.x>1
C.-3<x≤-1 D.x>-3
A
14.如图是某机器零件的设计图纸,用不等式表示零件长度的合格尺寸,则长度L的取值范围是___________________.
39.8≤L≤40.2
15.有如图所示的两种广告牌,其中图①是由两个等腰直角三角形构成的,图②是一个长方形,从图形上确定这两个广告牌面积的大小关系,并将这种大小关系用含字母a,b的不等式表示为____________________.
16.(2020·夏津县期中)请写出满足下列条件的一个不等式.
(1)0是这个不等式的一个解:____________;
(2)-2,-1,0,1都是不等式的解:___________;
(3)0不是这个不等式的解:____________;
(4)与x≤-1的解集相同的不等式:_______________.
x<1
x<2
x<0
x+2≤1
17.将下列不等式的解集在数轴上表示出来:
(1)x<-3; (2)x≥-1;
解: 解:
(3)x≠2; (4)x>-2.
解: 解:
18.已知点P(x,y)位于第二象限,且y<x+4,x,y为整数,写出符合上述条件的点P的坐标.
解:(-1,2),(-1,1),(-2,1).
19.某次数学竞赛中,试题都是选择题,答对一题得5分,不答或答错不得分也不扣分,小颖在本次竞赛中要想得分高于80分,请问她至少应答对多少道题?
解:设她答对了x道题,则有5x>80,x>16,故她至少应答对17道题.
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第九章 不等式与不等式组
9.1.1 不等式及其解集
1.了解不等式及其解的概念.
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
3.理解不等式的解集及解不等式的意义.
学习目标
如图所示,小明与小丽比身高,小丽身高为
q cm,小明身高为p cm,小丽站在20 cm高的箱子上还没有小明高,则q+20与p哪个大
想一想
情境导入
新知一 不等式的概念
如图所示,处于平衡状态的托盘天平的右盘放上一质量为 50 g 的砝码,左盘放上一个圆球后向左倾斜,问圆球的质量 x g 与质量为 50 g 的砝码之间具有怎样的关系?
x g
50 g
合作探究
我们很容易知道圆球的质量大于砝码的质量,即 x > 50.
某商场推出了购物领红包活动.顾客购物满 100 元即可获得 1 个现金红包,红包金额随机,高于 1 元,且低于 100 元.你能用关系式表示可获红包金额 x 的大小吗?
x>1 且 x<100
问题 一辆匀速行驶的汽车在 11 : 20 距离 A 地 50 千米,要在 12 : 00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从时间上看,汽车要在 12 : 00 之前驶过 A 地,
则以这个速度行驶 50 km 所用的时间不到 h,即
. ①
问题 一辆匀速行驶的汽车在 11 :20 距离 A 地 50 千米,要在 12 :00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从路程上看,汽车要在 12 : 00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即
. ②
式子①和②从不同角度表示了车速应满足的条件.
观察以上得到的关系式:
x>50 x>1 且 x<100
左右不相等.
它们有什么共同的特点?
一般地,用不等号表示大小关系的式子叫做不等式.
常见的不等号:
符号 名称 读法 实际意义 举例
< 小于号 小于 小于、不足 -2<3
> 大于号 大于 大于、超出 3>1
≤ 小于等于号 小于或等于 不大于、不超过、至多 x≤3
≥ 大于等于号 大于或等于 不小于、不低于、至少 x≥-6
≠ 不等号 不等于 不相等 3≠4
有些不等式中不含未知数,如 3<4;有些不等式中含有未知数,如 2x<1.对于含有未知数的不等式,当未知数取某些值时,不等式的左、右两边符合不等号所表示的大小关系,我们就说不等式成立;否则,不等式不成立.
不等号具有方向性,不等号两边的数不能随意交换.
常见的不等式基本语言及其符号表示:
不等式基本语言 符号表示
a 是正数 a > 0
a 是负数 a < 0
a 是非正数 a ≤ 0
a 是非负数 a ≥ 0
a,b 同号 ab > 0
a,b 异号 ab < 0
下列式子中是不等式的有_________.(填序号)
① 3<2;
② 2x2-3>0;
③ 5y2-8;
④ 2x+3=7;
⑤ 3x+1≤7;
⑥ x≠5.
不含不等号
含等号
①②⑤⑥
巩固新知
新知二 不等式的解与解集
下面给出的数,能使不等式 x>50 成立吗?
20, 50, 100.
当x=20时,20<50,不成立.
当x=50时,50=50,不成立.
当x=100时,100>50, 成立.
合作探究
使不等式成立的未知数的值叫做不等式的解.
一般情况下,不等式的解有无数个,但不等式的特殊解可以是有限个.
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
求不等式的解集的过程叫做解不等式.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别
联系 解集包含所有的解,所有的解组成解集
能使不等式成立的未知数的值
能使不等式成立的所有未知数的值
怎样表示不等式的解集呢?
用式子:
用最简形式的不等式(如 x>a 或 x
一般标出数轴上某一区间,其中的点对应的数值都是不等式的解.
不等式的解集 x > a x < a x ≥ a x ≤ a
数轴表示
用数轴表示不等式的解集的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点).
2.定方向:大于向右,小于向左.
0
a
0
a
0
a
0
a
常见不等式的解集在数轴上的表示:
1.在 -2,-2.5,0,1 中,是不等式 2x>1 的解的是______.
2×(-2)=-4<1
2×0=0<1
2×(-2.5)=-5<1
1
2.下列说法中,正确的是( )
A. -3 是不等式 x+4<1 的解
B. x>1 是不等式 x+1>0 的解集
C. 不等式 x≥-3 的负整数解有无数个
D. 不等式 x<5 的非正整数解有无数个
-3+4=1
0+1>0,但0<1
-3,-2,-1
D
巩固新知
用不等号表示大小关系的式子
不等式
概念
使不等式成立的未知数的值
解
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集
解集
归纳新知
1.下列式子:①a+b=b+a;②-3>-5;③x≠1;④x+3>6;⑤2m<n;⑥2x-3,其中不等式有( )
A.2个 B.3个 C.4个 D.5个
2.某市最高气温是33℃,最低气温是24℃,则该市气温t(℃)的变化范围是( )
A.t>33 B.t≤24
C.24<t<33 D.24≤t≤33
C
D
课堂练习
C
4.无论x取什么数,下列不等式总成立的是( )
A.x+5>0 B.x+5<0
C.x2<0 D.x2≥0
5.小林在水果摊上称2斤苹果,摊主称了几个苹果说:“你看秤,高高的.”如果设苹果的实际质量为x斤,用不等式把这个“高高的”的意思表示出来是( )
A.x≥2 B.x≤2
C.x>2 D.x<2
D
C
6.(2020·大庆)下列说法中,正确的是( )
A.若a≠b,则a2≠b2
B.若a>|b|,则a>b
C.若|a|=|b|,则a=b
D.若|a|>|b|,则a>b
B
7.用不等式表示:
(1)x与3的差不等于0;
解:x-3≠0.
(2)x的5倍与7的和比x的9倍大;
解:5x+7>9x.
8.下列说法中,错误的是( )
A.不等式x<2的正整数解有一个
B.-2是不等式2x-1<0的一个解
C.不等式-3x>9的解集是x>-3
D.不等式x<10的整数解有无数个
C
9.数4,5,6都是下列不等式解的是( )
A.2x+1>10 B.2x+1≥9
C.x+5≤10 D.3-x>-2
B
10.(2020·吉林)不等式x+1≥2的解集在数轴上表示正确的是( )
A
11.直接写出下列不等式的解集:
(1)x+2>6; (2)3x≤-9;
(3)3x-1>4; (4)x-2>3.
解:x>4.
解:x≤-3.
解:x>5.
12.(2020·贵阳)关于x的不等式的解集在数轴上表示如图所示,则该不等式的解集为______________.
x≤2
13.(2020·临泽县校级期末)已知两个不等式的解集在数轴上如图表示,那么这个解集为( )
A.x≥-1 B.x>1
C.-3<x≤-1 D.x>-3
A
14.如图是某机器零件的设计图纸,用不等式表示零件长度的合格尺寸,则长度L的取值范围是___________________.
39.8≤L≤40.2
15.有如图所示的两种广告牌,其中图①是由两个等腰直角三角形构成的,图②是一个长方形,从图形上确定这两个广告牌面积的大小关系,并将这种大小关系用含字母a,b的不等式表示为____________________.
16.(2020·夏津县期中)请写出满足下列条件的一个不等式.
(1)0是这个不等式的一个解:____________;
(2)-2,-1,0,1都是不等式的解:___________;
(3)0不是这个不等式的解:____________;
(4)与x≤-1的解集相同的不等式:_______________.
x<1
x<2
x<0
x+2≤1
17.将下列不等式的解集在数轴上表示出来:
(1)x<-3; (2)x≥-1;
解: 解:
(3)x≠2; (4)x>-2.
解: 解:
18.已知点P(x,y)位于第二象限,且y<x+4,x,y为整数,写出符合上述条件的点P的坐标.
解:(-1,2),(-1,1),(-2,1).
19.某次数学竞赛中,试题都是选择题,答对一题得5分,不答或答错不得分也不扣分,小颖在本次竞赛中要想得分高于80分,请问她至少应答对多少道题?
解:设她答对了x道题,则有5x>80,x>16,故她至少应答对17道题.
https://www.21cnjy.com/help/help_extract.php
