9.1.2不等式的性质(第1课时) 课件(共36张PPT)
文档属性
| 名称 | 9.1.2不等式的性质(第1课时) 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 16:46:16 | ||
图片预览









文档简介
(共36张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第九章 不等式与不等式组
9.1.2 不等式的性质
第1课时
1.理解并掌握不等式的基本性质。
2.体会探索过程中所应用的归纳和类比方法。
学习目标
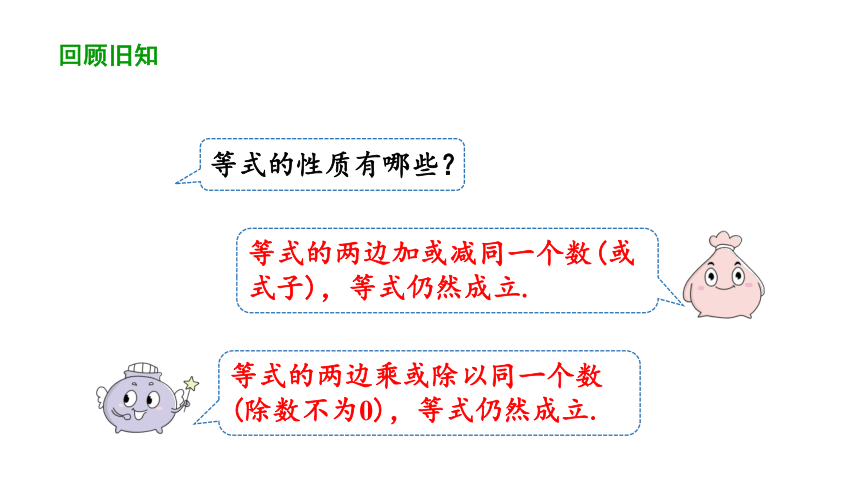
设“▲”“●”“■”分别表示三种不同的物体,现用天平称两次,情况如图所示,把▲,●,■这三种物体按质量从大到小排列.
想一想
解:设▲,●,■的质量分别为a,b,c,根据图形,可得a+c>2a,2a=3b,故可得c>a>b.即■>▲>●.
情境导入
等式的性质有哪些?
等式的两边加或减同一个数(或式子),等式仍然成立.
等式的两边乘或除以同一个数(除数不为0),等式仍然成立.
回顾旧知
比你大两岁,所以我是你哥哥.
哈哈!三年前我还是比你大.
呵呵,再过二十年,你也比我小!
大两岁,那三年前,你不就比我小呀!
哦?那…再过十年,我肯定比你大.
导入新知
新知 不等式的性质
思考1 用“<”或“>”填空,并总结其中的规律:
① 5>3
5+2 3+2, 5+(-2) 3+(-2), 5+0 3+0 ;
② -1<3
-1+2 3+2,-1+(-3) 3+(-3), -1+0 3+0.
>
>
>
<
<
<
规律:当不等式两边加或减同一个数(正数或负数)时,不等号的方向不变.
合作探究
你能总结出不等式的性质吗?
符号语言:如果 a>b,那么 a±c>b±c.
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
思考2 用“<”或“>”填空,并总结其中的规律:
① 6>2
6×4 2×4, 6÷2 2÷2;
② -2<4
-2×2 4×2,-2÷2 4÷2;
③ -4<-2
-4×2 -2×2,-4÷2 -2÷2.
>
>
<
<
<
<
规律:当不等式两边乘(或除以)同一个正数时,不等号的方向不变.
符号语言:如果 a>b,c>0,那么 ac>bc(或).
你能总结出不等式的性质吗?
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
两边同乘的数不能是 0,若两边同乘 0,则不等式变为等式 0=0;两边同时除以的数也不能是 0,因为 0 作为除数无意义.
思考3 用“<”或“>”填空,并总结其中的规律:
① 6>2
6×(-4) 2×(-4), 6÷(-2) 2÷(-2);
② -2<4
-2×(-2) 4×(-2),-2÷(-2) 4÷(-2);
③ -4<-2
-4×(-2) -2×(-2),-4÷(-2) -2÷(-2).
<
<
>
>
>
>
规律:当不等式两边乘(或除以)同一个负数时,不等
号的方向改变.
符号语言:如果 a>b,c<0,那么 ac你能总结出不等式的性质吗?
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
运用不等式的性质对不等式进行变形时,要特别注意性质 2 和性质 3 的区别,在乘(或除以)同一个数时,必须先弄清这个数是正数还是负数,如果是负数,不等号的方向要改变.
不等式的其他性质:
(1)对称性( 反身性):若 a>b,则 b(2)传递性:若 a>b,b>c,则 a>c.
不等式的性质与等式的性质的不同点和相同点
类别 不同点 相同点
不等式 两边乘(或除以)同一个负数,不等号的方向要改变. (1)两边加(或减)同一个数(或式子),不等式和等式仍成立;
(2)两边乘(或除以)同一个正数,不等式和等式仍成立.
等式 两边乘(或除以)同一个负数,等式仍然成立.
设 a>b,用“<”或“>”填空.
(1) a+2____b+2;
(2) a-3____b-3;
(3) -4a____-4b;
(4) ____ .
>
>
<
>
加同一个数,不等号方向不变
减同一个数,不等号方向不变
乘同一个负数,不等号方向改变
除以同一个正数,不等号方向不变
巩固新知
1.若 m>n,则下列不等式不一定成立的是( )
A. m+3>n+3
B. -3m<-3n
C.
D. m2>n2
加同一个数,不等号方向不变
除以同一个正数,不等号方向不变
乘同一个负数,不等号方向改变
当 m=2,n=-3 时,m2D
课堂练习
2.如果 a>b,c<0,那么下列不等式成立的是( )
A. a+c>b
B. a+c>b-c
C.ac-1>bc-1
D.a(c-1)c-1<0
乘同一个负数,不等号方向改变
D
3.用适当的不等号填空:
(1)若 a-1(2)若 -3a<-3b,则 a____b;
(3)若 0.3a+1<0.3b+1,则 a___b.
<
>
<
两边同时加1
两边同时除以-3
0.3a<0.3b
a两边同时减1
两边同时除以0.3
如果 a>b,c<0,
那么 ac如果 a>b,
那么 a±c>b±c.
如果 a>b,c>0,
那么 ac>bc(或).
不等式的基本性质
性质1
性质2
性质3
归纳新知
1.下列不等式变形正确的是( )
A.由a>b得ac>bc
B.由a>b得-2a>-2b
C.由a>b得-a<-b
D.由a>b得a-2<b-2
C
课后练习
D
D
4.用“<”或“>”填空:
(1)若m>n,则m-1____n-1;
(2)若x<y,则x+a____y+a;
(3)若a+2>b+2,则a____b;
(4)若-3m>-3n,则m____n.
>
<
>
<
A
D
1
5-2
x>3
2
3
8.(柳州中考)不等式x+1≥0的解集是____________.
9.利用不等式的性质解下列不等式:
(1)3x-8>1; (2)x<3x-4;
解:x>3
x≥-1
解:x>2
解:x<-1
解:x<9
10.(常州中考)若3x>-3y,则下列不等式中一定成立的是( )
A.x+y>0 B.x-y>0
C.x+y<0 D.x-y<0
11.(2020·杭州)若a>b,则( )
A.a-1≥b B.b+1≥a
C.a+1>b-1 D.a-1>b+1
A
C
12.已知关于x的不等式x-a<1的解集如图所示,则a的值是( )
A.0 B.1 C.2 D.3
B
13.填空:
(1)2-x<0,则x>____;
(2)若x>-2,则 x+2____0;
(3)若-2a≥-8,则a____4.
14.若关于x的不等式(3-m)x<3-m的解集为x>1,
则m的取值范围是____.
2
>
≤
m>3
15.利用不等式的性质解下列不等式.
(1)2x+5<-1;
解:x<-3
(2)2x≥5x-6.
解:x≤2
16.用不等式表示下列语句并写出解集.
(1)x的2倍小于或等于1;
(2)x与3的差不小于1;
解:x-3≥1,解集为x≥4
18.现有不等式的性质:
①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
②在不等式的两边都乘以同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题:
(1)利用性质①比较2a与a的大小(a≠0);
(2)利用性质②比较2a与a的大小(a≠0).
解:(1)当a>0时,在a>0两边同时加上a,得a+a>a+0,即2a>a;
当a<0时,在a<0两边同时加上a,得a+a<a+0,即2a<a
(2)当a>0时,由2>1,得2·a>1·a,即2a>a;
当a<0时,由2>1,得2·a<1·a,即2a<a
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第九章 不等式与不等式组
9.1.2 不等式的性质
第1课时
1.理解并掌握不等式的基本性质。
2.体会探索过程中所应用的归纳和类比方法。
学习目标
设“▲”“●”“■”分别表示三种不同的物体,现用天平称两次,情况如图所示,把▲,●,■这三种物体按质量从大到小排列.
想一想
解:设▲,●,■的质量分别为a,b,c,根据图形,可得a+c>2a,2a=3b,故可得c>a>b.即■>▲>●.
情境导入
等式的性质有哪些?
等式的两边加或减同一个数(或式子),等式仍然成立.
等式的两边乘或除以同一个数(除数不为0),等式仍然成立.
回顾旧知
比你大两岁,所以我是你哥哥.
哈哈!三年前我还是比你大.
呵呵,再过二十年,你也比我小!
大两岁,那三年前,你不就比我小呀!
哦?那…再过十年,我肯定比你大.
导入新知
新知 不等式的性质
思考1 用“<”或“>”填空,并总结其中的规律:
① 5>3
5+2 3+2, 5+(-2) 3+(-2), 5+0 3+0 ;
② -1<3
-1+2 3+2,-1+(-3) 3+(-3), -1+0 3+0.
>
>
>
<
<
<
规律:当不等式两边加或减同一个数(正数或负数)时,不等号的方向不变.
合作探究
你能总结出不等式的性质吗?
符号语言:如果 a>b,那么 a±c>b±c.
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
思考2 用“<”或“>”填空,并总结其中的规律:
① 6>2
6×4 2×4, 6÷2 2÷2;
② -2<4
-2×2 4×2,-2÷2 4÷2;
③ -4<-2
-4×2 -2×2,-4÷2 -2÷2.
>
>
<
<
<
<
规律:当不等式两边乘(或除以)同一个正数时,不等号的方向不变.
符号语言:如果 a>b,c>0,那么 ac>bc(或).
你能总结出不等式的性质吗?
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
两边同乘的数不能是 0,若两边同乘 0,则不等式变为等式 0=0;两边同时除以的数也不能是 0,因为 0 作为除数无意义.
思考3 用“<”或“>”填空,并总结其中的规律:
① 6>2
6×(-4) 2×(-4), 6÷(-2) 2÷(-2);
② -2<4
-2×(-2) 4×(-2),-2÷(-2) 4÷(-2);
③ -4<-2
-4×(-2) -2×(-2),-4÷(-2) -2÷(-2).
<
<
>
>
>
>
规律:当不等式两边乘(或除以)同一个负数时,不等
号的方向改变.
符号语言:如果 a>b,c<0,那么 ac
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
运用不等式的性质对不等式进行变形时,要特别注意性质 2 和性质 3 的区别,在乘(或除以)同一个数时,必须先弄清这个数是正数还是负数,如果是负数,不等号的方向要改变.
不等式的其他性质:
(1)对称性( 反身性):若 a>b,则 b
不等式的性质与等式的性质的不同点和相同点
类别 不同点 相同点
不等式 两边乘(或除以)同一个负数,不等号的方向要改变. (1)两边加(或减)同一个数(或式子),不等式和等式仍成立;
(2)两边乘(或除以)同一个正数,不等式和等式仍成立.
等式 两边乘(或除以)同一个负数,等式仍然成立.
设 a>b,用“<”或“>”填空.
(1) a+2____b+2;
(2) a-3____b-3;
(3) -4a____-4b;
(4) ____ .
>
>
<
>
加同一个数,不等号方向不变
减同一个数,不等号方向不变
乘同一个负数,不等号方向改变
除以同一个正数,不等号方向不变
巩固新知
1.若 m>n,则下列不等式不一定成立的是( )
A. m+3>n+3
B. -3m<-3n
C.
D. m2>n2
加同一个数,不等号方向不变
除以同一个正数,不等号方向不变
乘同一个负数,不等号方向改变
当 m=2,n=-3 时,m2
课堂练习
2.如果 a>b,c<0,那么下列不等式成立的是( )
A. a+c>b
B. a+c>b-c
C.ac-1>bc-1
D.a(c-1)
乘同一个负数,不等号方向改变
D
3.用适当的不等号填空:
(1)若 a-1
(3)若 0.3a+1<0.3b+1,则 a___b.
<
>
<
两边同时加1
两边同时除以-3
0.3a<0.3b
a
两边同时除以0.3
如果 a>b,c<0,
那么 ac
那么 a±c>b±c.
如果 a>b,c>0,
那么 ac>bc(或).
不等式的基本性质
性质1
性质2
性质3
归纳新知
1.下列不等式变形正确的是( )
A.由a>b得ac>bc
B.由a>b得-2a>-2b
C.由a>b得-a<-b
D.由a>b得a-2<b-2
C
课后练习
D
D
4.用“<”或“>”填空:
(1)若m>n,则m-1____n-1;
(2)若x<y,则x+a____y+a;
(3)若a+2>b+2,则a____b;
(4)若-3m>-3n,则m____n.
>
<
>
<
A
D
1
5-2
x>3
2
3
8.(柳州中考)不等式x+1≥0的解集是____________.
9.利用不等式的性质解下列不等式:
(1)3x-8>1; (2)x<3x-4;
解:x>3
x≥-1
解:x>2
解:x<-1
解:x<9
10.(常州中考)若3x>-3y,则下列不等式中一定成立的是( )
A.x+y>0 B.x-y>0
C.x+y<0 D.x-y<0
11.(2020·杭州)若a>b,则( )
A.a-1≥b B.b+1≥a
C.a+1>b-1 D.a-1>b+1
A
C
12.已知关于x的不等式x-a<1的解集如图所示,则a的值是( )
A.0 B.1 C.2 D.3
B
13.填空:
(1)2-x<0,则x>____;
(2)若x>-2,则 x+2____0;
(3)若-2a≥-8,则a____4.
14.若关于x的不等式(3-m)x<3-m的解集为x>1,
则m的取值范围是____.
2
>
≤
m>3
15.利用不等式的性质解下列不等式.
(1)2x+5<-1;
解:x<-3
(2)2x≥5x-6.
解:x≤2
16.用不等式表示下列语句并写出解集.
(1)x的2倍小于或等于1;
(2)x与3的差不小于1;
解:x-3≥1,解集为x≥4
18.现有不等式的性质:
①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
②在不等式的两边都乘以同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题:
(1)利用性质①比较2a与a的大小(a≠0);
(2)利用性质②比较2a与a的大小(a≠0).
解:(1)当a>0时,在a>0两边同时加上a,得a+a>a+0,即2a>a;
当a<0时,在a<0两边同时加上a,得a+a<a+0,即2a<a
(2)当a>0时,由2>1,得2·a>1·a,即2a>a;
当a<0时,由2>1,得2·a<1·a,即2a<a
https://www.21cnjy.com/help/help_extract.php
