9.1.2不等式的性质(第2课时) 课件(共42张PPT)
文档属性
| 名称 | 9.1.2不等式的性质(第2课时) 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 16:43:39 | ||
图片预览









文档简介
(共42张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第九章 不等式与不等式组
9.1.2 不等式的性质
第2课时
1.进一步了解不等式的基本性质,会用不等式的基本性质解简单的不等式.
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
学习目标
解下列不等式,并把解集表示在数轴上.
(1)x+2<1;
〔解析〕解决本题的关键是掌握不等式的性质,在(1)的两边减2,不等号的方向不变;
解:根据不等式的性质1,在不等式的两边减2,不等号的方向不变,得x+2- 2<1- 2,即x<- 1,这个不等式的解集在数轴上表示如下图所示.
复习巩固
解下列不等式,并把解集表示在数轴上.
(2)2x- 3>0.
〔解析〕 在(2)的两边加3,然后两边除以2,不等号的方向不变.
解:根据不等式的性质1,在不等式的两边加3,得2x- 3+3>3,即2x>3,再根据不等式的性质2,不等式的两边除以2,不等号的方向不变,得x>1.5.这个不等式的解集在数轴上表示如下图所示.
复习巩固
不等式的性质有哪些?
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式两边乘(或除以)同一个负数,不等号的方向改变.
复习巩固
用适当的不等号填空:
(1)若 a+5(2)若 -4a>-4b,则 a____b;
(3)若 ,则 a___b.
<
<
>
两边同时减 5
两边同时除以 -4
a>b
两边同时加 2
两边同时乘 4
我们知道解方程需要依据等式的性质,同样解不等式也可以依据不等式的性质进行,本节课我们就来学习怎样利用不等式的基本性质解不等式.
导入新知
新知 不等式的性质的应用
例1 利用不等式的性质解下列不等式,并在数轴上表示解集.
(1) x-7>26; (2) 3x<2x+1;
(3) >50; (4) -4x>3.
分析:解不等式,就是要借助不等式的性质使不等式逐步化为 x>a 或 x合作探究
解:(1)根据不等式的性质1,不等式两边加 7,不等号的方向不变,
所以 x-7+7>26+7,
即 x>33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26;
0
1
(2) 3x<2x+1;
解:(2)根据不等式的性质1,不等式两边减 2x,不等号的方向不变,
所以 3x-2x<2x+1-2x,
即 x<1.
这个不等式的解集在数轴上的表示如图所示:
0
75
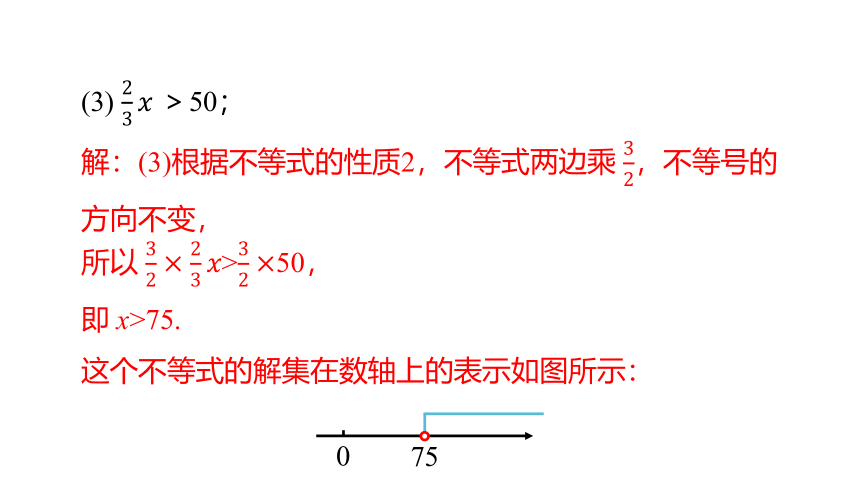
(3) >50;
解:(3)根据不等式的性质2,不等式两边乘 ,不等号的方向不变,
所以 >50,
即 x>75.
这个不等式的解集在数轴上的表示如图所示:
(4) -4x>3.
解:(4)根据不等式的性质3,不等式两边除以 -4,不等号的方向改变,
所以 ,
即 x< .
这个不等式的解集在数轴上的表示如图所示:
0
利用不等式的性质1可简化为“移项”;利用不等式的性质2或性质3就是把未知数的系数化为1,要注意不等式两边乘(或除以)同一个负数时,不等号要改变方向.
例2 某长方体形状的容器长 5 cm,宽 3 cm,高 10 cm,容器内原有水的高度为 3 cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出 V 的取值范围.
5 cm
3 cm
10 cm
解:新注入水的体积 V 与原有水的体积的和不能超过容器的容积,即
V+3×5×3≤3×5×10,
V≤105.
又由于新注入水的体积不能是负数,
因此,V 的取值范围是 V ≥0 并且 V≤105.
在数轴上表示 V 的取值范围如图所示:
在表示 0 和 105 的点上画实心圆点,表示取值范围包含这两个数.
0
105
①审:审清题意,弄懂已知什么,求什么,以及各个数量之间的关系.
②设:设未知数,一般是与所求问题有直接关系的量.
③找:找出题中所有的不等关系,特别是隐含的数量关系.
④列:列出不等式.
⑤解:分别解出每个不等式的解集,再求其公共部分,得出结果.
⑥答:根据所得结果作出回答.
列不等式处理实际问题的一般步骤:
用不等式的性质解下列不等式,并在数轴上表示解集.
(1) x+5>-1;
解:(1)根据不等式的性质1,不等式两边减 5,不等号的方向不变,
所以 x+5-5>-1-5,
即 x>-6.
这个不等式的解集在数轴上的表示如图所示:
0
-6
巩固新知
用不等式的性质解下列不等式,并在数轴上表示解集.
(2) 4x<3x-5;
解:(2)根据不等式的性质1,不等式两边减 3x,不等号的方向不变,
所以 4x-3x<3x-5-3x ,
即 x<-5.
这个不等式的解集在数轴上的表示如图所示:
0
-5
用不等式的性质解下列不等式,并在数轴上表示解集.
(3) ;
解:(3)根据不等式的性质2,不等式两边乘 7,不等号的方向不变,
所以 ,即 x<6.
这个不等式的解集在数轴上的表示如图所示:
0
6
用不等式的性质解下列不等式,并在数轴上表示解集.
(4) -8x>10.
解:(4)根据不等式的性质3,不等式两边除以 -8,不等号的方向改变,
所以 ,即 x< .
这个不等式的解集在数轴上的表示如图所示:
0
列不等式处理实际问题的一般步骤:
审
设
找
列
解
答
归纳新知
B
课堂练习
C
3.(2020·株洲)已知实数a,b满足a+1>b+1,则下列选项可能错误的是( )
A.a>b B.a+2>b+2
C.-a<-b D.2a>3b
D
>
不等式性质1
<
不等式性质2
<
不等式性质1
>
不等式性质3
A
6.(2020·六盘水)不等式3x+6≥9的解集在数轴上表示正确的是( )
C
8.某种品牌的八宝粥,外包装标明:净含量为330±10 g,表明了这罐八宝粥的净含量x的范围是( )
A.320 g<x<340 g B.320 g≤x<340 g
C.320 g<x≤340 g D.320 g≤x≤340 g
D
9.如图,x和5分别是天平上两边的砝码,请你用“>”或“<”填空:x-3__________2.
<
C
12.小明的作业本上有四道利用不等式的性质解不等式的作业题,他的解答如下:①由x+7>8解得x>1;②由x<2x+3解得x<3;③由3x-1>x+7解得x>4;④由-3x>-6解得x<-2.其中正确的有( )
A.1题 B.2题 C.3题 D.4题
B
13.某商场推出了一种购物“金卡”,凭此卡在该商场购物可按商品价格的八折优惠,但办理金卡时每张要收100元购卡费,设按标价累计购物金额为x元,当x>___________时,办理金卡购物更省钱.
500
14.判断“如果a>b,那么5-2a<5-2b.”是否正确,如果不正确,请说明理由;如果正确,说明变形的过程和依据.
解:正确.∵a>b,
∴-2a<-2b(不等式的性质3).
∴-2a+5<-2b+5(不等式的性质1),
即5-2a<5-2b.
1
加(-6x+4)
3
除以-11
>
>
>
(2)请你用一个一般的式子描述上述规律;
(3)若a>b,c>d,则ac>bd一定成立吗?若不成立,请举一例子说明,并指出当满足什么条件时,这一规律成立.
解:(2)若a>b,c>d,则a+c>b+d.
(3)不一定成立.例:a=2,b=-3,c=1,d=-2时,ac=2,bd=6,则ac<bd.
当满足a>b>0,c>d>0时,这一规律成立.
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第九章 不等式与不等式组
9.1.2 不等式的性质
第2课时
1.进一步了解不等式的基本性质,会用不等式的基本性质解简单的不等式.
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
学习目标
解下列不等式,并把解集表示在数轴上.
(1)x+2<1;
〔解析〕解决本题的关键是掌握不等式的性质,在(1)的两边减2,不等号的方向不变;
解:根据不等式的性质1,在不等式的两边减2,不等号的方向不变,得x+2- 2<1- 2,即x<- 1,这个不等式的解集在数轴上表示如下图所示.
复习巩固
解下列不等式,并把解集表示在数轴上.
(2)2x- 3>0.
〔解析〕 在(2)的两边加3,然后两边除以2,不等号的方向不变.
解:根据不等式的性质1,在不等式的两边加3,得2x- 3+3>3,即2x>3,再根据不等式的性质2,不等式的两边除以2,不等号的方向不变,得x>1.5.这个不等式的解集在数轴上表示如下图所示.
复习巩固
不等式的性质有哪些?
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式两边乘(或除以)同一个负数,不等号的方向改变.
复习巩固
用适当的不等号填空:
(1)若 a+5
(3)若 ,则 a___b.
<
<
>
两边同时减 5
两边同时除以 -4
a>b
两边同时加 2
两边同时乘 4
我们知道解方程需要依据等式的性质,同样解不等式也可以依据不等式的性质进行,本节课我们就来学习怎样利用不等式的基本性质解不等式.
导入新知
新知 不等式的性质的应用
例1 利用不等式的性质解下列不等式,并在数轴上表示解集.
(1) x-7>26; (2) 3x<2x+1;
(3) >50; (4) -4x>3.
分析:解不等式,就是要借助不等式的性质使不等式逐步化为 x>a 或 x合作探究
解:(1)根据不等式的性质1,不等式两边加 7,不等号的方向不变,
所以 x-7+7>26+7,
即 x>33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26;
0
1
(2) 3x<2x+1;
解:(2)根据不等式的性质1,不等式两边减 2x,不等号的方向不变,
所以 3x-2x<2x+1-2x,
即 x<1.
这个不等式的解集在数轴上的表示如图所示:
0
75
(3) >50;
解:(3)根据不等式的性质2,不等式两边乘 ,不等号的方向不变,
所以 >50,
即 x>75.
这个不等式的解集在数轴上的表示如图所示:
(4) -4x>3.
解:(4)根据不等式的性质3,不等式两边除以 -4,不等号的方向改变,
所以 ,
即 x< .
这个不等式的解集在数轴上的表示如图所示:
0
利用不等式的性质1可简化为“移项”;利用不等式的性质2或性质3就是把未知数的系数化为1,要注意不等式两边乘(或除以)同一个负数时,不等号要改变方向.
例2 某长方体形状的容器长 5 cm,宽 3 cm,高 10 cm,容器内原有水的高度为 3 cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出 V 的取值范围.
5 cm
3 cm
10 cm
解:新注入水的体积 V 与原有水的体积的和不能超过容器的容积,即
V+3×5×3≤3×5×10,
V≤105.
又由于新注入水的体积不能是负数,
因此,V 的取值范围是 V ≥0 并且 V≤105.
在数轴上表示 V 的取值范围如图所示:
在表示 0 和 105 的点上画实心圆点,表示取值范围包含这两个数.
0
105
①审:审清题意,弄懂已知什么,求什么,以及各个数量之间的关系.
②设:设未知数,一般是与所求问题有直接关系的量.
③找:找出题中所有的不等关系,特别是隐含的数量关系.
④列:列出不等式.
⑤解:分别解出每个不等式的解集,再求其公共部分,得出结果.
⑥答:根据所得结果作出回答.
列不等式处理实际问题的一般步骤:
用不等式的性质解下列不等式,并在数轴上表示解集.
(1) x+5>-1;
解:(1)根据不等式的性质1,不等式两边减 5,不等号的方向不变,
所以 x+5-5>-1-5,
即 x>-6.
这个不等式的解集在数轴上的表示如图所示:
0
-6
巩固新知
用不等式的性质解下列不等式,并在数轴上表示解集.
(2) 4x<3x-5;
解:(2)根据不等式的性质1,不等式两边减 3x,不等号的方向不变,
所以 4x-3x<3x-5-3x ,
即 x<-5.
这个不等式的解集在数轴上的表示如图所示:
0
-5
用不等式的性质解下列不等式,并在数轴上表示解集.
(3) ;
解:(3)根据不等式的性质2,不等式两边乘 7,不等号的方向不变,
所以 ,即 x<6.
这个不等式的解集在数轴上的表示如图所示:
0
6
用不等式的性质解下列不等式,并在数轴上表示解集.
(4) -8x>10.
解:(4)根据不等式的性质3,不等式两边除以 -8,不等号的方向改变,
所以 ,即 x< .
这个不等式的解集在数轴上的表示如图所示:
0
列不等式处理实际问题的一般步骤:
审
设
找
列
解
答
归纳新知
B
课堂练习
C
3.(2020·株洲)已知实数a,b满足a+1>b+1,则下列选项可能错误的是( )
A.a>b B.a+2>b+2
C.-a<-b D.2a>3b
D
>
不等式性质1
<
不等式性质2
<
不等式性质1
>
不等式性质3
A
6.(2020·六盘水)不等式3x+6≥9的解集在数轴上表示正确的是( )
C
8.某种品牌的八宝粥,外包装标明:净含量为330±10 g,表明了这罐八宝粥的净含量x的范围是( )
A.320 g<x<340 g B.320 g≤x<340 g
C.320 g<x≤340 g D.320 g≤x≤340 g
D
9.如图,x和5分别是天平上两边的砝码,请你用“>”或“<”填空:x-3__________2.
<
C
12.小明的作业本上有四道利用不等式的性质解不等式的作业题,他的解答如下:①由x+7>8解得x>1;②由x<2x+3解得x<3;③由3x-1>x+7解得x>4;④由-3x>-6解得x<-2.其中正确的有( )
A.1题 B.2题 C.3题 D.4题
B
13.某商场推出了一种购物“金卡”,凭此卡在该商场购物可按商品价格的八折优惠,但办理金卡时每张要收100元购卡费,设按标价累计购物金额为x元,当x>___________时,办理金卡购物更省钱.
500
14.判断“如果a>b,那么5-2a<5-2b.”是否正确,如果不正确,请说明理由;如果正确,说明变形的过程和依据.
解:正确.∵a>b,
∴-2a<-2b(不等式的性质3).
∴-2a+5<-2b+5(不等式的性质1),
即5-2a<5-2b.
1
加(-6x+4)
3
除以-11
>
>
>
(2)请你用一个一般的式子描述上述规律;
(3)若a>b,c>d,则ac>bd一定成立吗?若不成立,请举一例子说明,并指出当满足什么条件时,这一规律成立.
解:(2)若a>b,c>d,则a+c>b+d.
(3)不一定成立.例:a=2,b=-3,c=1,d=-2时,ac=2,bd=6,则ac<bd.
当满足a>b>0,c>d>0时,这一规律成立.
https://www.21cnjy.com/help/help_extract.php
