9.2 一元一次不等式(第2课时) 课件(共38张PPT)
文档属性
| 名称 | 9.2 一元一次不等式(第2课时) 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 16:32:02 | ||
图片预览











文档简介
(共38张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第九章 不等式与不等式组
9.2 一元一次不等式
第2课时 一元一次不等式的应用
1.掌握用一元一次不等式解决实际问题的步骤.
2.培养将实际问题向数学模型转化的能力.
3.初步认识一元一次不等式的应用价值,发展分析问题、解决问题的能力.
学习目标
小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时或11时前追上小明,速度至少应是多少
想一想
〔解析〕这是一个追赶问题,读懂题意后从路程下手找不等关系.小亮40分钟行进路程要比小明从8时20分到11时行进的路程远或二者相等才可以.这样可以得到不等式,进而解决问题.通过上述分析,你能够通过列不等式解决这个问题吗
情境导入
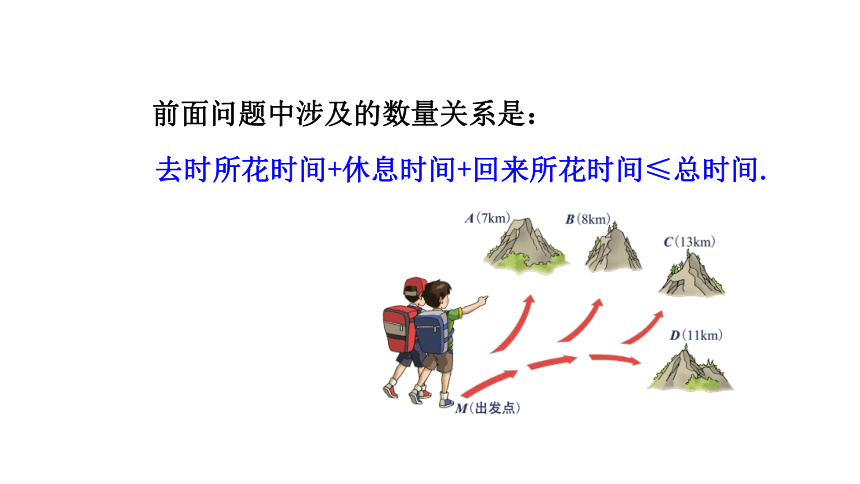
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
新知 一元一次不等式的应用
合作探究
前面问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h,回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 .
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
列不等式解应用题的基本步骤:
(1)审:认真审题,分清已知量、未知量;
(2)找:要抓住题中的关键字找出题中的不等关系;
(3)设:设出适当的未知数;
(4)列:根据题中的不等关系列出不等式;
(5)解:解出所列不等式的解集;
(6)答:检验是否符合题意,写出答案.
归纳小结
例1 去年广州空气质量良好(二级以上)的天数与全年
天数(365天)之比达到60%,如果到明年(365天)这样
的比值要超过70%,那么明年空气质量良好的天数要比
去年至少增加多少?
明年这样的比值要超70%
典例精析1 一元一次不等式的实际应用
分析:题目蕴含的不等关系为 ,
转 化 为 不 等 式,即 .
合作探究
解:设明年比去年空气质量良好的天数增加了 .
去年有 天空气质量良好,明年有 ,
天空气质量良好,并且 > ,
去分母,得 x + > ,
移项,合并同类项,得 x> .
由x应为正整数,得x ≥ .
答:明年要比去年空气质量良好的天数至少增加 ,
才能使这一年空气质量良好的天数超过全年天数的70% .
x天
365×60%
x+365×60%
70%
219
255.5
36.5
37
37天
在一次知识竞赛中,有10道抢答题,答对一题得10分,答错一题扣5分,不答得0分,小玲有一道题没有答,成绩仍然不低于60分,她至少答对几道题?
解:设小玲答对的题数是x,则答错的题数是9-x,
根据题意,得10x-5(9-x)≥60,
解这个不等式,得x≥7.
答:她至少答对7道题.
巩固新知
例2 小颖准备用21元钱买笔和笔记本.已知每支笔3元,每个笔记本2.2元,她买了2个笔记本.请你帮她算一算,她还可能买几支笔?
解:设她还可能买n支笔,根据题意得
3n+2.2×2≤21,
解得 n≤ .
因为在这个问题中n只能取正整数,所以小颖还可能买1支、2支、3支、4支或5支笔.
典例精析2 一元一次不等式解答货币问题
合作探究
亮亮准备用节省的零花钱买一台复读机,他已存有45元,计划从现在起以后每月节省30元,直到他至少有300元.设x个月后他至少有300元,则符合题意的不等式是( )
A.30x-45≥300 B.30x+45≥300
C.30x-45≤300 D.30x+45≤300
B
巩固新知
例3 甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:如果购物款累计达到x元,你能用含x的式子分别表示顾客在两家商场花费的钱数吗?
典例精析3 一元一次不等式解答费用问题
合作探究
购物款 甲商场 乙商场
在甲商场购物超过100元后享受优惠,在乙商场购物超过50元后享受优惠.因此,我们需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50而不超过100元;
(3)累计购物超过100元.
当购物累计不超过50元时,甲乙消费一样.
解:
①若在甲超市花费少,则
100+0.9(x-100)<50+0.95(x-50),
得x>150 .
②若在乙超市花费少,则
100+0.9(x-100)>50+0.95(x-50),
得x<150 .
③若在甲乙超市花费一样,则
100+0.9(x-100)=50+0.95(x-50),
得x=150 .
答:购物不超过50元和刚好是150元时,在两家商场购物没有区别;超过50元而不到150元时在乙商场购物花费少;超过150元后,在甲商场购物花费少.
(3)累计购物超过100元时
解:设小明家每月用水x立方米.
∵5×1.8=9<15,
∴小明家每月用水超过5立方米,
则超出(x-5)立方米,按每立方米2元收费,列出不等式为:5×1.8+(x-5)×2≥15,
答:小明家每月用水量至少是8立方米.
小明家每月水费都不少于15元,自来水公司的收费标准如下:若每户每月用水不超过5立方米,则每立方米收费1.8元;若每户每月用水超过5立方米,则超出部分每立方米收费2元,小明家每月用水量至少是多少?
解不等式得:x≥8.
巩固新知
1.(4分)小明拿40元钱购买雪糕和矿泉水,已知每瓶矿泉水2元,每支雪糕1.5元,他买了5瓶矿泉水,x支雪糕,则所列关于x的不等式正确的是( )
A.2x+1.5×5<40 B.2x+1.5×5≤40
C.2×5+1.5x≥40 D.2×5+1.5x≤40
D
课堂练习
2.(4分)某天然气公司在一些居民小区安装天然气管道时,采用一种鼓励居民使用天然气的收费办法,若整个小区每户都安装,收整体初装费10 000元,再对每户收费500元.某小区住户按这种收费方法全部安装天然气后,每户平均支付不足1 000元,则这个小区的住户( )
A.至少20户 B.至多20户
C.至少21户 D.至多21户
C
3.(6分)(柳州中考)学校要组织去春游,小陈用50元负责购买小组所需的两种食品,买第一种食品共花去了30元,剩余的钱还要买第二种食品,已知第二种食品的单价为6元/件,问:小陈最多能买第二种食品多少件?
4.(4分)某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题?若设小明答对了x道题,则由题意可列出的不等式为( )
A.10x+5(20-x)>90 B.10x+5(20-x)<90
C.10x-5(20-x)>90 D.10x-5(20-x)<90
C
5.(4分)某人要完成2.1千米的路程,并要在18分钟内到达,已知他每分钟走90米,若跑步每分钟可跑210米,问这人完成这段路程,至少要跑多少分钟?设要跑x分钟,则由题意可列出的不等式为( )
A.210x+90(18-x)≥2 100
B.90x+210(18-x)≤2 100
C.210x+90(18-x)≥2.1
D.210x+90(18-x)>2.1
A
6.(4分)某校班级篮球联赛中,每场比赛都要分出胜负,每队胜1场得3分,负1场得1分,如果某班要在第一轮的28场比赛中至少得43分,那么这个班级至少要胜____场.
7.(6分)某部队野营训练,每小时走4千米,出发后2小时,上级有紧急通知,必须在40分钟内送到,问通讯员骑自行车至少以怎样的速度才能在40分钟内把通知送到?
8
8.(8分)(天津中考改编)某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(1)根据题意,填写下表(单位:元):
游泳次数 10 15 20 … x
方式一的总费用 150 175 200 … 100+5x
方式二的总费用 90 135 180 … 9x
(2)当x>20时,小明选择哪种付费方式更合算?并说明理由.
解:(Ⅱ)令100+5x<9x,得x>25,
令100+5x=9x,得x=25,
令100+5x>9x,得x<25,
∴当20<x<25时,小明选择方式二的付费方式更划算,
当x=25时,小明选择两种付费方式一样,
但x>25时,小明选择方式一的付费方式更划算
实际问题
设未知数
找出不等关系
列不等式
解不等式
结合实际确定答案
应用一元一次不等式解答实际问题的步骤:
归纳新知
1.某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高( )
A.40% B.33.4%
C.33.3% D.30%
B
课后练习
2.马师傅计划用10天时间加工320个零件,前两天每天加工20个零件,后改进了工作方式,结果提前一天完成了加工任务,马师傅在两天后每天至少加工____个零件.
3.(山西中考)2018年国内航空公司规定:旅客乘机时,免费携带行李箱的长、宽、高三者之和不超过115 cm.某厂家生产符合该规定的行李箱,已知行李箱的宽为20 cm,长与高的比为8∶11,则符合此规定的行李箱的高的最大值为____ cm.
40
55
4.(苏州中考)某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5 900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9 400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20 000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
5.(赤峰中考)某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话:
(1)结合两人的对话内容,求小明原计划购买文具袋多少个?
(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元.其中钢笔标价每支8元,签字笔标价每支6元,经过沟通,这次老板给予8折优惠,那么小明最多可购买钢笔多少支?
解:(1)设小明原计划购买文具袋x个,则实际购买了(x+1)个,依题意,得10(x+1)×0.85=10x-17.解得x=17.答:小明原计划购买文具袋17个
(2)设小明可购买钢笔y支,则购买签字笔(50-y)支,依题意,得[8y+6(50-y)]×80%≤400-10×17+17.解得y≤4.375.即y最大值=4.答:小明最多可购买钢笔4支
5.(南通中考)小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
次数
购买数量(件)
A B 购买总费用(元)
第一次 2 1 55
第二次 1 3 65
(2)设第三次购买商品A种a件,则购买B种商品(12-a)件,根据题意,可得a≥2(12-a),得8≤a≤12,
∵m=20a+15(12-a)=5a+180,∴当a=8时所花钱数最少,即购买A商品8件,B商品4件
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第九章 不等式与不等式组
9.2 一元一次不等式
第2课时 一元一次不等式的应用
1.掌握用一元一次不等式解决实际问题的步骤.
2.培养将实际问题向数学模型转化的能力.
3.初步认识一元一次不等式的应用价值,发展分析问题、解决问题的能力.
学习目标
小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时或11时前追上小明,速度至少应是多少
想一想
〔解析〕这是一个追赶问题,读懂题意后从路程下手找不等关系.小亮40分钟行进路程要比小明从8时20分到11时行进的路程远或二者相等才可以.这样可以得到不等式,进而解决问题.通过上述分析,你能够通过列不等式解决这个问题吗
情境导入
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
新知 一元一次不等式的应用
合作探究
前面问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h,回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 .
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
列不等式解应用题的基本步骤:
(1)审:认真审题,分清已知量、未知量;
(2)找:要抓住题中的关键字找出题中的不等关系;
(3)设:设出适当的未知数;
(4)列:根据题中的不等关系列出不等式;
(5)解:解出所列不等式的解集;
(6)答:检验是否符合题意,写出答案.
归纳小结
例1 去年广州空气质量良好(二级以上)的天数与全年
天数(365天)之比达到60%,如果到明年(365天)这样
的比值要超过70%,那么明年空气质量良好的天数要比
去年至少增加多少?
明年这样的比值要超70%
典例精析1 一元一次不等式的实际应用
分析:题目蕴含的不等关系为 ,
转 化 为 不 等 式,即 .
合作探究
解:设明年比去年空气质量良好的天数增加了 .
去年有 天空气质量良好,明年有 ,
天空气质量良好,并且 > ,
去分母,得 x + > ,
移项,合并同类项,得 x> .
由x应为正整数,得x ≥ .
答:明年要比去年空气质量良好的天数至少增加 ,
才能使这一年空气质量良好的天数超过全年天数的70% .
x天
365×60%
x+365×60%
70%
219
255.5
36.5
37
37天
在一次知识竞赛中,有10道抢答题,答对一题得10分,答错一题扣5分,不答得0分,小玲有一道题没有答,成绩仍然不低于60分,她至少答对几道题?
解:设小玲答对的题数是x,则答错的题数是9-x,
根据题意,得10x-5(9-x)≥60,
解这个不等式,得x≥7.
答:她至少答对7道题.
巩固新知
例2 小颖准备用21元钱买笔和笔记本.已知每支笔3元,每个笔记本2.2元,她买了2个笔记本.请你帮她算一算,她还可能买几支笔?
解:设她还可能买n支笔,根据题意得
3n+2.2×2≤21,
解得 n≤ .
因为在这个问题中n只能取正整数,所以小颖还可能买1支、2支、3支、4支或5支笔.
典例精析2 一元一次不等式解答货币问题
合作探究
亮亮准备用节省的零花钱买一台复读机,他已存有45元,计划从现在起以后每月节省30元,直到他至少有300元.设x个月后他至少有300元,则符合题意的不等式是( )
A.30x-45≥300 B.30x+45≥300
C.30x-45≤300 D.30x+45≤300
B
巩固新知
例3 甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:如果购物款累计达到x元,你能用含x的式子分别表示顾客在两家商场花费的钱数吗?
典例精析3 一元一次不等式解答费用问题
合作探究
购物款 甲商场 乙商场
在甲商场购物超过100元后享受优惠,在乙商场购物超过50元后享受优惠.因此,我们需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50而不超过100元;
(3)累计购物超过100元.
当购物累计不超过50元时,甲乙消费一样.
解:
①若在甲超市花费少,则
100+0.9(x-100)<50+0.95(x-50),
得x>150 .
②若在乙超市花费少,则
100+0.9(x-100)>50+0.95(x-50),
得x<150 .
③若在甲乙超市花费一样,则
100+0.9(x-100)=50+0.95(x-50),
得x=150 .
答:购物不超过50元和刚好是150元时,在两家商场购物没有区别;超过50元而不到150元时在乙商场购物花费少;超过150元后,在甲商场购物花费少.
(3)累计购物超过100元时
解:设小明家每月用水x立方米.
∵5×1.8=9<15,
∴小明家每月用水超过5立方米,
则超出(x-5)立方米,按每立方米2元收费,列出不等式为:5×1.8+(x-5)×2≥15,
答:小明家每月用水量至少是8立方米.
小明家每月水费都不少于15元,自来水公司的收费标准如下:若每户每月用水不超过5立方米,则每立方米收费1.8元;若每户每月用水超过5立方米,则超出部分每立方米收费2元,小明家每月用水量至少是多少?
解不等式得:x≥8.
巩固新知
1.(4分)小明拿40元钱购买雪糕和矿泉水,已知每瓶矿泉水2元,每支雪糕1.5元,他买了5瓶矿泉水,x支雪糕,则所列关于x的不等式正确的是( )
A.2x+1.5×5<40 B.2x+1.5×5≤40
C.2×5+1.5x≥40 D.2×5+1.5x≤40
D
课堂练习
2.(4分)某天然气公司在一些居民小区安装天然气管道时,采用一种鼓励居民使用天然气的收费办法,若整个小区每户都安装,收整体初装费10 000元,再对每户收费500元.某小区住户按这种收费方法全部安装天然气后,每户平均支付不足1 000元,则这个小区的住户( )
A.至少20户 B.至多20户
C.至少21户 D.至多21户
C
3.(6分)(柳州中考)学校要组织去春游,小陈用50元负责购买小组所需的两种食品,买第一种食品共花去了30元,剩余的钱还要买第二种食品,已知第二种食品的单价为6元/件,问:小陈最多能买第二种食品多少件?
4.(4分)某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题?若设小明答对了x道题,则由题意可列出的不等式为( )
A.10x+5(20-x)>90 B.10x+5(20-x)<90
C.10x-5(20-x)>90 D.10x-5(20-x)<90
C
5.(4分)某人要完成2.1千米的路程,并要在18分钟内到达,已知他每分钟走90米,若跑步每分钟可跑210米,问这人完成这段路程,至少要跑多少分钟?设要跑x分钟,则由题意可列出的不等式为( )
A.210x+90(18-x)≥2 100
B.90x+210(18-x)≤2 100
C.210x+90(18-x)≥2.1
D.210x+90(18-x)>2.1
A
6.(4分)某校班级篮球联赛中,每场比赛都要分出胜负,每队胜1场得3分,负1场得1分,如果某班要在第一轮的28场比赛中至少得43分,那么这个班级至少要胜____场.
7.(6分)某部队野营训练,每小时走4千米,出发后2小时,上级有紧急通知,必须在40分钟内送到,问通讯员骑自行车至少以怎样的速度才能在40分钟内把通知送到?
8
8.(8分)(天津中考改编)某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(1)根据题意,填写下表(单位:元):
游泳次数 10 15 20 … x
方式一的总费用 150 175 200 … 100+5x
方式二的总费用 90 135 180 … 9x
(2)当x>20时,小明选择哪种付费方式更合算?并说明理由.
解:(Ⅱ)令100+5x<9x,得x>25,
令100+5x=9x,得x=25,
令100+5x>9x,得x<25,
∴当20<x<25时,小明选择方式二的付费方式更划算,
当x=25时,小明选择两种付费方式一样,
但x>25时,小明选择方式一的付费方式更划算
实际问题
设未知数
找出不等关系
列不等式
解不等式
结合实际确定答案
应用一元一次不等式解答实际问题的步骤:
归纳新知
1.某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高( )
A.40% B.33.4%
C.33.3% D.30%
B
课后练习
2.马师傅计划用10天时间加工320个零件,前两天每天加工20个零件,后改进了工作方式,结果提前一天完成了加工任务,马师傅在两天后每天至少加工____个零件.
3.(山西中考)2018年国内航空公司规定:旅客乘机时,免费携带行李箱的长、宽、高三者之和不超过115 cm.某厂家生产符合该规定的行李箱,已知行李箱的宽为20 cm,长与高的比为8∶11,则符合此规定的行李箱的高的最大值为____ cm.
40
55
4.(苏州中考)某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5 900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9 400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20 000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
5.(赤峰中考)某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话:
(1)结合两人的对话内容,求小明原计划购买文具袋多少个?
(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元.其中钢笔标价每支8元,签字笔标价每支6元,经过沟通,这次老板给予8折优惠,那么小明最多可购买钢笔多少支?
解:(1)设小明原计划购买文具袋x个,则实际购买了(x+1)个,依题意,得10(x+1)×0.85=10x-17.解得x=17.答:小明原计划购买文具袋17个
(2)设小明可购买钢笔y支,则购买签字笔(50-y)支,依题意,得[8y+6(50-y)]×80%≤400-10×17+17.解得y≤4.375.即y最大值=4.答:小明最多可购买钢笔4支
5.(南通中考)小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
次数
购买数量(件)
A B 购买总费用(元)
第一次 2 1 55
第二次 1 3 65
(2)设第三次购买商品A种a件,则购买B种商品(12-a)件,根据题意,可得a≥2(12-a),得8≤a≤12,
∵m=20a+15(12-a)=5a+180,∴当a=8时所花钱数最少,即购买A商品8件,B商品4件
https://www.21cnjy.com/help/help_extract.php
