22.4圆周角（共3课时）

22.4圆周角（一）
【学习目标】
理解圆周角的定义，会识别圆周角；
掌握圆周角定理及推论.
【学习过程】
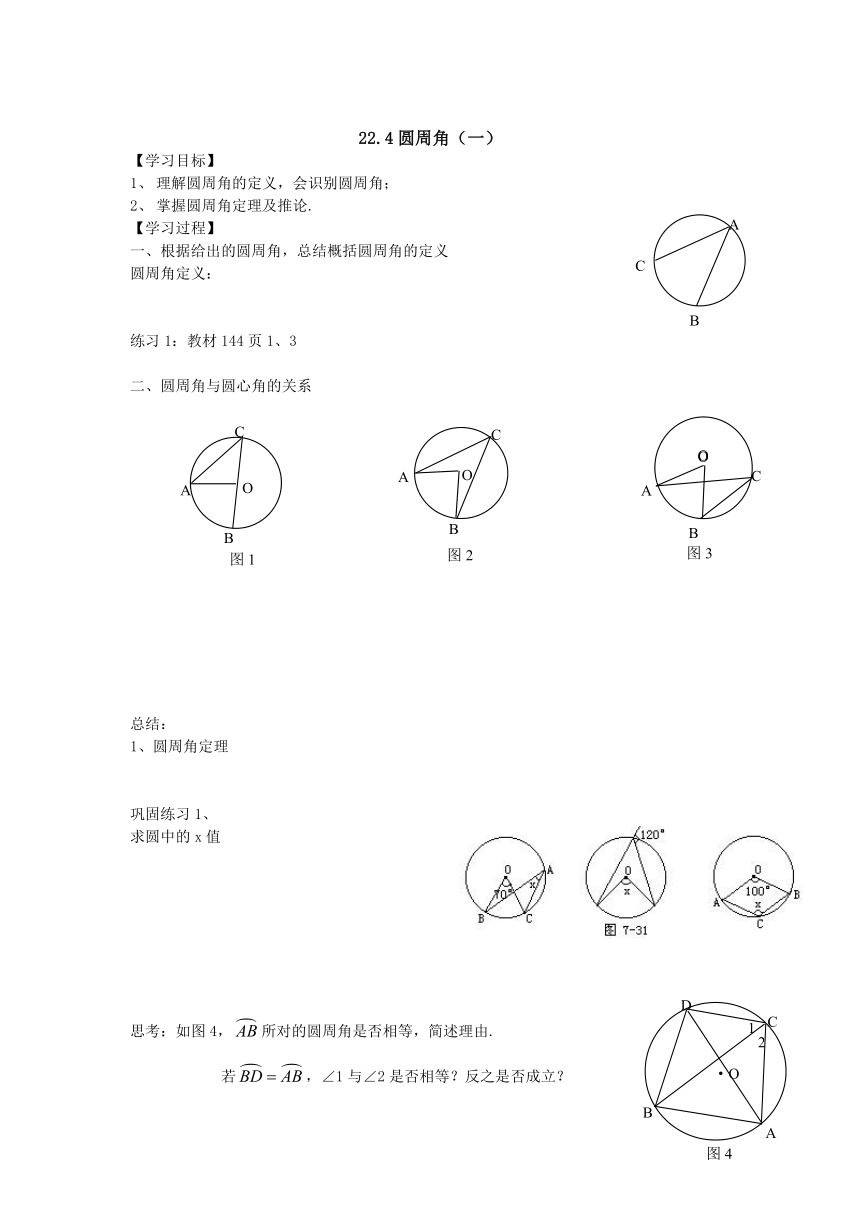
一、根据给出的圆周角，总结概括圆周角的定义
圆周角定义：
练习1：教材144页1、3
二、圆周角与圆心角的关系
总结：
1、圆周角定理
巩固练习1、
求圆中的x值
思考：如图4，所对的圆周角是否相等，简述理由.
若，∠1与∠2是否相等？反之是否成立？
2、圆周角定理推论：
符号表示：
巩固练习2：
（1）在图4 中，若，还有哪些圆周角的等量关系？
（2）如图5，指出相等的圆周角
（3）如图5，若∠CBA=∠BDC，你能得出哪些等量关系？
总结：同圆或等圆中，圆周角与所对的弧、弦之间的等量转化关系——
三、例题：
例1、如图，A、B、C、D为⊙O上的四个点，点E为DC延长线上的一点.
求证：（1）∠BCD+∠A=180°，∠ABC+∠ADC=180°；
（2）∠BCE=∠A
试一试：从上面例题，你能总结出什么结论？
圆内接四边形性质：

小结：
检测与作业：教材：146页1——4
22.4圆周角（二）
【学习目标】
进一步掌握圆周角定理及其推论
能利用推论解决有关问题
【学习过程】
一、想一想：
在⊙O中，AB为直径，如果点C是圆上（不与A、B重合），那么∠ACB具有怎样的特征？为什么？
圆周角推论2：
符号语言：
练习1：求证：如果三角形一边中线等于这边的一半，那么这个三角形是直角三角形.
二、定理及推论应用
例1、已知：如图，CD是⊙O直径，AC、AE分别交⊙O于B、D两点，∠A=23°，∠BED=21°，求∠DCE的度数.
例2、已知：如图，在⊙O中直径AB的长为10cm，弦AC的长为6cm，∠ACB的平分线交⊙O于点D，求BC、AD和BD的长.
例3、已知：⊙O中，AB为直径，∠DBA=40°，求∠DCB的度数.
例4、已知：AB为⊙O的直径，长为10cm，C在半圆上，过点C作CD⊥AB于C，且CD=4cm.
求AD、BD的长
例5、如图，A、B、C为⊙O上三点，已知∠A=45°，弦BC=5.
求⊙O的直径
练习:教材145页2
145页3．如图，⊙C经过坐标原点O，并与两坐标轴相交于A、D两点，已知∠OBA=30°，点D的坐标为（0，2），求点A的坐标及圆心C的坐标.
作业：教材147页5、6、7、8
22.4圆周角（三）
【学习目标】
1、熟练掌握圆周角定理及其推论；
2、能熟练进行角之间的转化；
3、能利用圆周角的相关结论解决相关问题.
【学习过程】
一、想一想：
观察右图，⊙O中，弦AB、ED的延长线交于A，连结EB、CD，交于点F，连结CE、BC.请找出图中的等角，并写出相似三角形
二、补充例题：
例1、如图，圆O中，弦AC与弦BD交于点P.求证：AP·PC=BP·PD
例2、⊙O的内接四边形ABCD的对角线交于P，且AB=BC.求证：AD：AB=DP:PC .
例3、如图，AB是△ABC外接圆O的直径，D为⊙O上一点，且DE⊥CD交BC于E，
求证：EB·CD＝DE·AC．
　　　　　
例4、如图，已知AB是⊙O的直径，点C是⊙O上一点，连结BC、AC，过点C作直线CD⊥AB于点D，点E是AB上一点，直线CE交⊙O于点F，连结BF，与直线CD交于点G．
求证：BC2＝BG·BF．
例5、△ABC内接于圆O，AD⊥BC于D，AB=4，AC=6，AD=3，求⊙O的半径长.
导学76——77页分类选讲
作业：教材146——147页选讲