19.1比例线段

19.1比例线段
学习目标：
1、.知道比例线段的概念.
2.、知道比例的基本性质，能进行证明和运用.
3．知道合分比性质，能进行证明。.
4、知道等比性质，能进行证明。
5、能简单运用比例的三个性质解决问题。
二、学习重点：成比例线段的定义；比例的性质及运用.
三、学习难点：比例的性质及运用.
四、学习过程：
（一）学前准备：（完成目标一）
1．已知a:b=3:2,且a-b=10，则a+b = .
2．若3，则 ； ；
3．已知，则 .
4.阅读教材104页图4-2 ，并填空：
（1）CD=2，HL=4，OA= ,
OF= BE= ,GM=
（2）,.
所以，
5. 四条线段a,b,c,d中，如果a与b的比等于c与d的比，即 （或a:b=c:d）那么这四条线段a,b,c,d叫做 ，简称 .反过来，如果四条线段a,b,c,d成比例线段，则可以记作 （或 ）.
6．线段的比是指 线段之间的比的关系，而比例线段是指 线段间的关系.
若两条线段的比 另两条线段的比，则这四条线段叫做 .
7．已知a=5,b=3,c=15，若a，b，c，x是成比例线段，则x.= .
8、 已知a、b、c、d是四条线段，它们的长度如下，试判断它们是不是成比例线段？
（1）a=16 cm b=8 cm c=5 cm d=10 cm
（2）a=8 cm b=5 cm c=6 cm d=10 cm
（3）a=1mm , b=0.8cm , c=0.02cm , d=4cm;
（二）课堂探究活动
1.通过自主探究，归纳总结出比例的基本性质，完成目标二
（1）思考 ：1：若a,b,c,d 四个数满足, 那么ad =bc 吗？与同伴交流.
根据等式的基本性质，两边同时乘以（ ）,得ad=bc,
（2）思考 2：若ad =bc (a,b,c,d都不为0），那么吗？
根据等式的基本性质，两边同时除以（ ）,得.
比例的基本性质：
【练一练】1、若3a=5b,那么a∶b=_________.
2、a∶b=4:7，那么_________.
2、通过小组合作探究，归纳总结出合比性质，完成目标三。
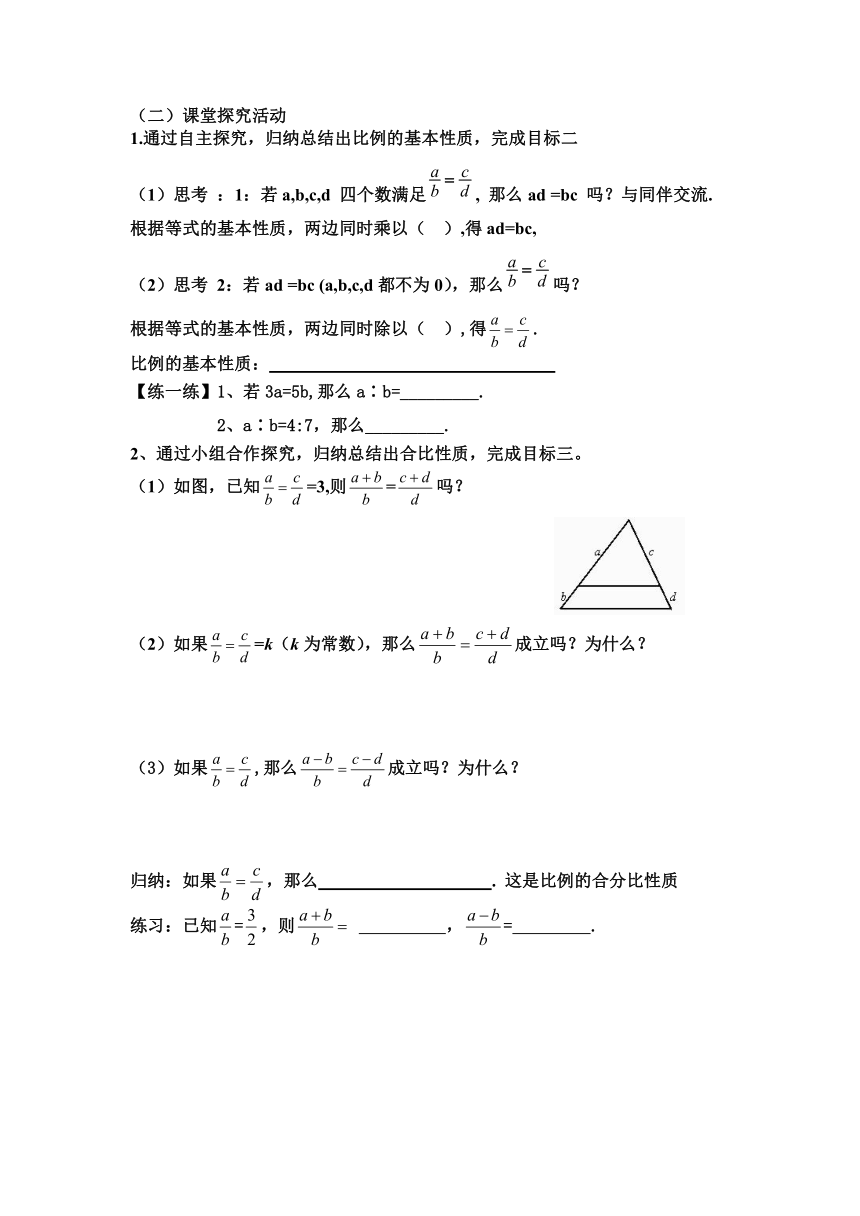
（1）如图，已知=3,则=吗？
（2）如果=k（k为常数），那么成立吗？为什么？
（3）如果,那么成立吗？为什么？
归纳：如果，那么 . 这是比例的合分比性质
练习：已知=，则 ，= .
3. 通过师生合作探究，归纳总结出等比性质，完成目标四。
（1）如果=…==k（b+d+…+n≠0）,那么=k成立吗？你能写出推理过程吗？
因此， ，这是比例的等比性质
（2）练习：如果=2，求的值
五、自我测验
1、填空
（1）若 则 ； ； ；
（2）已知 则 ； .
2、已知：==5（b+d+f≠0）
（1） （2）
3、如图，已知,且△的周长为36cm，求△的周长
六、学习收获
1、通过今天的学习，你有何收获？
2、预习中遇到困惑解决了吗？
3、你还有哪些疑惑？
七、应用与拓展
已知a，b，c都是不等于零的实数，且，求的值.