2.6 一元一次不等式组 课件(42张PPT)
文档属性
| 名称 | 2.6 一元一次不等式组 课件(42张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 09:23:47 | ||
图片预览








文档简介
(共42张PPT)
第二章 一元一次不等式与 一元一次不等式组
2.6 一元一次不等式组
·
1.理解一元一次不等式组解集的概念,掌握一元一次不等式组的解法.
2.一元一次不等式组的解集的表示,会利用数轴表示简单的一元一次不等式组的解集.
3.能够根据具体问题中的数量关系,列出一元一次不等式组解决简单的实际问题,并能根据具体问题的意义,检验结果是否合理.
·
重点:一元一次不等式组的解法,利用数轴表示简单的一
元一次不等式组的解集.
难点:利用不等式组来解决实际问题,让学生进一步感受
数形结合的作用.
一元一次不等式
公共部分
解集
无解找
小
情境引入
我90千克
我x千克
我40千克
嗨嗨,你知道我小猪大约有多重?列出不等式
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
几个同一未知数的一元一次不等式合起来就组成一元一次不等式组
下列各式哪些是一元一次不等式组,哪些不是,为什么?
(1)
(2)
x>3
x<6
(3)
4(x+5) >100
4(y-5)<68
(4)
3x-5>5x+1
(5)
-2-x≤2x-7<2+3x
(6)
≥
7.5x≤8
(1) x+40<90
(2)3x>90
你们会解这两个不等式吗 并把解集在同一坐标轴上表示出来.
x>30
x<50
在数轴上表示不等式(1), (2)的解集
0
50
30
公共部分
不等式组 的解集
X+40<90
3X>90
几个一元一次不等式的解集的公共部分,叫做一元一次不等式组的 .
解集
记作: 30D
C
②
①
动手操作:
-2 -1 0 1 2 3 4 5 6
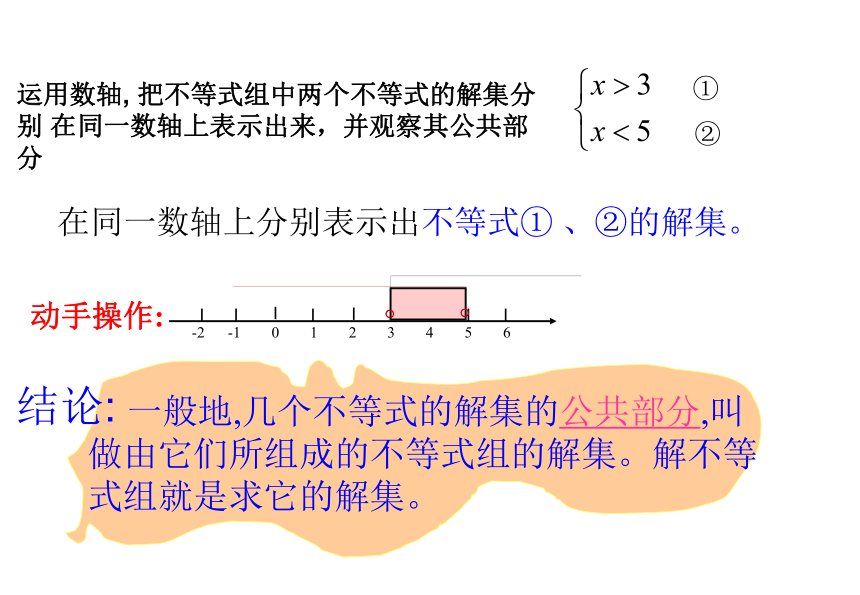
在同一数轴上分别表示出不等式① 、②的解集。
运用数轴, 把不等式组中两个不等式的解集分别 在同一数轴上表示出来,并观察其公共部分
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集。解不等式组就是求它的解集。
结论:
。
。
-1 2
不等式组的解集在数轴上表示如图,其解集是什么?
-1–2 –1 0 1 2
不等式组的解集在数轴上表示如图,其解集是什么?
–2 –1 0 1 2
不等式组无解
不等式组的解集在数轴上表示如图,其解集是什么?
–2 –1 0 1 2
不等式组的解集在数轴上表示如图,其解集是什么?
议一议: (用数轴来解释)
在① X>-1 ② X>-2 ③ X<1 ④ X <-1
X≤2 X>-1 X <2 X >1
各个一元一次不等式组中,两个不等式里X的值,
有公共部分的是: ;
没有公共部分的是: .
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
②
④
定义: 组成不等式组的各个不等式的解的公共部分就是不等式组的解.
①
③
注: 当它们没有公共部分时,则称这个不等式组无解.
一元一次不等式组的解集的确定规律
-5
-2
0
-3
-1
-4
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
小小取小
一元一次不等式组的解集的确定规律
一元一次不等式组的解集的确定规律
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小小大中间找
一元一次不等式组的解集的确定规律
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小无解了
不等式组(a>b) 数轴表示 解集 口诀
x>a 同大取大
xb无解 大大小小无解了
确定解集的方法
a
b
a
b
a
b
a
b
你能总结一下解一元一次不等式组的解题步骤吗?
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的公共部分,也就是求出了这个不等式组的解集。
1.列不等式组解应用题的一般步骤是:①审题;②设未知数;③找不等关系;④列不等式组;⑤解不等式组;⑥答。
2.利用列不等式组解应用题,其步骤与列方程组解应用题基本相同,不同的是,我们寻求的是不等关系而不是相等关系,列出的是不等式而不是等式,通常不等式组解出的结果为一解集;
3.不等式组解应用题,所求出的解不仅要适合不等式组,还必须保证实际问题具有现实意义。
应用一元一次不等式组解决实际问题的一般思路:
实际问题
不等关系
不等式
不等式组
结合实际因素
找出
列出
组成
求 解
解决
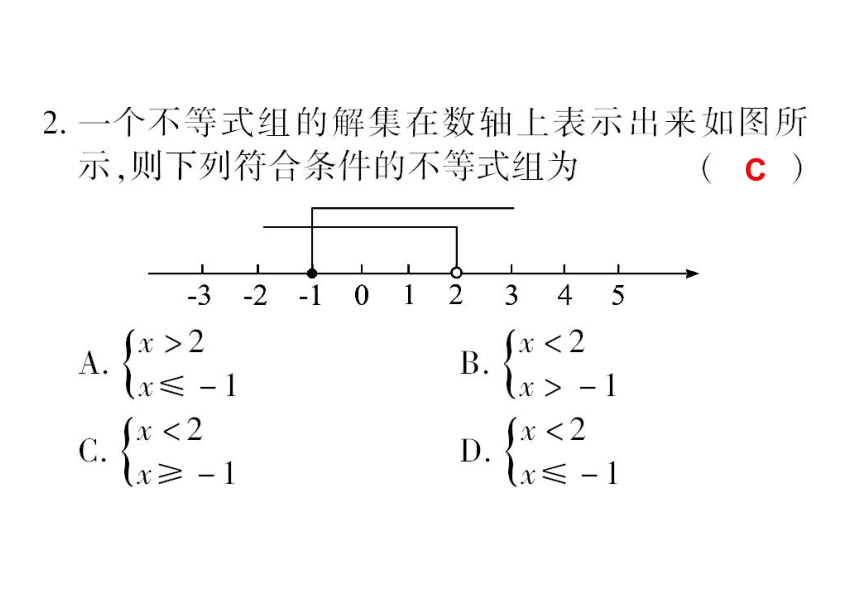
C
-1<x≤1
4
【例1】解不等式组 3x-1>2x+1①
2x>8②
解:解不等式①,得x>2
解不等式②,得x>4
在数轴上表示出①②的解集
∴原不等式组的解集为x>4
问题探讨:从练习的情况来看,请同学们认真观察它与下面几种图示的关系:①当不等号的方向一致时(称同向不等式),即:x>a x<a
x>b或 x<b.对这类不等式组可按“同大取大;同小取小”的法则,即取公共部分为它的解(如图).
②当不等号的方向相反时(称异向不等式),即:x<a
x>b 或 x>a
x<b(a>b).则若未知数的取值比大数小,比小数大时,不等式组的解集在两数之间,取公共部分(如图);
③若未知数的取值比大数还大,比小数还小,不等式组的解集是空集,即没有公共部分(如图).
【例2】解不等式组
并将解集标在数轴上
解:解不等式①得 ,解不等式 ②得x≤4,
(利用数轴确定不等式组的解集)
∴原不等式组的解集为
解析:解不等式组的基本思路是求组成这个不等式组的各个不等式的解集的公共部分,在解的过程中各个不等式彼此之间无关系,是独立的,在每一个不等式的解集都求出之后,才从“组”的角度去求“组”的解集,在此可借助于数轴用数形结合的思想去分析和解决问题.
解:解不等式①得x>-1,解不等式②得x≤1,解不等式③得x<2,
∴
∵在数轴上表示出这个解为:
∴原不等式组解集为-1<x≤1
【例3】解不等式组
解:解不等式3x-2>4x-5得:x<3,
解不等式 得x≤2,
∴
∴原不等式组解集为x≤2,
∴这个不等式组的正整数解为x=1或x=2.
【例3】解不等式组 的正整数解.
【例5】m为何整数时,方程 的解是非负数?
解析:本题综合性较强,注意审题,理解方程组的解为
非负数概念,即 .先解方程组用m的代数式表示x,
y,再运用“转化思想”,依据方程组的解集为非负数的条件列出不等式组寻求m的取值范围,最后切勿忘记确定m的整数值.
解:解方程组 得
∵方程组 的解是非负数,∴ ,
解不等式组
∴此不等式组解集为,
又∵m为整数,
∴m=3或m=4.
解法(1):原不等式相当于不等式组 ,
解不等式组得 ,
∴原不等式解集为 .
解法(2):将原不等式的两边和中间都加上1,得-2≤3x<6,将这个不等式的两边和中间都除以3得, ,∴原不等式解集为 .
【例6】解不等式-3≤3x-1<5.
【例7】用若干辆载重量为8t的汽车运一批货物,若每辆汽车只装4t,则剩下20t货物;若每辆汽车装满8t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:如果设有x辆汽车,那么这批货物共有(4x+20)t,
于是,可得 ,解这个不等式组,得5<
x<7,因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
解析:这个问题中的不等关系是货物的总质量<全部汽车载重量之和,货物的总质量>减少1辆后剩余汽车的载重量之和.
C
B
m≤3
解:(1)-1<x≤4,画数轴表示略
(2)2<x<3,画数轴表示略
(4)x>3,画数轴表示略
(3)1≤x<2,画数轴表示略
1.一元一次不等式组的概念.
2.解一元一次不等式组的步骤:
①分别求出不等式组中各个不等式的解集;
②利用数轴求出这些不等式的解集的公共部分,即这
个不等式组的解集.
3.已知一次不等式(组)的解集(特解),求其中参数的取值范围,以及解含方程与不等式的混合组中参变量(参数)取值范围,近年在各地中考卷中都有出现.求解这类问题综合性强,灵活性大,蕴含着不少的技能技巧.
第二章 一元一次不等式与 一元一次不等式组
2.6 一元一次不等式组
·
1.理解一元一次不等式组解集的概念,掌握一元一次不等式组的解法.
2.一元一次不等式组的解集的表示,会利用数轴表示简单的一元一次不等式组的解集.
3.能够根据具体问题中的数量关系,列出一元一次不等式组解决简单的实际问题,并能根据具体问题的意义,检验结果是否合理.
·
重点:一元一次不等式组的解法,利用数轴表示简单的一
元一次不等式组的解集.
难点:利用不等式组来解决实际问题,让学生进一步感受
数形结合的作用.
一元一次不等式
公共部分
解集
无解找
小
情境引入
我90千克
我x千克
我40千克
嗨嗨,你知道我小猪大约有多重?列出不等式
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
几个同一未知数的一元一次不等式合起来就组成一元一次不等式组
下列各式哪些是一元一次不等式组,哪些不是,为什么?
(1)
(2)
x>3
x<6
(3)
4(x+5) >100
4(y-5)<68
(4)
3x-5>5x+1
(5)
-2-x≤2x-7<2+3x
(6)
≥
7.5x≤8
(1) x+40<90
(2)3x>90
你们会解这两个不等式吗 并把解集在同一坐标轴上表示出来.
x>30
x<50
在数轴上表示不等式(1), (2)的解集
0
50
30
公共部分
不等式组 的解集
X+40<90
3X>90
几个一元一次不等式的解集的公共部分,叫做一元一次不等式组的 .
解集
记作: 30
C
②
①
动手操作:
-2 -1 0 1 2 3 4 5 6
在同一数轴上分别表示出不等式① 、②的解集。
运用数轴, 把不等式组中两个不等式的解集分别 在同一数轴上表示出来,并观察其公共部分
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集。解不等式组就是求它的解集。
结论:
。
。
-1 2
不等式组的解集在数轴上表示如图,其解集是什么?
-1
不等式组的解集在数轴上表示如图,其解集是什么?
–2 –1 0 1 2
不等式组无解
不等式组的解集在数轴上表示如图,其解集是什么?
–2 –1 0 1 2
不等式组的解集在数轴上表示如图,其解集是什么?
议一议: (用数轴来解释)
在① X>-1 ② X>-2 ③ X<1 ④ X <-1
X≤2 X>-1 X <2 X >1
各个一元一次不等式组中,两个不等式里X的值,
有公共部分的是: ;
没有公共部分的是: .
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
②
④
定义: 组成不等式组的各个不等式的解的公共部分就是不等式组的解.
①
③
注: 当它们没有公共部分时,则称这个不等式组无解.
一元一次不等式组的解集的确定规律
-5
-2
0
-3
-1
-4
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
小小取小
一元一次不等式组的解集的确定规律
一元一次不等式组的解集的确定规律
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小小大中间找
一元一次不等式组的解集的确定规律
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小无解了
不等式组(a>b) 数轴表示 解集 口诀
x>a 同大取大
xb
确定解集的方法
a
b
a
b
a
b
a
b
你能总结一下解一元一次不等式组的解题步骤吗?
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的公共部分,也就是求出了这个不等式组的解集。
1.列不等式组解应用题的一般步骤是:①审题;②设未知数;③找不等关系;④列不等式组;⑤解不等式组;⑥答。
2.利用列不等式组解应用题,其步骤与列方程组解应用题基本相同,不同的是,我们寻求的是不等关系而不是相等关系,列出的是不等式而不是等式,通常不等式组解出的结果为一解集;
3.不等式组解应用题,所求出的解不仅要适合不等式组,还必须保证实际问题具有现实意义。
应用一元一次不等式组解决实际问题的一般思路:
实际问题
不等关系
不等式
不等式组
结合实际因素
找出
列出
组成
求 解
解决
C
-1<x≤1
4
【例1】解不等式组 3x-1>2x+1①
2x>8②
解:解不等式①,得x>2
解不等式②,得x>4
在数轴上表示出①②的解集
∴原不等式组的解集为x>4
问题探讨:从练习的情况来看,请同学们认真观察它与下面几种图示的关系:①当不等号的方向一致时(称同向不等式),即:x>a x<a
x>b或 x<b.对这类不等式组可按“同大取大;同小取小”的法则,即取公共部分为它的解(如图).
②当不等号的方向相反时(称异向不等式),即:x<a
x>b 或 x>a
x<b(a>b).则若未知数的取值比大数小,比小数大时,不等式组的解集在两数之间,取公共部分(如图);
③若未知数的取值比大数还大,比小数还小,不等式组的解集是空集,即没有公共部分(如图).
【例2】解不等式组
并将解集标在数轴上
解:解不等式①得 ,解不等式 ②得x≤4,
(利用数轴确定不等式组的解集)
∴原不等式组的解集为
解析:解不等式组的基本思路是求组成这个不等式组的各个不等式的解集的公共部分,在解的过程中各个不等式彼此之间无关系,是独立的,在每一个不等式的解集都求出之后,才从“组”的角度去求“组”的解集,在此可借助于数轴用数形结合的思想去分析和解决问题.
解:解不等式①得x>-1,解不等式②得x≤1,解不等式③得x<2,
∴
∵在数轴上表示出这个解为:
∴原不等式组解集为-1<x≤1
【例3】解不等式组
解:解不等式3x-2>4x-5得:x<3,
解不等式 得x≤2,
∴
∴原不等式组解集为x≤2,
∴这个不等式组的正整数解为x=1或x=2.
【例3】解不等式组 的正整数解.
【例5】m为何整数时,方程 的解是非负数?
解析:本题综合性较强,注意审题,理解方程组的解为
非负数概念,即 .先解方程组用m的代数式表示x,
y,再运用“转化思想”,依据方程组的解集为非负数的条件列出不等式组寻求m的取值范围,最后切勿忘记确定m的整数值.
解:解方程组 得
∵方程组 的解是非负数,∴ ,
解不等式组
∴此不等式组解集为,
又∵m为整数,
∴m=3或m=4.
解法(1):原不等式相当于不等式组 ,
解不等式组得 ,
∴原不等式解集为 .
解法(2):将原不等式的两边和中间都加上1,得-2≤3x<6,将这个不等式的两边和中间都除以3得, ,∴原不等式解集为 .
【例6】解不等式-3≤3x-1<5.
【例7】用若干辆载重量为8t的汽车运一批货物,若每辆汽车只装4t,则剩下20t货物;若每辆汽车装满8t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:如果设有x辆汽车,那么这批货物共有(4x+20)t,
于是,可得 ,解这个不等式组,得5<
x<7,因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
解析:这个问题中的不等关系是货物的总质量<全部汽车载重量之和,货物的总质量>减少1辆后剩余汽车的载重量之和.
C
B
m≤3
解:(1)-1<x≤4,画数轴表示略
(2)2<x<3,画数轴表示略
(4)x>3,画数轴表示略
(3)1≤x<2,画数轴表示略
1.一元一次不等式组的概念.
2.解一元一次不等式组的步骤:
①分别求出不等式组中各个不等式的解集;
②利用数轴求出这些不等式的解集的公共部分,即这
个不等式组的解集.
3.已知一次不等式(组)的解集(特解),求其中参数的取值范围,以及解含方程与不等式的混合组中参变量(参数)取值范围,近年在各地中考卷中都有出现.求解这类问题综合性强,灵活性大,蕴含着不少的技能技巧.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
