4.3.2_空间两点间的距离公式
文档属性
| 名称 | 4.3.2_空间两点间的距离公式 |  | |
| 格式 | zip | ||
| 文件大小 | 190.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-10 10:07:04 | ||
图片预览






文档简介
课件17张PPT。2.3.2空间两点间的距离 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作问题提出 1. 在平面直角坐标系中两点间的距离公式是什么? 2. 在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.一、复习回顾平面内两点间的距离公式 思考:类比平面两点间距离公式的推导,你能猜想一下空间两点P1(x1,y1,z1),P2(x2,y2,z2)间的距离公式吗?O在空间直角坐标系中,任意一点P(x,y,z)到
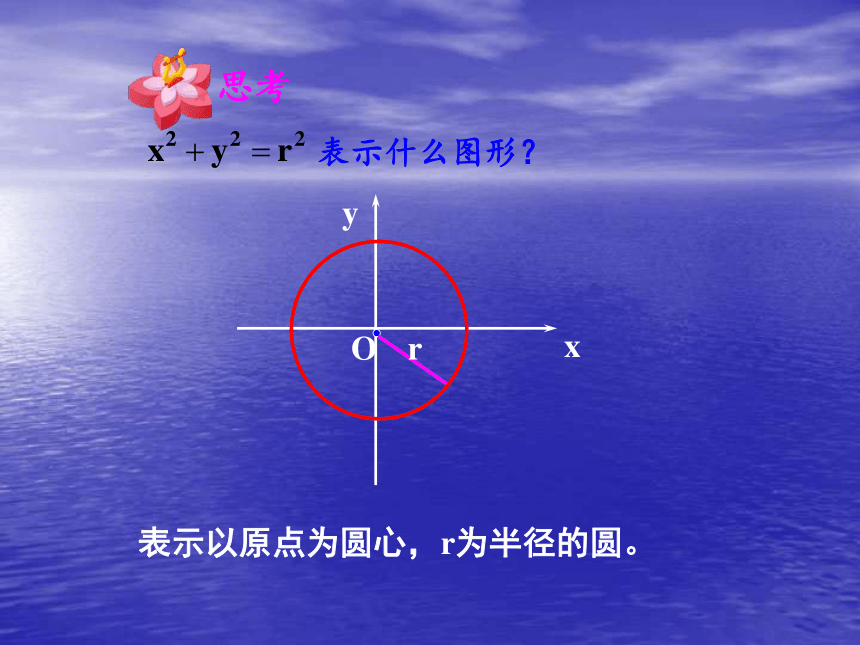
原点的距离:P`(x,y,0)二、基础知识讲解O(2) 在空间直角坐标系中,任意两点P1(x1,y1,z1)和P2(x2,y2,z2)间的距离:NMH二、基础知识讲解空间中两点P1(x1,y1,z1)和P2(x2,y2,z2)的距离公式为二、基础知识讲解公式的记忆方法:同名坐标差的平方和的算术根。思考表示什么图形?表示以原点为圆心,r为半径的圆。思考 如果|OP|是定长r,那么 表示什么图形?表示以原点为球心,r为半径的球体。例1 求空间两点A(3,-2,5 )
B(6,0,-1)的距离AB分析:利用两点间距离公式可得课堂练习1、在空间直角坐标系中,求点A、B的中点,并求出它们之间的距离:
A(2,3,5) B(3,1,4)
(2)A(6,0,1) B(3,5,7)2、在Z轴上求一点M,使点M到点A(1,0,2)与点B(1,-3,1)的距离相等。(0,0,-3)例2:在xoy平面内的直线x+y=1上确定一点M,使M到N(6,5,1)的距离最小略解:设M(x,1-x,0),利用距离公式构造出一个二次函数后求最值例题3:设A(3,3,1),B(1,-1,5),C(0,1,0),则AB的中点M到C的距离为_________分析:介绍空间直角坐标系中的中点坐标公式;M(2,1,3)已知点A(x1,y1,z1),点B(x2,y2,z2)
则线段AB中点C的坐标是课堂总结1.空间中两点P1(x1,y1,z1)和P2(x2,y2,z2)的距离公式为课后作业:
P138习题A:3,P139B :1. 1.2.解:设点M的坐标是(0,0,z)。依题意,得:解得 z=-3。
所以M点的坐标是(0,0,-3)。3.证明:根据空间两点间距离公式,得:所以 是直角三角形。4.由已知,得点N的坐标为点M的坐标为 于是
高中数学老师欧阳文丰制作问题提出 1. 在平面直角坐标系中两点间的距离公式是什么? 2. 在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.一、复习回顾平面内两点间的距离公式 思考:类比平面两点间距离公式的推导,你能猜想一下空间两点P1(x1,y1,z1),P2(x2,y2,z2)间的距离公式吗?O在空间直角坐标系中,任意一点P(x,y,z)到
原点的距离:P`(x,y,0)二、基础知识讲解O(2) 在空间直角坐标系中,任意两点P1(x1,y1,z1)和P2(x2,y2,z2)间的距离:NMH二、基础知识讲解空间中两点P1(x1,y1,z1)和P2(x2,y2,z2)的距离公式为二、基础知识讲解公式的记忆方法:同名坐标差的平方和的算术根。思考表示什么图形?表示以原点为圆心,r为半径的圆。思考 如果|OP|是定长r,那么 表示什么图形?表示以原点为球心,r为半径的球体。例1 求空间两点A(3,-2,5 )
B(6,0,-1)的距离AB分析:利用两点间距离公式可得课堂练习1、在空间直角坐标系中,求点A、B的中点,并求出它们之间的距离:
A(2,3,5) B(3,1,4)
(2)A(6,0,1) B(3,5,7)2、在Z轴上求一点M,使点M到点A(1,0,2)与点B(1,-3,1)的距离相等。(0,0,-3)例2:在xoy平面内的直线x+y=1上确定一点M,使M到N(6,5,1)的距离最小略解:设M(x,1-x,0),利用距离公式构造出一个二次函数后求最值例题3:设A(3,3,1),B(1,-1,5),C(0,1,0),则AB的中点M到C的距离为_________分析:介绍空间直角坐标系中的中点坐标公式;M(2,1,3)已知点A(x1,y1,z1),点B(x2,y2,z2)
则线段AB中点C的坐标是课堂总结1.空间中两点P1(x1,y1,z1)和P2(x2,y2,z2)的距离公式为课后作业:
P138习题A:3,P139B :1. 1.2.解:设点M的坐标是(0,0,z)。依题意,得:解得 z=-3。
所以M点的坐标是(0,0,-3)。3.证明:根据空间两点间距离公式,得:所以 是直角三角形。4.由已知,得点N的坐标为点M的坐标为 于是
