3.2.1 旋转的定义与性质 基础训练(含解析)
文档属性
| 名称 | 3.2.1 旋转的定义与性质 基础训练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 15:49:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《3.2.1旋转的定义与性质》
知识点一 旋转的定义
1.下列物体的运动不是旋转的是
A.坐在摩天轮里的小朋友
B.正在转动的时针
C.骑自行车的人
D.正在转动的风车叶片
2.如图,△ABC绕点A旋转至△ADE,则旋转角是( )
A.∠BAD
B.∠BAC
C.∠BAE
D.∠CAD
3.下列运动形式属于旋转的是( )
A.在空中上升的氢气球
B.飞驰的火车
C.时钟上钟摆的摆动
D.运动员掷出的标枪
4.观察下列图案,将它们绕其各自的中心旋转后,可与原图案重合,则这些图案的最小旋转角中最大的是( )
A.
B.
C.
D.
5.如图,△ABC是由△A'B'C'绕O点旋转180°得到的,则下列结论不成立的是( )
A.点A与点A'是对应点
B.BO=B'O
C.∠ACB=∠C'A'B'
D.AB∥A'B'
6.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE.下列结论一定正确的是( )
A.BC=BD
B.AB⊥BE
C.AC=DE
D.∠A=∠EBC
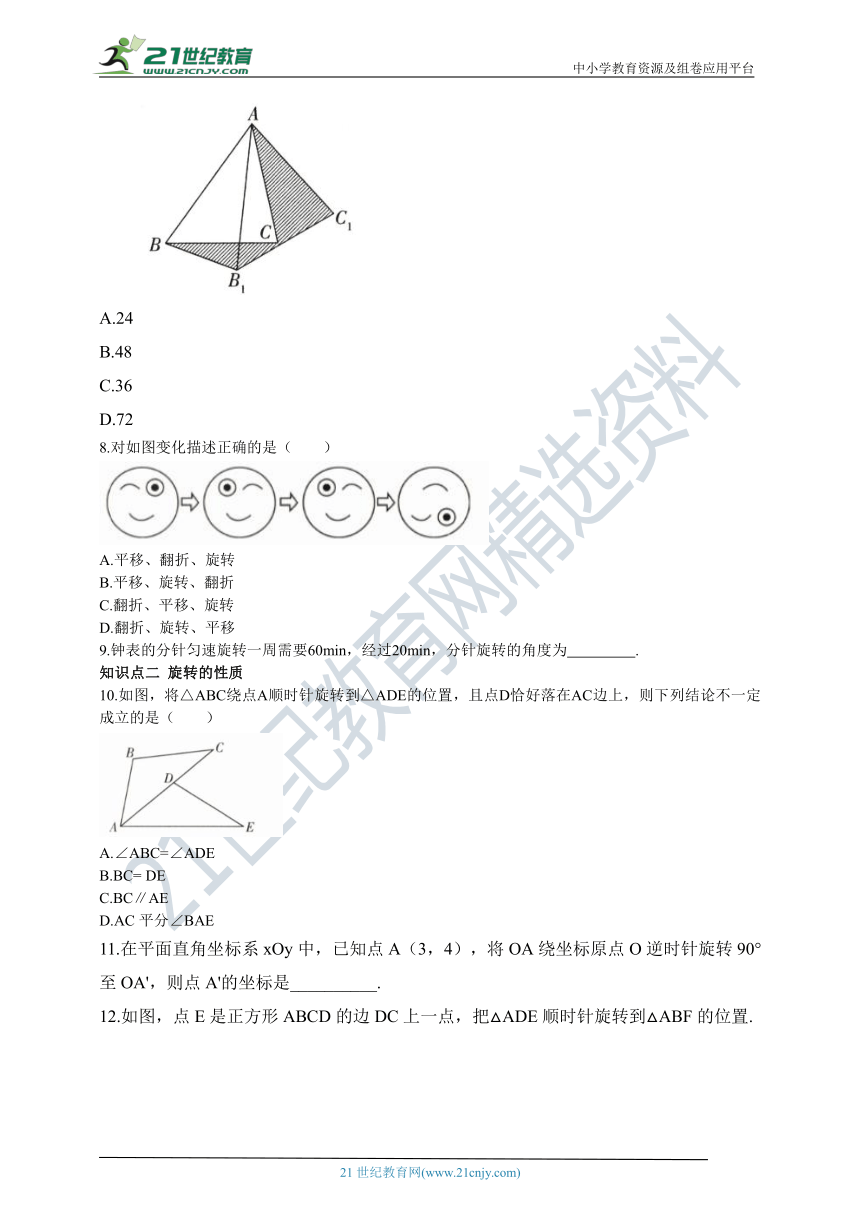
7.如图,在△ABC中,AB=12,将△ABC绕点A按逆时针方向旋转30°后得到△AB1C1,则阴影部分的面积为( )
A.24
B.48
C.36
D.72
8.对如图变化描述正确的是( )
A.平移、翻折、旋转
B.平移、旋转、翻折
C.翻折、平移、旋转
D.翻折、旋转、平移
9.钟表的分针匀速旋转一周需要60min,经过20min,分针旋转的角度为 .
知识点二 旋转的性质
10.如图,将△ABC绕点A顺时针旋转到△ADE的位置,且点D恰好落在AC边上,则下列结论不一定成立的是( )
A.∠ABC=∠ADE
B.BC= DE
C.BC∥AE
D.AC平分∠BAE
11.在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA',则点A'的坐标是__________.
12.如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转到△ABF的位置.
(1)旋转中心是点__________,旋转角是__________度;
(2)连接EF,则△AEF是__________三角形;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
13.如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P'AB,求点P与点P'之间的距离及∠APB的度数.
14.如图,△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在边AB上,则∠CAA'的度数是( )
A.50° B.70° C.110° D.120°
15.在等腰三角形ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B'处,则BB'的长度为 .
16.如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.
(1)求证:△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕着点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
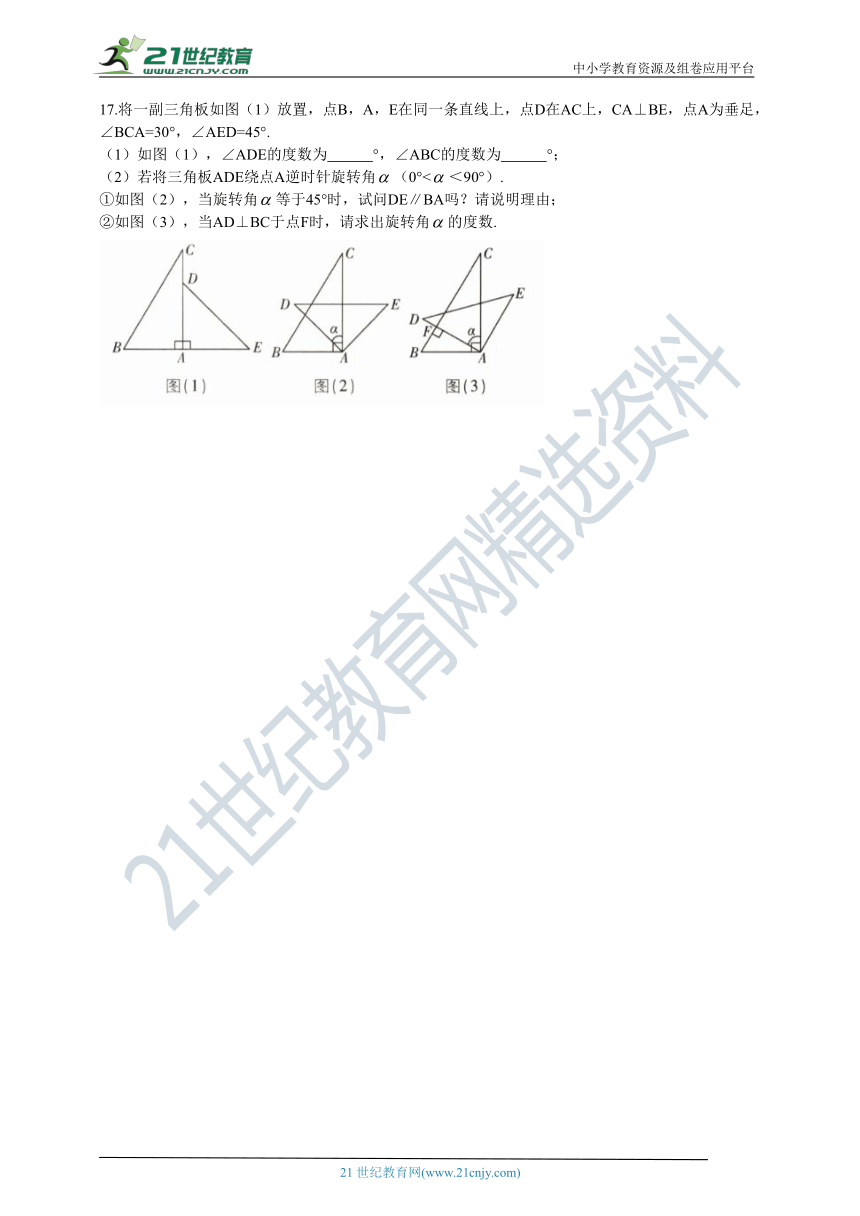
17.将一副三角板如图(1)放置,点B,A,E在同一条直线上,点D在AC上,CA⊥BE,点A为垂足,∠BCA=30°,∠AED=45°.
(1)如图(1),∠ADE的度数为 °,∠ABC的度数为 °;
(2)若将三角板ADE绕点A逆时针旋转角(0°<<90°).
①如图(2),当旋转角等于45°时,试问DE∥BA吗?请说明理由;
②如图(3),当AD⊥BC于点F时,请求出旋转角的度数.
参考答案
1.答案:C
解析:骑自行车的人在前进的过程中没有发生旋转.故选C.
2.答案:A
解析:∵△ABC绕点A旋转至△ADE,
∴旋转角为∠BAD或∠CAE,故选A.
3.答案:C
解析:由旋转的定义知C的运动形式是旋转.故选C.
4.答案:A
解析:A选项的最小旋转角为120°;B选项的最小旋转角为90°;C选项的最小旋转角是72°;D选项的最小旋转角是60°.故选A.
5.答案:C
解析:根据旋转的性质可知,∠ACB的对应角是∠A'C'B',因此C中结论不成立.故选C.
6.答案:D
解析:∵将△ABC绕点C顺时针旋转得到△DEC,
∴∠ACD=∠BCE,AC=DC,BC=EC,
∴,
∴∠A=∠EBC,故选D.
7.答案:C
解析:∵△ABC绕点A按逆时针方向旋转30°后得到△AB1C1,∴S=S,AB=AB1=12,∠BAB1=30°,∴S阴影=S,+S -S =S,作BD⊥AB1于D,在Rt中,∵∠BAB1=30°,∴BD=AB=6,∴S =AB1·BD=×12×6=36.故选C.
8.答案:C
解析:第一个图到第二个图是翻折,第二个图到第三个图是平移,第三个图到第四个图是旋转.故选C.
9.答案:120°
解析:.
10.答案:C
解析:∵将△ABC绕点A顺时针旋转到△ADE的位置,且点D恰好落在AC边上,
∴∠ABC=∠ADE,BC=DE,∠BAC=∠CAE,∴AC平分∠BAE.结论BC∥AE不一定成立.故选C.
11.答案:(-4,3)
解析:如图,过点A作AB⊥x轴于点B,过点A'作A'B'⊥x轴于点B',
由题意知OA=OA',∠AOA'=90°,
∴∠A'OB'+∠AOB=90°,
∵∠AOB+∠OAB=90°,
∴∠OAB=∠A'OB',
在△AOB和△OA'B'中,,
∴△AOB≌△OA'B'(AAS),∴OB'=AB=4,A'B'=OB=3,
∴点A'的坐标为(-4,3).
12.答案:见解析
解析:(1)A;90.
(2)等腰直角.
(3)由题意得△ADE≌△ABF,
∴S四边形AECF=S正方形ABCD=25,∴AD=5,
又∵∠D=90°,DE=2,∴AE=.
13.答案:见解析
解析:如图,连接P'P,
∵△ABC是正三角形,∴∠BAC=60°,
由旋转的性质得P'A=PA=5,P'B=PC=13,∠P'AP=∠CAB=60°,
∴△PAP'为等边三角形,
∴PP'=PA=5,即点P与点P'之间的距离为5.
在△PP'B中,PP'=5,PB=12,P'B=13,
∴PP' +PB =P'B ,
∴△BPP'为直角三角形,且∠P'PB=90°,
又∵∠P'PA=60°,
∴∠APB=∠P'PB+∠P'PA=90°+60°=150°.
14.答案:D
解析:∵∠ACB=90°,∠ABC=40°,∴∠CAB=90°-∠ABC=90°-40°=50°.∵将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C′恰好落在边AB上,∴∠A'BA=∠ABC=40°,A'B=AB,∴∠BAA'=∠BA'A=(180°-40°)=70°,∴∠CAA'=∠CAB+∠BAA′=50°+70°=120°.故选D.
15.答案:cm
解析:如图所示,在等腰直角三角形ABC中,由图形旋转的性质,知B,O,B'三点共线,且OC==1cm,则OB=cm,则BB'=2OB=cm.
16.解析:(1)在△ABC和△ADE中,
∴△ABC≌△ADE(ASA).
(2)∵△ABC≌△ADE,∴AC=AE,∴∠C=∠AEC=75°,
∴∠CAE=180°-∠C-∠AEC=30°,
∴△ADE绕着点A逆时针旋转30°后与△ABC重合,∴这个旋转角为30°.
17. 解析:(1)∠ADE的度数为45°,∠ABC的度数为60°,故答案为45,60.
(2)①DE∥BA.理由:当旋转角α等于45°时,
∵∠BAC=90°,∠α=45°,∴∠BAD=∠BAC-∠α=45°.
又∵∠ADE=45°,∴∠BAD=∠ADE,∴DE∥BA.
②∵AD⊥BC于点F,∴∠AFC=90°.
∵∠C=30°,∴∠α=180°-∠AFC-∠C=180°-90°-30°=60°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
《3.2.1旋转的定义与性质》
知识点一 旋转的定义
1.下列物体的运动不是旋转的是
A.坐在摩天轮里的小朋友
B.正在转动的时针
C.骑自行车的人
D.正在转动的风车叶片
2.如图,△ABC绕点A旋转至△ADE,则旋转角是( )
A.∠BAD
B.∠BAC
C.∠BAE
D.∠CAD
3.下列运动形式属于旋转的是( )
A.在空中上升的氢气球
B.飞驰的火车
C.时钟上钟摆的摆动
D.运动员掷出的标枪
4.观察下列图案,将它们绕其各自的中心旋转后,可与原图案重合,则这些图案的最小旋转角中最大的是( )
A.
B.
C.
D.
5.如图,△ABC是由△A'B'C'绕O点旋转180°得到的,则下列结论不成立的是( )
A.点A与点A'是对应点
B.BO=B'O
C.∠ACB=∠C'A'B'
D.AB∥A'B'
6.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE.下列结论一定正确的是( )
A.BC=BD
B.AB⊥BE
C.AC=DE
D.∠A=∠EBC
7.如图,在△ABC中,AB=12,将△ABC绕点A按逆时针方向旋转30°后得到△AB1C1,则阴影部分的面积为( )
A.24
B.48
C.36
D.72
8.对如图变化描述正确的是( )
A.平移、翻折、旋转
B.平移、旋转、翻折
C.翻折、平移、旋转
D.翻折、旋转、平移
9.钟表的分针匀速旋转一周需要60min,经过20min,分针旋转的角度为 .
知识点二 旋转的性质
10.如图,将△ABC绕点A顺时针旋转到△ADE的位置,且点D恰好落在AC边上,则下列结论不一定成立的是( )
A.∠ABC=∠ADE
B.BC= DE
C.BC∥AE
D.AC平分∠BAE
11.在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA',则点A'的坐标是__________.
12.如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转到△ABF的位置.
(1)旋转中心是点__________,旋转角是__________度;
(2)连接EF,则△AEF是__________三角形;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
13.如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P'AB,求点P与点P'之间的距离及∠APB的度数.
14.如图,△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在边AB上,则∠CAA'的度数是( )
A.50° B.70° C.110° D.120°
15.在等腰三角形ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B'处,则BB'的长度为 .
16.如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,AB=AD.
(1)求证:△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕着点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
17.将一副三角板如图(1)放置,点B,A,E在同一条直线上,点D在AC上,CA⊥BE,点A为垂足,∠BCA=30°,∠AED=45°.
(1)如图(1),∠ADE的度数为 °,∠ABC的度数为 °;
(2)若将三角板ADE绕点A逆时针旋转角(0°<<90°).
①如图(2),当旋转角等于45°时,试问DE∥BA吗?请说明理由;
②如图(3),当AD⊥BC于点F时,请求出旋转角的度数.
参考答案
1.答案:C
解析:骑自行车的人在前进的过程中没有发生旋转.故选C.
2.答案:A
解析:∵△ABC绕点A旋转至△ADE,
∴旋转角为∠BAD或∠CAE,故选A.
3.答案:C
解析:由旋转的定义知C的运动形式是旋转.故选C.
4.答案:A
解析:A选项的最小旋转角为120°;B选项的最小旋转角为90°;C选项的最小旋转角是72°;D选项的最小旋转角是60°.故选A.
5.答案:C
解析:根据旋转的性质可知,∠ACB的对应角是∠A'C'B',因此C中结论不成立.故选C.
6.答案:D
解析:∵将△ABC绕点C顺时针旋转得到△DEC,
∴∠ACD=∠BCE,AC=DC,BC=EC,
∴,
∴∠A=∠EBC,故选D.
7.答案:C
解析:∵△ABC绕点A按逆时针方向旋转30°后得到△AB1C1,∴S=S,AB=AB1=12,∠BAB1=30°,∴S阴影=S,+S -S =S,作BD⊥AB1于D,在Rt中,∵∠BAB1=30°,∴BD=AB=6,∴S =AB1·BD=×12×6=36.故选C.
8.答案:C
解析:第一个图到第二个图是翻折,第二个图到第三个图是平移,第三个图到第四个图是旋转.故选C.
9.答案:120°
解析:.
10.答案:C
解析:∵将△ABC绕点A顺时针旋转到△ADE的位置,且点D恰好落在AC边上,
∴∠ABC=∠ADE,BC=DE,∠BAC=∠CAE,∴AC平分∠BAE.结论BC∥AE不一定成立.故选C.
11.答案:(-4,3)
解析:如图,过点A作AB⊥x轴于点B,过点A'作A'B'⊥x轴于点B',
由题意知OA=OA',∠AOA'=90°,
∴∠A'OB'+∠AOB=90°,
∵∠AOB+∠OAB=90°,
∴∠OAB=∠A'OB',
在△AOB和△OA'B'中,,
∴△AOB≌△OA'B'(AAS),∴OB'=AB=4,A'B'=OB=3,
∴点A'的坐标为(-4,3).
12.答案:见解析
解析:(1)A;90.
(2)等腰直角.
(3)由题意得△ADE≌△ABF,
∴S四边形AECF=S正方形ABCD=25,∴AD=5,
又∵∠D=90°,DE=2,∴AE=.
13.答案:见解析
解析:如图,连接P'P,
∵△ABC是正三角形,∴∠BAC=60°,
由旋转的性质得P'A=PA=5,P'B=PC=13,∠P'AP=∠CAB=60°,
∴△PAP'为等边三角形,
∴PP'=PA=5,即点P与点P'之间的距离为5.
在△PP'B中,PP'=5,PB=12,P'B=13,
∴PP' +PB =P'B ,
∴△BPP'为直角三角形,且∠P'PB=90°,
又∵∠P'PA=60°,
∴∠APB=∠P'PB+∠P'PA=90°+60°=150°.
14.答案:D
解析:∵∠ACB=90°,∠ABC=40°,∴∠CAB=90°-∠ABC=90°-40°=50°.∵将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C′恰好落在边AB上,∴∠A'BA=∠ABC=40°,A'B=AB,∴∠BAA'=∠BA'A=(180°-40°)=70°,∴∠CAA'=∠CAB+∠BAA′=50°+70°=120°.故选D.
15.答案:cm
解析:如图所示,在等腰直角三角形ABC中,由图形旋转的性质,知B,O,B'三点共线,且OC==1cm,则OB=cm,则BB'=2OB=cm.
16.解析:(1)在△ABC和△ADE中,
∴△ABC≌△ADE(ASA).
(2)∵△ABC≌△ADE,∴AC=AE,∴∠C=∠AEC=75°,
∴∠CAE=180°-∠C-∠AEC=30°,
∴△ADE绕着点A逆时针旋转30°后与△ABC重合,∴这个旋转角为30°.
17. 解析:(1)∠ADE的度数为45°,∠ABC的度数为60°,故答案为45,60.
(2)①DE∥BA.理由:当旋转角α等于45°时,
∵∠BAC=90°,∠α=45°,∴∠BAD=∠BAC-∠α=45°.
又∵∠ADE=45°,∴∠BAD=∠ADE,∴DE∥BA.
②∵AD⊥BC于点F,∴∠AFC=90°.
∵∠C=30°,∴∠α=180°-∠AFC-∠C=180°-90°-30°=60°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
