3.1.2 图形的坐标变化与平移变换 基础训练(含解析)
文档属性
| 名称 | 3.1.2 图形的坐标变化与平移变换 基础训练(含解析) | 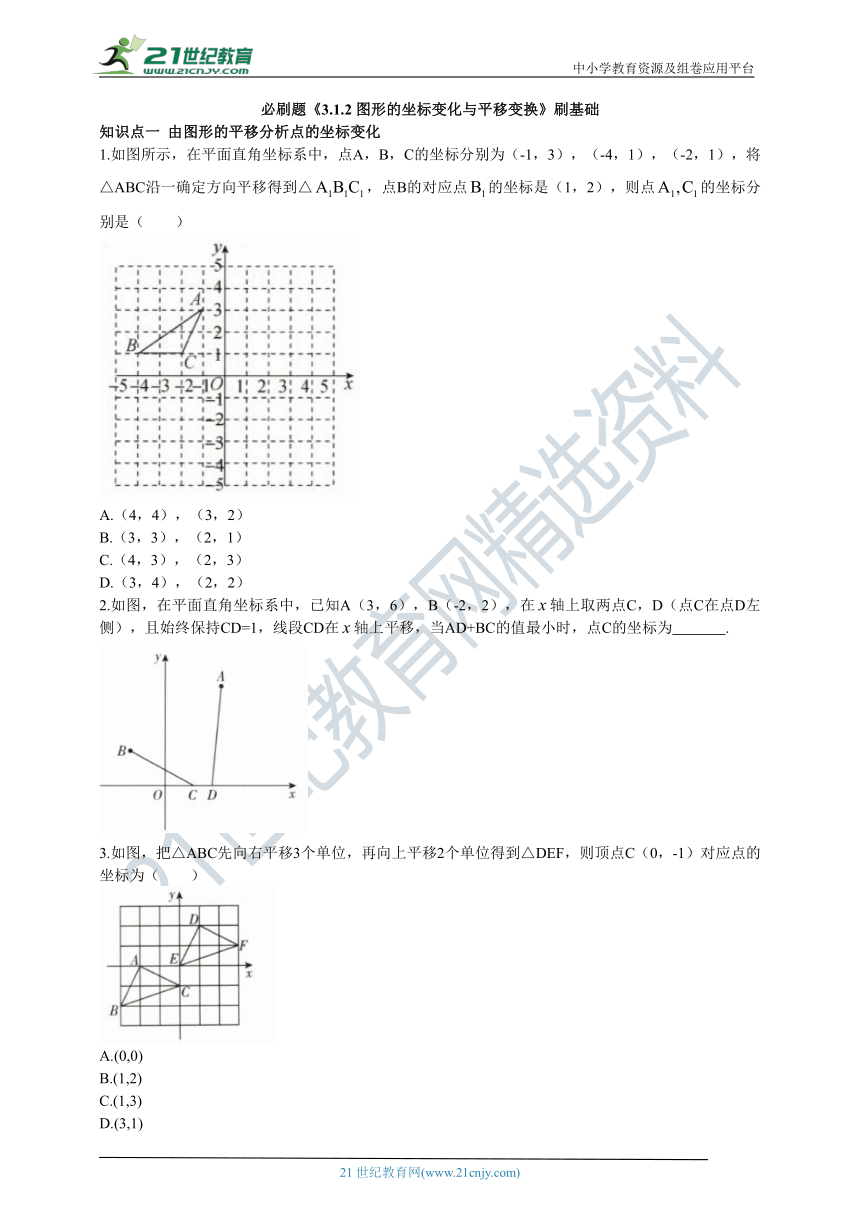 | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 15:47:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
必刷题《3.1.2图形的坐标变化与平移变换》刷基础
知识点一 由图形的平移分析点的坐标变化
1.如图所示,在平面直角坐标系中,点A,B,C的坐标分别为(-1,3),(-4,1),(-2,1),将△ABC沿一确定方向平移得到△,点B的对应点的坐标是(1,2),则点的坐标分别是( )
A.(4,4),(3,2)
B.(3,3),(2,1)
C.(4,3),(2,3)
D.(3,4),(2,2)
2.如图,在平面直角坐标系中,已知A(3,6),B(-2,2),在轴上取两点C,D(点C在点D左侧),且始终保持CD=1,线段CD在轴上平移,当AD+BC的值最小时,点C的坐标为 .
3.如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)对应点的坐标为( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
4.平面直角坐标系中,将点A(-1,2)先向左平移2个单位,再向上平移1个单位后得到的点的坐标为 .
5.如图,点A的坐标为(1,3),点B在轴上,把△OAB沿轴向右平移到△ECD,若平行四边形ABDC的面积为9,则点C的坐标为 .
6.如图,平面直角坐标系中,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至,则的值为 .
7.如图,在平面直角坐标系中,点A(0,5),B(-2,0),C(3,3),线段AB经过平移得到线段DC,其中点B的对应点为点C,点D在第一象限,直线AC交轴于点F.
(1)求点D的坐标;
(2)线段CD是由线段AB经过怎样平移得到的?
(3)求△BCF的面积.
知识点二 根据图形的平移变换作图
8.如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).将△ABC先向右平移3个单位长度,再向上平移4个单位长度得到△,在坐标系中画出△,并写出△各顶点的坐标.
9.如图,方格纸中每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后,△ABC的顶点在格点(网格线的交点)上.且A(1,-4),B(5,-3),C(4,-1).
(1)画出△ABC;
(2)将△ABC先向左平移3个单位长度,再向上平移2个单位长度,画出平移后的三角形;
(3)求出△ABC的面积.
10.如图,在平面直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(2,2).
(1)写出点A,B的坐标:A( , ),B( , );
(2)判断△ABC的形状并计算出△ABC的面积;
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',在坐标系中画出△A'B'C',并写出△A'B'C'的三个顶点坐标.
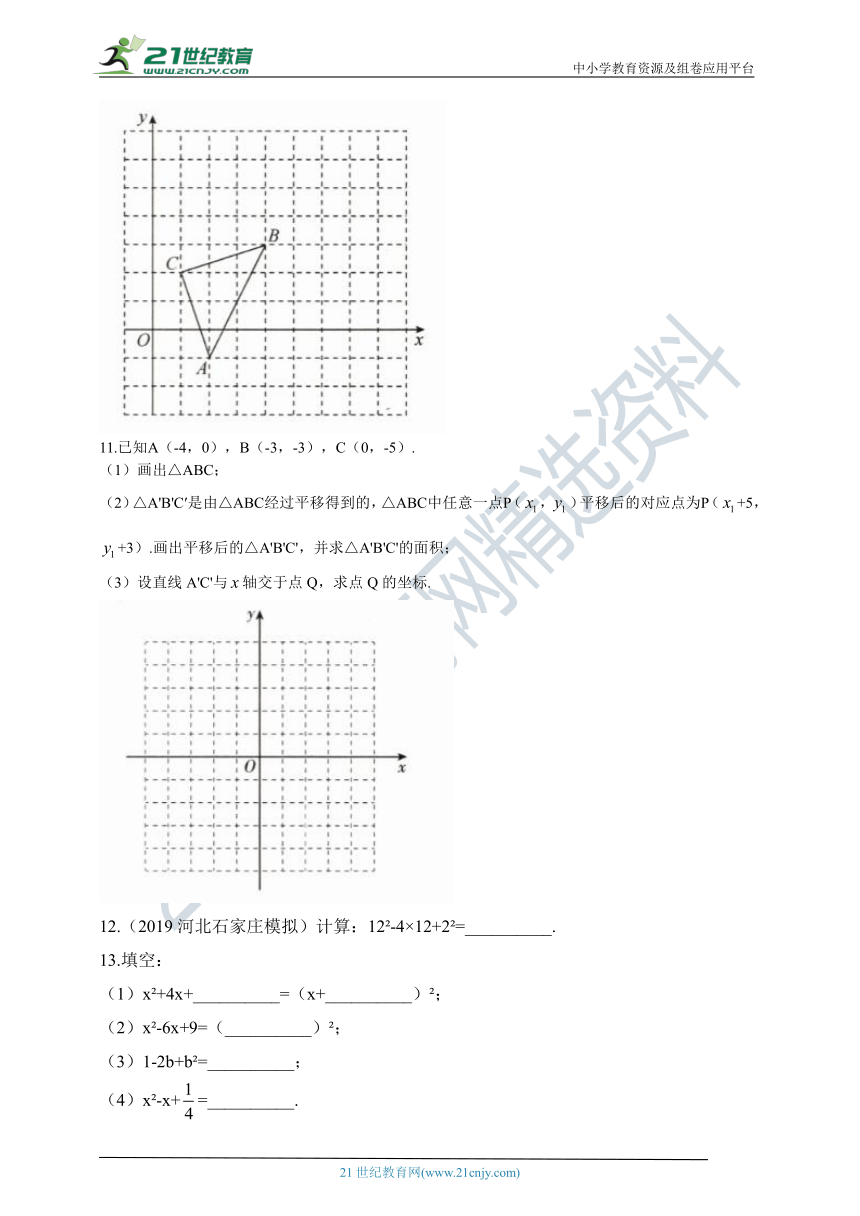
11.已知A(-4,0),B(-3,-3),C(0,-5).
(1)画出△ABC;
(2)△A'B'C′是由△ABC经过平移得到的,△ABC中任意一点P(,)平移后的对应点为P(+5,+3).画出平移后的△A'B'C',并求△A'B'C'的面积;
(3)设直线A'C'与轴交于点Q,求点Q的坐标.
12.(2019河北石家庄模拟)计算:12 -4×12+2 =__________.
13.填空:
(1)x +4x+__________=(x+__________) ;
(2)x -6x+9=(__________) ;
(3)1-2b+b =__________;
(4)x -x+=__________.
14.(2020广东高州七校摸底考试)已知4x +mx+36是完全平方式,则m的值为__________.
15.把下列各式因式分解:
(1);
(2)
(3);
(4).
参考答案
1.答案:A
解析:由点B(-4,1)的对应点的坐标是(1,2)知,需将△ABC向右平移5个单位长度,再向上平移1个单位长度,则点A(-1,3)的对应点的坐标为
(4,4),点C(-2,1)的对应点的坐标为(3,2).故选A.
2.答案:(-1,0)
解析:如图,把A(3,6)向左平移1个单位得到A'(2,6),作点B关于轴的对称点B′,连接B′A′交轴于C,在轴上取点D(点C在点D左侧),使CD=1,连接AD,则AD+BC的值最小.
∵B(-2,2),∴B'(-2,-2).
设直线B'A'的表达式为(≠0),
∴
解得
∴直线B'A'的表达式为,当时,
∴C(-1,0),
故答案为(-1,0).
3.答案:D
解析:∵把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,顶点C(0,-1),∴F(0+3,-1+2),即F(3,1),故选D.
4.答案:(-3,3)
解析:∵将点A(-1,2)先向左平移2个单位,横坐标减2,再向上平移1个单位,纵坐标加1,∴平移后得到的点的坐标为(-3,3).故答案为(-3,3).
5.答案:(4,3)
解析:∵把△OAB沿轴向右平移到△ECD,∴AC=BD,A和C的纵坐标相同.∵平行四边形ABDC的面积为9,点A的坐标为(1,3),∴3AC=9,∴AC=3,∴C(4,3),故答案为(4,3).
6.答案:2
解析:根据题意得A,B两点的坐标分别为A(2,0),B(0,1),若的坐标为(3,),的坐标为(,2),即线段AB向上平移1个单位长度,再向右平移1个单位长度,得到线段,则=0+1=1,=0+1=1,+=2.
7.解析:(1)∵点B向右平移5个单位长度,再向上平移3个单位长度得到点C,
∴点A(0,5)向右平移5个单位长度,再向上平移3个单位长度得到点D(5,8).
(2)先向右平移5个单位长度,再向上平移3个单位长度.(说法不唯一)
(3)设直线AC的表达式为(≠0),则有解得
∴直线AC的表达式为
∴点F的坐标为(,0),
∴OF=.
∵OB=2,
∴BF=,
∴
8.解析:△如图所示:
(1,3), (0,1), (2,1).
9.解析:(1)如图,△ABC即为所作.
(2)如图,△A'B'C'即为所作.
(3)△ABC的面积为.
10.解析:(1)3;-1;5;3
(2)△ABC是等腰直角三角形.∵AC=BC=,AB=,
∴AC=BC,
即△ABC是等腰直角三角形.
故△ABC的面积为5.
(3)△A'B'C'如图所示.
A'(1,0),B'(3,4),C'(0,3).
11.解析:(1)如图所示,△ABC即为所求.
(2)∵点P(,)平移后的对应点为P'(+5,+3),∴平移规律为向右平移5个单位长度,向上平移3个单位长度,∴A'(1,3),B'(2,0),C'(5,-2),则△A'B'C'如图所示.
△A'B'C'的面积为
(3)设直线A'C'的表达式为(≠0),
由题意,可得解得,
∴直线A'C'的表达式为将=0代入,可得,
∴点Q的坐标为(,0).
12.答案:100
解析:12 -4×12+2 =12 -2×2×12+2 =(12-2) =100.
13.答案:(1)4;2(2)x-3(3)(1-b) (4)
解析:(1).
(2).
(3).
(4).
14.答案:±24
解析:∵4x +mx+36=(2x) +mx+6 ,∴m=±2×2×6=±24.
15.答案:见解析
解析:(1)原式=.
(2)原式=.
(3)原式=.
(4)原式=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
必刷题《3.1.2图形的坐标变化与平移变换》刷基础
知识点一 由图形的平移分析点的坐标变化
1.如图所示,在平面直角坐标系中,点A,B,C的坐标分别为(-1,3),(-4,1),(-2,1),将△ABC沿一确定方向平移得到△,点B的对应点的坐标是(1,2),则点的坐标分别是( )
A.(4,4),(3,2)
B.(3,3),(2,1)
C.(4,3),(2,3)
D.(3,4),(2,2)
2.如图,在平面直角坐标系中,已知A(3,6),B(-2,2),在轴上取两点C,D(点C在点D左侧),且始终保持CD=1,线段CD在轴上平移,当AD+BC的值最小时,点C的坐标为 .
3.如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)对应点的坐标为( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
4.平面直角坐标系中,将点A(-1,2)先向左平移2个单位,再向上平移1个单位后得到的点的坐标为 .
5.如图,点A的坐标为(1,3),点B在轴上,把△OAB沿轴向右平移到△ECD,若平行四边形ABDC的面积为9,则点C的坐标为 .
6.如图,平面直角坐标系中,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至,则的值为 .
7.如图,在平面直角坐标系中,点A(0,5),B(-2,0),C(3,3),线段AB经过平移得到线段DC,其中点B的对应点为点C,点D在第一象限,直线AC交轴于点F.
(1)求点D的坐标;
(2)线段CD是由线段AB经过怎样平移得到的?
(3)求△BCF的面积.
知识点二 根据图形的平移变换作图
8.如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).将△ABC先向右平移3个单位长度,再向上平移4个单位长度得到△,在坐标系中画出△,并写出△各顶点的坐标.
9.如图,方格纸中每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后,△ABC的顶点在格点(网格线的交点)上.且A(1,-4),B(5,-3),C(4,-1).
(1)画出△ABC;
(2)将△ABC先向左平移3个单位长度,再向上平移2个单位长度,画出平移后的三角形;
(3)求出△ABC的面积.
10.如图,在平面直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(2,2).
(1)写出点A,B的坐标:A( , ),B( , );
(2)判断△ABC的形状并计算出△ABC的面积;
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',在坐标系中画出△A'B'C',并写出△A'B'C'的三个顶点坐标.
11.已知A(-4,0),B(-3,-3),C(0,-5).
(1)画出△ABC;
(2)△A'B'C′是由△ABC经过平移得到的,△ABC中任意一点P(,)平移后的对应点为P(+5,+3).画出平移后的△A'B'C',并求△A'B'C'的面积;
(3)设直线A'C'与轴交于点Q,求点Q的坐标.
12.(2019河北石家庄模拟)计算:12 -4×12+2 =__________.
13.填空:
(1)x +4x+__________=(x+__________) ;
(2)x -6x+9=(__________) ;
(3)1-2b+b =__________;
(4)x -x+=__________.
14.(2020广东高州七校摸底考试)已知4x +mx+36是完全平方式,则m的值为__________.
15.把下列各式因式分解:
(1);
(2)
(3);
(4).
参考答案
1.答案:A
解析:由点B(-4,1)的对应点的坐标是(1,2)知,需将△ABC向右平移5个单位长度,再向上平移1个单位长度,则点A(-1,3)的对应点的坐标为
(4,4),点C(-2,1)的对应点的坐标为(3,2).故选A.
2.答案:(-1,0)
解析:如图,把A(3,6)向左平移1个单位得到A'(2,6),作点B关于轴的对称点B′,连接B′A′交轴于C,在轴上取点D(点C在点D左侧),使CD=1,连接AD,则AD+BC的值最小.
∵B(-2,2),∴B'(-2,-2).
设直线B'A'的表达式为(≠0),
∴
解得
∴直线B'A'的表达式为,当时,
∴C(-1,0),
故答案为(-1,0).
3.答案:D
解析:∵把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,顶点C(0,-1),∴F(0+3,-1+2),即F(3,1),故选D.
4.答案:(-3,3)
解析:∵将点A(-1,2)先向左平移2个单位,横坐标减2,再向上平移1个单位,纵坐标加1,∴平移后得到的点的坐标为(-3,3).故答案为(-3,3).
5.答案:(4,3)
解析:∵把△OAB沿轴向右平移到△ECD,∴AC=BD,A和C的纵坐标相同.∵平行四边形ABDC的面积为9,点A的坐标为(1,3),∴3AC=9,∴AC=3,∴C(4,3),故答案为(4,3).
6.答案:2
解析:根据题意得A,B两点的坐标分别为A(2,0),B(0,1),若的坐标为(3,),的坐标为(,2),即线段AB向上平移1个单位长度,再向右平移1个单位长度,得到线段,则=0+1=1,=0+1=1,+=2.
7.解析:(1)∵点B向右平移5个单位长度,再向上平移3个单位长度得到点C,
∴点A(0,5)向右平移5个单位长度,再向上平移3个单位长度得到点D(5,8).
(2)先向右平移5个单位长度,再向上平移3个单位长度.(说法不唯一)
(3)设直线AC的表达式为(≠0),则有解得
∴直线AC的表达式为
∴点F的坐标为(,0),
∴OF=.
∵OB=2,
∴BF=,
∴
8.解析:△如图所示:
(1,3), (0,1), (2,1).
9.解析:(1)如图,△ABC即为所作.
(2)如图,△A'B'C'即为所作.
(3)△ABC的面积为.
10.解析:(1)3;-1;5;3
(2)△ABC是等腰直角三角形.∵AC=BC=,AB=,
∴AC=BC,
即△ABC是等腰直角三角形.
故△ABC的面积为5.
(3)△A'B'C'如图所示.
A'(1,0),B'(3,4),C'(0,3).
11.解析:(1)如图所示,△ABC即为所求.
(2)∵点P(,)平移后的对应点为P'(+5,+3),∴平移规律为向右平移5个单位长度,向上平移3个单位长度,∴A'(1,3),B'(2,0),C'(5,-2),则△A'B'C'如图所示.
△A'B'C'的面积为
(3)设直线A'C'的表达式为(≠0),
由题意,可得解得,
∴直线A'C'的表达式为将=0代入,可得,
∴点Q的坐标为(,0).
12.答案:100
解析:12 -4×12+2 =12 -2×2×12+2 =(12-2) =100.
13.答案:(1)4;2(2)x-3(3)(1-b) (4)
解析:(1).
(2).
(3).
(4).
14.答案:±24
解析:∵4x +mx+36=(2x) +mx+6 ,∴m=±2×2×6=±24.
15.答案:见解析
解析:(1)原式=.
(2)原式=.
(3)原式=.
(4)原式=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
