五年级上册数学同步拓展课件掷一掷 人教版(共14张PPT)
文档属性
| 名称 | 五年级上册数学同步拓展课件掷一掷 人教版(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 755.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 11:56:25 | ||
图片预览




文档简介
(共14张PPT)
快乐游戏 实验数学
一、游戏激趣,发现问题
游戏:老师这有一颗骰子,如果掷出3为平局,小于3就算你赢,大于3就算我赢。
想一想:同时掷两个骰子,可能出现哪些和?
1、掷出的点数和最小是( ),最大是( )。
2、掷出的点数和可能有( ),不可能有( )。
2,3,4,5,6,7,8,9,10,11,12
2,3,4,5,6,7,8,9,10,11,12
把可能出现的11个和分成A、B两组:
A组
B组
B组
A组
5,6,7,8,9
B组
A组
猜一猜:如果掷出的两数之和在A组算老师赢,如果掷出的两数之和在B组算同学们赢,哪一组赢的可能性大?你是怎么想的?
试一试:老师和同学究竟谁输谁赢?
组别 和 次数
A组 5、6、7、8、9
B组 2、3、4、10、11、12
聚焦问题:掷两枚骰子时,点数和在2—12之间,这些点数和出现的可能性大小一样吗?
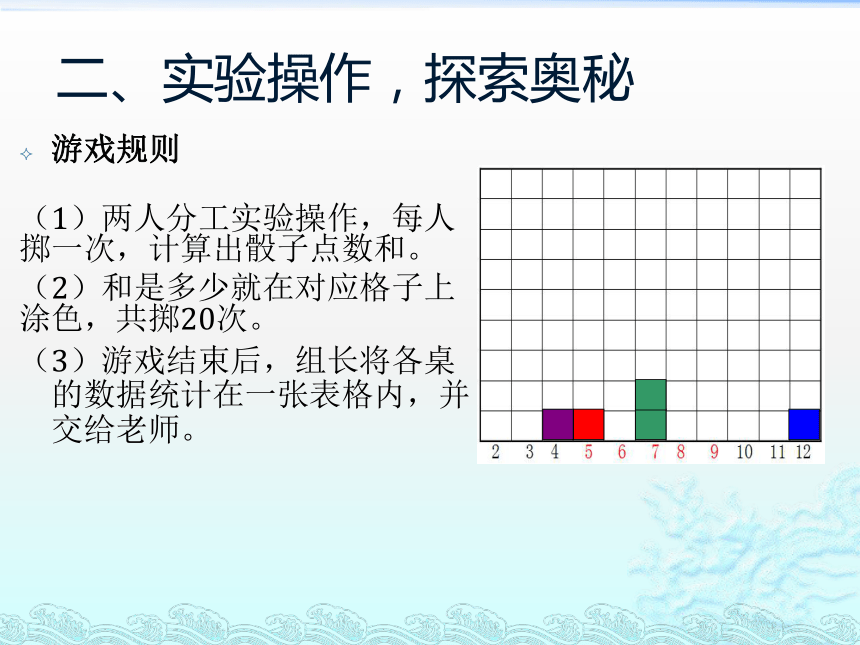
游戏规则
(1)两人分工实验操作,每人掷一次,计算出骰子点数和。
(2)和是多少就在对应格子上涂色,共掷20次。
(3)游戏结束后,组长将各桌的数据统计在一张表格内,并交给老师。
二、实验操作,探索奥秘
三、分析组成,挖掘本质
1.观察实验统计结果,你有什么新的发现?
2.想一想:为什么掷出的点数之和是A组数的可能性大一些,而点数之和是B组数的可能性小一些呢? 点数和出现的可能性与什么有关?
点数之和 2 3 4 5 骰子(红)
骰子(蓝)
1
1
1
2
1
2
1
2
3
2
3
1
1
2
3
4
4
3
2
1
把你得到的结果填在下面的列举记录表中。
观察上面的列举记录表:和是2,3,4,…,12的各有几种组合呢?请在下表中一一填出来!
和 2 3 4 5 6 7 8 9 10 11 12
组数
1
2
3
4
5
6
5
4
3
2
1
B组
B组
A组
组内交流:现在你们发现了A组能赢的秘密了吗?
四、回顾梳理,关联生活
今天我们学习了什么内容?
是怎样展开学习学习的?
通过今天的学习,你有什么收获?
◆仍然是两个骰子,怎样设定游戏规则才能使游戏公平呢?
思考:
◆如果同时掷三个骰子,朝上的三个面有三个数,它们的和可能有哪些?哪些和出现的可能性大呢?
规则:转盘上有1到6共6个数字,转两次转盘,两次数求和,如果和是5,6,7,8,9,不获奖,如果和是2,3,4,10,11,12,则获100元抵用券。
(1)如果你是组织方,想提高中奖难度,应该怎样办?
(2)如果你是消费者,要降低中奖难度,应该怎样办?
快乐游戏 实验数学
一、游戏激趣,发现问题
游戏:老师这有一颗骰子,如果掷出3为平局,小于3就算你赢,大于3就算我赢。
想一想:同时掷两个骰子,可能出现哪些和?
1、掷出的点数和最小是( ),最大是( )。
2、掷出的点数和可能有( ),不可能有( )。
2,3,4,5,6,7,8,9,10,11,12
2,3,4,5,6,7,8,9,10,11,12
把可能出现的11个和分成A、B两组:
A组
B组
B组
A组
5,6,7,8,9
B组
A组
猜一猜:如果掷出的两数之和在A组算老师赢,如果掷出的两数之和在B组算同学们赢,哪一组赢的可能性大?你是怎么想的?
试一试:老师和同学究竟谁输谁赢?
组别 和 次数
A组 5、6、7、8、9
B组 2、3、4、10、11、12
聚焦问题:掷两枚骰子时,点数和在2—12之间,这些点数和出现的可能性大小一样吗?
游戏规则
(1)两人分工实验操作,每人掷一次,计算出骰子点数和。
(2)和是多少就在对应格子上涂色,共掷20次。
(3)游戏结束后,组长将各桌的数据统计在一张表格内,并交给老师。
二、实验操作,探索奥秘
三、分析组成,挖掘本质
1.观察实验统计结果,你有什么新的发现?
2.想一想:为什么掷出的点数之和是A组数的可能性大一些,而点数之和是B组数的可能性小一些呢? 点数和出现的可能性与什么有关?
点数之和 2 3 4 5 骰子(红)
骰子(蓝)
1
1
1
2
1
2
1
2
3
2
3
1
1
2
3
4
4
3
2
1
把你得到的结果填在下面的列举记录表中。
观察上面的列举记录表:和是2,3,4,…,12的各有几种组合呢?请在下表中一一填出来!
和 2 3 4 5 6 7 8 9 10 11 12
组数
1
2
3
4
5
6
5
4
3
2
1
B组
B组
A组
组内交流:现在你们发现了A组能赢的秘密了吗?
四、回顾梳理,关联生活
今天我们学习了什么内容?
是怎样展开学习学习的?
通过今天的学习,你有什么收获?
◆仍然是两个骰子,怎样设定游戏规则才能使游戏公平呢?
思考:
◆如果同时掷三个骰子,朝上的三个面有三个数,它们的和可能有哪些?哪些和出现的可能性大呢?
规则:转盘上有1到6共6个数字,转两次转盘,两次数求和,如果和是5,6,7,8,9,不获奖,如果和是2,3,4,10,11,12,则获100元抵用券。
(1)如果你是组织方,想提高中奖难度,应该怎样办?
(2)如果你是消费者,要降低中奖难度,应该怎样办?
