北师大版七年级数学下册2.4尺规作图课件(共18张PPT)
文档属性
| 名称 | 北师大版七年级数学下册2.4尺规作图课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
第二章 相交线与平行线
§2.4尺规作图
1.在具体情境中,理解尺规作图的定
义,会用尺规作一个角等于已知角.
2.通过对角的和、差、倍的关系的分析,
能用尺规作已知角的和、差、倍.
第一环节
走进生活 引入课题
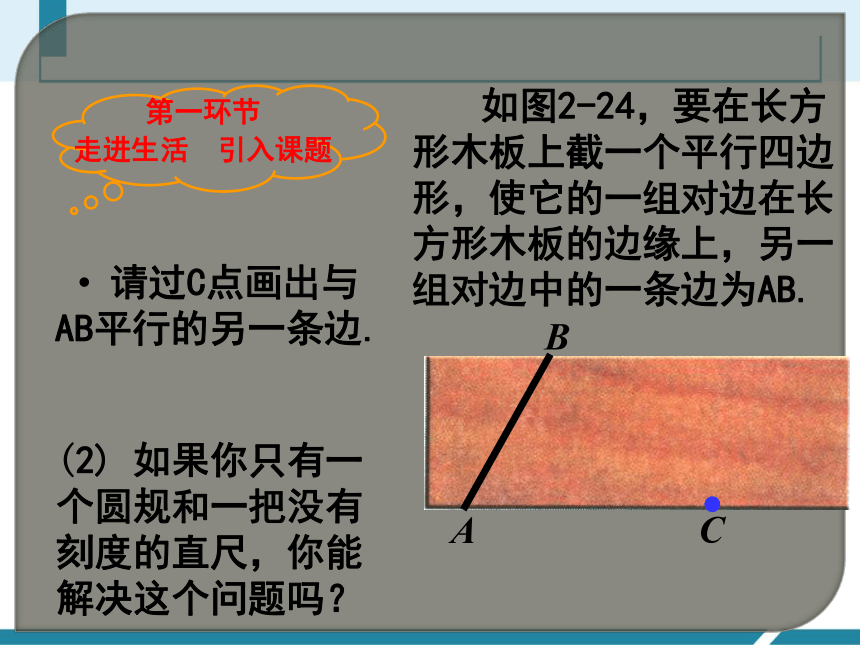
如图2-24,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB.
请过C点画出与
AB平行的另一条边.
(2) 如果你只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?
A
B
C
3.以理论形式明确规定:是欧几里得.
尺规作图
1.尺规作图:就是只准有限次地使用没有刻度
的直尺和圆规进行作图.
2.最早提出几何作图:古希腊的哲学家安那萨哥
拉斯,他因政治上的纠葛被关进监狱,并被
处死刑.在监狱里,为打发令人苦恼的生活.
他用一根绳子画圆,用破木棍、竹片作直尺,
当然这些尺上就不可能有刻度.另外,他的时
间也不多了,因此他想到要有限次地使用尺
规解决问题.
尺规作图
4.直尺的功能:
5.圆规的功能:
1801年,高斯解决了用尺规对圆周进行17等分的千年难题.欧几里得时代,已经有用尺规把圆周三等分和五等分的做法,可在以后的两千多年当中,几何学家谁也不会用尺规将圆周17等分.而高斯19岁时就解决了这一难题,轰动了当时的数学界.高斯逝世后,人们为了缅怀这位“数学家之王”,在他的墓碑上刻了一个正17边形的美丽图案.
在两点间连接一条线段;将线段向两方向延长.
以任意一点为圆心,任意长为半径作一个圆;
以任意一点为圆心,任意长为半径画一段弧.
回顾 & 思考
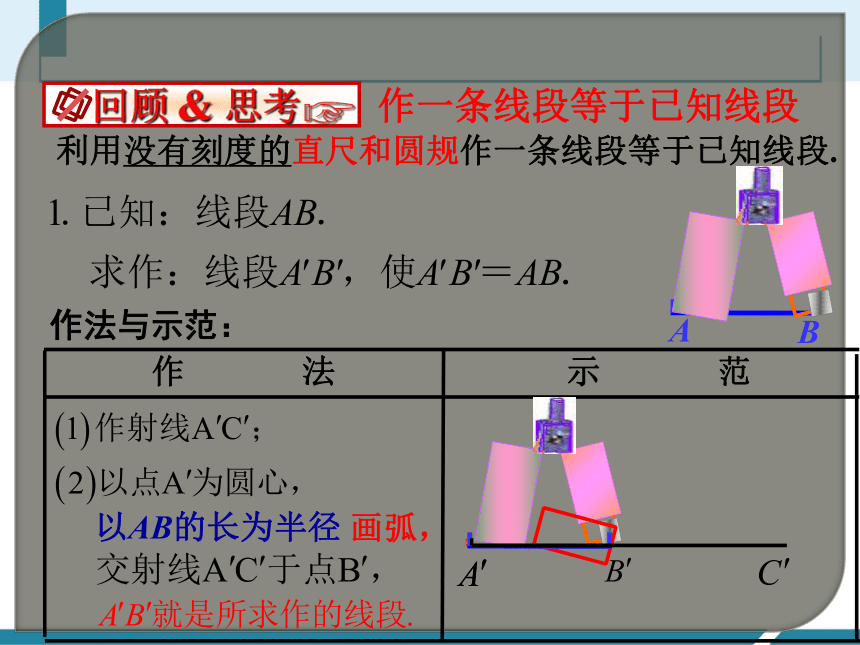
作一条线段等于已知线段
利用没有刻度的直尺和圆规作一条线段等于已知线段.
A
B
作法与示范:
示 范
作 法
以AB的长为半径
画弧,
第二环节
动手实践、探究新知
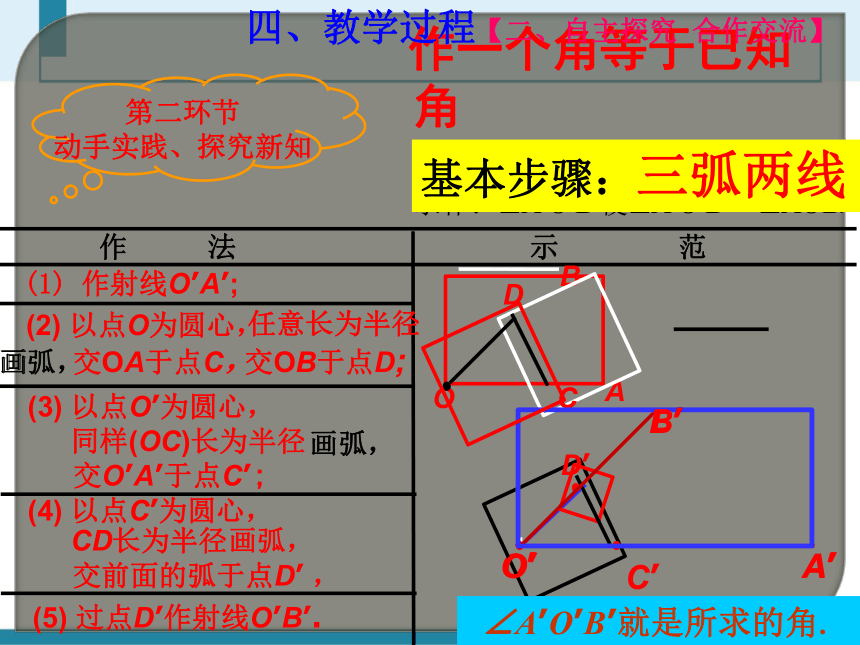
作一个角等于已知角
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
(2) 以点O为圆心,
任意长为半径
交OA于点C,
画弧,
(3) 以点O’为圆心,
同样(OC)长为半径
画弧,
(4) 以点C’为圆心,
CD长为半径
画弧,
(5) 过点D’作射线O’B’.
B
O
A
O’
A’
C
D
C’
D’
B’
A’
O’
B’
∠A’O’B’就是所求的角.
基本步骤:三弧两线
四、教学过程【二、自主探究 合作交流】
巩固练习
请用没有刻度的直尺和圆规, 在课本的图2-23中, 过点C作AB的平行线.
A
B
C
分析:若以点C为顶点作一个角∠FCE与∠BAC 相等,则∠FCE的边CF所在的直线即为所求.
E
G
G’
H
D
F
基本步骤:三弧两线
巩固练习
独立思考、合作交流;
口述作法、保留作图痕迹。
已知: ∠AOB.
利用尺规作: ∠A’O’B’,
使∠A’O’B’=2∠AOB.
B
O
A
作法一:
C
A’
B ’
∠A’OB’即为所求作的角.
B
O
A
法二:
C
D
C’
E
B’
O’
A ’
∠A’O’B’即为所求作的角.
已知:∠1,∠2,
求作:∠AOB,使得∠AOB= ∠1+∠2.
1
2
你会作两个角的和了吗?
巩固练习
巩固练习
已知:∠1,∠2,
求作:∠AOB,使得∠AOB= ∠1-∠2.
你会作两个角的差了吗?
1
2
用尺规作图比较两个角的大小.
巩固练习
B
O
A
O’
F
C
D
C’
D’
E
A’
O’
B’
第三环节
学以致用,步步为营
用尺规作下面的图形:
图案设计
第四环节
拓展延伸,综合应用
用尺规作优美的图案
右图的“邹菊图案”漂亮吗?
你想自己画出它来吗?
那就让我们从最初的步骤开始吧!
4、继续作下去,
以点O为圆心,
r 为半径作圆O;
1、
以圆O上任意一点为圆心,
r 为半径作圆,与圆O交于两点;
2、
分别以两个交点为圆心,
r 为半径作圆;
3、
在适当的区域涂上颜色.
你
作
出
美
丽
的
“
邹
菊
图
案
”
吗
?
第五环节
学有所思,反馈巩固
1. 用尺规作一个角等于已知角。
2. 用尺规作一个角等于已知角的和、差、倍。
3. 借助于已经学的用尺规作线段和角来设计图
案。
尺规作角
基本工具:
画弧必备条件:
无刻度直尺
圆规
基本步骤:三弧两线
半径
圆心
应用:
分类讨论思想
第六环节
布置作业,能力延伸
立足教育
开创未来
第二章 相交线与平行线
§2.4尺规作图
1.在具体情境中,理解尺规作图的定
义,会用尺规作一个角等于已知角.
2.通过对角的和、差、倍的关系的分析,
能用尺规作已知角的和、差、倍.
第一环节
走进生活 引入课题
如图2-24,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB.
请过C点画出与
AB平行的另一条边.
(2) 如果你只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?
A
B
C
3.以理论形式明确规定:是欧几里得.
尺规作图
1.尺规作图:就是只准有限次地使用没有刻度
的直尺和圆规进行作图.
2.最早提出几何作图:古希腊的哲学家安那萨哥
拉斯,他因政治上的纠葛被关进监狱,并被
处死刑.在监狱里,为打发令人苦恼的生活.
他用一根绳子画圆,用破木棍、竹片作直尺,
当然这些尺上就不可能有刻度.另外,他的时
间也不多了,因此他想到要有限次地使用尺
规解决问题.
尺规作图
4.直尺的功能:
5.圆规的功能:
1801年,高斯解决了用尺规对圆周进行17等分的千年难题.欧几里得时代,已经有用尺规把圆周三等分和五等分的做法,可在以后的两千多年当中,几何学家谁也不会用尺规将圆周17等分.而高斯19岁时就解决了这一难题,轰动了当时的数学界.高斯逝世后,人们为了缅怀这位“数学家之王”,在他的墓碑上刻了一个正17边形的美丽图案.
在两点间连接一条线段;将线段向两方向延长.
以任意一点为圆心,任意长为半径作一个圆;
以任意一点为圆心,任意长为半径画一段弧.
回顾 & 思考
作一条线段等于已知线段
利用没有刻度的直尺和圆规作一条线段等于已知线段.
A
B
作法与示范:
示 范
作 法
以AB的长为半径
画弧,
第二环节
动手实践、探究新知
作一个角等于已知角
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
(2) 以点O为圆心,
任意长为半径
交OA于点C,
画弧,
(3) 以点O’为圆心,
同样(OC)长为半径
画弧,
(4) 以点C’为圆心,
CD长为半径
画弧,
(5) 过点D’作射线O’B’.
B
O
A
O’
A’
C
D
C’
D’
B’
A’
O’
B’
∠A’O’B’就是所求的角.
基本步骤:三弧两线
四、教学过程【二、自主探究 合作交流】
巩固练习
请用没有刻度的直尺和圆规, 在课本的图2-23中, 过点C作AB的平行线.
A
B
C
分析:若以点C为顶点作一个角∠FCE与∠BAC 相等,则∠FCE的边CF所在的直线即为所求.
E
G
G’
H
D
F
基本步骤:三弧两线
巩固练习
独立思考、合作交流;
口述作法、保留作图痕迹。
已知: ∠AOB.
利用尺规作: ∠A’O’B’,
使∠A’O’B’=2∠AOB.
B
O
A
作法一:
C
A’
B ’
∠A’OB’即为所求作的角.
B
O
A
法二:
C
D
C’
E
B’
O’
A ’
∠A’O’B’即为所求作的角.
已知:∠1,∠2,
求作:∠AOB,使得∠AOB= ∠1+∠2.
1
2
你会作两个角的和了吗?
巩固练习
巩固练习
已知:∠1,∠2,
求作:∠AOB,使得∠AOB= ∠1-∠2.
你会作两个角的差了吗?
1
2
用尺规作图比较两个角的大小.
巩固练习
B
O
A
O’
F
C
D
C’
D’
E
A’
O’
B’
第三环节
学以致用,步步为营
用尺规作下面的图形:
图案设计
第四环节
拓展延伸,综合应用
用尺规作优美的图案
右图的“邹菊图案”漂亮吗?
你想自己画出它来吗?
那就让我们从最初的步骤开始吧!
4、继续作下去,
以点O为圆心,
r 为半径作圆O;
1、
以圆O上任意一点为圆心,
r 为半径作圆,与圆O交于两点;
2、
分别以两个交点为圆心,
r 为半径作圆;
3、
在适当的区域涂上颜色.
你
作
出
美
丽
的
“
邹
菊
图
案
”
吗
?
第五环节
学有所思,反馈巩固
1. 用尺规作一个角等于已知角。
2. 用尺规作一个角等于已知角的和、差、倍。
3. 借助于已经学的用尺规作线段和角来设计图
案。
尺规作角
基本工具:
画弧必备条件:
无刻度直尺
圆规
基本步骤:三弧两线
半径
圆心
应用:
分类讨论思想
第六环节
布置作业,能力延伸
立足教育
开创未来
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
