圆的对称性

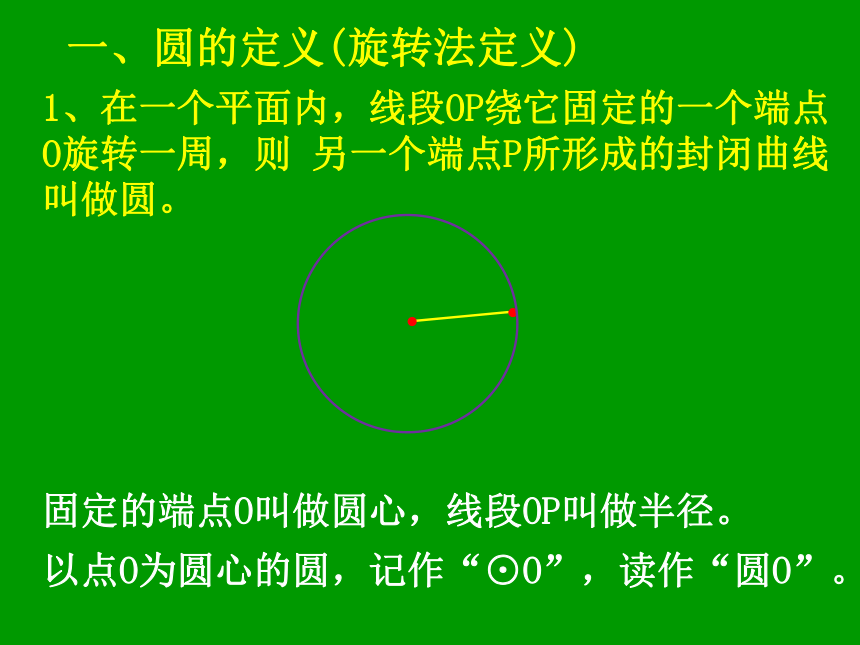
课件40张PPT。25.2 圆的对称性你能再举出一些吗?你能讲出几种形成圆的方法？1、在一个平面内，线段OP绕它固定的一个端点O旋转一周，则另一个端点P所形成的封闭曲线叫做圆。固定的端点O叫做圆心，线段OP叫做半径。以点O为圆心的圆，记作“⊙O”，读作“圆O”。一、圆的定义(旋转法定义)2.问题：到定点的距离等于定长的点又有什么特点？圆的新定义（点集法定义）：
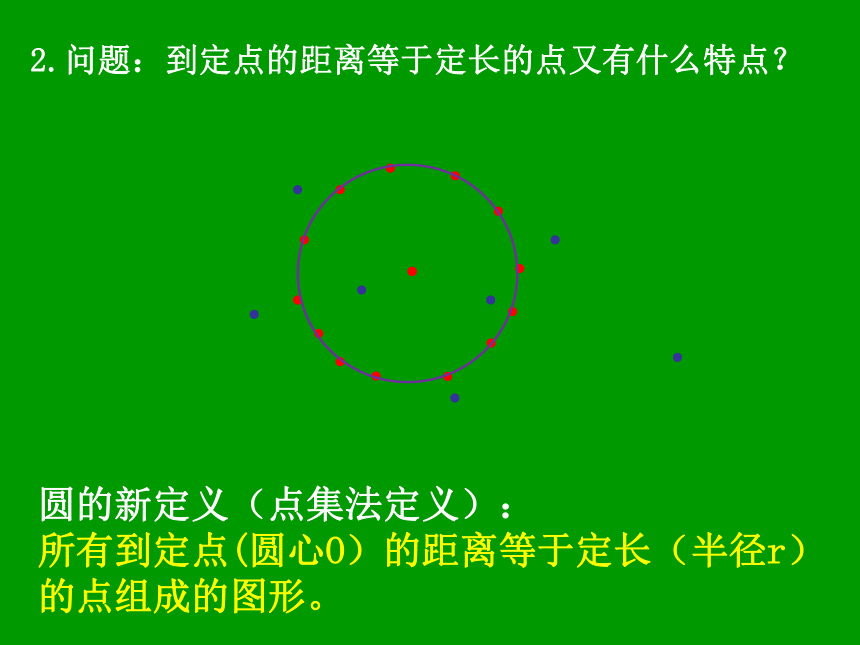
所有到定点(圆心O）的距离等于定长（半径r）的点组成的图形。思考：
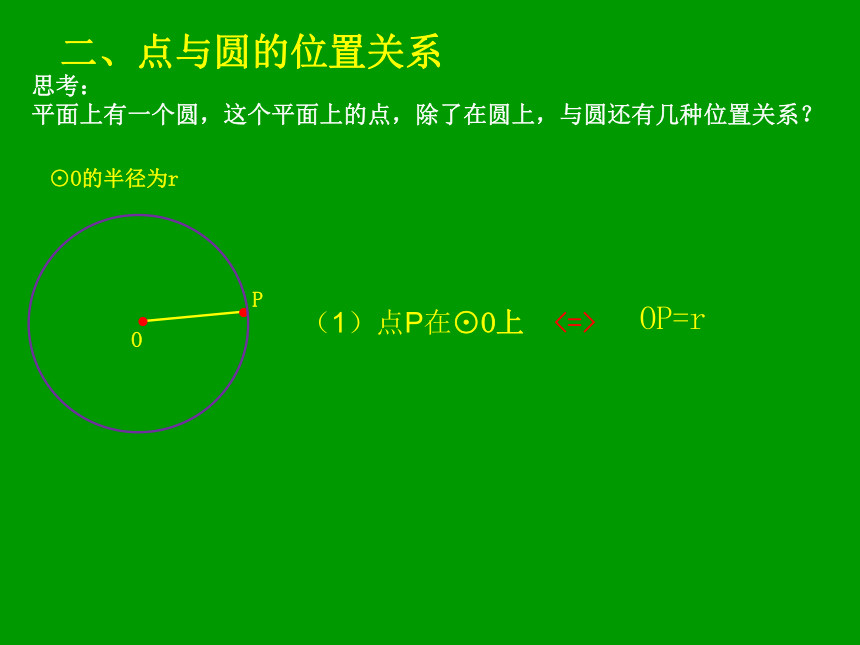
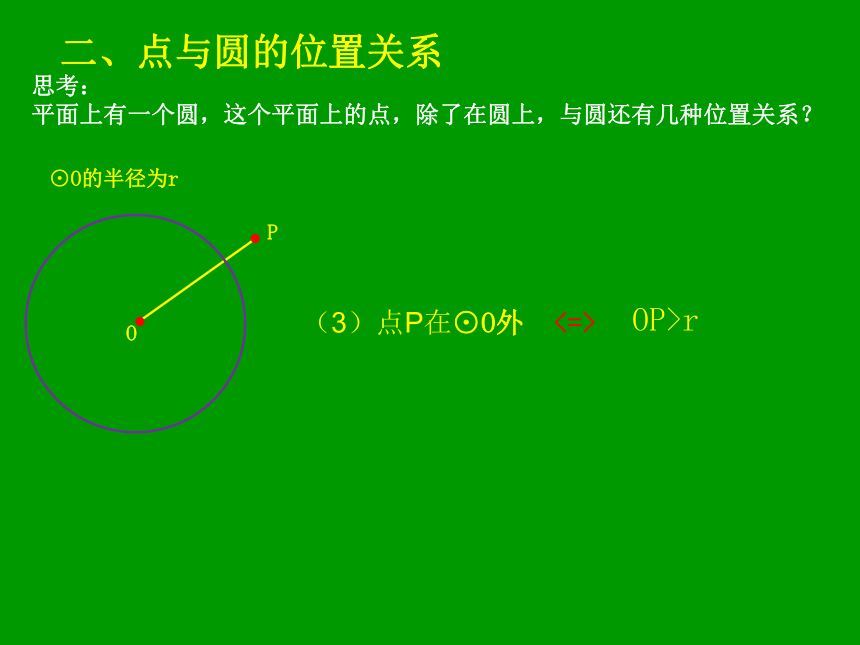
平面上有一个圆，这个平面上的点，除了在圆上，与圆还有几种位置关系？（1）点P在⊙O上<=> OP=r⊙O的半径为r二、点与圆的位置关系思考：
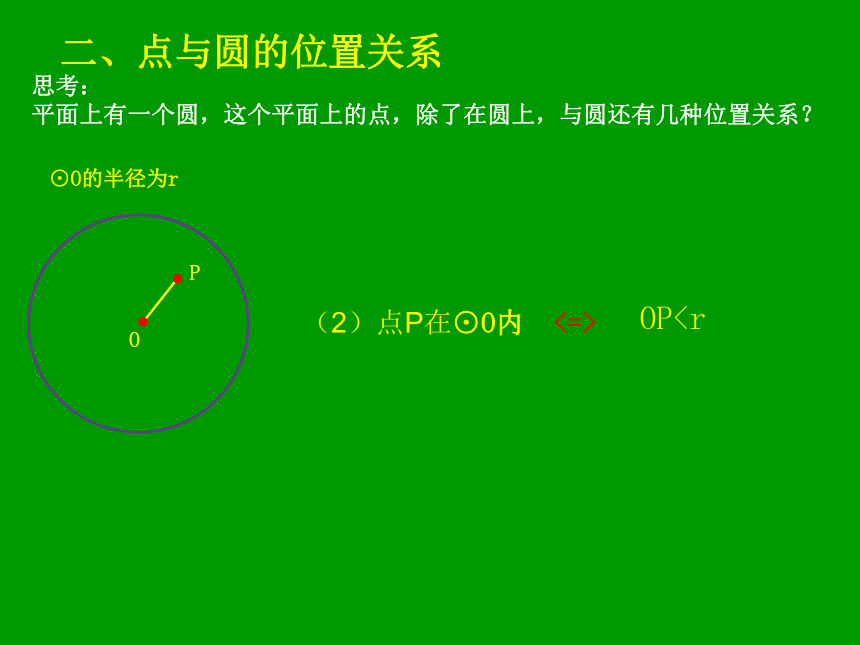
平面上有一个圆，这个平面上的点，除了在圆上，与圆还有几种位置关系？（2）点P在⊙O内<=> OP平面上有一个圆，这个平面上的点，除了在圆上，与圆还有几种位置关系？（3）点P在⊙O外<=> OP>r⊙O的半径为r二、点与圆的位置关系三、圆的相关概念1、圆上任意两点间的部分叫做圆弧,简称弧。直径的两个端点将圆分成两条弧,每一条弧
都叫做半圆。2、连接圆上任意两点间的线段叫做弦(如弦AB)。3、经过圆心弦叫做直径(如直径AC)。同圆中：半径相等，直径等于半径的2倍。4、由弦及其所对弧组成的图形叫做弓形。如图中弦AB分别与AB及ACB组成两个不同的弓形。能够重合的两个圆叫做等圆，等圆的半径相等。在同圆或等圆中，能够互相重合的弧叫做等弧。CDBA例1、已知，如图，AB、CD为⊙O的直径。求证：AD‖CB。圆是轴对称图形吗？如果是,它的对称轴是什么?你能找到多少条对称轴？你是用什么方法解决上述问题的?圆是中心对称图形吗？如果是,它的对称中心是什么?你又是用什么方法解决这个问题的?四、圆的对称性圆的对称性圆是轴对称图形.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.可利用折叠的方法即可解决上述问题.圆也是中心对称图形.它的对称中心就是圆心.用旋转的方法即可解决这个问题.求证：AE=BE垂径定理 ：
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧。AB是⊙O的一条弦，作直径CD,使CD⊥AB,垂足为E。
∟五、垂径定理AB是⊙O的一条弦,且AE=BE。过点E作直径CD.
E垂径定理的逆定理：
平分弦（不是直径）的直径垂直于弦,并且平 分弦所对的两条弧。探索思考 CD⊥AB∟ 求证例2、如图，⊙O的半径为5cm，弦AB为6cm，求圆心O到弦AB的距离。例3、赵州桥建于1400年前的隋朝，是我国石拱桥中的代表性桥梁,桥的下部呈圆弧形,桥的跨度(弧所对的弦长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，求桥所在圆的半径。（结果精确到0.1m）解得：R≈27．9（m）DCR在Rt△OAD中，由勾股定理，得即 R2=18.72+（R－7.2）2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2AB=37.4m，CD=7.2m，OD=OC－CD=R－7.21、如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．练习2、已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。你认为AC和BD有什么关系？为什么？证明：过O作OE⊥AB，垂足为E，
则AE＝BE，CE＝DE。
∴ AE－CE＝BE－DE
即 AC＝BD∟练习如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.①CD是直径,③AE=BE,②CD⊥AB,E垂直于弦的直径平分弦,并且平分弦所的两条弧.平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.①CD是直径,③AM=BM,②CD⊥AB,①②③④⑤①③②④⑤①④②③⑤①⑤②③④②③①④⑤②④①③⑤②⑤①③④③④①②⑤③⑤①②④④⑤①②③3、判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 　②平分弦的直径必垂直弦 ③垂直于弦的直径平分这条弦 ④弦的垂直平分线是圆的直径 ⑤平分弦所对的一条弧的直径必垂直这条弦 ⑥在圆中，如果一条直线经过圆心且平分弦，必平分此弦所对的弧 ⑦分别过弦的三等分点作弦的垂线，将弦所对的两条弧分别三等分 练习非直径的弦非直径的弦1、在直径是20cm的⊙O中， ∠AOB的度数是60°，那么弦AB的弦心距是　　　　　. 3、弓形的弦长为6cm，弓形的高为2cm，则这弓形所在的圆的半径为　　　　　　. 4、已知P为O内一点，且OP=2cm，如果O的半径是4cm，那么过P点的最短的弦等于 。2、在半径为30㎜的⊙O中，弦AB=36㎜，则O到AB的距离是= ，∠OAB的余弦值= 。24mm0.6例1、在直径为650mm的圆柱形油槽内装入一些
油后，油面宽AB = 600mm，求油的最大深度. DCDC└└3、如图，CD为圆O的直径，弦AB交CD于E，∠CEB=30°，DE=9㎝，CE=3㎝，求弦AB的长。练习例2、如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？如图,用AB表示桥拱，矩形EFNM表示船的横截面。AB所在圆的圆心为O，半径为r米,经过圆心O作弦AB的垂线OD，D为垂足，与AB相交于点C。根据垂径定理,D是AB的中点，C是AB的中点，CD就是拱高。例2、如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？⌒⌒⌒⌒垂径定理的推论 若圆的两条弦互相平行,那么这两条弦所夹的弧相等吗？这两条弦在圆中位置有两种情况:垂径定理的推论——圆的两条平行弦所夹的弧相等.圆的对称性及特性圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.圆也是中心对称图形,它的对称中心就是圆心.用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性OA圆心角圆心角——顶点在圆心的角(如∠AOB).如图,在⊙O中,分别作相等的圆心角∠AOB和∠A′OB′, 将其中
的一个角旋转一个角度,使得OA和O′A′重合.你能发现那些等量关系?说一说你的理由.OA’BAOB’AB=A′B′OD=O′D′如图,如果在两个等圆⊙O和⊙O′中,分别作相等的圆心角和∠AOB和∠A′O′B′,固定圆心,将其中的一个旋转一个角度,使得OA和O′A′重合.你又能发现那些等量关系?说一说你的理由.A’BAOB’O’O圆心角六、圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④OD=O′D′或和拓展与深化在同圆或等圆中,如果轮换下面四组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论?与同伴交流你的想法和理由.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′或和推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′或和 1、如图，AB、CD是⊙O的两条弦，OE、OF为AB、CD的弦心距．
（1）如果AB=CD，那么___________，_____________， ．
（2）如果 ，那么___________，_____________， ．
（3）如果∠AOB=∠COD，那么__________，_________ , ．
（4）如果OE=OF，那么___________，__________， ．
OE=OFAB=CDAB=CDAB=CDOE=OFOE=OF∠AOB=∠COD∠AOB=∠COD∠AOB=∠COD练习证明：∴AB=AC．又∠ACB=60°∴AB=BC=CA.∴∠AOB＝∠BOC＝∠AOC.ABCO例题解：∴ ∠BOD=∠COD=∠DOE=35°∴ ∠AOE=180°-3×35°
=75°练习练习再见！