2021-2022学年华东师大版八年级下册数学第16章分式单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级下册数学第16章分式单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 237.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 20:14:17 | ||
图片预览




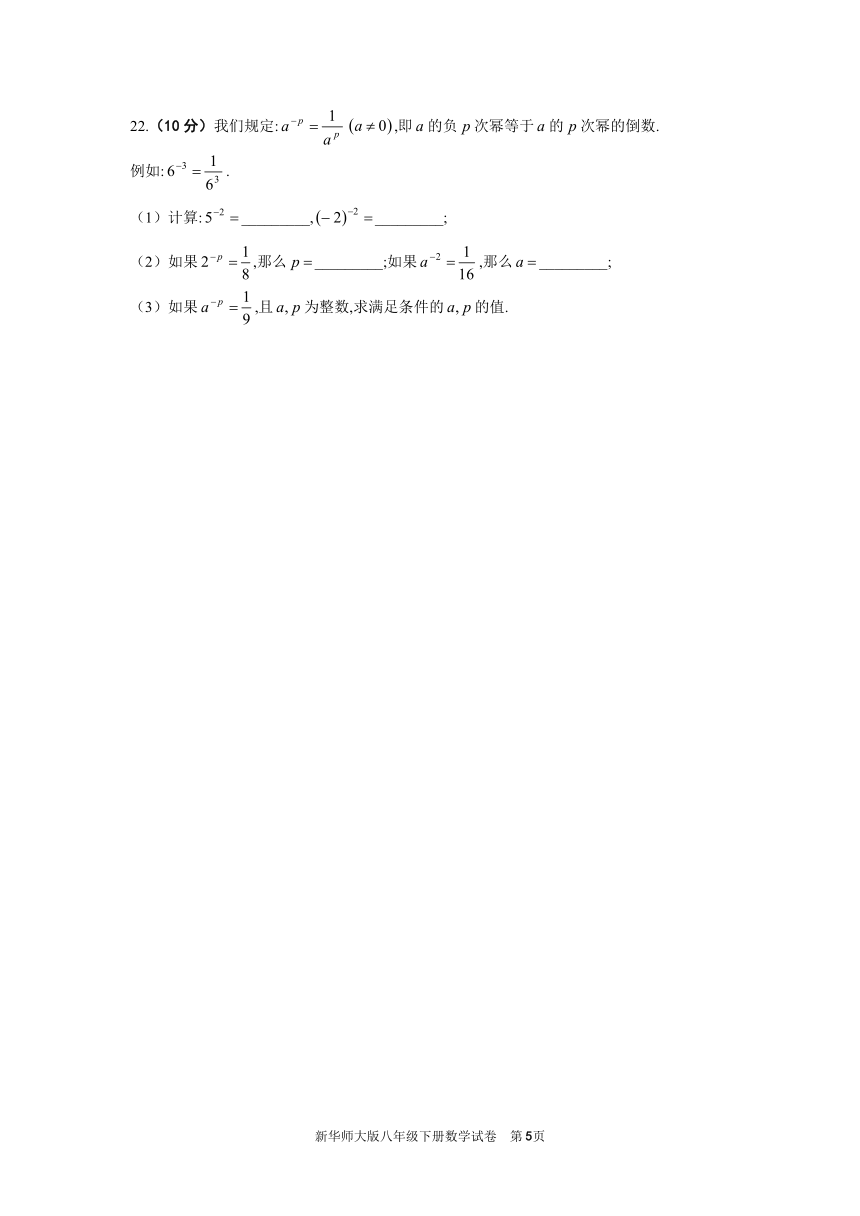
文档简介
新华师大版八年级下册数学
第16章 分式单元测试卷
姓名____________ 时间: 90分钟 满分:120分 总分____________
一、选择题(每小题3分,共30分)
1. 下列式子中分式是 【 】
(A) (B) (C) (D)
2. 如果分式有意义,则应满足的条件是 【 】
(A) (B) (C) (D)为任意实数
3. 下列等式成立的是 【 】
(A) (B)
(C) (D)
4. 计算的结果是 【 】
(A) (B) (C) (D)
5. 某种病毒的直径是0. 000 000 159米,将0. 000 000 159用科学记数法表示为 【 】
(A) (B)
(C) (D)
6. 分式中的都扩大为原来的2倍,则分式的值 【 】
(A)不变 (B)扩大2倍
(C)缩小 (D)扩大4倍
7. 若,则的大小关系是 【 】
(A) (B)
(C) (D)
8. 计算的结果是 【 】
(A) (B) (C) (D)
9. 若关于的分式方程有增根,则的值为 【 】
(A) (B) (C)5 (D)2
10. 某服装加工厂加工校服960套,原计划每天加工48套,正好按时完成.后来学校要求提前5天交货,为按时完成订单,设每天多做套,则可列方程为 【 】
(A) (B)
(C) (D)
二、填空题(每小题3分,共15分)
11. 当_________时,分式有意义.
12. 计算:_________.
13. 方程的解是_________.
14. 化简:____________.
15. 若关于的分式方程的解为正数,则的取值范围是__________.
三、解答题(共75分)
16. 计算:(每小题4分,共8分)
(1); (2).
17. 解方程:(每小题5分,共10分)
(1); (2).
18.(8分)先化简,再求值:,其中.
19.(9分)当为何值时,分式的值比分式的值大3
20.(9分)已知若关于的方程.
(1)若该分式方程有增根,求的值;
(2)若该分式方程的解为正数,求的取值范围.
21.(10分)某商店准备购进甲、乙两种商品进行销售,若甲种商品的进价比乙种商品的进价每件少6元,且用900元购进甲种商品的数量与用1000元购进乙种商品的数量相同.求甲、乙两种商品的进价每件分别是多少元
22.(10分)我们规定:,即的负次幂等于的次幂的倒数.
例如:.
(1)计算:_________,_________;
(2)如果,那么_________;如果,那么_________;
(3)如果,且为整数,求满足条件的的值.
23.(11分)例:已知,求A、B的值.
分析:这是“部分分式”问题,采用待定系数法进行求解.
解法1:
∴
解之得:.
(1)已知,则_________,_________.
(2)已知,其中是常数,求的值.
新华师大版八年级下册数学
第16章 分式单元测试卷 参考答案
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5
答案 C B B A C
题号 6 7 8 9 10
答案 A C A C D
二、填空题(每小题3分,共15分)
11. 12. 13. 14. 15. 且
新华师大版八年级下册数学试卷 第2页
三、解答题(共75分)
16. 计算:(每小题4分,共8分)
(1);
解:原式
;
(2).
解:原式
.
点评 (2)题注意运算顺序.
17. 计算:(每小题5分,共10分)
(1);
解:方程两边同时乘以得:
解这个整式方程得:
检验:把代入得:
所以是原分式方程的解;
(2).
解:
方程两边同时乘以得:
解这个整式方程得:
检验:把代入得:
所以是增根,原分式方程无解.
点评 解分式方程时一定要验根,如果出现增根,则原分式方程无解.
18.(8分)
先化简,再求值:,其中.
解:
……………………………………………5分
当时
原式.
……………………………………………8分
19.(9分)当为何值时,分式的值比分式的值大3
解:
方程两边同时乘以得:
解这个整式方程得:
检验:把代入得:
所以是原分式方程的解.
∴当时,分式的值比分式的值大3.
20.(9分)
已知若关于的方程.
(1)若该分式方程有增根,求的值;
(2)若该分式方程的解为正数,求的取值范围.
解:(1)
方程两边同时乘以得:
∴
∵该方程有增根
∴
∴;
……………………………………………4分
(2)
方程两边同时乘以得:
∴
∵该方程的解为正数
∴,解之得:
……………………………………………6分
∵,即
∴
∴
∴的取值范围是且.
……………………………………………9分
21.(10分)某商店准备购进甲、乙两种商品进行销售,若甲种商品的进价比乙种商品的进价每件少6元,且用900元购进甲种商品的数量与用1000元购进乙种商品的数量相同.求甲、乙两种商品的进价每件分别是多少元
解:(1)设甲种商品的进价为每件元,则有
……………………………………………4分
解之得:
……………………………………………7分
经检验,符合题意.
……………………………………………8分
(元)
……………………………………………9分
答:甲、乙两种商品的进价每件分别是54元、60元.
…………………………………………10分
22.(10分)我们规定:,即的负次幂等于的次幂的倒数.
例如:.
(1)计算:
_________,_________;
(2)如果,那么_________;如果,那么_________;
(3)如果,且为整数,求满足条件的的值.
解:(1),;
……………………………………………2分
(2)3 , ;
……………………………………………4分
(3)当时,;
……………………………………………6分
当时,;
……………………………………………8分
当时,.
…………………………………………10分
23.(11分)
例:已知,求A、B的值.
分析:这是“部分分式”问题,采用待定系数法进行求解.
解:
∴
解之得:.
(1)已知,则_________,_________.
(2)已知,其中是常数,求的值.
解:(1)2 , 2 ;
……………………………………………4分
(2)
∴
……………………………………………8分
解之得:.
…………………………………………11分
第16章 分式单元测试卷
姓名____________ 时间: 90分钟 满分:120分 总分____________
一、选择题(每小题3分,共30分)
1. 下列式子中分式是 【 】
(A) (B) (C) (D)
2. 如果分式有意义,则应满足的条件是 【 】
(A) (B) (C) (D)为任意实数
3. 下列等式成立的是 【 】
(A) (B)
(C) (D)
4. 计算的结果是 【 】
(A) (B) (C) (D)
5. 某种病毒的直径是0. 000 000 159米,将0. 000 000 159用科学记数法表示为 【 】
(A) (B)
(C) (D)
6. 分式中的都扩大为原来的2倍,则分式的值 【 】
(A)不变 (B)扩大2倍
(C)缩小 (D)扩大4倍
7. 若,则的大小关系是 【 】
(A) (B)
(C) (D)
8. 计算的结果是 【 】
(A) (B) (C) (D)
9. 若关于的分式方程有增根,则的值为 【 】
(A) (B) (C)5 (D)2
10. 某服装加工厂加工校服960套,原计划每天加工48套,正好按时完成.后来学校要求提前5天交货,为按时完成订单,设每天多做套,则可列方程为 【 】
(A) (B)
(C) (D)
二、填空题(每小题3分,共15分)
11. 当_________时,分式有意义.
12. 计算:_________.
13. 方程的解是_________.
14. 化简:____________.
15. 若关于的分式方程的解为正数,则的取值范围是__________.
三、解答题(共75分)
16. 计算:(每小题4分,共8分)
(1); (2).
17. 解方程:(每小题5分,共10分)
(1); (2).
18.(8分)先化简,再求值:,其中.
19.(9分)当为何值时,分式的值比分式的值大3
20.(9分)已知若关于的方程.
(1)若该分式方程有增根,求的值;
(2)若该分式方程的解为正数,求的取值范围.
21.(10分)某商店准备购进甲、乙两种商品进行销售,若甲种商品的进价比乙种商品的进价每件少6元,且用900元购进甲种商品的数量与用1000元购进乙种商品的数量相同.求甲、乙两种商品的进价每件分别是多少元
22.(10分)我们规定:,即的负次幂等于的次幂的倒数.
例如:.
(1)计算:_________,_________;
(2)如果,那么_________;如果,那么_________;
(3)如果,且为整数,求满足条件的的值.
23.(11分)例:已知,求A、B的值.
分析:这是“部分分式”问题,采用待定系数法进行求解.
解法1:
∴
解之得:.
(1)已知,则_________,_________.
(2)已知,其中是常数,求的值.
新华师大版八年级下册数学
第16章 分式单元测试卷 参考答案
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5
答案 C B B A C
题号 6 7 8 9 10
答案 A C A C D
二、填空题(每小题3分,共15分)
11. 12. 13. 14. 15. 且
新华师大版八年级下册数学试卷 第2页
三、解答题(共75分)
16. 计算:(每小题4分,共8分)
(1);
解:原式
;
(2).
解:原式
.
点评 (2)题注意运算顺序.
17. 计算:(每小题5分,共10分)
(1);
解:方程两边同时乘以得:
解这个整式方程得:
检验:把代入得:
所以是原分式方程的解;
(2).
解:
方程两边同时乘以得:
解这个整式方程得:
检验:把代入得:
所以是增根,原分式方程无解.
点评 解分式方程时一定要验根,如果出现增根,则原分式方程无解.
18.(8分)
先化简,再求值:,其中.
解:
……………………………………………5分
当时
原式.
……………………………………………8分
19.(9分)当为何值时,分式的值比分式的值大3
解:
方程两边同时乘以得:
解这个整式方程得:
检验:把代入得:
所以是原分式方程的解.
∴当时,分式的值比分式的值大3.
20.(9分)
已知若关于的方程.
(1)若该分式方程有增根,求的值;
(2)若该分式方程的解为正数,求的取值范围.
解:(1)
方程两边同时乘以得:
∴
∵该方程有增根
∴
∴;
……………………………………………4分
(2)
方程两边同时乘以得:
∴
∵该方程的解为正数
∴,解之得:
……………………………………………6分
∵,即
∴
∴
∴的取值范围是且.
……………………………………………9分
21.(10分)某商店准备购进甲、乙两种商品进行销售,若甲种商品的进价比乙种商品的进价每件少6元,且用900元购进甲种商品的数量与用1000元购进乙种商品的数量相同.求甲、乙两种商品的进价每件分别是多少元
解:(1)设甲种商品的进价为每件元,则有
……………………………………………4分
解之得:
……………………………………………7分
经检验,符合题意.
……………………………………………8分
(元)
……………………………………………9分
答:甲、乙两种商品的进价每件分别是54元、60元.
…………………………………………10分
22.(10分)我们规定:,即的负次幂等于的次幂的倒数.
例如:.
(1)计算:
_________,_________;
(2)如果,那么_________;如果,那么_________;
(3)如果,且为整数,求满足条件的的值.
解:(1),;
……………………………………………2分
(2)3 , ;
……………………………………………4分
(3)当时,;
……………………………………………6分
当时,;
……………………………………………8分
当时,.
…………………………………………10分
23.(11分)
例:已知,求A、B的值.
分析:这是“部分分式”问题,采用待定系数法进行求解.
解:
∴
解之得:.
(1)已知,则_________,_________.
(2)已知,其中是常数,求的值.
解:(1)2 , 2 ;
……………………………………………4分
(2)
∴
……………………………………………8分
解之得:.
…………………………………………11分
