2021-2022学年人教版八年级下册17.2勾股定理的逆定理课后培优(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册17.2勾股定理的逆定理课后培优(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 632.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 20:27:33 | ||
图片预览

文档简介
17.2 勾股定理的逆定理
一、单选题
1.下列各组数中,不能作为直角三角形的三边长的是( )
A.1,2, B.5,4,3 C.17,8,15 D.2,3,4
2.如图,在 4×4 的正方形网格中(每个小正方形边长均为 1),点A,B,C 在格点上,连接 AB,AC,BC,则△ABC 的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.如图①,分别以Rt△PMN(MN>NP)的三边为斜边向外作三个等腰直角三角形,再按图②的方式将两个较小的等腰直角三角形放在最大的等腰直角三角形内,则下列结论不成立的是( )
A.CF=AG
B.以EF,CD,AB为三边的三角形是直角三角形
C.AE+CG=AB
D.四边形ABDC的面积与△EFG的面积相等
4.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2 B.18cm2 C.22cm2 D.36cm2
5.若一个三角形的三边长分别为3,4,4.5,则这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
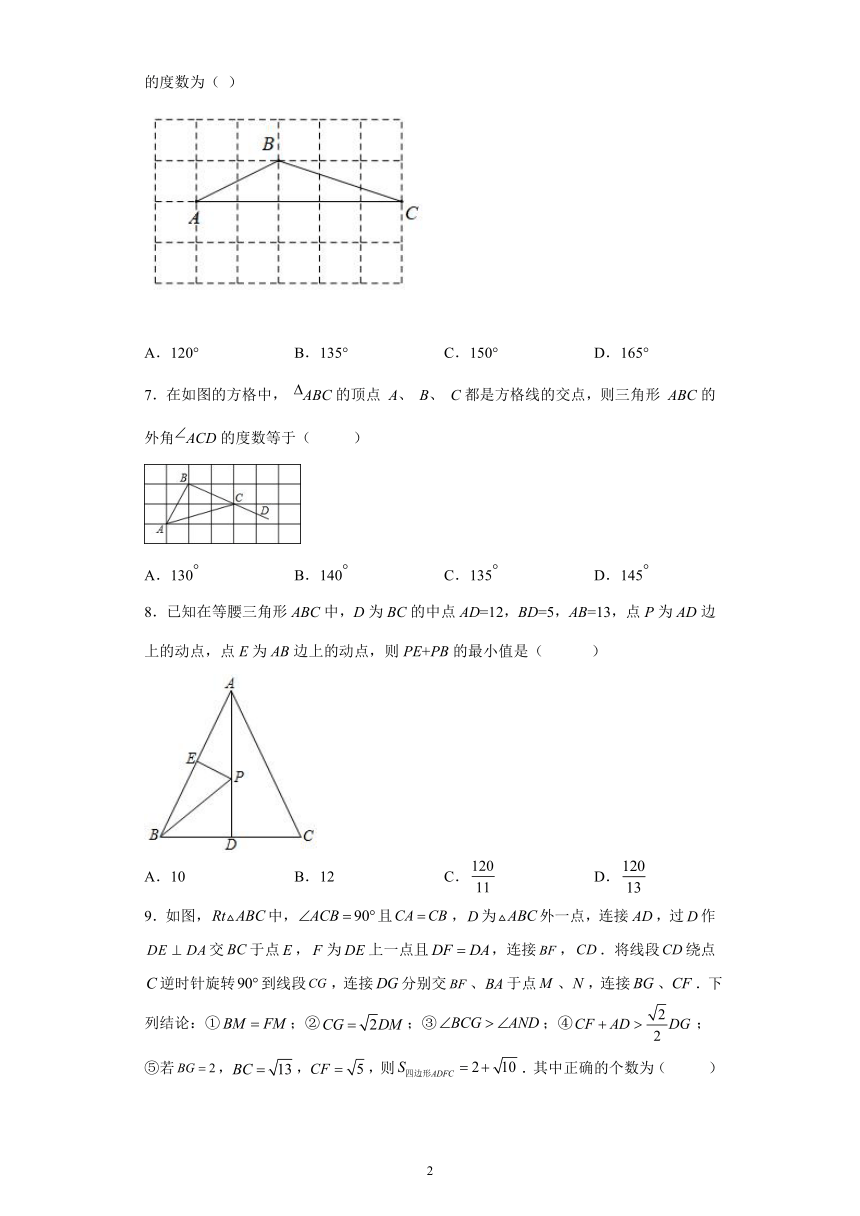
6.如图,在每个小正方形的边长为1的网格中,△ABC的的顶点都在格点上.则∠ABC的度数为( )
A.120° B.135° C.150° D.165°
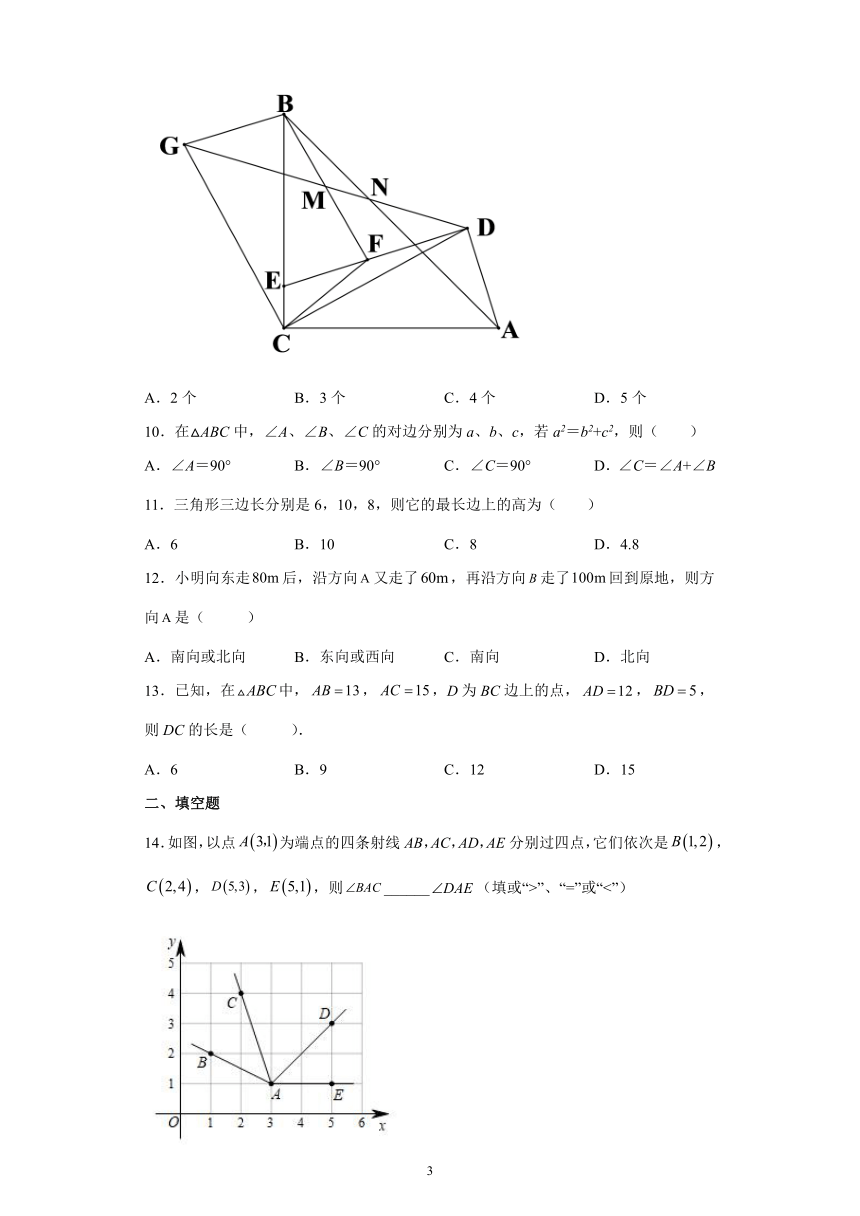
7.在如图的方格中, ABC的顶点 A、 B、 C都是方格线的交点,则三角形 ABC的外角ACD的度数等于( )
A.130 B.140 C.135 D.145
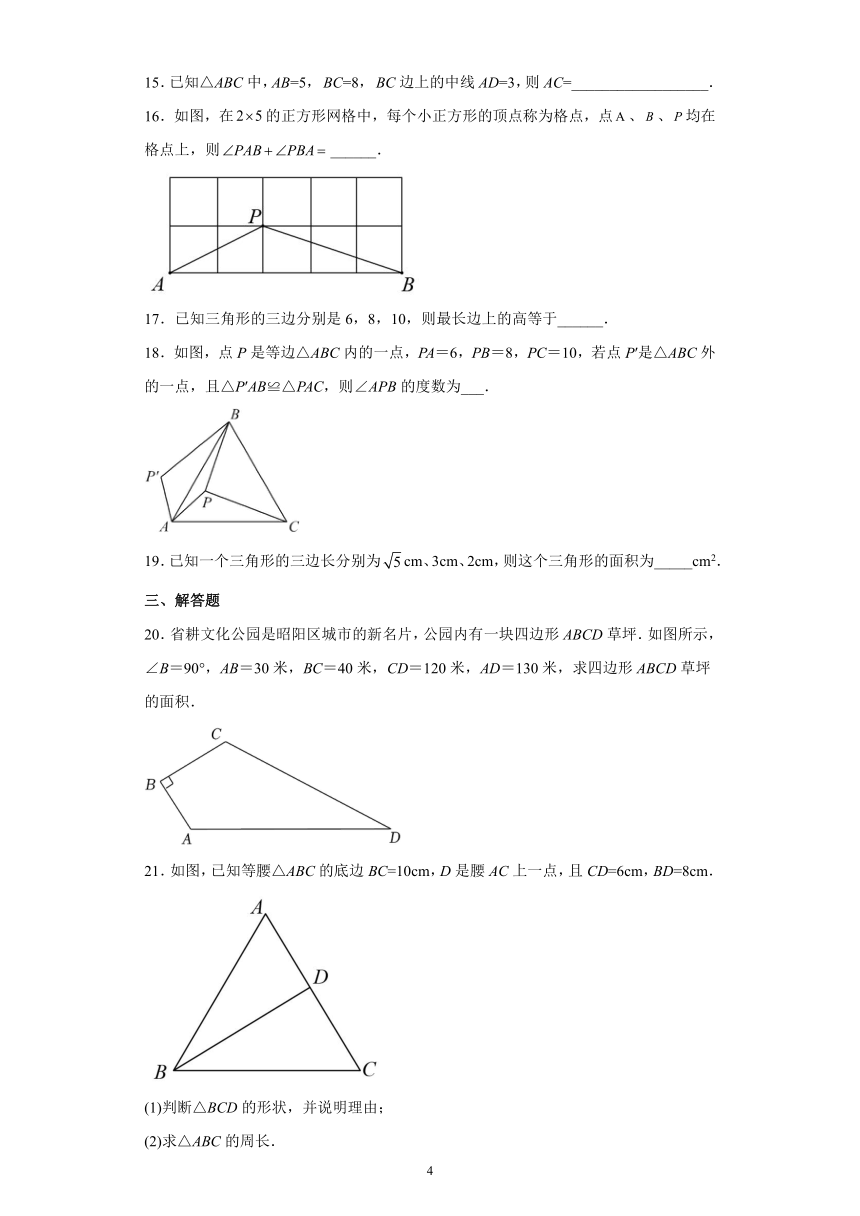
8.已知在等腰三角形ABC中,D为BC的中点AD=12,BD=5,AB=13,点P为AD边上的动点,点E为AB边上的动点,则PE+PB的最小值是( )
A.10 B.12 C. D.
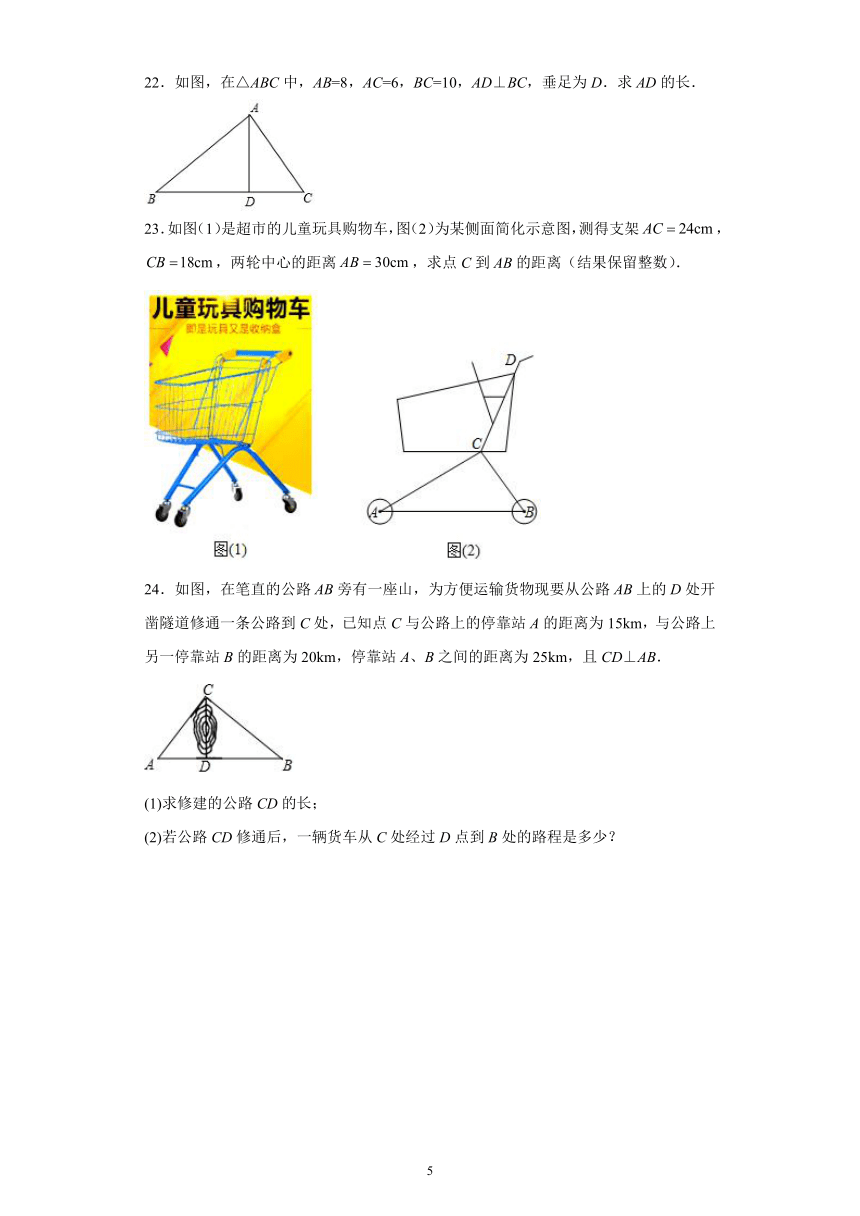
9.如图,中,且,为外一点,连接,过作交于点,为上一点且,连接,.将线段绕点逆时针旋转到线段,连接分别交、于点、,连接、.下列结论:①;②;③;④;⑤若,,,则.其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
10.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若a2=b2+c2,则( )
A.∠A=90° B.∠B=90° C.∠C=90° D.∠C=∠A+∠B
11.三角形三边长分别是6,10,8,则它的最长边上的高为( )
A.6 B.10 C.8 D.4.8
12.小明向东走后,沿方向又走了,再沿方向走了回到原地,则方向是( )
A.南向或北向 B.东向或西向 C.南向 D.北向
13.已知,在中,,,D为BC边上的点,,,则DC的长是( ).
A.6 B.9 C.12 D.15
二、填空题
14.如图,以点为端点的四条射线AB,AC,AD,AE分别过四点,它们依次是,,,,则______(填或“>”、“=”或“<”)
15.已知△ABC中,AB=5, BC=8, BC边上的中线AD=3,则AC=__________________.
16.如图,在的正方形网格中,每个小正方形的顶点称为格点,点、、均在格点上,则______.
17.已知三角形的三边分别是6,8,10,则最长边上的高等于______.
18.如图,点P是等边△ABC内的一点,PA=6,PB=8,PC=10,若点P′是△ABC外的一点,且△P′AB≌△PAC,则∠APB的度数为___.
19.已知一个三角形的三边长分别为cm、3cm、2cm,则这个三角形的面积为_____cm2.
三、解答题
20.省耕文化公园是昭阳区城市的新名片,公园内有一块四边形ABCD草坪.如图所示,∠B=90°,AB=30米,BC=40米,CD=120米,AD=130米,求四边形ABCD草坪的面积.
21.如图,已知等腰△ABC的底边BC=10cm,D是腰AC上一点,且CD=6cm,BD=8cm.
(1)判断△BCD的形状,并说明理由;
(2)求△ABC的周长.
22.如图,在△ABC中,AB=8,AC=6,BC=10,AD⊥BC,垂足为D.求AD的长.
23.如图(1)是超市的儿童玩具购物车,图(2)为某侧面简化示意图,测得支架,,两轮中心的距离,求点C到AB的距离(结果保留整数).
24.如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
试卷第1页,共3页
参考答案:
1.D
解:A、∵12+()2=22,故是直角三角形,不符合题意;
B、32+42=52,故是直角三角形,不符合题意;
C、82+152=172,故是直角三角形,不符合题意;
D、22+32≠42,故不是直角三角形,符合题意;
故选:D.
2.B
解:由题意得:, ,,
∵,
∴,
∴∠BAC=90°,
∴为直角三角形.
故选:B.
3.C
解:设Rt△PMN的边MP=c,MN=b,NP=a,其中c>b>a,
则AB=c,CD=b,EF=a,a2+b2=c2.
∵△EFG,△CDG,△ABG为等腰直角三角形,
∴FG=EG=a,DG=CG=b,BG=AG=c.
∴CF====c,
∵AG=c,
∴CF=AG.
∴A选项正确;
∵AB=c,CD=b,EF=a,
∴CD2+EF2=b2+a2,AB2=c2,
∴CD2+EF2=AB2.
∴以EF,CD,AB为三边的三角形是直角三角形.
∴B选项正确;
∵AE+CG=AC+CE+CG=AG+EC=AG+GC﹣GE=(c+b﹣a),AB=c,
∴AE+CG≠AB.
∴C选项错误;
∵四边形ABDC的面积=S△ABG﹣S△GDC
= BG AG﹣DG GC
=×c×c﹣b×b
= (c2﹣b2)
=,
×FG EG== a2,
∴四边形ABDC的面积与△EFG的面积相等.
∴D选项正确.
综上,结论不成立的是:C.
故选:C.
4.D
解:如图,连接BD,
∵∠A=90°,AB=3cm,AD=4cm,
∴BD==5(cm),
∵BC=13cm,CD=12cm,52+122=132,
∴BD2+CD2=CB2,
∴∠BDC=90°,
∴S△DBC=×DB×CD=×5×12=30(cm2),
S△ABD=×3×4=6(cm2),
∴四边形ABCD的面积为30+6=36(cm2),
故选:D.
5.A
,
不能构成直角三角形,是锐角三角形,
故选:A.
6.B
如图,延长射线AB交格点于点D,
∵每个小正方形的边长为1
∴,
∵
∴∠D=90°
又∵BD=CD
∴△BCD是等腰直角三角形
∴∠DBC=45°
∴∠ABC=180°-∠DBC =180°-45°=135°
故选B.
7.C
解,设每个小方格的长为1
由勾股定理可得,,
∵,即,
∴为等腰直角三角形
∴,
∴
故选C
8.D
解:∵AD=12,BD=5,AB=13,
∴AB2=AD2+BD2,
∴∠ADB=90°,
∵D为BC的中点,BD=CD,
∴AD垂直平分BC,
∴点B,点C关于直线AD对称,
过C作CE⊥AB交AD于P,则此时PE+PB=CE的值最小,
∵S△ABC=AB CE=BC AD,
∴13 CE=10×12,
∴CE=,
∴PE+PB的最小值为,
故选:D.
9.C
解:∵,,
∴,
又∵且,
∴,
∴,,
∴
∵,
∴,
∴,
∴,
∴,
又∵,,
∴,
∴,,故①正确;
∵,
∴,
∴,故②正确;
,即,故④正确;
∵,,,
∴,
∴,故③错误;
如图,连接,
若,,,
∴,
∴,即,
∴,
∴,
∴,故⑤正确;
故选:C.
.
10.A
∵a2=b2+c2
∴∠A=90°
故选A.
11.D
解:∵三角形三边长分别是6,10,8
∴62+82=102
∴该三角形为直角三角形
∴该三角形的面积:6×8÷2=24
斜边上的高:24×2÷10=4.8
∴这个三角形最长边上的高是4.8.
故选:D.
12.A
解:设小明一开始的位置为O,向东走到的位置为C,沿A方向走到的位置为D,
∴由题意得OC=80m,CD=60m,OD=100m,
∴,
∴∠OCD=90°,
∵OC的方向为东,
∴CD的方向为南或北,即A的方向为南或北,
故选A.
13.B
解:如图所示:
∵AB=13,AD=12,BD=5,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴∠ADC=180°﹣∠ADB=90°,
在Rt△ADC中,由勾股定理得:DC9,
故选:B.
14.=
解:连接BC,
∵B(1,2),C(2,4),D(5,3),E(5,1),
∴AE=DE=2,
∴△ADE是等腰直角三角形,
∴∠DAE=45°,
又∵AB=,
同理可得BC=,
AC=,
则在△ABC中,有AB2+BC2=AC2,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
∴∠BAC=∠DAE,
故答案为:=.
15.
解:如图,BC=8, BC边上的中线AD=3,
故答案为:5
16.45°
解:取正方形网格中格点Q,连接PQ和BQ,如下图所示:
∴AE=PF,PE=QF,∠AEP=∠PFQ=90°,
∴△APE≌△PQF(SAS),
∴∠PAB=∠QPF,
∵PF∥BE,
∴∠PBA=∠BPF,
∴∠PAB+∠PBA=∠QPF+∠BPF=∠QPB,
又QA =2 +4 =20,QB =2 +1 =5,AB =5 =25,
∴QA +QB =20+5=25=AB ,
∴△QAB为直角三角形,∠AQB=90°,
∵PQ =2 +1 =5=QB ,
∴△PQB为等腰直角三角形,
∴∠QPB=∠QBP=(180°-90°)÷2=45°,
∴∠PAB+∠PBA=∠QPF+∠BPF=∠QPB=45°,
故答案为:45°.
17./4.8
∵三角形的三边分别是6,8,10,
又∵
∴这个三角形是直角三角形
∵最长边上的高
∴最长边上的高为:
故答案为:.
18.150°
解:连接PP′,
∵△PAC≌△P′AB,
∴PA=P′A,∠P′AB=∠PAC,
∴∠P′AP=∠BAC=60°,
∴△APP′为等边三角形,
∴PP′=AP=AP′=6;
∵PP′2+BP2=BP′2,
∴△BPP′为直角三角形,且∠BPP′=90°,
∴∠APB=90°+60°=150°.
故答案为:150°.
19.
解:∵三角形的三边长分别为cm、3cm、2cm,
∴()2+22=32,
∴这个三角形是直角三角形,斜边长为3cm,
∴这个三角形的面积为2×=(cm2),
故答案为:.
20.3600米2
解:连接AC,如图所示:
在Rt△ABC中,AC2=AB2+BC2=302+402=2500,
∵AC>0,
∴AC=50,
在△CAD中,AC2+CD2=2500+14400=16900=AD2,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴S四边形ABCD=S△BAC+S△ADCAB BCAC DC,
30×4050×120
=3600(米2),
答:这块四边形草坪ABCD的面积是3600米2.
21.(1)△BDC为直角三角形,理由见解析;
(2)△ABC的周长为=cm.
(1)
解:△BDC为直角三角形,理由如下,
∵BC=10cm,CD=8cm,BD=6cm,
而102=62+82,
∴BC2=BD2+CD2.
∴△BDC为直角三角形;
(2)
解:设AB=xcm,
∵等腰△ABC,
∴AB=AC=x,则AD=x-6,
∵AB2=AD2+BD2,
即x2=(x-6)2+82,
∴x=,
∴△ABC的周长=2AB+BC=(cm).
22.4.8
解:在中,
,,,
,
,
,
,
.
23.点到的距离约为
解:过点作于点,则的长即点到的距离,
在中,
,,,
,,
,
为直角三角形,即,
,
,即,
,
答:点到的距离约为.
24.(1)修建的公路CD的长是12km;
(2)一辆货车从C处经过D点到B处的路程是28km.
(1)
解:∵AC=15km,BC=20km,AB=25km,
152+202=252,
∴△ACB是直角三角形,∠ACB=90°,
∵AC×BC=AB×CD,
∴CD=AC×BC÷AB=12(km).
故修建的公路CD的长是12km;
(2)
解:在Rt△BDC中,BD= =16(km),
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28(km).
故一辆货车从C处经过D点到B处的路程是28km.
答案第1页,共2页
一、单选题
1.下列各组数中,不能作为直角三角形的三边长的是( )
A.1,2, B.5,4,3 C.17,8,15 D.2,3,4
2.如图,在 4×4 的正方形网格中(每个小正方形边长均为 1),点A,B,C 在格点上,连接 AB,AC,BC,则△ABC 的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.如图①,分别以Rt△PMN(MN>NP)的三边为斜边向外作三个等腰直角三角形,再按图②的方式将两个较小的等腰直角三角形放在最大的等腰直角三角形内,则下列结论不成立的是( )
A.CF=AG
B.以EF,CD,AB为三边的三角形是直角三角形
C.AE+CG=AB
D.四边形ABDC的面积与△EFG的面积相等
4.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2 B.18cm2 C.22cm2 D.36cm2
5.若一个三角形的三边长分别为3,4,4.5,则这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
6.如图,在每个小正方形的边长为1的网格中,△ABC的的顶点都在格点上.则∠ABC的度数为( )
A.120° B.135° C.150° D.165°
7.在如图的方格中, ABC的顶点 A、 B、 C都是方格线的交点,则三角形 ABC的外角ACD的度数等于( )
A.130 B.140 C.135 D.145
8.已知在等腰三角形ABC中,D为BC的中点AD=12,BD=5,AB=13,点P为AD边上的动点,点E为AB边上的动点,则PE+PB的最小值是( )
A.10 B.12 C. D.
9.如图,中,且,为外一点,连接,过作交于点,为上一点且,连接,.将线段绕点逆时针旋转到线段,连接分别交、于点、,连接、.下列结论:①;②;③;④;⑤若,,,则.其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
10.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若a2=b2+c2,则( )
A.∠A=90° B.∠B=90° C.∠C=90° D.∠C=∠A+∠B
11.三角形三边长分别是6,10,8,则它的最长边上的高为( )
A.6 B.10 C.8 D.4.8
12.小明向东走后,沿方向又走了,再沿方向走了回到原地,则方向是( )
A.南向或北向 B.东向或西向 C.南向 D.北向
13.已知,在中,,,D为BC边上的点,,,则DC的长是( ).
A.6 B.9 C.12 D.15
二、填空题
14.如图,以点为端点的四条射线AB,AC,AD,AE分别过四点,它们依次是,,,,则______(填或“>”、“=”或“<”)
15.已知△ABC中,AB=5, BC=8, BC边上的中线AD=3,则AC=__________________.
16.如图,在的正方形网格中,每个小正方形的顶点称为格点,点、、均在格点上,则______.
17.已知三角形的三边分别是6,8,10,则最长边上的高等于______.
18.如图,点P是等边△ABC内的一点,PA=6,PB=8,PC=10,若点P′是△ABC外的一点,且△P′AB≌△PAC,则∠APB的度数为___.
19.已知一个三角形的三边长分别为cm、3cm、2cm,则这个三角形的面积为_____cm2.
三、解答题
20.省耕文化公园是昭阳区城市的新名片,公园内有一块四边形ABCD草坪.如图所示,∠B=90°,AB=30米,BC=40米,CD=120米,AD=130米,求四边形ABCD草坪的面积.
21.如图,已知等腰△ABC的底边BC=10cm,D是腰AC上一点,且CD=6cm,BD=8cm.
(1)判断△BCD的形状,并说明理由;
(2)求△ABC的周长.
22.如图,在△ABC中,AB=8,AC=6,BC=10,AD⊥BC,垂足为D.求AD的长.
23.如图(1)是超市的儿童玩具购物车,图(2)为某侧面简化示意图,测得支架,,两轮中心的距离,求点C到AB的距离(结果保留整数).
24.如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
试卷第1页,共3页
参考答案:
1.D
解:A、∵12+()2=22,故是直角三角形,不符合题意;
B、32+42=52,故是直角三角形,不符合题意;
C、82+152=172,故是直角三角形,不符合题意;
D、22+32≠42,故不是直角三角形,符合题意;
故选:D.
2.B
解:由题意得:, ,,
∵,
∴,
∴∠BAC=90°,
∴为直角三角形.
故选:B.
3.C
解:设Rt△PMN的边MP=c,MN=b,NP=a,其中c>b>a,
则AB=c,CD=b,EF=a,a2+b2=c2.
∵△EFG,△CDG,△ABG为等腰直角三角形,
∴FG=EG=a,DG=CG=b,BG=AG=c.
∴CF====c,
∵AG=c,
∴CF=AG.
∴A选项正确;
∵AB=c,CD=b,EF=a,
∴CD2+EF2=b2+a2,AB2=c2,
∴CD2+EF2=AB2.
∴以EF,CD,AB为三边的三角形是直角三角形.
∴B选项正确;
∵AE+CG=AC+CE+CG=AG+EC=AG+GC﹣GE=(c+b﹣a),AB=c,
∴AE+CG≠AB.
∴C选项错误;
∵四边形ABDC的面积=S△ABG﹣S△GDC
= BG AG﹣DG GC
=×c×c﹣b×b
= (c2﹣b2)
=,
×FG EG== a2,
∴四边形ABDC的面积与△EFG的面积相等.
∴D选项正确.
综上,结论不成立的是:C.
故选:C.
4.D
解:如图,连接BD,
∵∠A=90°,AB=3cm,AD=4cm,
∴BD==5(cm),
∵BC=13cm,CD=12cm,52+122=132,
∴BD2+CD2=CB2,
∴∠BDC=90°,
∴S△DBC=×DB×CD=×5×12=30(cm2),
S△ABD=×3×4=6(cm2),
∴四边形ABCD的面积为30+6=36(cm2),
故选:D.
5.A
,
不能构成直角三角形,是锐角三角形,
故选:A.
6.B
如图,延长射线AB交格点于点D,
∵每个小正方形的边长为1
∴,
∵
∴∠D=90°
又∵BD=CD
∴△BCD是等腰直角三角形
∴∠DBC=45°
∴∠ABC=180°-∠DBC =180°-45°=135°
故选B.
7.C
解,设每个小方格的长为1
由勾股定理可得,,
∵,即,
∴为等腰直角三角形
∴,
∴
故选C
8.D
解:∵AD=12,BD=5,AB=13,
∴AB2=AD2+BD2,
∴∠ADB=90°,
∵D为BC的中点,BD=CD,
∴AD垂直平分BC,
∴点B,点C关于直线AD对称,
过C作CE⊥AB交AD于P,则此时PE+PB=CE的值最小,
∵S△ABC=AB CE=BC AD,
∴13 CE=10×12,
∴CE=,
∴PE+PB的最小值为,
故选:D.
9.C
解:∵,,
∴,
又∵且,
∴,
∴,,
∴
∵,
∴,
∴,
∴,
∴,
又∵,,
∴,
∴,,故①正确;
∵,
∴,
∴,故②正确;
,即,故④正确;
∵,,,
∴,
∴,故③错误;
如图,连接,
若,,,
∴,
∴,即,
∴,
∴,
∴,故⑤正确;
故选:C.
.
10.A
∵a2=b2+c2
∴∠A=90°
故选A.
11.D
解:∵三角形三边长分别是6,10,8
∴62+82=102
∴该三角形为直角三角形
∴该三角形的面积:6×8÷2=24
斜边上的高:24×2÷10=4.8
∴这个三角形最长边上的高是4.8.
故选:D.
12.A
解:设小明一开始的位置为O,向东走到的位置为C,沿A方向走到的位置为D,
∴由题意得OC=80m,CD=60m,OD=100m,
∴,
∴∠OCD=90°,
∵OC的方向为东,
∴CD的方向为南或北,即A的方向为南或北,
故选A.
13.B
解:如图所示:
∵AB=13,AD=12,BD=5,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴∠ADC=180°﹣∠ADB=90°,
在Rt△ADC中,由勾股定理得:DC9,
故选:B.
14.=
解:连接BC,
∵B(1,2),C(2,4),D(5,3),E(5,1),
∴AE=DE=2,
∴△ADE是等腰直角三角形,
∴∠DAE=45°,
又∵AB=,
同理可得BC=,
AC=,
则在△ABC中,有AB2+BC2=AC2,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
∴∠BAC=∠DAE,
故答案为:=.
15.
解:如图,BC=8, BC边上的中线AD=3,
故答案为:5
16.45°
解:取正方形网格中格点Q,连接PQ和BQ,如下图所示:
∴AE=PF,PE=QF,∠AEP=∠PFQ=90°,
∴△APE≌△PQF(SAS),
∴∠PAB=∠QPF,
∵PF∥BE,
∴∠PBA=∠BPF,
∴∠PAB+∠PBA=∠QPF+∠BPF=∠QPB,
又QA =2 +4 =20,QB =2 +1 =5,AB =5 =25,
∴QA +QB =20+5=25=AB ,
∴△QAB为直角三角形,∠AQB=90°,
∵PQ =2 +1 =5=QB ,
∴△PQB为等腰直角三角形,
∴∠QPB=∠QBP=(180°-90°)÷2=45°,
∴∠PAB+∠PBA=∠QPF+∠BPF=∠QPB=45°,
故答案为:45°.
17./4.8
∵三角形的三边分别是6,8,10,
又∵
∴这个三角形是直角三角形
∵最长边上的高
∴最长边上的高为:
故答案为:.
18.150°
解:连接PP′,
∵△PAC≌△P′AB,
∴PA=P′A,∠P′AB=∠PAC,
∴∠P′AP=∠BAC=60°,
∴△APP′为等边三角形,
∴PP′=AP=AP′=6;
∵PP′2+BP2=BP′2,
∴△BPP′为直角三角形,且∠BPP′=90°,
∴∠APB=90°+60°=150°.
故答案为:150°.
19.
解:∵三角形的三边长分别为cm、3cm、2cm,
∴()2+22=32,
∴这个三角形是直角三角形,斜边长为3cm,
∴这个三角形的面积为2×=(cm2),
故答案为:.
20.3600米2
解:连接AC,如图所示:
在Rt△ABC中,AC2=AB2+BC2=302+402=2500,
∵AC>0,
∴AC=50,
在△CAD中,AC2+CD2=2500+14400=16900=AD2,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴S四边形ABCD=S△BAC+S△ADCAB BCAC DC,
30×4050×120
=3600(米2),
答:这块四边形草坪ABCD的面积是3600米2.
21.(1)△BDC为直角三角形,理由见解析;
(2)△ABC的周长为=cm.
(1)
解:△BDC为直角三角形,理由如下,
∵BC=10cm,CD=8cm,BD=6cm,
而102=62+82,
∴BC2=BD2+CD2.
∴△BDC为直角三角形;
(2)
解:设AB=xcm,
∵等腰△ABC,
∴AB=AC=x,则AD=x-6,
∵AB2=AD2+BD2,
即x2=(x-6)2+82,
∴x=,
∴△ABC的周长=2AB+BC=(cm).
22.4.8
解:在中,
,,,
,
,
,
,
.
23.点到的距离约为
解:过点作于点,则的长即点到的距离,
在中,
,,,
,,
,
为直角三角形,即,
,
,即,
,
答:点到的距离约为.
24.(1)修建的公路CD的长是12km;
(2)一辆货车从C处经过D点到B处的路程是28km.
(1)
解:∵AC=15km,BC=20km,AB=25km,
152+202=252,
∴△ACB是直角三角形,∠ACB=90°,
∵AC×BC=AB×CD,
∴CD=AC×BC÷AB=12(km).
故修建的公路CD的长是12km;
(2)
解:在Rt△BDC中,BD= =16(km),
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28(km).
故一辆货车从C处经过D点到B处的路程是28km.
答案第1页,共2页
