19.3 平行线分三角形两边成比例(一)
文档属性
| 名称 | 19.3 平行线分三角形两边成比例(一) |

|
|
| 格式 | zip | ||
| 文件大小 | 35.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-10 15:04:17 | ||
图片预览

文档简介
19.3 平行线分三角形两边成比例(一)
教学目标
掌握平行线分三角形两边成比例定理(A字形)
结合图形,能对定理中“对应”线段准确的认识
通过应用定理,提高识图能力和逻辑推理能力
教学重点
平行线分三角形两边成比例
教学难点
准确找出对应线段
教学内容
复习
填空:在△ABC中
∵D是AB中点 DE∥BC
∴______=______
∴=______=______
=______=______
叙述定理
经过三角形一边中点且与另一边平行和直线必分第三边
新课
通过刚才的复习我们知道:,
思考:如果把DE平行向上移动,使,那么呢?
如果把DE平行向上移动,使,那么呢?
利用几何画板探究上述结论
思考:如果DE平行移动,使(m、n没有公因数),那么呢?
(利用几何画板进行探究)
得出结论,若DE∥BC,总有()
利用比例的性质,还可以得到:①()
②()
③()
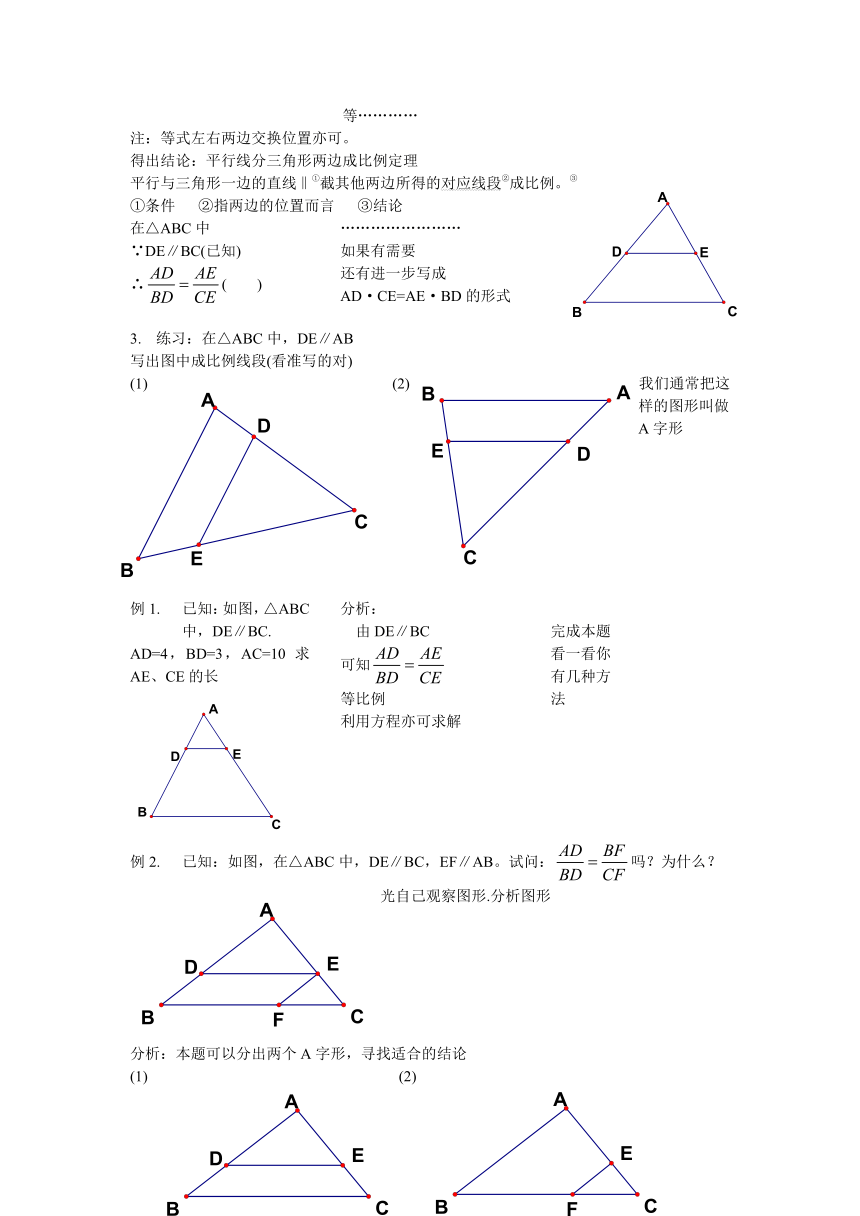
等…………
注:等式左右两边交换位置亦可。
得出结论:平行线分三角形两边成比例定理
平行与三角形一边的直线‖①截其他两边所得的对应线段②成比例。③
①条件 ②指两边的位置而言 ③结论
在△ABC中
∵DE∥BC(已知)
∴( )
……………………
如果有需要
还有进一步写成
AD·CE=AE·BD的形式
练习:在△ABC中,DE∥AB
写出图中成比例线段(看准写的对)
(1) (2) 我们通常把这样的图形叫做A字形
已知:如图,△ABC中,DE∥BC.
AD=4,BD=3,AC=10 求AE、CE的长
分析:
由DE∥BC
可知
等比例
利用方程亦可求解
完成本题
看一看你
有几种方
法
已知:如图,在△ABC中,DE∥BC,EF∥AB。试问:吗?为什么?
光自己观察图形.分析图形
分析:本题可以分出两个A字形,寻找适合的结论
(2)
观察=? 观察=?
解:在△ABC中
∵DE∥BC
∴
∵EF∥AB
∴
∴
分解图形,寻找中间比是本体的关键。
分别看比例式的两边等于什么
练习:已知:如图,EF∥BC,DF∥CE
求证:AE2=AD·AB
检测内容已知:如图,点D、E、F分别在OA、OB、OC上DE∥AB,EF∥BC
求证:
板书设计
平行线分三角形两边成比例
1.平行线分三角形两边成比例定理 例1:
_____________________________ _________________
_____________________________ ________________
_____________________________ _________________
图形变式 例2:
_____________________________ ________________
_____________________________ ________________
_____________________________ _______________
课后反思
小结:1.平行线分三角形两边成比例定理
2.解题方法
教学目标
掌握平行线分三角形两边成比例定理(A字形)
结合图形,能对定理中“对应”线段准确的认识
通过应用定理,提高识图能力和逻辑推理能力
教学重点
平行线分三角形两边成比例
教学难点
准确找出对应线段
教学内容
复习
填空:在△ABC中
∵D是AB中点 DE∥BC
∴______=______
∴=______=______
=______=______
叙述定理
经过三角形一边中点且与另一边平行和直线必分第三边
新课
通过刚才的复习我们知道:,
思考:如果把DE平行向上移动,使,那么呢?
如果把DE平行向上移动,使,那么呢?
利用几何画板探究上述结论
思考:如果DE平行移动,使(m、n没有公因数),那么呢?
(利用几何画板进行探究)
得出结论,若DE∥BC,总有()
利用比例的性质,还可以得到:①()
②()
③()
等…………
注:等式左右两边交换位置亦可。
得出结论:平行线分三角形两边成比例定理
平行与三角形一边的直线‖①截其他两边所得的对应线段②成比例。③
①条件 ②指两边的位置而言 ③结论
在△ABC中
∵DE∥BC(已知)
∴( )
……………………
如果有需要
还有进一步写成
AD·CE=AE·BD的形式
练习:在△ABC中,DE∥AB
写出图中成比例线段(看准写的对)
(1) (2) 我们通常把这样的图形叫做A字形
已知:如图,△ABC中,DE∥BC.
AD=4,BD=3,AC=10 求AE、CE的长
分析:
由DE∥BC
可知
等比例
利用方程亦可求解
完成本题
看一看你
有几种方
法
已知:如图,在△ABC中,DE∥BC,EF∥AB。试问:吗?为什么?
光自己观察图形.分析图形
分析:本题可以分出两个A字形,寻找适合的结论
(2)
观察=? 观察=?
解:在△ABC中
∵DE∥BC
∴
∵EF∥AB
∴
∴
分解图形,寻找中间比是本体的关键。
分别看比例式的两边等于什么
练习:已知:如图,EF∥BC,DF∥CE
求证:AE2=AD·AB
检测内容已知:如图,点D、E、F分别在OA、OB、OC上DE∥AB,EF∥BC
求证:
板书设计
平行线分三角形两边成比例
1.平行线分三角形两边成比例定理 例1:
_____________________________ _________________
_____________________________ ________________
_____________________________ _________________
图形变式 例2:
_____________________________ ________________
_____________________________ ________________
_____________________________ _______________
课后反思
小结:1.平行线分三角形两边成比例定理
2.解题方法
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
