2021-2022学年八年级数学下册(沪科版)第18章 勾股定理单元测试(夯实基础培优卷)(word版 含解析)
文档属性
| 名称 | 2021-2022学年八年级数学下册(沪科版)第18章 勾股定理单元测试(夯实基础培优卷)(word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 999.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览




文档简介
第18章 勾股定理(夯实基础培优卷)
(考试时间:90分钟 试卷满分:100分)
学校:___________姓名:___________班级:___________考号:___________
本卷题型精选核心重难易错典题,具备举一反三之效,覆盖面积广,可充分考查学生双基综合能力!
单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2021·全国·八年级期末)A、B、C表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点 B.BC中点 C.AC中点 D.∠C的平分线与AB的交点
2.(2021·全国·八年级单元测试)如图,在△ABC中,∠C=90°,M是AB的中点,点N在AC上,MN⊥AB,若AC=8,BC=4,则NC的长为( )
A.5 B.4 C.3 D.2
3.(2022·全国·八年级单元测试)若△ABC的三边a,b,c,满足,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
4.(2022·河南·郑州市第八中学八年级期中)在中,,,的对边分别是a,b,c,且,则( )
A. B. C. D.不确定哪个角是直角
5.(2021·四川东坡·八年级期中)如图,有一个长、宽、高分別为、、的长方体,现一只蚂蚁沿长方体表面从A点爬到B点,那么最短的路径是( )
A.3 B. C. D.
6.(2022·福建鲤城·八年级期末)某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M在正视图(主视图)上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
A. B. C.3 D.2
7.(2022·湖南新邵·八年级期末)已知在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则下列结论:①点P在的角平分线上;②直线可以把分成面积相等的两部分;③;④点P是的重心.正确的有( )
A.1个 B.2个 C.3个 D.4个
8.(2022·安徽·八年级单元测试)古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
9.(2022·广东深圳·八年级期末)如图,在三角形,,,是上中点,是射线上一点.是上一点,连接,,,点在上,连接,,,,则的长为( )
A. B.8 C. D.9
10.(2022·浙江嘉兴·八年级期末)如图,在等腰中,,点P是内一点,且,,,以为直角边,点C为直角顶点,作等腰,下列结论:①点A与点D的距离为;②;③;④,其中正确结论有是( )
A.①②③ B.②④ C.①② D.②③④
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·全国·八年级单元测试)在△ABC中,AB=c,AC=b,BC=a,当a、b、c满足_______时,∠B=90°.
12.(2021·天津市实验中学滨海学校八年级期中)在Rt△ABC中,斜边AB=5,直角边BC=3,则△ABC斜边上的高是________
13.(2022·山东莱芜·七年级期末)有一个三角形的两边长是1和,要使这个三角形成为直角三角形,则第三边边长的平方是______.
14.(2022·全国·八年级单元测试)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为 ___.
15.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,平面直角坐标系内有一点A(2,-2),点O是原点,点P是x轴上一动点,如果以P、O、A为顶点的三角形是等腰三角形,那么点P的坐标为_______.
16.(2022·全国·八年级单元测试)如图,每个小正方形的边长都相等,,,是小正方形的顶点,则的度数为______.
17.(2021·四川内江·八年级期末)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC A沿CE翻折,使点A落在AB上的点D处;再将边 BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点 E、F,则△B'FC 的面积为______________.
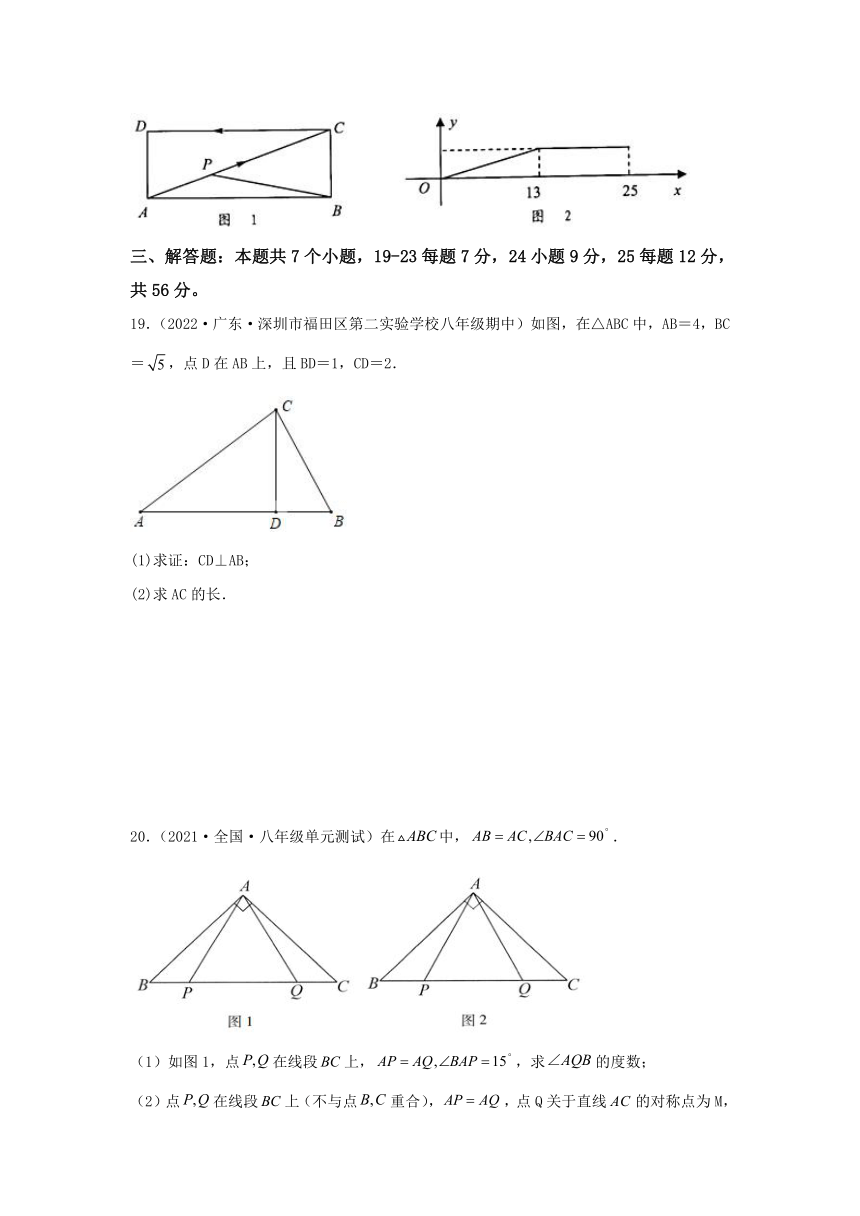
18.(2022·广东龙华·八年级期末)如图1,动点P从长方形ABCD的顶点A出发,沿A→C→D以1cm/s的速度运动到点D停止.设点P的运动时间为x(s),△PAB的面积为y(cm2).表示y与x的函数关系的图象如图2所示,则长方形ABCD的面积为 _____cm2.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,在△ABC中,AB=4,BC=,点D在AB上,且BD=1,CD=2.
(1)求证:CD⊥AB;
(2)求AC的长.
20.(2021·全国·八年级单元测试)在中,.
(1)如图1,点在线段上,,求的度数;
(2)点在线段上(不与点重合),,点Q关于直线的对称点为M,连接.
①依题意将图2补全;
②用等式表示线段之间的数量关系,并证明.
21.(2022·广东·深圳市西乡中学八年级期中)在长方形ABCD中,截取如图所示的阴影部分,已知EC=5,CF=5,FG=4,EG=3,∠EGF=90°.
(1)连接EF,求证:∠FEC=90°;
(2)求出图中阴影部分的面积.
22.(2021·陕西·交大附中分校七年级期末)某运动公园有一块空地,如图,△ABC所示,∠ACB=90°,公园管理处计划在△ADC区域内安装健身器材,其余部分种植草坪,绿化环境.经测量:CD=30米,AD=40米,BC=120米,AB=130米.
(1)求证:∠ADC=90°;
(2)若种植草坪的费用每平方米300元,求种植草坪的总费用.
23.(2021·江苏靖江·八年级期末)如图,某公园有两个小喷泉A、B,两个小喷泉之间的距离为25m.现要为喷泉铺设供水管道AM、BM,供水点M在小路AC上,供水点M到AB的距离MN的长为12m,BM的长为15m.
(1)求供水点M到喷泉A、B需要铺设的管道总长;
(2)试判断BM是否是喷泉B到小路AC的最短距离,若是,请说明理由;若不是,请求出最短距离.
24.(2021·全国·八年级单元测试)在四边形中,,为边上的点.
(1)连接,,;
①如图,若,求证:;
②如图,若,求证:平分;
(2)如图,是的平分线上的点,连接,,若,,,求的长.
25.(2022·湖北汉阳·八年级期末)已知中,如果过项点的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为的关于点的二分割线.例如:如图1,中,,,若过顶点的一条直线交于点,若,显然直线是的关于点的二分割线.
(1)在图2的中,,.请在图2中画出关于点的二分割线,且角度是 ;
(2)已知,在图3中画出不同于图1,图2的,所画同时满足:①为最小角;②存在关于点的二分割线.的度数是 ;
(3)已知,同时满足:①为最小角;②存在关于点的二分割线.请求出的度数(用表示).
第18章 勾股定理(夯实基础培优卷)
(考试时间:90分钟 试卷满分:100分)
学校:___________姓名:___________班级:___________考号:___________
本卷试题共三大题,共25小题,单选10题,填空8题,解答7题,限时90分钟,满分100分,本卷题型精选核心常考重难易错典题,具备举一反三之效,覆盖面积广,可充分考查学生双基综合能力!
单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2021·全国·八年级期末)A、B、C表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点 B.BC中点 C.AC中点 D.∠C的平分线与AB的交点
【答案】A
【分析】根据A、B、C这三个村庄到活动中心P的距离相等,可得点P是 三边垂直平分线的交点,再由勾股定理逆定理,即可求解.
【详解】解:A、B、C这三个村庄到活动中心P的距离相等,
所以点P是 三边垂直平分线的交点,
因为AB=1000米,BC=600米,AC=800米,
所以 ,
所以 是以AB为斜边的直角三角形,
则活动中心P的位置应在斜边AB的中点,
故答案为:A
【点睛】本题主要考查了线段垂直平分线的逆定理,勾股定理的逆定理,熟练掌握线段垂直平分线的逆定理,勾股定理的逆定理是解题的关键.
2.(2021·全国·八年级单元测试)如图,在△ABC中,∠C=90°,M是AB的中点,点N在AC上,MN⊥AB,若AC=8,BC=4,则NC的长为( )
A.5 B.4 C.3 D.2
【答案】C
【分析】连接BN,由中垂线的性质可得AN=BN,设NC=x,则AN=BN=AC-NC=8-x,由勾股定理可得即由此求解即可.
【详解】解:如图所示,连接BN,
∵M为AB的中点,MN⊥AB,
∴AN=BN,
设NC=x,则AN=BN=AC-NC=8-x,
∵∠C=90°,
∴,
∴,
解得,
∴NC=3,
故选C.
【点睛】本题主要考查了勾股定理,中垂线的性质,解题的关键在于能够熟练掌握相关知识进行求解.
3.(2022·全国·八年级单元测试)若△ABC的三边a,b,c,满足,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
【答案】C
【分析】根据非负数的性质可得关于a、b、c的等式,继而可得a、b、c三边的数量关系,进而可判断出△ABC的形状.
【详解】解:∵,
∴a-b=0且a2+b2-c2=0,
∴a=b且a2+b2=c2,
∴△ABC是等腰直角三角形,
故选C.
【点睛】本题考查了等腰直角三角形的判定以及非负数的性质,熟练掌握非负数的性质以及勾股定理的逆定理等知识是解题的关键.
4.(2022·河南·郑州市第八中学八年级期中)在中,,,的对边分别是a,b,c,且,则( )
A. B. C. D.不确定哪个角是直角
【答案】A
【分析】根据题意直接利用勾股定理的逆定理进行判断即可得出答案.
【详解】解:∵在中,,,的对边分别是a,b,c,且,
∴.
∴b、c是两直角边,a是斜边,
∴.
故选:A.
【点睛】本题考查勾股定理的逆定理.注意掌握如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形.
5.(2021·四川东坡·八年级期中)如图,有一个长、宽、高分別为、、的长方体,现一只蚂蚁沿长方体表面从A点爬到B点,那么最短的路径是( )
A.3 B. C. D.
【答案】A
【分析】将图形分三种情况展开,利用勾股定理求出两种情况下斜边的长进行比较,其值最小者即为正确答案..
【详解】解:如图(1),AB=(m);
如图(2),AB=2(m);
如图(3),AB=3(m),
∵,
∴最短的路径是3m.
故选:A.
【点睛】本题主要考查了勾股定理的应用,两点之间线段最短,解题的关键在于能够把长方体展开,利用勾股定理求解.
6.(2022·福建鲤城·八年级期末)某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M在正视图(主视图)上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
A. B. C.3 D.2
【答案】B
【分析】首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,点M在上底面上,点N在下底面上,并且将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果.
【详解】解:根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的为长的长方形的对角线的端点处,如图,
所以所求的最短路径的长度为.
故选:B.
【点睛】本题考查了由三视图判断几何体,平面展开-最短路径问题,简单组合体的三视图,关键是得到点M、N所在位置.
7.(2022·湖南新邵·八年级期末)已知在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则下列结论:①点P在的角平分线上;②直线可以把分成面积相等的两部分;③;④点P是的重心.正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】连接AP并延长交BC于E,连接BP并延长交AC于F,连接CM并延长交AB于M.根据三角形的重心的概念可得P为△ABC的重心,可判断②④正确;利用勾股定理求出AC=BC=2,利用等腰三角形的性质可判断①③正确.
【详解】解:如图,连接AP并延长交BC于E,连接BP并延长交AC于F,连接CM并延长交AB于M.
∵点E、F分别是BC、AC的中点,
∴AE、BF是△ABC的中线,
∴点P是△ABC的重心,直线BP可以把△ABC分成面积相等的两部分;故②④正确;
∴CM是△ABC的中线.
由勾股定理得,AC==2,BC==2,
∴AC=BC,
∴∠BAC=∠ABC;故③正确;
∵AC=BC,CM是△ABC的中线,
∴∠ACM=∠BCM,
∴点P在∠ACB的角平分线上;故①正确.
故选:D.
【点睛】本题考查了三角形的重心的概念,三角形的重心是三角形三边中线的交点.也考查了勾股定理,等腰三角形的性质.得出点P是△ABC的重心是解题的关键.
8.(2022·安徽·八年级单元测试)古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
【答案】D
【分析】根据勾股定理逆定理解题.
【详解】解:设相邻两个结点的距离为m,则此三角形三边的长分别为3m、4m、5m,
∵
∴以3m、4m、5m为边长的三角形是直角三角形.(如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形)
故选D.
【点睛】本题考查勾股定理的逆定理.
9.(2022·广东深圳·八年级期末)如图,在三角形,,,是上中点,是射线上一点.是上一点,连接,,,点在上,连接,,,,则的长为( )
A. B.8 C. D.9
【答案】D
【分析】延长EA到K,是的AK=AG,连接CK,先由勾股定理的逆定理可以得到△ABC是等腰直角三角形,∠BAC=90°,∠ACB=∠ABC=45°,由BF=FE,得到∠FBE=∠FEB,设∠BFE=x,则,然后证明CB=FC=FE,得到∠FBC=∠FCA,∠AFB=∠AFC则,即可证明,推出;设,证明△ABG≌△ACK,得到,,即可推出∠ECK=∠K,得到EK=EC,则,由此即可得到答案.
【详解】解:延长EA到K,是的AK=AG,连接CK,
∵在三角形,,,
∴△ABC是等腰直角三角形,∠BAC=90°,
∴∠ACB=∠ABC=45°,
∵BF=FE,
∴∠FBE=∠FEB,
设∠BFE=x,则,
∵H是BC上中点,F是射线AH上一点,
∴AH⊥BC,
∴AH是线段BC的垂直平分线,∠FAC=45°,
∴CB=FC=FE,
∴∠FBC=∠FCA,∠AFB=∠AFC
∴,
∴,
∴,
∴,
∴,
∴,
设,
∵AG=AK,AB=AC,∠KAC=∠GAB=90°,
∴△ABG≌△ACK(SAS),
,,
∴,
∴∠ECK=∠K,
∴EK=EC,
∵,
∴,
∴,
故选D.
【点睛】本题主要考查了勾股定理和勾股定理的逆定理,等腰三角形的性质与判定,线段垂直平分线的性质与判定,全等三角形的性质与判定,三角形内角和定理等等,熟知相关知识是解题的关键.
10.(2022·浙江嘉兴·八年级期末)如图,在等腰中,,点P是内一点,且,,,以为直角边,点C为直角顶点,作等腰,下列结论:①点A与点D的距离为;②;③;④,其中正确结论有是( )
A.①②③ B.②④ C.①② D.②③④
【答案】C
【分析】连结AD,由等腰 ,可得AC=BC,等腰,可得CD=CP,由余角性质可∠DCA=∠PCB,可证△ADC≌△BPC(SAS)可判断①,由勾股定理DP=,再由,可证△ADP为等腰直角三角形,可判断②,由PB与PD可求BD=2,由勾股定理AB=,可判断③,由面积可判断④即可
【详解】解:连结AD,
在等腰中,,
∴AC=BC,
∵是等腰三角形,
∴CD=CP,
∴∠ACD+ACP=90°,∠ACP+∠PCB=90°,
∴∠DCA=∠PCB,
在△ADC和△BPC中,
AC=BC,
∠DCA=∠PCB,
DC=PC,
∴△ADC≌△BPC(SAS),
∴,
①点A与点D的距离为正确,
在Rt△DCP中,由勾股定理DP=,
在△ADP中,,
∴△ADP为等腰直角三角形,
∴AD⊥DP,
②正确;
BD=BP+PD=2,
在Rt△ADB中,由勾股定理,
AB=,
③不正确;
,
④不正确.
故选择:C.
【点睛】本题考查等腰直角三角形的性质与判定,三角形全等的判定与性质,三角形面积,勾股定理的应用,掌握等腰直角三角形的性质与判定,三角形全等的判定与性质,三角形面积,勾股定理的应用是解题关键.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·全国·八年级单元测试)在△ABC中,AB=c,AC=b,BC=a,当a、b、c满足_______时,∠B=90°.
【答案】a2+c2= b2
【分析】根据勾股定理的逆定理可得到满足的条件,可得到答案.
【详解】解:∵a2+c2=b2时,△ABC是以AC为斜边的直角三角形,
∴当a、b、c满足a2+c2=b2时,∠B=90°.
故答案为:a2+c2=b2.
【点睛】本题主要考查勾股定理的逆定理,掌握当两边平方和等于第三边的平方时第三边所对的角为直角是解题的关键.
12.(2021·天津市实验中学滨海学校八年级期中)在Rt△ABC中,斜边AB=5,直角边BC=3,则△ABC斜边上的高是________
【答案】
【分析】根据勾股定理及三角形的面积公式即可解答.
【详解】解:∵在Rt△ABC中,斜边AB=5,直角边BC=3,
∴另一直角边AC为:,
∴△ABC的面积=AB边上的高h=×AC×BC.
∴AB边上的高h=.
故答案为: .
【点睛】本题考查勾股定理,三角形面积,解决本题的关键是利用勾股定理求得另一直角边的长,比较简单.
13.(2022·山东莱芜·七年级期末)有一个三角形的两边长是1和,要使这个三角形成为直角三角形,则第三边边长的平方是______.
【答案】1或3
【分析】分第三边是直角边与斜边两种情况进行讨论,利用勾股定理即可求解.
【详解】解:当第三边是斜边时,第三边边长的平方是:12+()2=3;
当第三边是直角边时,第三边边长的平方是:()212=1;
故答案是:1或3.
【点睛】本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.分两种情况讨论是解题的关键.
14.(2022·全国·八年级单元测试)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为 ___.
【答案】4
【分析】设AQ=DQ=x,则BQ=AB﹣AQ=9﹣x,在Rt△BDQ中,用勾股定理列方程可解得x,从而可得答案.
【详解】解:∵BC=6,D是BC的中点,
∴BD=BC=3,
∵△ABC折叠,使A点与BC的中点D重合,
∴AQ=DQ,
设AQ=DQ=x,则BQ=AB﹣AQ=9﹣x,
在Rt△BDQ中,
∴
解得x=5,
∴BQ=9﹣x=4,
故答案为:4.
【点睛】本题考查折叠的性质和勾股定理,关键是利用方程思想设边长,然后用勾股定理列方程解未知数,求边长.
15.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,平面直角坐标系内有一点A(2,-2),点O是原点,点P是x轴上一动点,如果以P、O、A为顶点的三角形是等腰三角形,那么点P的坐标为_______.
【答案】(,0)或(4,0)或(-2,0)或(2,0)
【分析】根据题意分类讨论,①OA为等腰三角形底边,②OA为等腰三角形一条腰,根据等腰三角形的性质求解即可.
【详解】解:设,
A(2,-2)
如图:①OA为等腰三角形底边,
即
解得
符合条件的动点P有一个,即(2,0);
②OA为等腰三角形一条腰,
当时,
即
解得
当时,
解得或(舍去)
符合符合条件的动点P有三个即(-2,0),(2,0),(4,0).
综上所述,符合条件的点P的坐标是:(,0)或(4,0)或(-2,0)或(2,0).
故答案为:(,0)或(4,0)或(-2,0)或(2,0).
【点睛】此题主要考查了等腰三角形的判定及坐标与图形的性质;利用等腰三角形的判定来解决实际问题,其关键是根据题意,画出符合实际条件的图形,根据等腰三角形的性质求解.
16.(2022·全国·八年级单元测试)如图,每个小正方形的边长都相等,,,是小正方形的顶点,则的度数为______.
【答案】
【分析】连接 ,设小正方形的边长为 ,由勾股定理可得 , ,再由勾股定理逆定理可得 ,即可求解.
【详解】解:如图,连接 ,
设小正方形的边长为 ,由勾股定理得:
,
,
,
∴ , ,
∴ , ,
∴ .
故答案为:.
【点睛】本题主要考查了勾股定理及逆定理,等腰三角形的性质,根据勾股定理得出 、 、 是解题的关键.
17.(2021·四川内江·八年级期末)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC A沿CE翻折,使点A落在AB上的点D处;再将边 BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点 E、F,则△B'FC 的面积为______________.
【答案】
【分析】由题意可得AB=10,根据面积可得CE=4.8,根据勾股定理可求BE=6.4,由折叠可求∠ECF=45°,可得EC=EF=4.8,即可求BF的长,可求面积.
【详解】解:∵Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴BA= =10,
∵将边AC沿CE翻折,使点A落在AB上的点D处,
∴∠AEC=∠CED,∠ACE=∠DCE,
∵∠AED=180°,
∴∠CED=90°,即CE⊥AB,
∵S△ABC= AB×EC=AC×BC,
∴EC=4.8,
在Rt△BCE中,BE==6.4,
∵将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,
∴BF=B'F,∠BCF=∠B'CF,
∵∠BCF+∠B'CF+∠ACE+∠DCE=∠ACB=90°,
∴ECF=45°,
又CE⊥AB,
∴∠EFC=∠ECF=45°,
∴CE=EF=4.8,
∵BF=BE-EF=6.4-4.8=1.6,
∴△BFC的面积为:FB×EC=,
由翻折可知,△B'FC 的面积=△BFC的面积=
故答案为.
【点睛】本题考查了折叠问题,勾股定理,根据折叠的性质求∠ECF=45°是本题的关键.
18.(2022·广东龙华·八年级期末)如图1,动点P从长方形ABCD的顶点A出发,沿A→C→D以1cm/s的速度运动到点D停止.设点P的运动时间为x(s),△PAB的面积为y(cm2).表示y与x的函数关系的图象如图2所示,则长方形ABCD的面积为 _____cm2.
【答案】60
【分析】根据题意可得AC=13cm,CD=25-13=12(cm),根据勾股定理可得AD的值,进而得出长方形ABCD的面积.
【详解】解:由图象,结合题意可得AC=13cm,CD=25-13=12(cm),
∴AD==5(cm),
∴长方形ABCD的面积为:12×5=60(cm2).
故答案为:60.
【点睛】本题考查了动点问题的函数图象,解决本题应首先看清横轴和纵轴表示的量.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,在△ABC中,AB=4,BC=,点D在AB上,且BD=1,CD=2.
(1)求证:CD⊥AB;
(2)求AC的长.
【答案】(1)见解析;(2)
【分析】
(1)根据勾股定理逆定理证明△BCD是直角三角形,即可得证;
(2)先求得AD=,在Rt△ACD中,勾股定理求解即可.
【详解】解:(1)证明:∵在△BCD中,BD=1,CD=2,BC=,
∴BD2+CD2=12+22=()2=BC2,
∴△BCD是直角三角形,且∠CDB=90°,
∴CD⊥AB;
(2)
解:∵CD⊥AB,
∴∠ADC=90°,
∵AB=4,DB=1,
∴AD=3,
在Rt△ACD中,∵CD=2,
∴AC===,
∴AC的长为.
【点睛】本题考查了勾股定理以及勾股定理的逆定理,掌握勾股定理是解题的关键.
20.(2021·全国·八年级单元测试)在中,.
(1)如图1,点在线段上,,求的度数;
(2)点在线段上(不与点重合),,点Q关于直线的对称点为M,连接.
①依题意将图2补全;
②用等式表示线段之间的数量关系,并证明.
【答案】(1);(2)①见解析;②,证明见解析
【分析】
(1)根据三角形的外角性质和等腰三角形的性质可以得解;
(2)①根据轴对称的意义和性质可以作出图形;
②连结MC,然后根据轴对称的性质和直角等腰三角形的性质以及三角形全等的判定和性质可以得到解答.
【详解】解:(1)∵在中,,
.
是的一个外角,
.
,
.
,
.
(2)①如图,由题意可得补全图如下:
②,理由如下:
如上图,连接.
,
.
,
.
.
.
.
∵点Q关于直线的对称点为M,
.
,
∴△ABP≌△ACM,
∴BP=CM,
.
在中,,
.
,
.
在中,,
,
【点睛】本题考查直角三角形的综合应用,熟练掌握直角等腰三角形和三角形的性质、轴对称的意义和性质、三角形全等的判定和性质以及勾股定理的应用是解题关键.
21.(2022·广东·深圳市西乡中学八年级期中)在长方形ABCD中,截取如图所示的阴影部分,已知EC=5,CF=5,FG=4,EG=3,∠EGF=90°.
(1)连接EF,求证:∠FEC=90°;
(2)求出图中阴影部分的面积.
【答案】(1)见解析;(2)
【分析】
(1)先求EF,再利用勾股定理的逆定理得出△EFC为直角三角形,即可得证;
(2)先求出和的面积,再利用得出阴影部分的面积.
【详解】解:(1)∵∠EGF=90°,根据勾股定理得:
EF=,
∵,,
∴,
∴△EFC为直角三角形,
∴∠FEC=90°;
(2)∵,,
∴.
【点睛】本题考查了勾股定理及其逆定理,灵活运用勾股定理是解题的关键.
22.(2021·陕西·交大附中分校七年级期末)某运动公园有一块空地,如图,△ABC所示,∠ACB=90°,公园管理处计划在△ADC区域内安装健身器材,其余部分种植草坪,绿化环境.经测量:CD=30米,AD=40米,BC=120米,AB=130米.
(1)求证:∠ADC=90°;
(2)若种植草坪的费用每平方米300元,求种植草坪的总费用.
【答案】(1)见解析;(2)720000元
【分析】
(1)首先在中利用勾股定理求出AC的长,再利用勾股定理逆定理证明为直角三角形,即可证得;
(2)用S阴影,分别计算出两个直角三角形的面积代入即可.
【详解】解:(1)证明:在中,
∵,
∴,
又∵,
∴,
∴是直角三角形,
∴;
(2)S阴影
(平方米),
总费用:(元)
答:种植草坪的总费用是720000元.
【点睛】本题考查勾股定理及其逆定理的应用,利用勾股定理的逆定理证明直角三角形是解题的关键.
23.(2021·江苏靖江·八年级期末)如图,某公园有两个小喷泉A、B,两个小喷泉之间的距离为25m.现要为喷泉铺设供水管道AM、BM,供水点M在小路AC上,供水点M到AB的距离MN的长为12m,BM的长为15m.
(1)求供水点M到喷泉A、B需要铺设的管道总长;
(2)试判断BM是否是喷泉B到小路AC的最短距离,若是,请说明理由;若不是,请求出最短距离.
【答案】(1)供水点M到喷泉A、B铺设的管道总长为35m;(2)是到小路的最短距离,见解析.
【分析】
(1)在中,利用勾股定理解得的长,继而解得的长,在中,利用勾股定理解得的长,据此解题;
(2)根据勾股定理的逆定理证明是直角三角形,再结合垂线段最短性质解题.
【详解】解:(1)∵
∴
在中,
∴
∴
在中
∴
答:供水点M到喷泉A、B铺设的管道总长为35m.
(2)是到小路的最短距离,
∵,
∴是直角三角形
根据垂线段最短性质,得
是到小路的最短距离.
【点睛】本题考查勾股定理及其逆定理的应用、垂线段最短等知识,是重要考点,难度较易,掌握相关知识是解题关键.
24.(2021·全国·八年级单元测试)在四边形中,,为边上的点.
(1)连接,,;
①如图,若,求证:;
②如图,若,求证:平分;
(2)如图,是的平分线上的点,连接,,若,,,求的长.
【答案】(1)①见解析;②见解析;(2).
【分析】
(1)①根据条件得出,即可求证;
②延长交的延长线于点,得出再证明即可;
(2)解法1:过点分别作,,得到,由,,得到,设,求得,在和中,由勾股定理即可求得的长.
解法2:在上截取,得出,过作,根据,即可求得的长.
【详解】解:(1)①证明:,
,,
,
在和中
,,,
,
.
②证明:延长交的延长线于点,
,
,,
,
,
,
,
,
,
,
,
平分.
(2)解法1:如图,过点分别作,,分别交及的延长线于点,.
平分,
,
又,,
,
在和中
,,,
,
,,
在和中
,,,
,
设,
,,
,,
,
,
,
,
在和中
,,,
.
解法2:如图,在上截取,
,,
,
在和中
,,,
,
,
,
,
过作,垂足为,
,
,
在和中
.
【点睛】本题主要考查了全等三角形的判定和性质,角平分线的判定,以及勾股定理的应用,解题的关键是熟练掌握全等三角形的判定和性质,正确作出辅助线以及利用方程解决问题.
25.(2022·湖北汉阳·八年级期末)已知中,如果过项点的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为的关于点的二分割线.例如:如图1,中,,,若过顶点的一条直线交于点,若,显然直线是的关于点的二分割线.
(1)在图2的中,,.请在图2中画出关于点的二分割线,且角度是 ;
(2)已知,在图3中画出不同于图1,图2的,所画同时满足:①为最小角;②存在关于点的二分割线.的度数是 ;
(3)已知,同时满足:①为最小角;②存在关于点的二分割线.请求出的度数(用表示).
【答案】(1)作图见解析,;(2)作图见解析,;(3)∠A=45°或90°或90°-2α或,或α=45°时45°<∠BAC<90°.
【分析】
(1)根据二分割线的定义,只要把∠ABC分成90°角和20°角即可;
(2)可以画出∠A=35°的三角形;
(3)设BD为△ABC的二分割线,分以下两种情况.第一种情况:△BDC是等腰三角形,△ABD是直角三角形;第二种情况:△BDC是直角三角形,△ABD是等腰三角形分别利用直角三角形的性质、等腰三角形的性质和三角形的内角和定理解答即可.
【详解】解:(1)关于点的二分割线BD如图4所示,;
故答案为:20°;
(2)如图所示:∠BAC=35°;
(3)设BD为△ABC的二分割线,分以下两种情况.
第一种情况:△BDC是等腰三角形,△ABD是直角三角形,易知∠C和∠DBC必为底角,
∴∠DBC=∠C=.
当∠A=90°时,△ABC存在二分分割线;
当∠ABD=90°时,△ABC存在二分分割线,此时∠A=90°-2α;
当∠ADB=90°时,△ABC存在二分割线,此时α=45°且45°<∠A<90°;
第二种情况:△BDC是直角三角形,△ABD是等腰三角形,
当∠DBC=90°时,若BD=AD,则△ABC存在二分割线,此时;
当∠BDC=90°时,若BD=AD,则△ABC存在二分割线,此时∠A=45°,
综上,∠A=45°或90°或90°-2α或,或α=45°时,45°<∠BAC<90°.
【点睛】本题考查的是二分割线的理解与作图,属于新定义题型,主要考查了等腰三角形的性质、直角三角形的性质和三角形的内角和定理等知识,正确理解二分割线的定义、熟练掌握等腰三角形和直角三角形的性质是解答的关键.
(考试时间:90分钟 试卷满分:100分)
学校:___________姓名:___________班级:___________考号:___________
本卷题型精选核心重难易错典题,具备举一反三之效,覆盖面积广,可充分考查学生双基综合能力!
单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2021·全国·八年级期末)A、B、C表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点 B.BC中点 C.AC中点 D.∠C的平分线与AB的交点
2.(2021·全国·八年级单元测试)如图,在△ABC中,∠C=90°,M是AB的中点,点N在AC上,MN⊥AB,若AC=8,BC=4,则NC的长为( )
A.5 B.4 C.3 D.2
3.(2022·全国·八年级单元测试)若△ABC的三边a,b,c,满足,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
4.(2022·河南·郑州市第八中学八年级期中)在中,,,的对边分别是a,b,c,且,则( )
A. B. C. D.不确定哪个角是直角
5.(2021·四川东坡·八年级期中)如图,有一个长、宽、高分別为、、的长方体,现一只蚂蚁沿长方体表面从A点爬到B点,那么最短的路径是( )
A.3 B. C. D.
6.(2022·福建鲤城·八年级期末)某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M在正视图(主视图)上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
A. B. C.3 D.2
7.(2022·湖南新邵·八年级期末)已知在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则下列结论:①点P在的角平分线上;②直线可以把分成面积相等的两部分;③;④点P是的重心.正确的有( )
A.1个 B.2个 C.3个 D.4个
8.(2022·安徽·八年级单元测试)古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
9.(2022·广东深圳·八年级期末)如图,在三角形,,,是上中点,是射线上一点.是上一点,连接,,,点在上,连接,,,,则的长为( )
A. B.8 C. D.9
10.(2022·浙江嘉兴·八年级期末)如图,在等腰中,,点P是内一点,且,,,以为直角边,点C为直角顶点,作等腰,下列结论:①点A与点D的距离为;②;③;④,其中正确结论有是( )
A.①②③ B.②④ C.①② D.②③④
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·全国·八年级单元测试)在△ABC中,AB=c,AC=b,BC=a,当a、b、c满足_______时,∠B=90°.
12.(2021·天津市实验中学滨海学校八年级期中)在Rt△ABC中,斜边AB=5,直角边BC=3,则△ABC斜边上的高是________
13.(2022·山东莱芜·七年级期末)有一个三角形的两边长是1和,要使这个三角形成为直角三角形,则第三边边长的平方是______.
14.(2022·全国·八年级单元测试)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为 ___.
15.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,平面直角坐标系内有一点A(2,-2),点O是原点,点P是x轴上一动点,如果以P、O、A为顶点的三角形是等腰三角形,那么点P的坐标为_______.
16.(2022·全国·八年级单元测试)如图,每个小正方形的边长都相等,,,是小正方形的顶点,则的度数为______.
17.(2021·四川内江·八年级期末)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC A沿CE翻折,使点A落在AB上的点D处;再将边 BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点 E、F,则△B'FC 的面积为______________.
18.(2022·广东龙华·八年级期末)如图1,动点P从长方形ABCD的顶点A出发,沿A→C→D以1cm/s的速度运动到点D停止.设点P的运动时间为x(s),△PAB的面积为y(cm2).表示y与x的函数关系的图象如图2所示,则长方形ABCD的面积为 _____cm2.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,在△ABC中,AB=4,BC=,点D在AB上,且BD=1,CD=2.
(1)求证:CD⊥AB;
(2)求AC的长.
20.(2021·全国·八年级单元测试)在中,.
(1)如图1,点在线段上,,求的度数;
(2)点在线段上(不与点重合),,点Q关于直线的对称点为M,连接.
①依题意将图2补全;
②用等式表示线段之间的数量关系,并证明.
21.(2022·广东·深圳市西乡中学八年级期中)在长方形ABCD中,截取如图所示的阴影部分,已知EC=5,CF=5,FG=4,EG=3,∠EGF=90°.
(1)连接EF,求证:∠FEC=90°;
(2)求出图中阴影部分的面积.
22.(2021·陕西·交大附中分校七年级期末)某运动公园有一块空地,如图,△ABC所示,∠ACB=90°,公园管理处计划在△ADC区域内安装健身器材,其余部分种植草坪,绿化环境.经测量:CD=30米,AD=40米,BC=120米,AB=130米.
(1)求证:∠ADC=90°;
(2)若种植草坪的费用每平方米300元,求种植草坪的总费用.
23.(2021·江苏靖江·八年级期末)如图,某公园有两个小喷泉A、B,两个小喷泉之间的距离为25m.现要为喷泉铺设供水管道AM、BM,供水点M在小路AC上,供水点M到AB的距离MN的长为12m,BM的长为15m.
(1)求供水点M到喷泉A、B需要铺设的管道总长;
(2)试判断BM是否是喷泉B到小路AC的最短距离,若是,请说明理由;若不是,请求出最短距离.
24.(2021·全国·八年级单元测试)在四边形中,,为边上的点.
(1)连接,,;
①如图,若,求证:;
②如图,若,求证:平分;
(2)如图,是的平分线上的点,连接,,若,,,求的长.
25.(2022·湖北汉阳·八年级期末)已知中,如果过项点的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为的关于点的二分割线.例如:如图1,中,,,若过顶点的一条直线交于点,若,显然直线是的关于点的二分割线.
(1)在图2的中,,.请在图2中画出关于点的二分割线,且角度是 ;
(2)已知,在图3中画出不同于图1,图2的,所画同时满足:①为最小角;②存在关于点的二分割线.的度数是 ;
(3)已知,同时满足:①为最小角;②存在关于点的二分割线.请求出的度数(用表示).
第18章 勾股定理(夯实基础培优卷)
(考试时间:90分钟 试卷满分:100分)
学校:___________姓名:___________班级:___________考号:___________
本卷试题共三大题,共25小题,单选10题,填空8题,解答7题,限时90分钟,满分100分,本卷题型精选核心常考重难易错典题,具备举一反三之效,覆盖面积广,可充分考查学生双基综合能力!
单选题:本题共10个小题,每小题2分,共20分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.(2021·全国·八年级期末)A、B、C表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点 B.BC中点 C.AC中点 D.∠C的平分线与AB的交点
【答案】A
【分析】根据A、B、C这三个村庄到活动中心P的距离相等,可得点P是 三边垂直平分线的交点,再由勾股定理逆定理,即可求解.
【详解】解:A、B、C这三个村庄到活动中心P的距离相等,
所以点P是 三边垂直平分线的交点,
因为AB=1000米,BC=600米,AC=800米,
所以 ,
所以 是以AB为斜边的直角三角形,
则活动中心P的位置应在斜边AB的中点,
故答案为:A
【点睛】本题主要考查了线段垂直平分线的逆定理,勾股定理的逆定理,熟练掌握线段垂直平分线的逆定理,勾股定理的逆定理是解题的关键.
2.(2021·全国·八年级单元测试)如图,在△ABC中,∠C=90°,M是AB的中点,点N在AC上,MN⊥AB,若AC=8,BC=4,则NC的长为( )
A.5 B.4 C.3 D.2
【答案】C
【分析】连接BN,由中垂线的性质可得AN=BN,设NC=x,则AN=BN=AC-NC=8-x,由勾股定理可得即由此求解即可.
【详解】解:如图所示,连接BN,
∵M为AB的中点,MN⊥AB,
∴AN=BN,
设NC=x,则AN=BN=AC-NC=8-x,
∵∠C=90°,
∴,
∴,
解得,
∴NC=3,
故选C.
【点睛】本题主要考查了勾股定理,中垂线的性质,解题的关键在于能够熟练掌握相关知识进行求解.
3.(2022·全国·八年级单元测试)若△ABC的三边a,b,c,满足,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
【答案】C
【分析】根据非负数的性质可得关于a、b、c的等式,继而可得a、b、c三边的数量关系,进而可判断出△ABC的形状.
【详解】解:∵,
∴a-b=0且a2+b2-c2=0,
∴a=b且a2+b2=c2,
∴△ABC是等腰直角三角形,
故选C.
【点睛】本题考查了等腰直角三角形的判定以及非负数的性质,熟练掌握非负数的性质以及勾股定理的逆定理等知识是解题的关键.
4.(2022·河南·郑州市第八中学八年级期中)在中,,,的对边分别是a,b,c,且,则( )
A. B. C. D.不确定哪个角是直角
【答案】A
【分析】根据题意直接利用勾股定理的逆定理进行判断即可得出答案.
【详解】解:∵在中,,,的对边分别是a,b,c,且,
∴.
∴b、c是两直角边,a是斜边,
∴.
故选:A.
【点睛】本题考查勾股定理的逆定理.注意掌握如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形.
5.(2021·四川东坡·八年级期中)如图,有一个长、宽、高分別为、、的长方体,现一只蚂蚁沿长方体表面从A点爬到B点,那么最短的路径是( )
A.3 B. C. D.
【答案】A
【分析】将图形分三种情况展开,利用勾股定理求出两种情况下斜边的长进行比较,其值最小者即为正确答案..
【详解】解:如图(1),AB=(m);
如图(2),AB=2(m);
如图(3),AB=3(m),
∵,
∴最短的路径是3m.
故选:A.
【点睛】本题主要考查了勾股定理的应用,两点之间线段最短,解题的关键在于能够把长方体展开,利用勾股定理求解.
6.(2022·福建鲤城·八年级期末)某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M在正视图(主视图)上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
A. B. C.3 D.2
【答案】B
【分析】首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,点M在上底面上,点N在下底面上,并且将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果.
【详解】解:根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的为长的长方形的对角线的端点处,如图,
所以所求的最短路径的长度为.
故选:B.
【点睛】本题考查了由三视图判断几何体,平面展开-最短路径问题,简单组合体的三视图,关键是得到点M、N所在位置.
7.(2022·湖南新邵·八年级期末)已知在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则下列结论:①点P在的角平分线上;②直线可以把分成面积相等的两部分;③;④点P是的重心.正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】连接AP并延长交BC于E,连接BP并延长交AC于F,连接CM并延长交AB于M.根据三角形的重心的概念可得P为△ABC的重心,可判断②④正确;利用勾股定理求出AC=BC=2,利用等腰三角形的性质可判断①③正确.
【详解】解:如图,连接AP并延长交BC于E,连接BP并延长交AC于F,连接CM并延长交AB于M.
∵点E、F分别是BC、AC的中点,
∴AE、BF是△ABC的中线,
∴点P是△ABC的重心,直线BP可以把△ABC分成面积相等的两部分;故②④正确;
∴CM是△ABC的中线.
由勾股定理得,AC==2,BC==2,
∴AC=BC,
∴∠BAC=∠ABC;故③正确;
∵AC=BC,CM是△ABC的中线,
∴∠ACM=∠BCM,
∴点P在∠ACB的角平分线上;故①正确.
故选:D.
【点睛】本题考查了三角形的重心的概念,三角形的重心是三角形三边中线的交点.也考查了勾股定理,等腰三角形的性质.得出点P是△ABC的重心是解题的关键.
8.(2022·安徽·八年级单元测试)古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
【答案】D
【分析】根据勾股定理逆定理解题.
【详解】解:设相邻两个结点的距离为m,则此三角形三边的长分别为3m、4m、5m,
∵
∴以3m、4m、5m为边长的三角形是直角三角形.(如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形)
故选D.
【点睛】本题考查勾股定理的逆定理.
9.(2022·广东深圳·八年级期末)如图,在三角形,,,是上中点,是射线上一点.是上一点,连接,,,点在上,连接,,,,则的长为( )
A. B.8 C. D.9
【答案】D
【分析】延长EA到K,是的AK=AG,连接CK,先由勾股定理的逆定理可以得到△ABC是等腰直角三角形,∠BAC=90°,∠ACB=∠ABC=45°,由BF=FE,得到∠FBE=∠FEB,设∠BFE=x,则,然后证明CB=FC=FE,得到∠FBC=∠FCA,∠AFB=∠AFC则,即可证明,推出;设,证明△ABG≌△ACK,得到,,即可推出∠ECK=∠K,得到EK=EC,则,由此即可得到答案.
【详解】解:延长EA到K,是的AK=AG,连接CK,
∵在三角形,,,
∴△ABC是等腰直角三角形,∠BAC=90°,
∴∠ACB=∠ABC=45°,
∵BF=FE,
∴∠FBE=∠FEB,
设∠BFE=x,则,
∵H是BC上中点,F是射线AH上一点,
∴AH⊥BC,
∴AH是线段BC的垂直平分线,∠FAC=45°,
∴CB=FC=FE,
∴∠FBC=∠FCA,∠AFB=∠AFC
∴,
∴,
∴,
∴,
∴,
∴,
设,
∵AG=AK,AB=AC,∠KAC=∠GAB=90°,
∴△ABG≌△ACK(SAS),
,,
∴,
∴∠ECK=∠K,
∴EK=EC,
∵,
∴,
∴,
故选D.
【点睛】本题主要考查了勾股定理和勾股定理的逆定理,等腰三角形的性质与判定,线段垂直平分线的性质与判定,全等三角形的性质与判定,三角形内角和定理等等,熟知相关知识是解题的关键.
10.(2022·浙江嘉兴·八年级期末)如图,在等腰中,,点P是内一点,且,,,以为直角边,点C为直角顶点,作等腰,下列结论:①点A与点D的距离为;②;③;④,其中正确结论有是( )
A.①②③ B.②④ C.①② D.②③④
【答案】C
【分析】连结AD,由等腰 ,可得AC=BC,等腰,可得CD=CP,由余角性质可∠DCA=∠PCB,可证△ADC≌△BPC(SAS)可判断①,由勾股定理DP=,再由,可证△ADP为等腰直角三角形,可判断②,由PB与PD可求BD=2,由勾股定理AB=,可判断③,由面积可判断④即可
【详解】解:连结AD,
在等腰中,,
∴AC=BC,
∵是等腰三角形,
∴CD=CP,
∴∠ACD+ACP=90°,∠ACP+∠PCB=90°,
∴∠DCA=∠PCB,
在△ADC和△BPC中,
AC=BC,
∠DCA=∠PCB,
DC=PC,
∴△ADC≌△BPC(SAS),
∴,
①点A与点D的距离为正确,
在Rt△DCP中,由勾股定理DP=,
在△ADP中,,
∴△ADP为等腰直角三角形,
∴AD⊥DP,
②正确;
BD=BP+PD=2,
在Rt△ADB中,由勾股定理,
AB=,
③不正确;
,
④不正确.
故选择:C.
【点睛】本题考查等腰直角三角形的性质与判定,三角形全等的判定与性质,三角形面积,勾股定理的应用,掌握等腰直角三角形的性质与判定,三角形全等的判定与性质,三角形面积,勾股定理的应用是解题关键.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·全国·八年级单元测试)在△ABC中,AB=c,AC=b,BC=a,当a、b、c满足_______时,∠B=90°.
【答案】a2+c2= b2
【分析】根据勾股定理的逆定理可得到满足的条件,可得到答案.
【详解】解:∵a2+c2=b2时,△ABC是以AC为斜边的直角三角形,
∴当a、b、c满足a2+c2=b2时,∠B=90°.
故答案为:a2+c2=b2.
【点睛】本题主要考查勾股定理的逆定理,掌握当两边平方和等于第三边的平方时第三边所对的角为直角是解题的关键.
12.(2021·天津市实验中学滨海学校八年级期中)在Rt△ABC中,斜边AB=5,直角边BC=3,则△ABC斜边上的高是________
【答案】
【分析】根据勾股定理及三角形的面积公式即可解答.
【详解】解:∵在Rt△ABC中,斜边AB=5,直角边BC=3,
∴另一直角边AC为:,
∴△ABC的面积=AB边上的高h=×AC×BC.
∴AB边上的高h=.
故答案为: .
【点睛】本题考查勾股定理,三角形面积,解决本题的关键是利用勾股定理求得另一直角边的长,比较简单.
13.(2022·山东莱芜·七年级期末)有一个三角形的两边长是1和,要使这个三角形成为直角三角形,则第三边边长的平方是______.
【答案】1或3
【分析】分第三边是直角边与斜边两种情况进行讨论,利用勾股定理即可求解.
【详解】解:当第三边是斜边时,第三边边长的平方是:12+()2=3;
当第三边是直角边时,第三边边长的平方是:()212=1;
故答案是:1或3.
【点睛】本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.分两种情况讨论是解题的关键.
14.(2022·全国·八年级单元测试)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为 ___.
【答案】4
【分析】设AQ=DQ=x,则BQ=AB﹣AQ=9﹣x,在Rt△BDQ中,用勾股定理列方程可解得x,从而可得答案.
【详解】解:∵BC=6,D是BC的中点,
∴BD=BC=3,
∵△ABC折叠,使A点与BC的中点D重合,
∴AQ=DQ,
设AQ=DQ=x,则BQ=AB﹣AQ=9﹣x,
在Rt△BDQ中,
∴
解得x=5,
∴BQ=9﹣x=4,
故答案为:4.
【点睛】本题考查折叠的性质和勾股定理,关键是利用方程思想设边长,然后用勾股定理列方程解未知数,求边长.
15.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,平面直角坐标系内有一点A(2,-2),点O是原点,点P是x轴上一动点,如果以P、O、A为顶点的三角形是等腰三角形,那么点P的坐标为_______.
【答案】(,0)或(4,0)或(-2,0)或(2,0)
【分析】根据题意分类讨论,①OA为等腰三角形底边,②OA为等腰三角形一条腰,根据等腰三角形的性质求解即可.
【详解】解:设,
A(2,-2)
如图:①OA为等腰三角形底边,
即
解得
符合条件的动点P有一个,即(2,0);
②OA为等腰三角形一条腰,
当时,
即
解得
当时,
解得或(舍去)
符合符合条件的动点P有三个即(-2,0),(2,0),(4,0).
综上所述,符合条件的点P的坐标是:(,0)或(4,0)或(-2,0)或(2,0).
故答案为:(,0)或(4,0)或(-2,0)或(2,0).
【点睛】此题主要考查了等腰三角形的判定及坐标与图形的性质;利用等腰三角形的判定来解决实际问题,其关键是根据题意,画出符合实际条件的图形,根据等腰三角形的性质求解.
16.(2022·全国·八年级单元测试)如图,每个小正方形的边长都相等,,,是小正方形的顶点,则的度数为______.
【答案】
【分析】连接 ,设小正方形的边长为 ,由勾股定理可得 , ,再由勾股定理逆定理可得 ,即可求解.
【详解】解:如图,连接 ,
设小正方形的边长为 ,由勾股定理得:
,
,
,
∴ , ,
∴ , ,
∴ .
故答案为:.
【点睛】本题主要考查了勾股定理及逆定理,等腰三角形的性质,根据勾股定理得出 、 、 是解题的关键.
17.(2021·四川内江·八年级期末)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC A沿CE翻折,使点A落在AB上的点D处;再将边 BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点 E、F,则△B'FC 的面积为______________.
【答案】
【分析】由题意可得AB=10,根据面积可得CE=4.8,根据勾股定理可求BE=6.4,由折叠可求∠ECF=45°,可得EC=EF=4.8,即可求BF的长,可求面积.
【详解】解:∵Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴BA= =10,
∵将边AC沿CE翻折,使点A落在AB上的点D处,
∴∠AEC=∠CED,∠ACE=∠DCE,
∵∠AED=180°,
∴∠CED=90°,即CE⊥AB,
∵S△ABC= AB×EC=AC×BC,
∴EC=4.8,
在Rt△BCE中,BE==6.4,
∵将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,
∴BF=B'F,∠BCF=∠B'CF,
∵∠BCF+∠B'CF+∠ACE+∠DCE=∠ACB=90°,
∴ECF=45°,
又CE⊥AB,
∴∠EFC=∠ECF=45°,
∴CE=EF=4.8,
∵BF=BE-EF=6.4-4.8=1.6,
∴△BFC的面积为:FB×EC=,
由翻折可知,△B'FC 的面积=△BFC的面积=
故答案为.
【点睛】本题考查了折叠问题,勾股定理,根据折叠的性质求∠ECF=45°是本题的关键.
18.(2022·广东龙华·八年级期末)如图1,动点P从长方形ABCD的顶点A出发,沿A→C→D以1cm/s的速度运动到点D停止.设点P的运动时间为x(s),△PAB的面积为y(cm2).表示y与x的函数关系的图象如图2所示,则长方形ABCD的面积为 _____cm2.
【答案】60
【分析】根据题意可得AC=13cm,CD=25-13=12(cm),根据勾股定理可得AD的值,进而得出长方形ABCD的面积.
【详解】解:由图象,结合题意可得AC=13cm,CD=25-13=12(cm),
∴AD==5(cm),
∴长方形ABCD的面积为:12×5=60(cm2).
故答案为:60.
【点睛】本题考查了动点问题的函数图象,解决本题应首先看清横轴和纵轴表示的量.
三、解答题:本题共7个小题,19-23每题7分,24小题9分,25每题12分,共56分。
19.(2022·广东·深圳市福田区第二实验学校八年级期中)如图,在△ABC中,AB=4,BC=,点D在AB上,且BD=1,CD=2.
(1)求证:CD⊥AB;
(2)求AC的长.
【答案】(1)见解析;(2)
【分析】
(1)根据勾股定理逆定理证明△BCD是直角三角形,即可得证;
(2)先求得AD=,在Rt△ACD中,勾股定理求解即可.
【详解】解:(1)证明:∵在△BCD中,BD=1,CD=2,BC=,
∴BD2+CD2=12+22=()2=BC2,
∴△BCD是直角三角形,且∠CDB=90°,
∴CD⊥AB;
(2)
解:∵CD⊥AB,
∴∠ADC=90°,
∵AB=4,DB=1,
∴AD=3,
在Rt△ACD中,∵CD=2,
∴AC===,
∴AC的长为.
【点睛】本题考查了勾股定理以及勾股定理的逆定理,掌握勾股定理是解题的关键.
20.(2021·全国·八年级单元测试)在中,.
(1)如图1,点在线段上,,求的度数;
(2)点在线段上(不与点重合),,点Q关于直线的对称点为M,连接.
①依题意将图2补全;
②用等式表示线段之间的数量关系,并证明.
【答案】(1);(2)①见解析;②,证明见解析
【分析】
(1)根据三角形的外角性质和等腰三角形的性质可以得解;
(2)①根据轴对称的意义和性质可以作出图形;
②连结MC,然后根据轴对称的性质和直角等腰三角形的性质以及三角形全等的判定和性质可以得到解答.
【详解】解:(1)∵在中,,
.
是的一个外角,
.
,
.
,
.
(2)①如图,由题意可得补全图如下:
②,理由如下:
如上图,连接.
,
.
,
.
.
.
.
∵点Q关于直线的对称点为M,
.
,
∴△ABP≌△ACM,
∴BP=CM,
.
在中,,
.
,
.
在中,,
,
【点睛】本题考查直角三角形的综合应用,熟练掌握直角等腰三角形和三角形的性质、轴对称的意义和性质、三角形全等的判定和性质以及勾股定理的应用是解题关键.
21.(2022·广东·深圳市西乡中学八年级期中)在长方形ABCD中,截取如图所示的阴影部分,已知EC=5,CF=5,FG=4,EG=3,∠EGF=90°.
(1)连接EF,求证:∠FEC=90°;
(2)求出图中阴影部分的面积.
【答案】(1)见解析;(2)
【分析】
(1)先求EF,再利用勾股定理的逆定理得出△EFC为直角三角形,即可得证;
(2)先求出和的面积,再利用得出阴影部分的面积.
【详解】解:(1)∵∠EGF=90°,根据勾股定理得:
EF=,
∵,,
∴,
∴△EFC为直角三角形,
∴∠FEC=90°;
(2)∵,,
∴.
【点睛】本题考查了勾股定理及其逆定理,灵活运用勾股定理是解题的关键.
22.(2021·陕西·交大附中分校七年级期末)某运动公园有一块空地,如图,△ABC所示,∠ACB=90°,公园管理处计划在△ADC区域内安装健身器材,其余部分种植草坪,绿化环境.经测量:CD=30米,AD=40米,BC=120米,AB=130米.
(1)求证:∠ADC=90°;
(2)若种植草坪的费用每平方米300元,求种植草坪的总费用.
【答案】(1)见解析;(2)720000元
【分析】
(1)首先在中利用勾股定理求出AC的长,再利用勾股定理逆定理证明为直角三角形,即可证得;
(2)用S阴影,分别计算出两个直角三角形的面积代入即可.
【详解】解:(1)证明:在中,
∵,
∴,
又∵,
∴,
∴是直角三角形,
∴;
(2)S阴影
(平方米),
总费用:(元)
答:种植草坪的总费用是720000元.
【点睛】本题考查勾股定理及其逆定理的应用,利用勾股定理的逆定理证明直角三角形是解题的关键.
23.(2021·江苏靖江·八年级期末)如图,某公园有两个小喷泉A、B,两个小喷泉之间的距离为25m.现要为喷泉铺设供水管道AM、BM,供水点M在小路AC上,供水点M到AB的距离MN的长为12m,BM的长为15m.
(1)求供水点M到喷泉A、B需要铺设的管道总长;
(2)试判断BM是否是喷泉B到小路AC的最短距离,若是,请说明理由;若不是,请求出最短距离.
【答案】(1)供水点M到喷泉A、B铺设的管道总长为35m;(2)是到小路的最短距离,见解析.
【分析】
(1)在中,利用勾股定理解得的长,继而解得的长,在中,利用勾股定理解得的长,据此解题;
(2)根据勾股定理的逆定理证明是直角三角形,再结合垂线段最短性质解题.
【详解】解:(1)∵
∴
在中,
∴
∴
在中
∴
答:供水点M到喷泉A、B铺设的管道总长为35m.
(2)是到小路的最短距离,
∵,
∴是直角三角形
根据垂线段最短性质,得
是到小路的最短距离.
【点睛】本题考查勾股定理及其逆定理的应用、垂线段最短等知识,是重要考点,难度较易,掌握相关知识是解题关键.
24.(2021·全国·八年级单元测试)在四边形中,,为边上的点.
(1)连接,,;
①如图,若,求证:;
②如图,若,求证:平分;
(2)如图,是的平分线上的点,连接,,若,,,求的长.
【答案】(1)①见解析;②见解析;(2).
【分析】
(1)①根据条件得出,即可求证;
②延长交的延长线于点,得出再证明即可;
(2)解法1:过点分别作,,得到,由,,得到,设,求得,在和中,由勾股定理即可求得的长.
解法2:在上截取,得出,过作,根据,即可求得的长.
【详解】解:(1)①证明:,
,,
,
在和中
,,,
,
.
②证明:延长交的延长线于点,
,
,,
,
,
,
,
,
,
,
,
平分.
(2)解法1:如图,过点分别作,,分别交及的延长线于点,.
平分,
,
又,,
,
在和中
,,,
,
,,
在和中
,,,
,
设,
,,
,,
,
,
,
,
在和中
,,,
.
解法2:如图,在上截取,
,,
,
在和中
,,,
,
,
,
,
过作,垂足为,
,
,
在和中
.
【点睛】本题主要考查了全等三角形的判定和性质,角平分线的判定,以及勾股定理的应用,解题的关键是熟练掌握全等三角形的判定和性质,正确作出辅助线以及利用方程解决问题.
25.(2022·湖北汉阳·八年级期末)已知中,如果过项点的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为的关于点的二分割线.例如:如图1,中,,,若过顶点的一条直线交于点,若,显然直线是的关于点的二分割线.
(1)在图2的中,,.请在图2中画出关于点的二分割线,且角度是 ;
(2)已知,在图3中画出不同于图1,图2的,所画同时满足:①为最小角;②存在关于点的二分割线.的度数是 ;
(3)已知,同时满足:①为最小角;②存在关于点的二分割线.请求出的度数(用表示).
【答案】(1)作图见解析,;(2)作图见解析,;(3)∠A=45°或90°或90°-2α或,或α=45°时45°<∠BAC<90°.
【分析】
(1)根据二分割线的定义,只要把∠ABC分成90°角和20°角即可;
(2)可以画出∠A=35°的三角形;
(3)设BD为△ABC的二分割线,分以下两种情况.第一种情况:△BDC是等腰三角形,△ABD是直角三角形;第二种情况:△BDC是直角三角形,△ABD是等腰三角形分别利用直角三角形的性质、等腰三角形的性质和三角形的内角和定理解答即可.
【详解】解:(1)关于点的二分割线BD如图4所示,;
故答案为:20°;
(2)如图所示:∠BAC=35°;
(3)设BD为△ABC的二分割线,分以下两种情况.
第一种情况:△BDC是等腰三角形,△ABD是直角三角形,易知∠C和∠DBC必为底角,
∴∠DBC=∠C=.
当∠A=90°时,△ABC存在二分分割线;
当∠ABD=90°时,△ABC存在二分分割线,此时∠A=90°-2α;
当∠ADB=90°时,△ABC存在二分割线,此时α=45°且45°<∠A<90°;
第二种情况:△BDC是直角三角形,△ABD是等腰三角形,
当∠DBC=90°时,若BD=AD,则△ABC存在二分割线,此时;
当∠BDC=90°时,若BD=AD,则△ABC存在二分割线,此时∠A=45°,
综上,∠A=45°或90°或90°-2α或,或α=45°时,45°<∠BAC<90°.
【点睛】本题考查的是二分割线的理解与作图,属于新定义题型,主要考查了等腰三角形的性质、直角三角形的性质和三角形的内角和定理等知识,正确理解二分割线的定义、熟练掌握等腰三角形和直角三角形的性质是解答的关键.
