2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2.4组合数课件(17张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2.4组合数课件(17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 391.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-24 15:32:30 | ||
图片预览




文档简介
(共17张PPT)
6.2.4 组合数
(1)能在组合基础上给出组合数的定义和表示,并能区别组合与组合数。
(2)通过探索排列与组合的关系,得到求组合数的方法;
(3)能利用组合数公式解决一些简单的组合问题;
(4)通过组合数的计算,体会“数学运算”;通过探索排列与组合的关系,体会“逻辑推理”.
重点:组合数公式。
难点:推导和应用组合数公式.
学习目标:
问题1:在6.2.3节中,我们通过列举数数的方式得到各问题的组合个数,但随着元素个数的增加,这样的方法就越来越烦琐了。是否能像排列一样,也能找到计算组合个数的公式,从而能便捷地求出组合个数?
追问1:用组合数符号表示6.2.3节问题1的组合数,并说明组合数与组合有何区别.
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,有多少种不同的选法?
“一个组合”是指“从n个不同元素中取出m(m≤n)个元素合成一组”,它不是一个数;
“组合数”是指“从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数”,它是一个非零自然数.
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
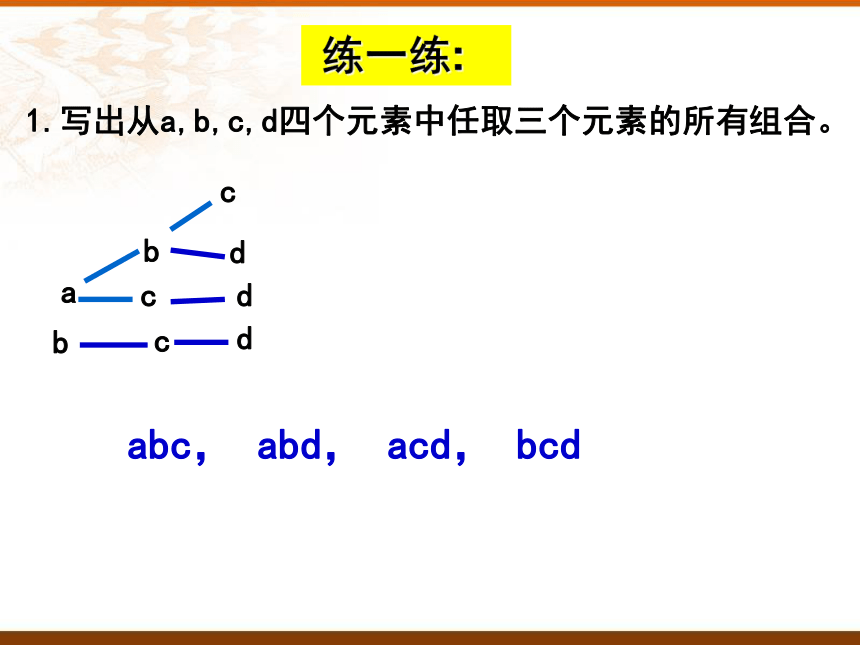
1.写出从a,b,c,d四个元素中任取三个元素的所有组合。
abc, abd, acd, bcd
b
c
d
d
c
b
a
c
d
练一练:
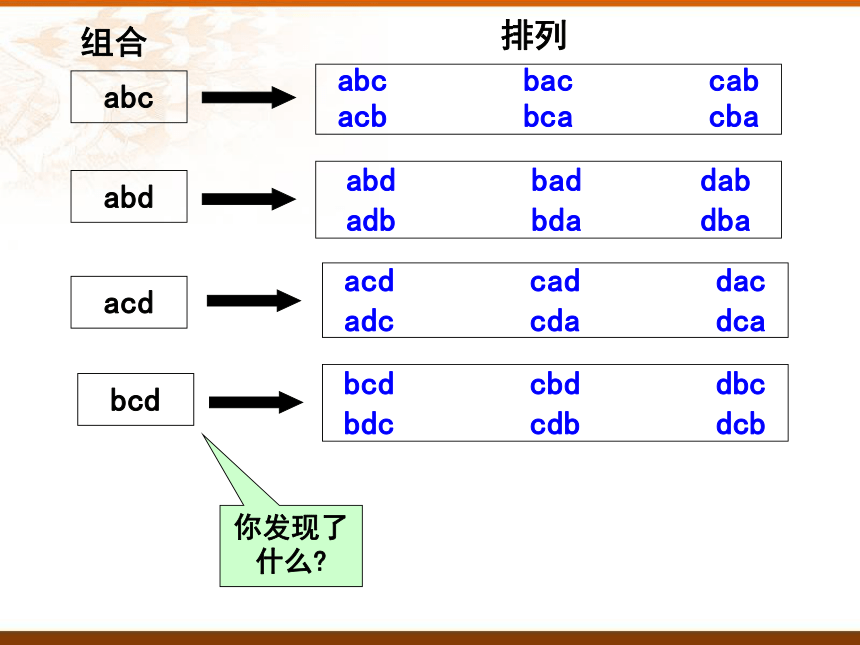
组合
排列
abc
abd
acd
bcd
abc bac cab
acb bca cba
abd bad dab
adb bda dba
acd cad dac
adc cda dca
bcd cbd dbc
bdc cdb dcb
你发现了什么
如何计算:
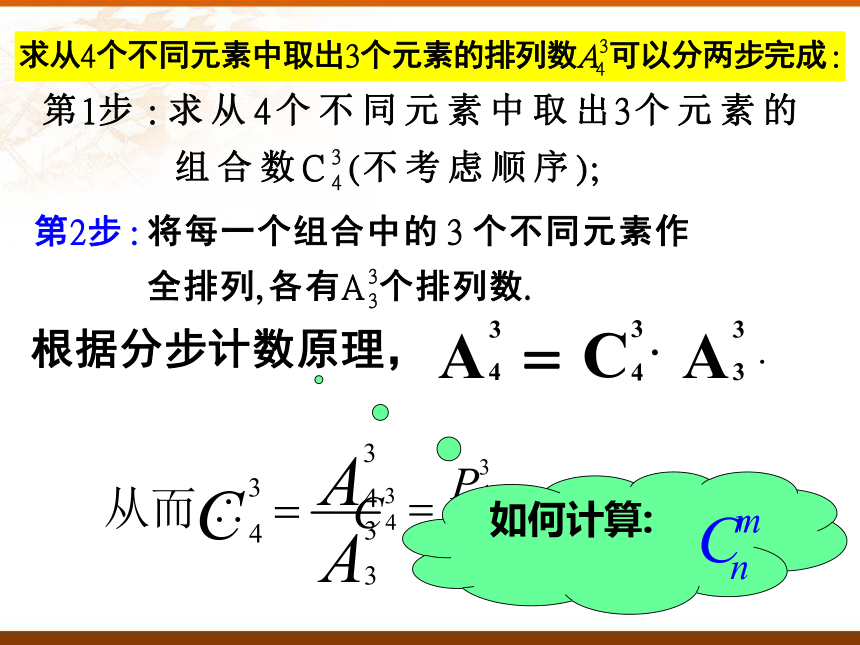
根据分步计数原理,得到:
因此:
一般地,求从 个不同元素中取出 个元素的排列数,可以分为以下2步:
第1步,先求出从这 个不同元素中取出 个元素的组合数 .
第2步,求每一个组合中 个元素的全排列数 .
这里 ,且 ,这个公式叫做组合数公式.
例6:计算:(1) ;(2) ;(3) ;(4)
解:
思考:分别观察例中(1)与(2),(3)与(4)的结果,你有什么发现和猜想?
证明:
证明:
请看课本P25:练习1
1.某校开设A类选修课3门,B类选修课5门,一位同学要从中选3门.若要求A类课程中至少选1门,则不同的选法共有( )
A.15种 B.30种 C.45种 D.46种
D
学以致用:
2.在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各数位之和为偶数的共有( )
A.36个 B.24个 C.18个 D.6个
3.从进入决赛的6名选手中决出1名一等奖、2名二等奖、3名三等奖,则可能的决赛结果共有____种
A
60
学以致用:
4.某班级要从4名女生、2名男生中派4人参加某活动,如果要求至少有1名男生,那么不同的选派方案种数为________
5.用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有________ 个(用数字作答).
14
1080
学以致用:
6.某医院从10名医疗专家中抽调6名组成医疗小组到社区义诊,其中这10名医疗专家中有4名是外科专家.问:
(1)抽调的6名专家中恰有2名是外科专家的抽调方法有多少种?
(2)至少有2名外科专家的抽调方法有多少种?
(3)至多有2名外科专家的抽调方法有多少种?
90
185
115
学以致用:
7.6本不同的书,分为3组,在下列条件下各有多少种不同的分配方法?
(1)每组2本(平均分组);
(2)一组1本,一组2本,一组3本(不平均分组);
(3)一组4本,另外两组各1本(局部平均分组).
15
60
15
学以致用:
6.2.4 组合数
(1)能在组合基础上给出组合数的定义和表示,并能区别组合与组合数。
(2)通过探索排列与组合的关系,得到求组合数的方法;
(3)能利用组合数公式解决一些简单的组合问题;
(4)通过组合数的计算,体会“数学运算”;通过探索排列与组合的关系,体会“逻辑推理”.
重点:组合数公式。
难点:推导和应用组合数公式.
学习目标:
问题1:在6.2.3节中,我们通过列举数数的方式得到各问题的组合个数,但随着元素个数的增加,这样的方法就越来越烦琐了。是否能像排列一样,也能找到计算组合个数的公式,从而能便捷地求出组合个数?
追问1:用组合数符号表示6.2.3节问题1的组合数,并说明组合数与组合有何区别.
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,有多少种不同的选法?
“一个组合”是指“从n个不同元素中取出m(m≤n)个元素合成一组”,它不是一个数;
“组合数”是指“从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数”,它是一个非零自然数.
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
1.写出从a,b,c,d四个元素中任取三个元素的所有组合。
abc, abd, acd, bcd
b
c
d
d
c
b
a
c
d
练一练:
组合
排列
abc
abd
acd
bcd
abc bac cab
acb bca cba
abd bad dab
adb bda dba
acd cad dac
adc cda dca
bcd cbd dbc
bdc cdb dcb
你发现了什么
如何计算:
根据分步计数原理,得到:
因此:
一般地,求从 个不同元素中取出 个元素的排列数,可以分为以下2步:
第1步,先求出从这 个不同元素中取出 个元素的组合数 .
第2步,求每一个组合中 个元素的全排列数 .
这里 ,且 ,这个公式叫做组合数公式.
例6:计算:(1) ;(2) ;(3) ;(4)
解:
思考:分别观察例中(1)与(2),(3)与(4)的结果,你有什么发现和猜想?
证明:
证明:
请看课本P25:练习1
1.某校开设A类选修课3门,B类选修课5门,一位同学要从中选3门.若要求A类课程中至少选1门,则不同的选法共有( )
A.15种 B.30种 C.45种 D.46种
D
学以致用:
2.在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各数位之和为偶数的共有( )
A.36个 B.24个 C.18个 D.6个
3.从进入决赛的6名选手中决出1名一等奖、2名二等奖、3名三等奖,则可能的决赛结果共有____种
A
60
学以致用:
4.某班级要从4名女生、2名男生中派4人参加某活动,如果要求至少有1名男生,那么不同的选派方案种数为________
5.用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有________ 个(用数字作答).
14
1080
学以致用:
6.某医院从10名医疗专家中抽调6名组成医疗小组到社区义诊,其中这10名医疗专家中有4名是外科专家.问:
(1)抽调的6名专家中恰有2名是外科专家的抽调方法有多少种?
(2)至少有2名外科专家的抽调方法有多少种?
(3)至多有2名外科专家的抽调方法有多少种?
90
185
115
学以致用:
7.6本不同的书,分为3组,在下列条件下各有多少种不同的分配方法?
(1)每组2本(平均分组);
(2)一组1本,一组2本,一组3本(不平均分组);
(3)一组4本,另外两组各1本(局部平均分组).
15
60
15
学以致用:
