青岛版八年级数学上册1.1 全等三角形 教学课件(共27张PPT)
文档属性
| 名称 | 青岛版八年级数学上册1.1 全等三角形 教学课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
情境引入
04
例题精讲
1.了解全等形的概念,知道全等形的形状相同,大小相同.
2.掌握全等三角形的相关概念及表示法,知道全等三角形的性质:全等三角形对应边相等,对应角相等.
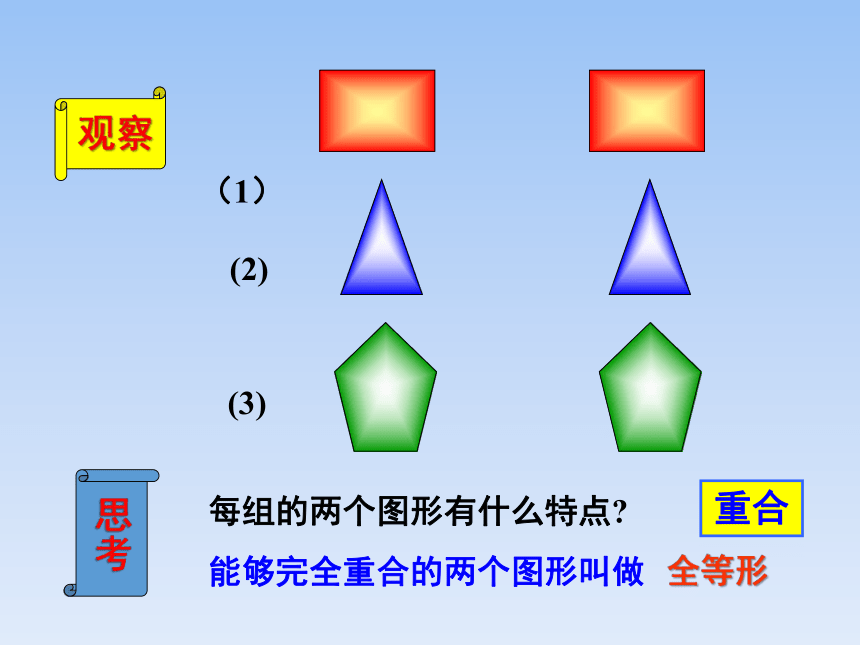
我们已经学习了三角形,那么在下面这些图中,有许许多多的三角形,你能从中找到形状和大小都相同的三角形吗?
(1)
(2)
(3)
思考
每组的两个图形有什么特点
观察
重合
能够完全重合的两个图形叫做
全等形
形状
相同
大小
相同
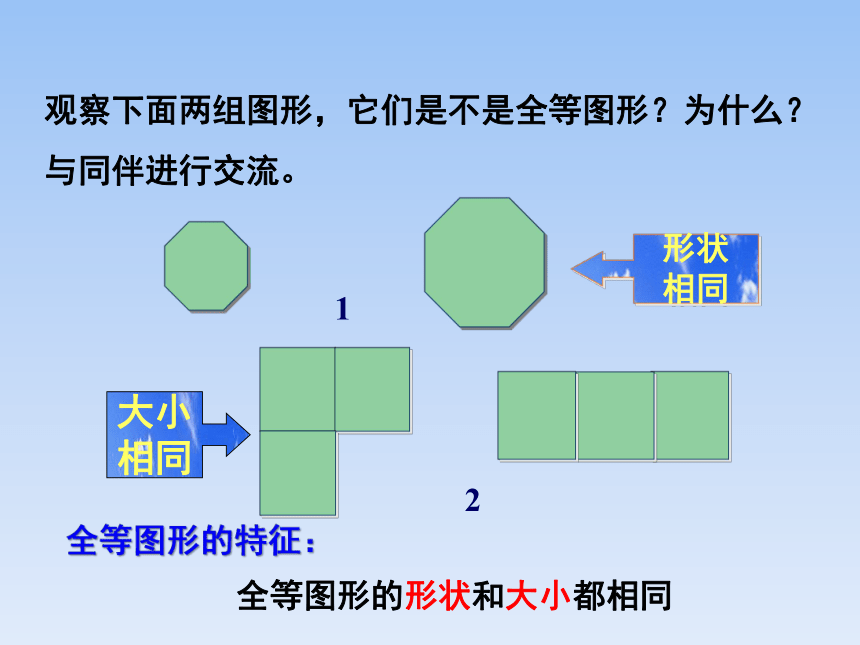
观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
1
2
全等图形的特征:
全等图形的形状和大小都相同
同一张底片洗出的尺寸相同的照片是能够完全重合的
全等形包括规则图形和不规则图形全等
A
B
C
E
D
F
能够完全重合的两个三角形,叫
全等三角形.
记作:△ABC≌△DEF
读作 :△ABC全等于△DEF
注意:书写全等式时要求
把对应顶点字母放
在对应的位置上.
“全等”用符号“ ”来表示,读作“ ”
≌
全等于
A
B
C
D
E
F
互相重合的边叫做对应边
互相重合的顶点叫做对应顶点
互相重合的角叫做对应角
A D
B E
C F
AB与DE
BC与EF
AC与DF
∠A与∠D
∠B与∠E
∠C与∠F
提示:登录优教同步学习网,搜索动画演示:全等三角形及其性质
(全等三角形的对应角相等)
A
B
C
D
E
F
1、全等三角形的对应边相等,
2、全等三角形的对应角相等。
(已知)
(全等三角形的对应边相等)
∴ AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的性质:
∵△ABC≌△DEF
A
B
C
D
E
F
先写出全等式,再指出它们的对应边和对应角
例1:
∵△ABC≌△DEF
∴AB和DE,BC和EF,AC和DF分别是对应边.
∴∠A和∠D,∠B和∠E,∠C和∠F分别是对应角.
A
B
C
D
先写出全等式,再指出它们的对应边
和对应角
试一试1:
∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,
∠ABC=∠ABD
∠C= ∠D.
规律一:有公共边的,公共边是对应边
先写出全等式,再指出它们的对应边
和对应角
试一试2:
A
C
O
D
B
∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.
规律二:有对顶角的,对顶角是对应角
A
B
C
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试3:
∵△ABC≌△ADE
∴AB=AD,AC=AE,BC=DE
∴∠A=∠A,∠B=∠D,
∠ACB= ∠AED.
规律三:有公共角的,公共角是对应角
例2:如图,已知ΔABC≌ΔDEF,写出这两个三角形中相等的边和相等的角 .
解: 由ΔABC≌ΔDEF可知,这两个三角形的对应边分别相等,所以AB=DE,AC=DF,BC=EF.
D
A
B
C
E
F
它们的对应角分别相等,所以∠A=∠D,∠B=∠E
∠ACB=∠DFE.
A
B
C
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试4:
∵△ABC≌△DEC
∴AB=DE,AC=DC,
BC=EC
∴∠A=∠D,
∠B=∠E,
∠ACB= ∠DCE.
规律四:一对最长的边是对应边
一对最短的边是对应边
A
D
E
B
C
A
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试5:
∵△ABC≌△FDE
∴AB=FD,AC=FE,
BC=DE
∴∠A=∠F,
∠B=∠D,
∠ACB= ∠FED.
规律五:一对最大的角是对应角
一对最小的角是对应角
1、请指出下列全等三角形的对应边和对应角
1、 △ ABE ≌ △ ACF
对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。
2、 △ BCE ≌ △ CBF
对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。
3、 △ BOF ≌ △ COE
对应角是: ∠BOF和∠COE、 ∠BFO 和∠CEO、 ∠ FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。
2、如图,若ΔOAD≌ΔOBC, 且∠O=65°,
∠C=20°,则∠OAD= .
分析:
由∠O=65°,∠C=20°知:
∠OBC=95 °,
由ΔOAD≌ΔOBC知: ∠OAD=95 ° .
95 °
3、如图,已知ΔABD≌ΔAEC, ∠B和∠E是对应角,AB与AE是对应边,试说明:BC=DE.
分析: 因为ΔABD≌ΔAEC并且∠B和∠E是对应角,
所以AD和AC是对应边,又因为AB与AE是对应边,
所以BD和EC是对应边,即BD=EC,
所以BD-CD=EC-CD,
所以BC=DE.
4、如图,已知ΔABE≌ΔACD,且∠1=∠2, ∠B=∠C,请指出其余的对应边和对应角.
分析:由ΔABE≌ΔACD以及∠1=∠2, ∠B=∠C知:
∠ BAE与∠CAD是对应角,
根据“对应角的对边是对应边 ”可知:AB与AC,AE与AD,
BE与CD分别是对应边.
2. 叫做全等三角形。
1.能够重合的两个图形叫做
全等形
4.全等三角形的 和 相等;
对应边
对应角
对应顶点
课 堂 小 结
能够重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应的位置上.
全等于
≌
其中:互相重合的顶点叫做___
互相重合的边叫做____
互相重合的角叫做___
总结:寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,
最小的边是对应边;
(5)两个全等三角形最大的角是对应角,
最小的角是对应角;
作业:
1.习题1.1
2.思考:
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
情境引入
04
例题精讲
1.了解全等形的概念,知道全等形的形状相同,大小相同.
2.掌握全等三角形的相关概念及表示法,知道全等三角形的性质:全等三角形对应边相等,对应角相等.
我们已经学习了三角形,那么在下面这些图中,有许许多多的三角形,你能从中找到形状和大小都相同的三角形吗?
(1)
(2)
(3)
思考
每组的两个图形有什么特点
观察
重合
能够完全重合的两个图形叫做
全等形
形状
相同
大小
相同
观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
1
2
全等图形的特征:
全等图形的形状和大小都相同
同一张底片洗出的尺寸相同的照片是能够完全重合的
全等形包括规则图形和不规则图形全等
A
B
C
E
D
F
能够完全重合的两个三角形,叫
全等三角形.
记作:△ABC≌△DEF
读作 :△ABC全等于△DEF
注意:书写全等式时要求
把对应顶点字母放
在对应的位置上.
“全等”用符号“ ”来表示,读作“ ”
≌
全等于
A
B
C
D
E
F
互相重合的边叫做对应边
互相重合的顶点叫做对应顶点
互相重合的角叫做对应角
A D
B E
C F
AB与DE
BC与EF
AC与DF
∠A与∠D
∠B与∠E
∠C与∠F
提示:登录优教同步学习网,搜索动画演示:全等三角形及其性质
(全等三角形的对应角相等)
A
B
C
D
E
F
1、全等三角形的对应边相等,
2、全等三角形的对应角相等。
(已知)
(全等三角形的对应边相等)
∴ AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的性质:
∵△ABC≌△DEF
A
B
C
D
E
F
先写出全等式,再指出它们的对应边和对应角
例1:
∵△ABC≌△DEF
∴AB和DE,BC和EF,AC和DF分别是对应边.
∴∠A和∠D,∠B和∠E,∠C和∠F分别是对应角.
A
B
C
D
先写出全等式,再指出它们的对应边
和对应角
试一试1:
∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,
∠ABC=∠ABD
∠C= ∠D.
规律一:有公共边的,公共边是对应边
先写出全等式,再指出它们的对应边
和对应角
试一试2:
A
C
O
D
B
∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.
规律二:有对顶角的,对顶角是对应角
A
B
C
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试3:
∵△ABC≌△ADE
∴AB=AD,AC=AE,BC=DE
∴∠A=∠A,∠B=∠D,
∠ACB= ∠AED.
规律三:有公共角的,公共角是对应角
例2:如图,已知ΔABC≌ΔDEF,写出这两个三角形中相等的边和相等的角 .
解: 由ΔABC≌ΔDEF可知,这两个三角形的对应边分别相等,所以AB=DE,AC=DF,BC=EF.
D
A
B
C
E
F
它们的对应角分别相等,所以∠A=∠D,∠B=∠E
∠ACB=∠DFE.
A
B
C
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试4:
∵△ABC≌△DEC
∴AB=DE,AC=DC,
BC=EC
∴∠A=∠D,
∠B=∠E,
∠ACB= ∠DCE.
规律四:一对最长的边是对应边
一对最短的边是对应边
A
D
E
B
C
A
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试5:
∵△ABC≌△FDE
∴AB=FD,AC=FE,
BC=DE
∴∠A=∠F,
∠B=∠D,
∠ACB= ∠FED.
规律五:一对最大的角是对应角
一对最小的角是对应角
1、请指出下列全等三角形的对应边和对应角
1、 △ ABE ≌ △ ACF
对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。
2、 △ BCE ≌ △ CBF
对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。
3、 △ BOF ≌ △ COE
对应角是: ∠BOF和∠COE、 ∠BFO 和∠CEO、 ∠ FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。
2、如图,若ΔOAD≌ΔOBC, 且∠O=65°,
∠C=20°,则∠OAD= .
分析:
由∠O=65°,∠C=20°知:
∠OBC=95 °,
由ΔOAD≌ΔOBC知: ∠OAD=95 ° .
95 °
3、如图,已知ΔABD≌ΔAEC, ∠B和∠E是对应角,AB与AE是对应边,试说明:BC=DE.
分析: 因为ΔABD≌ΔAEC并且∠B和∠E是对应角,
所以AD和AC是对应边,又因为AB与AE是对应边,
所以BD和EC是对应边,即BD=EC,
所以BD-CD=EC-CD,
所以BC=DE.
4、如图,已知ΔABE≌ΔACD,且∠1=∠2, ∠B=∠C,请指出其余的对应边和对应角.
分析:由ΔABE≌ΔACD以及∠1=∠2, ∠B=∠C知:
∠ BAE与∠CAD是对应角,
根据“对应角的对边是对应边 ”可知:AB与AC,AE与AD,
BE与CD分别是对应边.
2. 叫做全等三角形。
1.能够重合的两个图形叫做
全等形
4.全等三角形的 和 相等;
对应边
对应角
对应顶点
课 堂 小 结
能够重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应的位置上.
全等于
≌
其中:互相重合的顶点叫做___
互相重合的边叫做____
互相重合的角叫做___
总结:寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,
最小的边是对应边;
(5)两个全等三角形最大的角是对应角,
最小的角是对应角;
作业:
1.习题1.1
2.思考:
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
