青岛版八年级数学上册1.2.1怎样判定三角形全等 教学课件(共20张PPT)
文档属性
| 名称 | 青岛版八年级数学上册1.2.1怎样判定三角形全等 教学课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
旧知回顾
04
例题精讲
1.通过实验探究得到全等三角形的判定定理1:两边及其夹角分别相等的两个三角形全等.
2.会用判定定理1解决相关的证明与计算问题.
1.什么叫做全等形,全等形有什么特征?
2.什么叫做全等三角形,全等三角形对应边和对应角有什么特点?
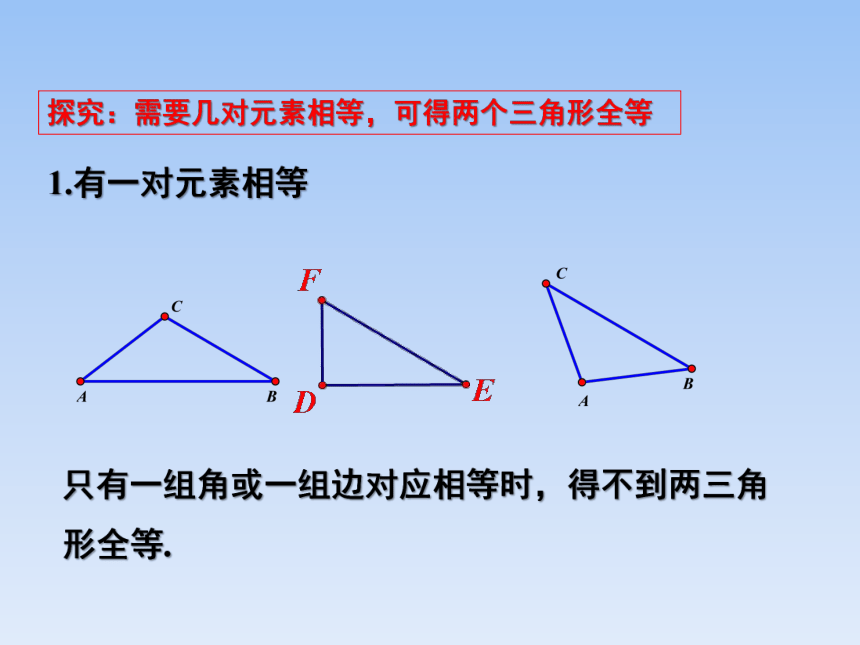
1.有一对元素相等
探究:需要几对元素相等,可得两个三角形全等
只有一组角或一组边对应相等时,得不到两三角形全等.
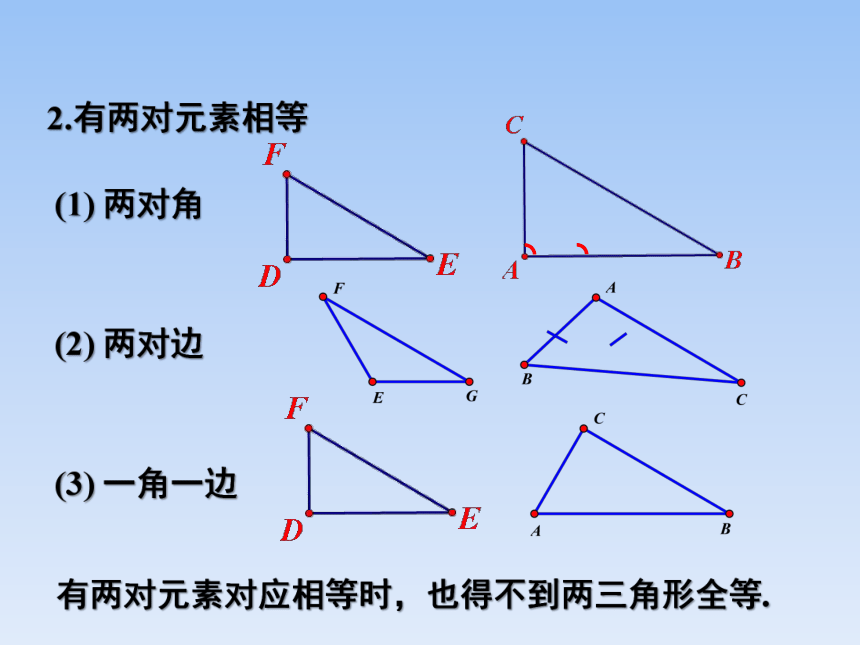
2.有两对元素相等
有两对元素对应相等时,也得不到两三角形全等.
(1) 两对角
(2) 两对边
(3) 一角一边
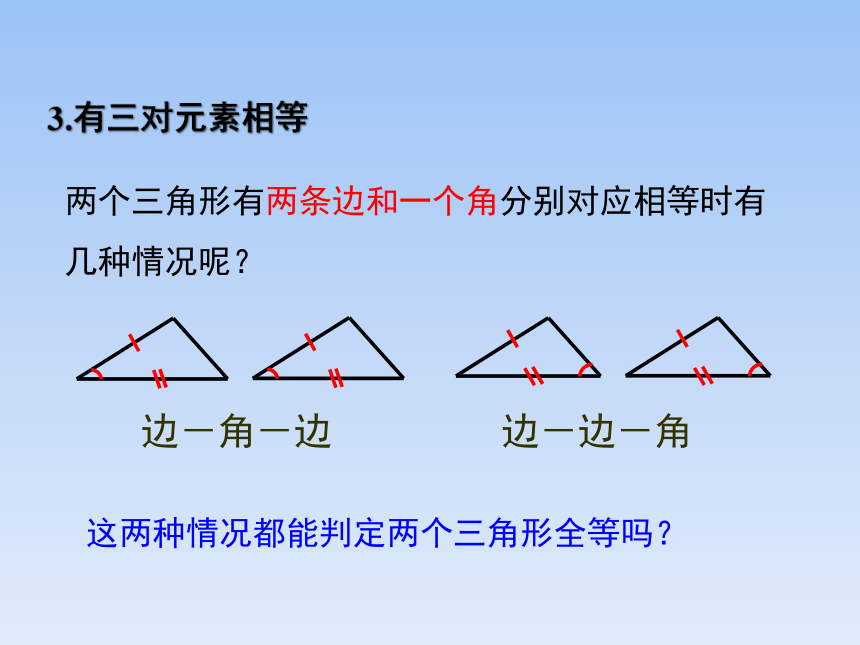
3.有三对元素相等
两个三角形有两条边和一个角分别对应相等时有几种情况呢?
边-角-边
边-边-角
这两种情况都能判定两个三角形全等吗?
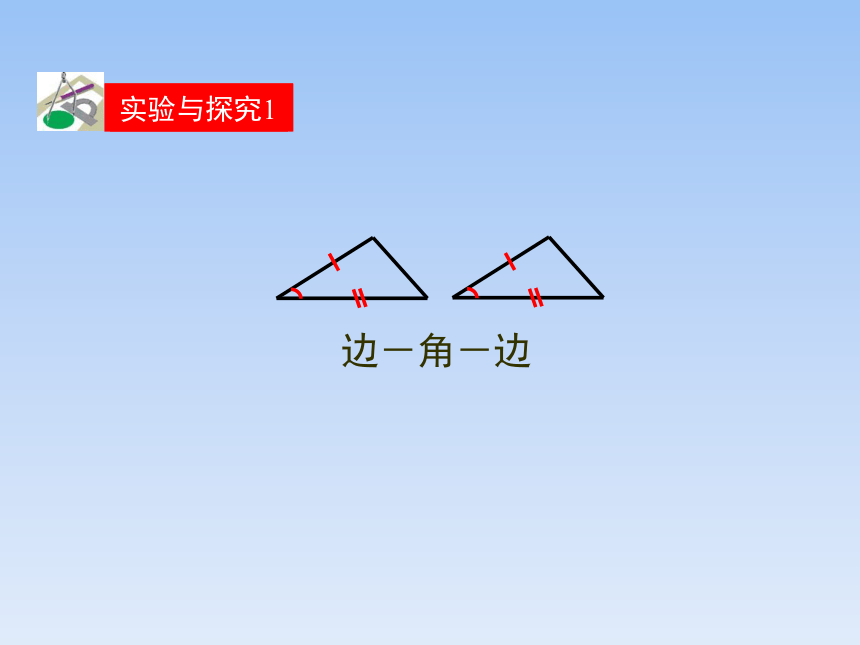
实验与探究1
边-角-边
B
A
C
用符号语言表达为:
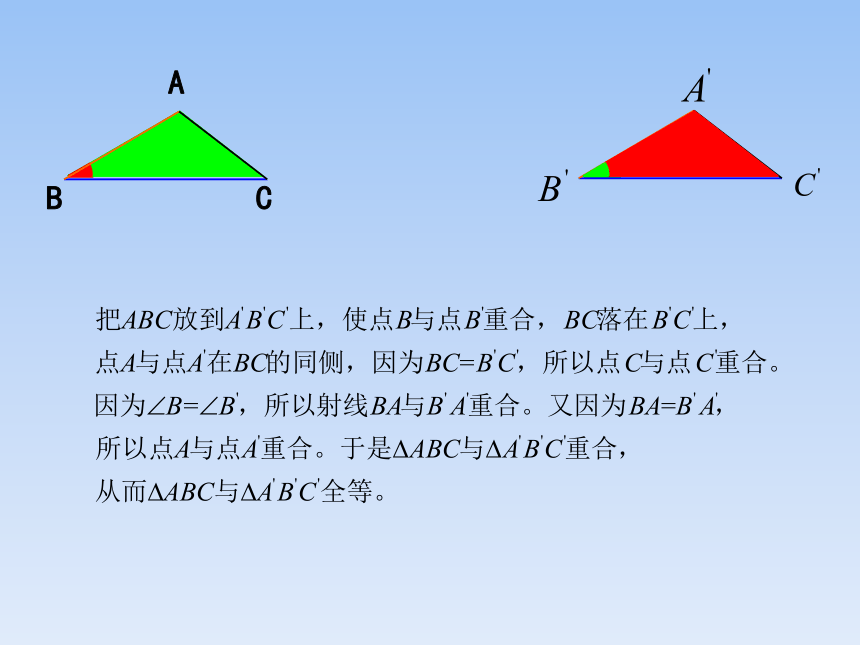
在△ABC与△ A′B′C′中:
AB=A′B′,∠B=∠B′,BC= B′C′
∴△ABC≌△ A′B′C′(SAS)
A
B
C
A′
B′
C′
判定方法1 两边及其夹角分别相等的两个三角形全等.
这个判定方法通常简写成“边角边”或“SAS”.
提示:登录优教同步学习网,搜索动画演示:两个三角形全等的判定方法(SAS)
如图,下列三角形中,哪两个三角形是全等三角形?
4
5
30。
①
40。
6
4
②
40。
6
4
③
4
5
40。
④
D
E
A
B
C
F
想一想
实验与探究2
边-边-角
例1 如图1-10,已知AB=AD,
∠BAC=∠DAC,△ABC与△ADC全等吗?说明你的理由.
解: △ABC与△ADC全等.理由是:
在△ABC与△ADC中,
∵ AB=AD,∠BAC=∠DAC,AC=AC;
∴ △ABC≌△ADC(SAS).
理由是:
1.已知:如图,AD∥BC,AD=CB.求证:△ADC≌△CBA
D
C
1
A
B
2
B
1
2
2.已知:如图5:AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
3.如图,AC=BD,∠CAB=∠DBA,你能判断BC=AD吗?说明理由。
A
B
C
D
判定方法1
两边及其夹角分别相等的两个三角形全等.
这个判定方法通常简写成“边角边”或“SAS”.
作 业
P16习题1.2 T1、2.
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
旧知回顾
04
例题精讲
1.通过实验探究得到全等三角形的判定定理1:两边及其夹角分别相等的两个三角形全等.
2.会用判定定理1解决相关的证明与计算问题.
1.什么叫做全等形,全等形有什么特征?
2.什么叫做全等三角形,全等三角形对应边和对应角有什么特点?
1.有一对元素相等
探究:需要几对元素相等,可得两个三角形全等
只有一组角或一组边对应相等时,得不到两三角形全等.
2.有两对元素相等
有两对元素对应相等时,也得不到两三角形全等.
(1) 两对角
(2) 两对边
(3) 一角一边
3.有三对元素相等
两个三角形有两条边和一个角分别对应相等时有几种情况呢?
边-角-边
边-边-角
这两种情况都能判定两个三角形全等吗?
实验与探究1
边-角-边
B
A
C
用符号语言表达为:
在△ABC与△ A′B′C′中:
AB=A′B′,∠B=∠B′,BC= B′C′
∴△ABC≌△ A′B′C′(SAS)
A
B
C
A′
B′
C′
判定方法1 两边及其夹角分别相等的两个三角形全等.
这个判定方法通常简写成“边角边”或“SAS”.
提示:登录优教同步学习网,搜索动画演示:两个三角形全等的判定方法(SAS)
如图,下列三角形中,哪两个三角形是全等三角形?
4
5
30。
①
40。
6
4
②
40。
6
4
③
4
5
40。
④
D
E
A
B
C
F
想一想
实验与探究2
边-边-角
例1 如图1-10,已知AB=AD,
∠BAC=∠DAC,△ABC与△ADC全等吗?说明你的理由.
解: △ABC与△ADC全等.理由是:
在△ABC与△ADC中,
∵ AB=AD,∠BAC=∠DAC,AC=AC;
∴ △ABC≌△ADC(SAS).
理由是:
1.已知:如图,AD∥BC,AD=CB.求证:△ADC≌△CBA
D
C
1
A
B
2
B
1
2
2.已知:如图5:AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
3.如图,AC=BD,∠CAB=∠DBA,你能判断BC=AD吗?说明理由。
A
B
C
D
判定方法1
两边及其夹角分别相等的两个三角形全等.
这个判定方法通常简写成“边角边”或“SAS”.
作 业
P16习题1.2 T1、2.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
